数学解题教学要“三悟”

福建省古田县第一中学 (352200) 兰诗全

解题教学是数学教学的重要组成部分，师生要在解题思维互动生成中有感悟、品悟、领悟．感悟出知识的来龙去脉，品悟出解题中的具体方法和规律，领悟出其中蕴涵的数学本质与思想，在悟中让课堂充满思辨，在悟中让知识得以延伸，在悟中揭示问题本质让数学思想得到升华．通过解题反思，要能悟出智慧，悟出真理，这是解题教学的核心与关键．

1 悟错因

在数学教学过程中，经常会发现学生在解题中犯下各种各样的错误，事后师生都在努力纠错，教师讲得累，学生纠得苦，可是效果却不明显，到下次解题时又重复“昨天的故事”．为什么呢？一大关键是学生没有深层次地找到错误的真正原因，没有一个与错误作“斗争”的过程，对错误原因没有追根溯源，没有揭示问题的本质，一错再错成必然．

以上是学生在课堂上的两种不同解法，两种解法似乎都很有“道理”，但至少有一错，到底错在哪里？教学契机大好，这是一个很难得的教学资源，要深挖对与错的原因，努力做好纠错教学，悟出错因．

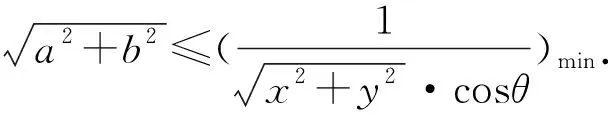
教师善于抓住纠错时机，通过示错—纠错—悟错的教学过程，启迪学生思维，让学生误中思，思中悟，误中求悟，让学生真正明白错误的原因，有效防止一错再错．

2 悟方法

学生解题再多，若不总结规律方法，仍不能举一反三，达不到教学效果．“不思不悟、小思小悟、大思大悟”有思才能有所悟，以思生悟．教学中要力求学生多思考懂规律悟方法，才能以少胜多，高效解题教学．

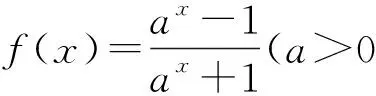
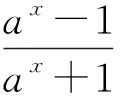
3 悟本质

本质是删繁就简，探幽索隐后的抽象提炼，是比规律更深刻更内在的东西．发现本质是接近真理的最有效方式，发现本质是数学解题的最高境界．

一本教学参考书有以下一例并作了错因分析.

例3 在钝角三角形ABC中，a=1,b=2,c=t,且C是最大角，求实数t的取值范围.

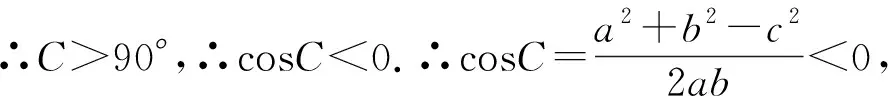
思考:以上错因分析击中要害了吗?是接受还是深挖本质？

若按照以上错因分析的说法,即用了余弦定理后,还要再考虑三边能否构成三角形.难道三边满足了余弦定理,还未必能构成三角形?作以下探索.

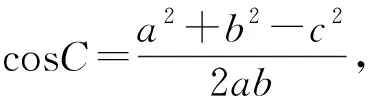
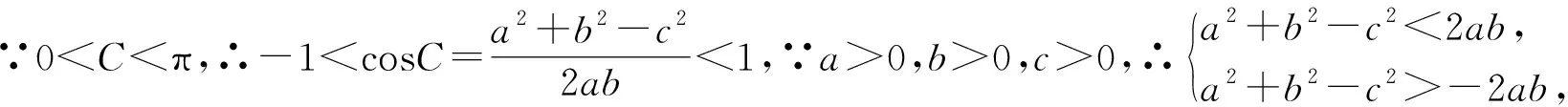
所以不难有结论:若三边满足余弦定理,则这三边一定能构成一个三角形.故参考书中的错因分析未能击中要害,未揭示问题的本质,易引起误解.那么,以上错解究竟错在哪里呢?关键是未将问题作等价转化.现提供以下正解.

这小小的改动,它可击中要害,是对问题的本质理解.数学解题一定要反思悟透,挖出问题的本质,这样才能达到真正理解真正掌握．

数学学习要解题，但不能陷入题海，不能让学生成为解题的机器．对做过的题目要进行反思总结，并站在一定的高度加以审视，从中发掘题目的精髓，看清问题的本质，对数学有思有悟，这样，学生才能从更高的观点，用更宽的视野，更理性的眼光，去思考解决数学问题，让数学课堂不断出新出奇出彩，让数学解题教学真实高效．