利用构造思想解导数综合题的五个意识

浙江省杭州外国语学校 (310023) 张传鹏

高中数学新课标中要求教师在教学中要提升学生的数学学科核心素养，即引导学生能够能从数学的角度看问题,有条理地进行理性思维、严密求证、逻辑推理和清晰准确地表达的意识与能力.学生在数学学习过程中进行感悟思想、经验积累，通过思考内化为自己的东西，所养成的自己独有的思考和表达问题的一种习惯，就是数学核心素养.本文结合导数章节的教学，谈如何利用构造思想去解导数综合题，在知识解决的同时，如何落实高中数学学科核心素养，从而实现了从关注知识本身到关注学生思维方式的转变，最终达到学科育人.

一、常规多次构造函数意识

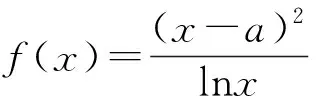
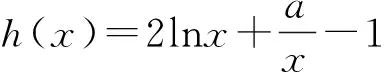
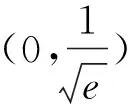
评注：导数是研究函数性质的一个重要工具，在解决不等式证明等问题时，通常需要构造函数，有时候甚至需要多次构造函数.要清楚多次构造函数的目的是什么，不要盲目的进行多次构造.

二、构造利用导数几何意义的意识

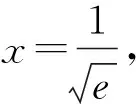
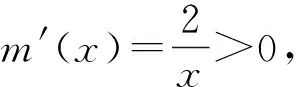
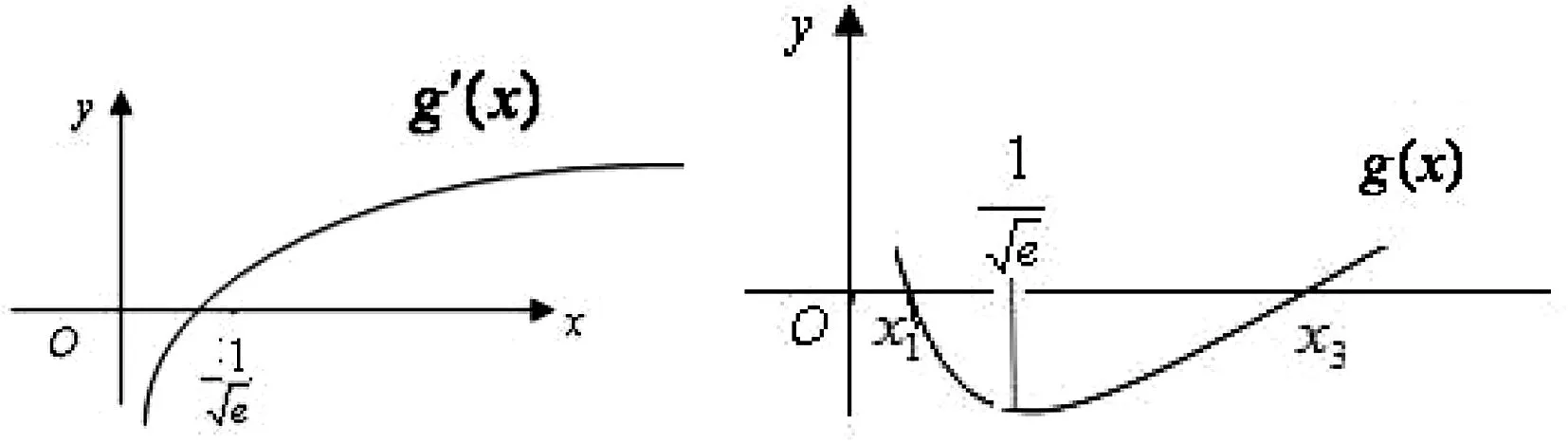
图1 图2

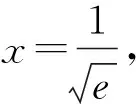
三、构造函数解决不等式证明问题的意识

例2 设函数f(x)=ln(1+x)，g(x)=xf′(x)，x≥0，其中f′(x)是f(x)的导函数．

(1)若f(x)≥ag(x)恒成立，求实数a的取值范围；

(2)设n∈N+，比较g(1)+g(2)+…+g(n)与n-f(n)的大小，并加以证明．

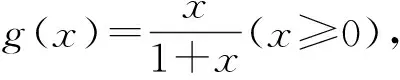
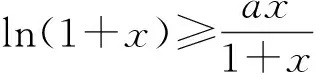
四、构造零点设而不求的意识

例3 已知函数f(x)=aex-1-lnx+lna，若不等式f(x)≥1恒成立，求实数a的范围.

评注：在一些涉及到指数函数、对数函数的问题时，若要求函数的极值点时需要解一些超越方程，但有时是无法解出这些方程的解，此时可以巧妙的借用方程的等价条件，采用设而不求的策略，使得问题得到解决.

五、逆向分析的构造意识

解决函数单调性问题时，有时需要借助构造新函数，结合函数的导数与函数单调性之间的关系来解决，那么怎样合理的构造新函数就是问题的关键.在解题过程学会如何进行分析与思考，如何从题目要解决的结论出发，通过逆向分析，结合题目已知条件，找到破解问题的思路.

例4 设x∈[0,π],y∈[0,1],试求函数f(x,y)=(2y-1)sinx+(1-y)sin[(1-y)x]的最小值.

解：首先，当x∈[0,π],y∈[0,1]时，f(x,y)=(2y-1)sinx+(1-y)sin(1-y)x

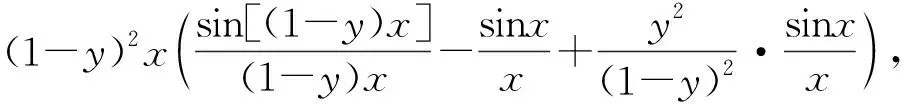
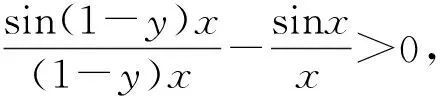
总之，在学习导数章节时，应关注以上五个意识.其中意识一：多次构造函数的意识，还是强调数学知识本身，因为导数知识最大的作用就是其在解决问题中的工具性，主要体现在利用导数研究函数的性质，前提条件就是构造恰当的函数.意识二：利用导数的几何意义的思想，导数值就是函数图像切线的斜率，如果再去研究切线斜率的单调性，即是去研究导函数的导数值的正负，其本质上就是研究函数的凹凸性.意识三：构造函数解决不等式问题的意识，则侧重于强调知识的应用性，利用导数求解出函数的最值，从中提炼出不等式并进行应用.意识四：构造零点设而不求的意识，是直面超越方程不能求解的问题，充分利用方程的等价条件解决问题.意识五：逆向分析的构造意识，是由题目要解决的结论出发，寻找结论与已知的联系.强调以导数知识为载体，对人的思维方式产生的影响，这就是我们所说的学科育人.可以发现，本文中强调的五个意识之间是相辅相成、层层递进的关系，其过程是从知识本身到知识的升华、知识的应用，最后达到学科育人的目的.