数学新情境问题教学的几点思考

江西省南丰一中 (344500) 肖志强

近年来，教育部相关部门对高考命题提出了不少具体要求，其中强调要“加强情境创设”.并认为“情境是高考评价体系的载体”，情境题能更好地考查学生的创新精神、实践能力及学生的核心素养，可见情境问题在高考中的重要地位.在数学高考考查方式中，问题情境和情境活动是通过文字与符号的形式进行的“以生考熟”问题转化的能力.为应对新高考中的情境背景要求，一线教师该采取什么应对的策略呢？

1.准确掌握基本概念，重视概念的生成过程

数学概念是构建数学理论大厦的基石，是导出数学定理和数学法则的逻辑基础，是数学学科的灵魂和精髓.只有掌握好概念，才能充分认识事物的本质，做出正确的判断与推理，才能够更好地解决一些由基本概念衍生出的新情境数学问题.概念教学过程，首先应重视教材中呈现的概念和方法，回顾概念的学习过程，重演定理的推导过程，从而加深对概念的理解并会对重点方法学会应用；其次应以问题为导向进行教学优化,要注意问题设计的有序性,层次性,广度性,深度性,在有效问题分析探索的基础上提高对概念的理解,强化“四基四能”,提高数学概念复习教学效果；在掌握和理解了一定的基础知识后，引导学生领悟深层知识(隐性知识)及其中的指数学思想和方法，使基础知识的掌握达到一个质的“飞跃”.

案例1 若一系列函数的解析式相同、值域相同，但其定义域不同，则称这些函数为“同族函数”，那么函数解析式为y=x2，值域为{1,4}的“同族函数”共有________________个．

解析：设函数y=x2的定义域为D，其值域为{1,4}，易知D的所有情形的个数，即是同族函数的个数.D的所有情形为{-1，2}，{-1，-2}，{1，2}，{1，-2}，{-1，1，2}，{-1，1，-2}，{-1，2，-2}，{1，2，-2}，{-1，1，2，-2}，共9个.

上述案例是新定义情境下的函数概念试题，本题给出了函数解析式相同、值域相同但定义域不同的“同族函数”新概念，其实质考查的是学生在新定义情境下对函数三要素的理解.

2.重视阅读方法引导，培养学生数学阅读能力

数学阅读能力是各种数学思维的基础和前提，其直接影响到学生数学学习过程中问题解决能力的形成和发展.目前学生数学阅读存在的问题是阅读能力低，概念模糊，无法理顺数据关系，不能顺利转化问题；生活常识匮乏，读不懂题，在新的情境中学生很难找出关键信息，关键信息的提炼不到位；教师没有给予学生阅读方法指导，忽视学生读题、审题、分析习惯的养成，等等.为此，教学中应重视阅读能力的训练.对概念的学习，要引导学生阅读，仔细辨析，找出概念的内涵和外延，达到理解要求.公式、定理、法则等教学要突出问题的背景、发生发展过程；解题教学过程中应引导学生认真读题，明确题意，学会搜集和处理信息的方法.

图1

3.加强问题情景题的训练，掌握问题解决的化归思想

“解题就是把要解的题转化为已经解过的题”，作为问题解决一般的化归思想，其实质就是“以生考熟”，就是用陌生的问题情境考查熟悉的知识和方法.

图2

案例3 (2015高考新课标Ⅰ理16)如图2，在平面四边形ABCD中，∠A=∠B=∠C=75°，BC=2,则AB的取值范围是________________.

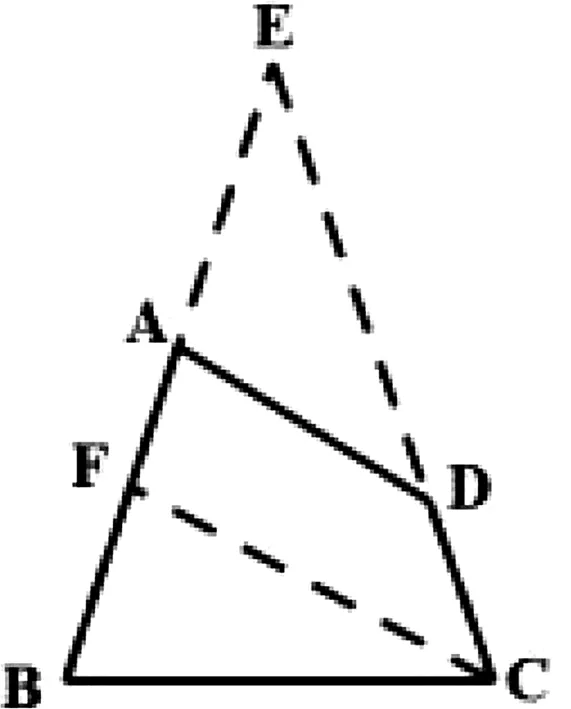
图3

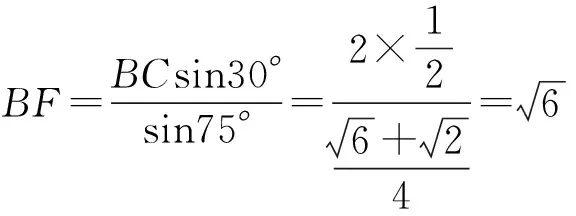
案例4 (2009高考重庆卷9)已知二面角α-l-β的大小为50°，P为空间中任意一点，则过点P且与平面α和平面β所成的角都是25°的直线的条数为( ).

A．2 B．3 C．4 D．5

解析：设平面α,β的法线分别为m,n，m与n所成的角是50°，过点P的直线与平面所成的角是25°，则与平面的法线所成的角是65°，问题即转化为：已知两直线m与n所成的角是50°，则过空间中一点P与m,n所成的角都是65°的直线有几条？易知选B.

案例5 如图4，在棱长为2的正方体ABCD-A1B1C1D1中，P是B1C的中点，Q,R分别在BC,BD上，则△PQR周长的最小值为________________．

图4 图5 图6

实际上，本题可转换成问题:如图5，一只蚂蚁从三棱锥P-BCD的顶点P出发,沿表面绕经棱BD和BC回到点P,最短路径长为________________.

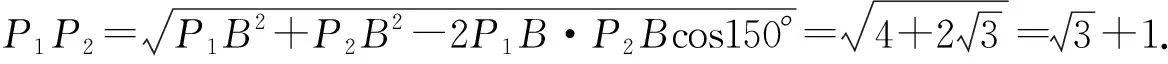
新情境的试题在近年高考中出现的频率很高，创新更明显，越加体现出对学生数学应用能力和数学阅读能力的要求，也体现了对数学学科素养的考查.我们教学中，应更强调牢牢把握数学教学的新课程理念，真正落实从“四基”“四能”到“三会”，再到“核心素养”这一主线，真正达到强化概念基础、培养数学阅读能力、掌握化归思想的目标.