平面与平面垂直性质定理推广及其应用

广东省广州市花都区秀全中学(510800)董大新

平面与平面垂直性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.

如图1 如果把“垂直于交线l”这个条件放宽为“平面α内直线a垂直于平面β内的直线b”,还会有线面垂直这个结论吗?答案是肯定的.

图1

推广若两个平面垂直,且一个平面内的一条直线垂直于另一个平面内的一条直线,则这两条直线至少有一条与其中一个平面垂直.

证明不失一般性,对平面β内直线b与交线l的位置分类考虑:若直线b与交线l重合,如图1,则为面面垂直性质定理情形,显然直线a⊥平面β;若b⊥l,如图2,同样为面面垂直性质定理情形,可知直线b⊥平面α;若直线b斜交交线l,如图3,在直线b上取一点G,在平面β上作直线GM⊥l,与交线l相交于点M,则GM⊥平面α,GM⊥a又∵a⊥b,b ∩GM=G,∴直线a⊥平面β.

图2

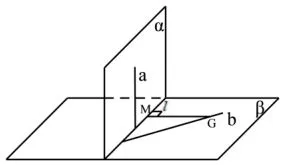
图3

综上所述,不论直线的位置情况如何,两条直线都有一条直线垂直其中一个平面.这个推广在面面垂直背景下可以很轻松地寻找出新的线面垂直!非常实用.

例1如图,已知AC⊥平面CDE,BD//AC,在ΔECD中,CE=CD,F为ED边的中点,BD=2AC

(1)求证:CF//面ABE;

(2)求证:面ABE⊥平面BDE:

分析:第(1)问很易得到,取BE的中点G,则故CF//AG且相等⇒CF// 面ABE

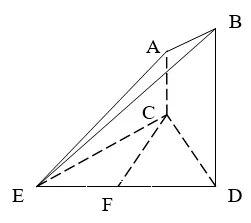
第(2)问要证面ABE⊥平面BDE,由上述推论可知,只需在这两个面内分别找到一条线相互垂直即可,由第(1)问可知四边形ACFG是矩形,因此AG⊥GF,又因为GF不可能垂直面ABE,可断定AG⊥面BDE,从G点是中点判断AE与AB必相等.整个推理过程明确简短

例2[2012·全国卷]如图4,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,AC=2,PA=2,E是PC上的一点,PE=2EC.

图4

(1)证明:PC⊥平面BED;

(2)设二面角A-PB-C为90°,求PD与平面PBC所成角的大小.

原解答:(1)证明:略

(2)在平面PAB内过点A作AG⊥PB,G为垂足.因为二面角A-PB-C为90°,所以平面PAB⊥平面PBC.又平面PAB∩平面PBC=PB,故AG⊥平面PBC,AG⊥BC.BC与平面PAB内两条相交直线PA,AG都垂直,故BC⊥平面PAB,于是BC⊥AB,所以底面ABCD为正方形,.

设D到平面PBC的距离为d.因为AD//BC,且AD /⊂平面PBC,BC ⊂平面PBC,故AD//平面PBC,A、D两点到平面PBC的距离相等,即设PD与平面PBC所成的角为α,则.所以PD与平面PBC所成的角为30°.

分析:问题(2)无论是用几何法还是用坐标法,都要通过条件“二面角A-PB-C为90°获取更具体的某些线的位置或长度关系”,参考答案一开始就是“在平面PAB内过点A作AG⊥PB”显得很突然,而且推理的最终目标是什么不清楚,经过较长的推导后才得出BC⊥平面PAB,但如果具有了本文推广的知识则是很必然:因为二面角A-PB-C为90°,所以平面PAB⊥平面PBC.接下来要去寻找分别属于两平面内相互垂直的两条线,从PA⊥底面ABCD非常容易得到了它们是:PA⊥BC,按推广马上可以判断要么PA⊥平面PBC,要么BC⊥平面PAB,由于PA斜交交线PB,根据推广证明中的第三种情况知一定有BC⊥平面PAB,“过点A作AG⊥PB”就是必然的了.

从上面两例可知,推广定理的应用主要在两个方面:一个是证明面面垂直,一个是从面面垂直推出线面垂直.思路都是一样:从面面垂直(已知或要证)的两平面内部分别寻找互相垂直的直线,再判断两线中的一条是斜交交线(绝大多数情况),那么另一条线必垂直对应的平面.

有了对面面垂直性质定理推广的理解与认识,在面面垂直的背景下可以快速发现线面垂直这一重要位置关系,思路非常清晰简洁,解决问题快捷,对图形位置关系的把握会更加直接准确,加强了空间想象能力.