电场作用下W/O乳化液中水颗粒的形变模拟与动力学分析

王楠楠，陈家庆，刘 帆，王晓东，安申法，栾智勇，张宝生，黄松涛

(1.北京石油化工学院 机械工程学院，北京 102617；2.华北电力大学 工程热物理研究中心，北京 102206；3.中国石化 胜利油田分公司石油工程技术研究院，山东 东营 257067)

在原油集输处理和炼制加工等环节，需要控制原油中的水含量，而在众多原油破乳脱水技术中，电场破乳技术的应用相对广泛[1]。为了提高电场破乳效率，确定合理的电场参数，有必要从微观尺度深入研究电场作用下油包水(W/O)型乳化液中分散相水颗粒的变形行为，研究方法主要分为微观实验和数值模拟两类。微观实验研究主要利用显微观测和高速摄像等手段，观察分散相水颗粒在电场作用下的运动、变形和破碎情况，但较难实现从水颗粒变形动力学和机理的角度进行分析考察。随着计算机数值模拟软、硬件技术的不断发展，其逐渐被应用于水颗粒在电场作用下的行为模拟。数值模拟过程可以灵活地改变模拟条件，以便揭示体系物性参数、电场参数的变化对水颗粒变形的影响规律。

2013年，西安交通大学危卫等[2]研究了电场作用下液滴的变形及力学行为，结果表明：均匀电场下液滴内部形成稳定的回转运动，不会发生宏观运动；由于库仑力作用，液滴不仅会发生变形，也会沿电场线方向运动。北京化工大学梁猛等[3]和哈尔滨理工大学陈庆国等[4]分别于2014年、2015年采用数值模拟方法考察了交流电场作用下分散相水颗粒的变形特征，结果均表明：增加电场强度、增大水颗粒直径和减小界面张力均有助于水颗粒变形，但当电场强度过大时水颗粒容易发生电分散现象。中国石油大学(华东)吕宇玲等[5]在2015年开展了电场和剪切场耦合作用下双液滴聚结过程的数值模拟，认为电场和剪切场协同作用下双液滴的行为可以分为不聚结、聚结和聚结后破裂3种类型；双场协同作用比单场作用下的双液滴聚结效率至少提高63%；毛细数、电毛细数及雷诺数在一定范围内的增大均能明显提高双液滴聚结效率。自2017年以来围绕液滴在电场作用下的变形行为开展了系列数值模拟[6-8]，首先模拟了电场频率、电场强度、液滴直径、界面张力和连续相黏度对半正弦波电场下液滴变形的影响，发现低频条件下液滴振荡变形频率与电场频率相同，水颗粒变形度随场强和液滴直径的增加而增大，随界面张力和连续相动力黏度的增加而减小；继而，研究了液滴极化变形的规律，发现增加电场强度和电场频率、减小液滴界面张力、增大液滴粒径等都有利于增大液滴极化变形幅度；在此基础上，对非均匀正弦交流电场中液滴在介电泳力下的迁移规律进行模拟，发现随着电压和粒径的增大以及油相黏度的减小，液滴向高场强区域的迁移速度增大随着频率的增大，液滴迁移速度先增大后减小，且在整个过程中液滴速度呈波动变化。2018年，北京石油化工学院尹永明等[9]研究了非均匀电场中分散相水颗粒的动力学行为，结果表明：非均匀电场导致水颗粒表面电荷密度分布不均，靠近电极端表面电荷密度和电场力最大；在一定范围内增大电压和水颗粒粒径，水颗粒变形量增大。2019年，华北电力大学He等[10]采用分子动力学模拟手段，研究了不同波形脉冲直流电场作用下带电液滴的电凝聚行为，结果表明：方波和正弦波具有相同的均方波场强，而三角波的均方波场强较小；当两个液滴合并成一个大液滴后，聚结液滴会发生周期性形变，与正弦波和三角波相比，方波下的液滴形变明显方波和正弦波具有几乎相同的临界场强，而三角形波临界场强更强。

总的来看，虽然上述研究分别从不同角度考察了电场作用下水颗粒的形变和迁移行为，但围绕多种电压波形对水颗粒变形程度的影响比较、是否存在最优电场参数、连续相物性参数对水颗粒变形影响的内因、分散相液滴变形的动力学特征等方面的研究较少。因此，笔者拟借助COMSOL MultipysicsTM软件，对电场作用下不同条件时水颗粒的变形规律进行数值模拟，考察电场强度、电压波形、电场频率、水颗粒半径和连续相黏度对水颗粒变形和变形度变化动力学的影响，以优化W/O乳化液电场下破乳的工艺条件。

1 有效数值模型的建立与验证

1.1 几何模型与边界条件

W/O型乳化液中水颗粒在电场作用下的数值模拟二维几何模型如图1所示。由图1可知，3-1和3-2为电极板，间距为6 mm。初始状态下水颗粒1的半径(r)为0.34 mm；在电场作用下，水颗粒1被拉伸，在某时刻的状态如水颗粒2所示。在该数值模拟二维几何模型中，水相和油相的相对介电常数分别设为1和3，其他参数按照系统默认值设置。

1—Water droplet before deformation,r=0.34 mm;2—Water droplet after deformation;3-1 and 3-2—Electrode plate图1 W/O型乳状液中水颗粒在电场(U)作用下变形模拟的二维模型Fig.1 Two dimensional models of water droplet deformation simulation in W/O emulsion under electric field (U)

1.2 控制方程

(1)描述电场控制的方程为麦克斯韦方程，如式(1)所示。

(1)

式中：ε0为真空介电常数，取值8.8542×10-12F/m；εr为相对介电常数，无量纲；U为电场电势，V。

(2)根据Navier-Stokes方程，用来描述层流两相流流体流动的控制方程如式(2)～式(3)所示。

(2)

(3)

此外，将水颗粒的变形度(C)定义为式(4)：

(4)

式中：a、b分别为水颗粒变形后的长径和短径，mm；变形度C无量纲。

1.3 网格无关性验证

本研究网格划分利用软件COMSOL MultipysicsTM采用“物理场控制网格”方式自动进行。为了消除网格尺寸对模拟结果的影响，在其他模拟条件(电场强度(E)为3 kV/cm，电场频率(f)为50 Hz，交流矩形波，连续相黏度(μc)为0.25 Pa·s)不变时，对比不同网格尺寸下的模拟结果。

利用4种不同网格尺寸划分的网格单元数分别为3272、4984、19896、77628。网格单元数为19896时的网格示意图如图2(a)所示，4种网格尺寸下水颗粒变形的模拟结果如图2(b)所示。从图2(b)可以看出：网格尺寸越小，水颗粒变形度越大；网格尺寸细化程度越高，水颗粒变形度曲线相差越小。因此，考虑模拟准确性、计算机计算强度和模拟时间，选用网格单元数为19896。

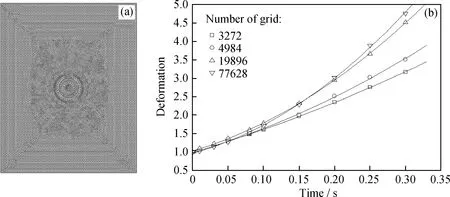
图2 网格划分和网格无关性验证Fig.2 Mesh generation and grid independence verification(a)Generation of mesh;(b)Verification of grid independenceConditions：E=3 kV/cm；f=50 Hz；μc=0.25 Pa·s；AC rectangular wave

1.4 模型验证

将实验结果与模拟结果对比来验证模型的准确性。实验条件与模拟条件一致，即：电场强度为3000 V/cm，电场频率为50 Hz，水颗粒半径为0.34 mm，电压波形为矩形，连续相黏度为0.25 Pa·s。显微观测系统的实验装置与实验步骤参见文献[11]，模拟验证结果如图3和表1所示。从图3和表1可以看出：不同时间下，实验与模拟过程中水颗粒变形情况类似，即随着时间的延长，水颗粒变形度不断增大；相同时间下，实验过程与模拟过程中水颗粒变形度相近，说明模拟模型的准确性较好。

图3 实验结果与模拟结果的对比与验证Fig.3 Comparison and verification of experimental results with simulated results(a)Simulated results；(b)Experimental resultsConditions：E=3 kV/cm；f=50 Hz；μc=0.25 Pa·s；r=0.34 mm；AC rectangular wave

表1 不同时间实验与模拟水颗粒变形度(C)Table 1 Water droplet deformations (C)of experimental and simulated results at different time

2 数值模拟分析

数值模拟的基本条件为：电场强度3000 V/cm，电场频率50 Hz，连续相黏度0.25 Pa·s，电压波形交流矩形波。在该条件下，考察单一因素变化对模拟结果的影响时，其他因素保持不变。

2.1 时间对水颗粒变形度的影响

不同时间下水颗粒变形度的模拟结果如图4所示。由图4可以发现，随着模拟时间的延长，水颗粒不断的被拉伸，水颗粒变形度变化显著。

图4 基本模拟条件时水颗粒在交流电场作用下的变形情况Fig.4 The deformation of water droplet in AC electric field under basic simulation conditionsSimulation conditions：E=3 kV/cm；f=50 Hz；μc=0.25 Pa·s；r=0.34 mm；AC rectangular wave

2.2 电场参数对水颗粒变形度的影响

2.2.1 电场强度

分别对乳化液施加0.5、1、2、3、4、5 kV/cm共6种不同的电场强度，考察电场强度变化对水颗粒变形度(C)的影响，结果如图5所示。由图5可知：C受电场强度的影响明显；当电场强度在 0.5～4 kV/cm时，相同时间内电场强度越大，C越大；而当场强增大到5 kV/cm时，水颗粒在短时间内开始发生分裂，在0.17 s时彻底分裂成5个小的水颗粒(图5(b))，说明电场强度存在上限值，达到上限值后不仅不利于水颗粒聚结，反而会发生“电分散”现象。这与基于大量工程实践的认知相符。

图5 电场强度对水颗粒变形度(C)的影响Fig.5 Effect of electric field strength on deformation (C)(a)Variation kinetic of deformation of water droplet at different electric field strength；(b)The deformation of water droplet at 5 kV/cmSimulation conditions：f=50 Hz；μc=0.25 Pa·s；r=0.34 mm；AC rectangular wave

水颗粒在电场中所受的电场力大小与电场强度和水颗粒极化电荷量成正比[4]，如式(5)所示。

F=E·q

(5)

式中：F为水颗粒受到的电场力，N；E为电场强度，V/m；q为水滴上的极化电荷量，C。因此，在水颗粒不发生“电分散”前提下，E越大，水颗粒所受F越大，则其变形度C越大。

2.2.2 电压波形

电压波形选择交流矩形波、交流锯齿波、直流脉冲波、交流三角波和交流正弦波共5种代表性波形。在5种电压波形下进行单因素变化模拟研究，结果如图6(a)所示。从图6(a)可以看出：水颗粒在交流锯齿波下的变形效果与交流三角波下的相似，且C最小；在直流脉冲波和交流正弦波下的变形效果相似；而在交流矩形波下变形度C最大，0.3 s时达到4.3，明显大于其他4种波形。

以Em和Ee分别代表有效电场强度的最小值和最大值，电场可按电场强度分为3个区：无效电压区(EEe)，如图6(b)所示。由图6(b)可知，5种电压波形下水颗粒变形度C随着时间变化的差异，主要是由5种波形在有效电压区中持续时间不同及电压的变化趋势不同所导致。此研究中，水颗粒在5种电压波形下均未发生破裂，说明5种电压波形所施加的电场强度均未处于电分散区。对比5种电压波形在有效电压区中的持续时间，可以发现交流矩形波在一个周期内工作的所有时间均处于有效电压区，其他4种波形均有一定时间处于无效电压区。而在无效电压区，由于电压过小，无法使水颗粒变形。另外，交流矩形波的工作电压在所有时间内均处于最大电压状态；而交流锯齿波、交流三角波和交流正弦波的电压均在不断发生周期性变化，其电压一直小于最大电压；直流脉冲波虽然在工作时一直处于最大电压状态，但有50%的时间电压为零。故在相同时间内，以上4种波形的电压对水颗粒做的功均小于交流矩形波电压的，因而其作用下水颗粒的变形度小于交流矩形波作用的。该结果与文献[12]的实验结果相符。

图6 电场波形对水颗粒变形度(C)的影响Fig.6 Effect of electric field waveform on deformation (C)(a)Variation kinetic of water droplet deformation；(b)The voltage amplitude variation of five voltage waveformsSimulation conditions：E=3 kV/cm；f=50 Hz；μc=0.25 Pa·s；r=0.34 mm

2.2.3 电场频率

分别在较低频率范围(10～200 Hz)和较高频率范围(900～5000 Hz)考察不同电场频率对水颗粒变形度C的影响，模拟结果如图7所示。从图7(a)可以看出，在10～200 Hz范围内，不同电场频率下水颗粒变形度C随时间的变化趋势总体上一致，且C较小，说明较低电场频率对水颗粒变形度C的影响可以忽略。这是因为电场频率没有达到水颗粒的固有振动频率，导致电场影响不明显[13]。当电场频率在较高频率范围时，电场频率变化对C的影响先增大再减小，在电场频率2000 Hz时水颗粒变形度最大(图7(b))。

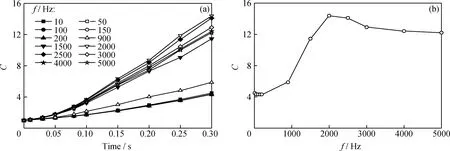
图7 电场频率对水颗粒变形度(C)的影响Fig.7 Effect of electric field frequency on water droplet deformation (C)(a)Variation kinetic of water droplet deformation at different electric frequency；(b)Effect of frequency on water droplet deformation at 0.30 sSimulation conditions：E=3 kV/cm；μc=0.25 Pa·s；r=0.34 mm；AC rectangular wave

2.3 乳化液特性参数对水颗粒变形度的影响

2.3.1 水颗粒半径

考察水颗粒不同粒径在交变电场中变形度的变化情况，模拟结果如图8所示。从图8可以看出，水颗粒粒径变化对其自身变形度有明显影响，随着水颗粒半径的增大，其变形度也是越来越大。这主要是水颗粒表面张力受半径的影响，水颗粒半径越大，表面张力越小，导致水颗粒本身抵抗变形能力越差[14]。

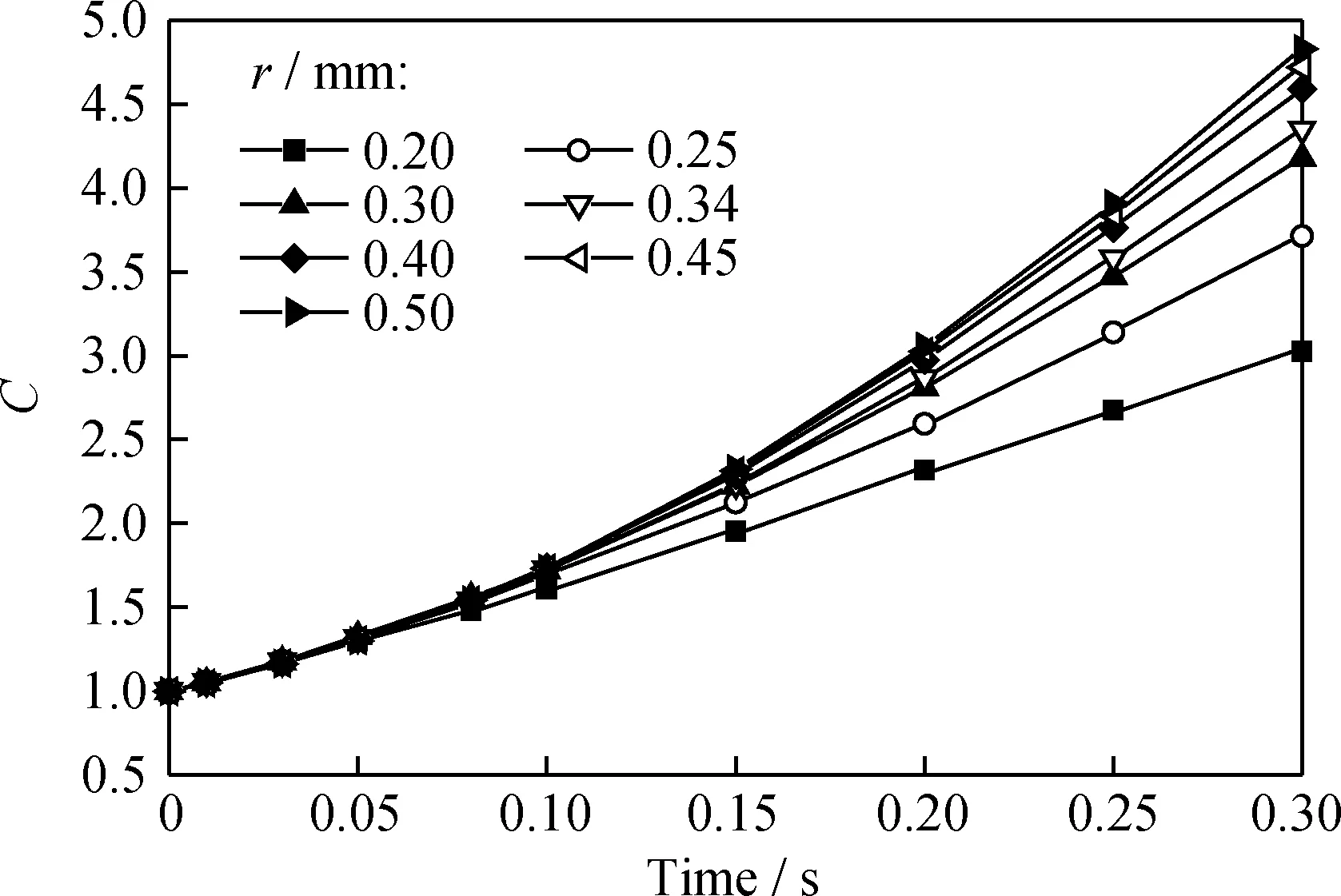
图8 水颗粒半径对水颗粒变形度(C)的影响Fig.8 Effect of water droplet radius on its deformation (C)Simulation conditions：E=3 kV/cm；f=50 Hz；μc=0.25 Pa·s；AC rectangular wave

2.3.2 连续相黏度

在其他模拟条件不变，连续相(油相)的黏度在0.18～0.50 Pa·s变化时[7,14]，水颗粒变形度的模拟结果如图9所示。从图9可以看出，随着连续相黏度的减小，水颗粒变形度C和变形速率增大，且变化较为均匀。这主要是因为连续相黏度降低时，水颗粒受到的连续相阻力不断减小，电场力的作用越来越明显[15]。

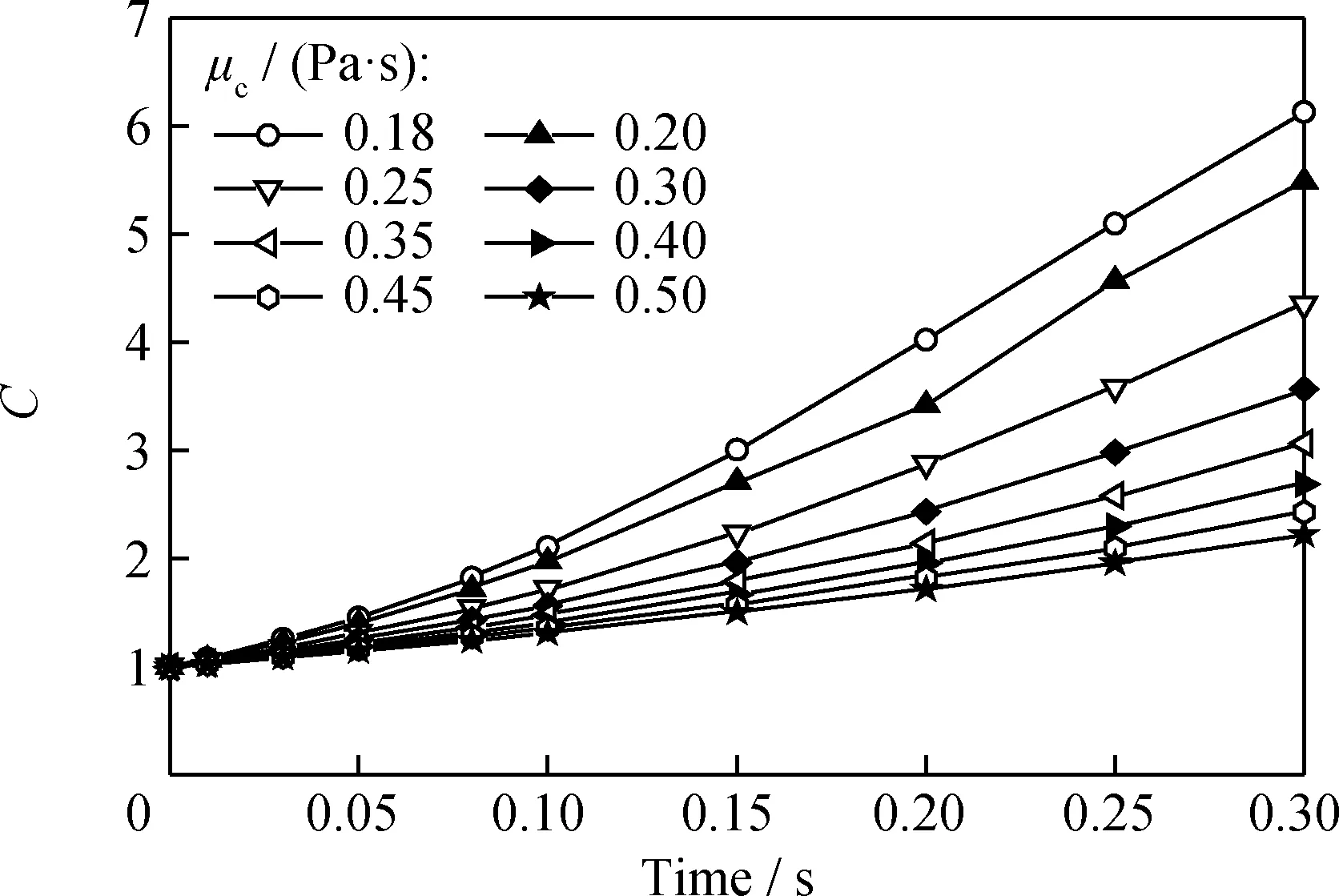
图9 连续相黏度对水颗粒变形度(C)的影响Fig.9 Effect of viscosity of continuous phase on water droplet deformation (C)Simulation conditions：E=3 kV/cm；f=50 Hz；r=0.34 mm；AC rectangular wave

2.4 水颗粒变形动力学分析

2.4.1 动力学模型

观察图5(a)、6(a)、7(a)、8和9中水颗粒变形度C的变化曲线可以发现，不同条件下，水颗粒变形度随时间的变化呈匀速或增速变化状态。各工艺条件下水颗粒变形度C随时间的变化速率(v)如式(6)所示。

(6)

式中：k为变形速率常数，min-1；n为变形级数。当n=0时，为零级动力学；n=1时，水颗粒变形度C的变化过程符合一级动力学；n=2时，符合二级动力学。n越大，说明v会随着C的增大而不断提高，即发生增速变形。由于水颗粒变形度越大越有利于水滴间的碰撞聚结，因此增速变形有利于缩短水颗粒间的碰撞聚结时间。特别地，n=0时，v为恒定值，即水颗粒发生恒速变形。在n为0、1、2时，分别对式(6)积分，得式(7)～(9)。

C-C0=k0·t(n=0)

(7)

(8)

(9)

式(7)～(9)中：C0为水颗粒初始变形度，即C0=1；k0、k1、k2分别为零级动力学、一级动力学和二级动力学的速率常数，单位均为min-1。

2.4.2 不同电场参数下水颗粒变形度的动力学拟合

对图5(a)、6(a)、7(a)中的数据分别进行零级、一级和二级动力学分析，得到不同电场强度、电压波形、电场频率下水颗粒变形度C的变化动力学如表2所示，其中R02、R12、R22分别为零级、一级和二级动力学时的相关系数。

表2 不同电场参数下水颗粒变形度C的变化动力学Table 2 The kinetics of water droplet deformation (C)under different electric-field parameters

由表2可以发现：当电场强度为0.5～2 kV/cm时，C随时间的变化数据拟合结果和零级动力学方程最符(R02值更大)，即水颗粒发生恒速变形；随着电场强度的不断增大(3～4 kV/cm)，C随时间的变化更符合一级动力学(R12值更大)，即水颗粒开始发生增速变形；当电压波形为交流矩形波时，C随时间的变化符合一级动力学；而电压波形为其他波形时，C随时间的变化符合零级动力学；而在整个电场频率变化范围内，C的变化均符合一级动力学。

2.4.3 乳化液体系不同特性参数下水颗粒变形度的动力学拟合

对图8～图9中的曲线数据分别进行零级、一级和二级动力学分析，得到不同乳化液体系特性参数下水颗粒变形度C随时间变化的动力学，结果如表3所示。

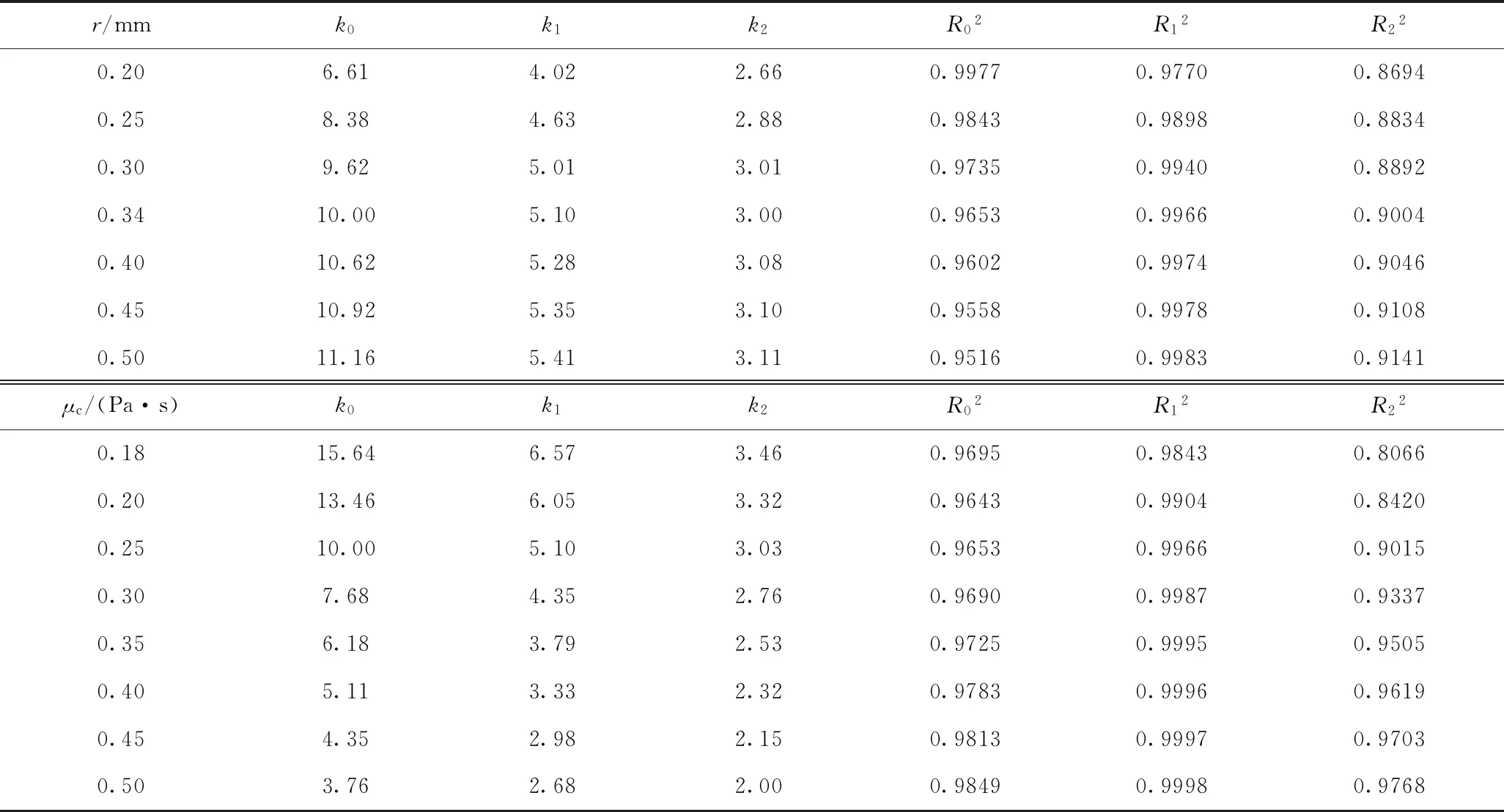
表3 乳化液体系不同特性参数下水颗粒变形度(C)的变化动力学Table 3 The kinetics of water droplet deformation (C)under different characteristic parameters of emulsion

由表3可以发现：当水颗粒半径为0.20 mm时，C随时间的变化符合零级动力学；当水颗粒半径增至0.25 mm时，C随时间的变化开始转向一级动力学；而且，在水颗粒半径在0.25～0.5 mm时，连续相黏度的变化(0.18～0.50 Pa·s)并不影响C随时间变化的动力学，一直符合一级动力学，即持续发生增速变形。

2.4.4 基于动力学分析优化电场破乳工艺

图10给出了不同因素影响水颗粒变形度C随时间变化动力学的分析结果。从图10可以发现，对C随时间变化动力学影响的因素主要有电场属性(电场强度、电压波形和电场频率)、水颗粒半径和连续相黏度。当电场强度为3～4 kV/cm，电压波形为交流矩形波，水颗粒半径为0.25～0.5 mm时，水颗粒变形度C随时间的变化符合一级动力学，即水颗粒发生增速变形。这有助于减少水滴之间的碰撞聚结时间，进而缩短W/O型乳化液的破乳时间。

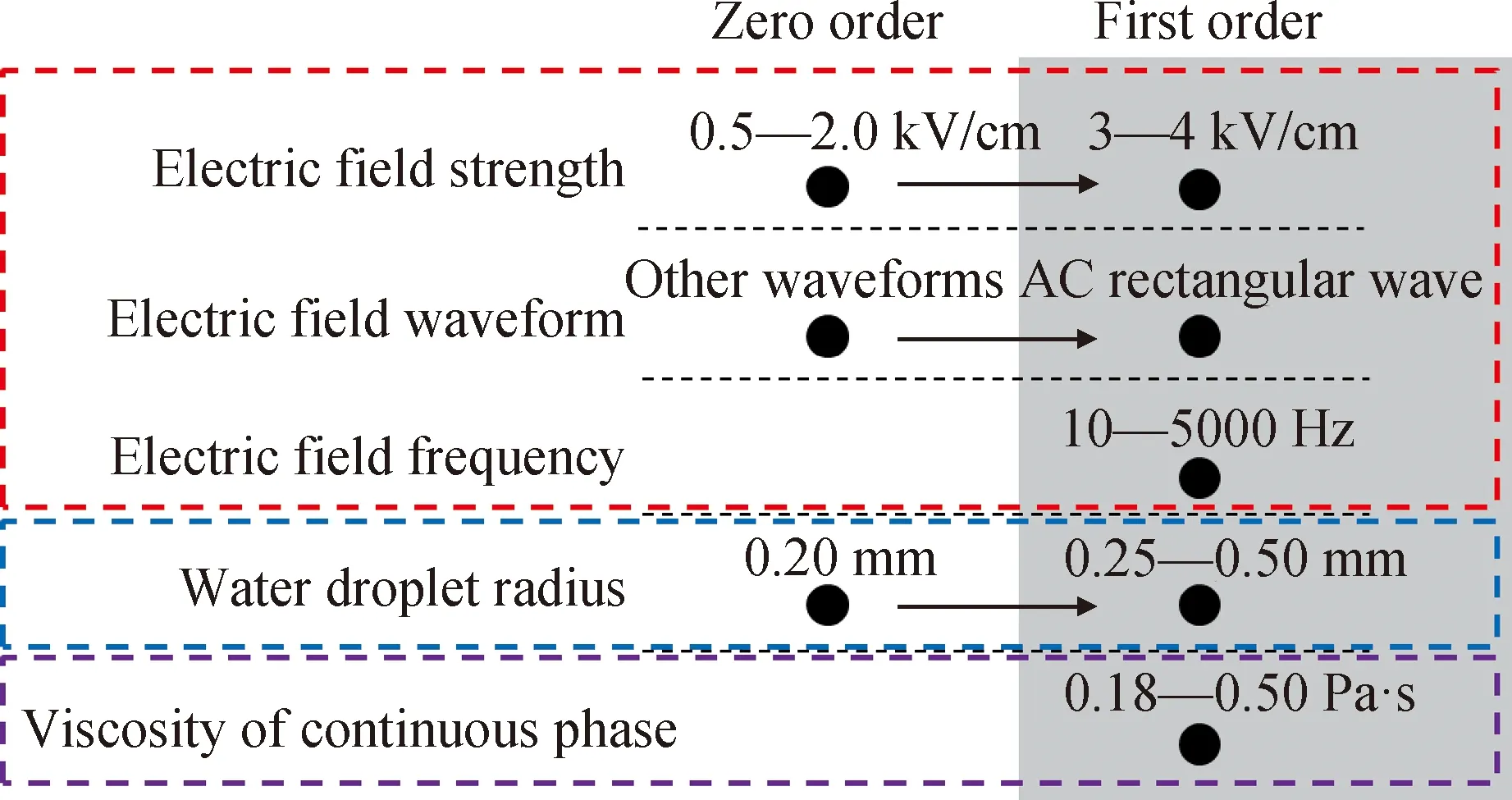
图10 不同影响因素变化时，水颗粒变形度(C)的变化动力学转化示意图Fig.10 Schematic diagram of kinetics of deformation (C) under different influence factors

3 结 论

运用数值模拟方法对低频电场作用下单水颗粒的变形行为进行研究，结果表明：

(1)在相同时间时，水颗粒变形度(C)随电场强度的增加而增大；但电场强度过大，水颗粒会发生“电分散”现象。电压波形对水颗粒变形度的影响很大；电压波形为交流矩形波时，电场处于有效电压区的时间最长，工作电压最大，C最明显。电场频率在10～200 Hz范围内对C影响不明显；随着频率的增大，电场频率的影响逐渐明显，最优电场频率为2000 Hz。

(2)随着水颗粒半径的增大，水颗粒表面张力有所减小，C不断增大；随着连续相黏度的减小，水颗粒受到的连续相阻力不断减小，C不断增大。

(3)影响C随时间变化动力学的因素主要有电场属性(电场强度、电压波形和电场频率)、水颗粒半径和连续相黏度。当电场强度为3～4 kV/cm、电压波形为交流矩形波、水颗粒半径为0.25～0.50 mm时，C随时间变化动力学符合一级动力学，水滴发生增速变形，可缩短W/O乳化液的破乳时间。