基于标准正态化的二十层回归分析法

黄玉平 何以建

前言

如何通过对学业成绩的分析来反映学校的管理水平和教师的业务表现，去除考试命题，阅卷，学生临场表现，班级差异，学生基础等干扰因素，形成公平合理的评价标准，一直是教育管理部门关注的技术问题。

本文给出的研究成果：基于正态化标准分的二十层回归分析方法，有效地解决了评估学校和教师教学成绩的标准问题。

一、现状分析

（一）均分排位变化分析法

此方法适用于相同基础的各地市之间的终结性比较，不论各地市的教育起点如何，直接用测试结果的均分进行排名，名次高低代表各地市教育水平的高低。例如，2017年，A市某项测试的均分位列全省第一，因此代表着A市2017年在某项的教育水平全省第一。这种分析法优点是：容易理解，容易计算，缺点是：很粗糙，不科学，反应慢，只反映结果，不反映进步程度。

（二）均分对比分析法

将同一个群体同一个科目两次考试的均分进行直接对比，由于可能受到两次考试难度不同，导致均分差异过大，另外标准差不同，也会使均分直接对比受到较大的影响，从而影响比较的效果。

用回归分析来处理两次考试的成绩，是一个值得尝试的方法。

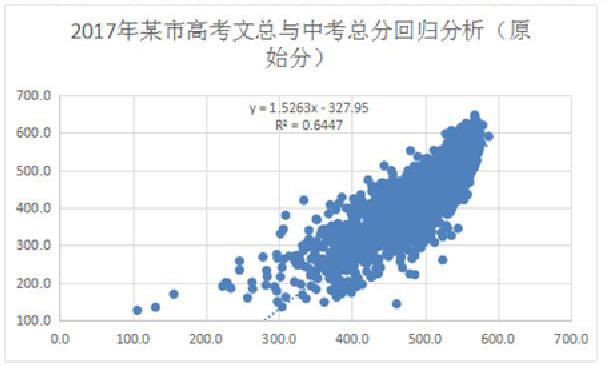
下图是某市2017届文科毕业生高考总分与中考总分的回归分析，具有较高的相关性，其线性相关的判定指数为0.644，毕竟经过了三年时间，中间已经有太多的因素对成绩产生影响。

这种方法的判定指数不到七成，还有三成多不能解释的因素，误差太大，还不适合直接用于分析学校和教师的教育质量。

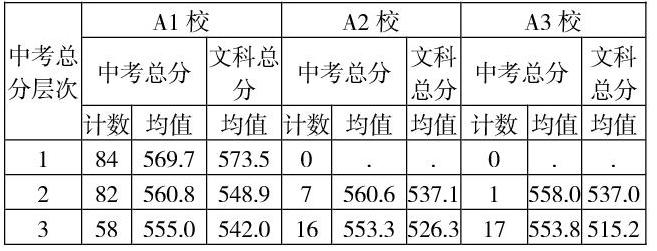
如果将第一次考试均分相同的一批学生的第二次考试成绩进行比较，可以横向比较出进步还是退步的学校。这种方法提供了横向比较的参照物，说服力大大地增强了。

在上表中，以中考总分第4层次为例，三个学校中考总分均分相差不到1分，高考文科总分差距最高为5分，能比较出高低。

经过一段时间的使用，发现这种方法的五个问题：第一，某些学校独占了某个均分层次，没有横向对比的学校，因此无法评价，例如上表中中考总分第一层次，只有A1校有学生，无法反映成绩的相对高低;第二，无法反映这个均分层次是否整体偏好或偏差，无法与其它层次进行比较，使评价有可能产生偏差;第三，一个学校均分各层次之间的比较结果能否相加，缺乏依据;第四，相同层次的各学校的中考总分均分不相同，直接看文科总分不够科学;第五，不直观，不能直接看出结果，效率低。

（三）简单标准分对比分析法

简单标准分的处理：通过利用与均分的差距比上标准差得到的Z分数，再进行线性变换（100Z+500），得到平均分为500，标准差为100的简单标准分。通过变换，有效地消除了均分和标准差不同的影响。

简单标准分的使用，可以使同一次考试不同科目之间，同一科目不同考试之间都可以进行比较，准确性有了较大的提高。

这种方法的问题在于：由于试题命制目的不同，两次考试的区分度也不同，观察散点图可以看出，两者之间的关系与二次曲线接近，如果直接比较，仍存在一定误差，影响评价的精确性。

如果采用回归分析，理论上可以找到期望函数，从而得到比较基准。但是多次试验的结果发现两个问题：第一，這种二次回归误差很大，不容易解释原因;第二，计算上没有线性回归方便。

（四）正态化标准分对比分析法

将考试成绩转化为正态化标准分，是一种巨大的进步，它能较好地将不同的考试造成的偏态经过转换，变形为正态分布，从而较好地消除不同考试区分部位与区分能力的不同。目前国际上公认的标准正态化处理共有五种算法，其中rankit算法在SPSS软件中自带，因此为实际使用提供了可行性。

将两次成绩转转换为正态化标准分以后，直接进行比较的误差还是不小的。

如果对全体学生两次正态化标准分的直接进行回归分析，回归效率提高了，但是残差还是不小。原因是：特别优秀的班级和特别弱的班级对学生成绩的影响体现出来了。

下图是某市2017年届文科毕业生文科总分标准分（正态化）与中考总分标准分（正态化）之间的线性回归分析，判定指数是0.706，从散点图上观察，一些数据偏离回归直线较多，受到学生个体与班级的干扰很大，不适合直接用于评价各校和各班的教育质量。

二、解决方案

珠海市教育研究院高中教育研究室经过多年研究，不断改进，于2012年正式定型，形成了目前的“基于标准正态化的二十层回归分析法”。

要真实反映教育的质量，须要进行前后的对比，不能只看目前的现状;

两次考试由于命题等因素的影响，区分度不同，导致原始成绩反映学生真实水平的程度不同，须进行标准化处理。如果对两次考试只是采用简单的标准化处理，虽然解决了两次考试的标准差不同问题，但是没有解决两次考试对于不同层次学生能力的区分度不同问题，例如水平性考试关注的是学生能否及格，对于学生是否优秀并不关注，因此试题更多的是基础型，多数学生能够获得较高的成绩，但是少数基础比较弱的学生，则成绩较弱，整体成绩呈现为负偏态（均分低于中位数）;而能力型考试关注的是学生是否具有较高的核心素养和学科能力，对思维和综合能力考查的试题较多，考试的结果是多数学生考分不能及格，而能力较强的学生能够突出表现，整体成绩呈现为正偏态（均分高于中位数），两次考试简单标准分明显不是线性相关关系。

由于都是线性变换，最后很有可能两次考试的标准分之间存在非线性相关，例如二次相关等，容易产生较大的误差，也不能进行分班分层的计算。经过反复试验和思考，现采用标准正态化处理，采用国际通用的rankit算法，对两次考试成绩进行标准正态化转换，解决了两次考试考查侧重点不同和区分度不同带来的困扰。

对两次考试成绩的正态化标准分进行相关性分析，发现相关性大大提高，对所有学生的两次正态化标准分进行线性回归分析，得到的判定指数达到了0.7。

每一个学校或班级，经过一段时间的教学，都容易产生分化，最低分与最高分之间差距巨大。用均分为代表一个学校或班级成绩，目的是反映群体的集中趋势，由于群体内各数据权重相同，均分很容易受到较特殊数据的影响，导致发生偏离，从而使分析效果下降。

在实践的过程中发现，各学校对基础非常敏感，不同基础的学校之间的比较数据，除非发生了反转，否则说服力不强。

同一批对象同一个科目两次考试之间的成绩存在非常明显的相关关系，采用标准正态化转换之后，发现这种相关关系进一步提高。

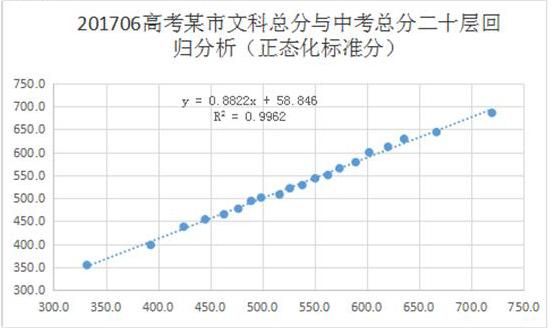
如果以学校均分为对象，进行两次考试的正态化标准分进行回归分析，获得如下的结果：两次成绩成线性相关，判定指数为0.95。学校内部班级的差异已经被消减，反映出在学校差异较小的情况下，两次考试的正态化标准分之间呈现高度线性相关。

以学校为对象的正态化标准的回归分析中，由于各校人数差异较大，使得较小的学校数据权重较大，影响回归结论。

通过对数据的观察，我们发现：学校之间表现差异非常大，班级之间的差异也非常大，如果用一个均分表达一个学校的成绩，其中受到这些差异因素的干扰太多，从而较大地影响了两次考试之间的回归分析效果。

如果将全市基础相近的学生作为一个群体，分析它们两考正态化标准分的均分之间的相关关系，能够具体有以下优点：第一，均分代表性增加;第二，各层次群体权重相近;第三，每个层次包括多所学校，能较好地消除学校差异对回归结果的影响，使回归分析结果更准确;第四，采用正态化标准分，有效地减小不同考试命题造成的差异性。

下表是某市2017年高考文科总分与中考总分二十层回归分析的结果：

三、操作步骤

（一）对齐

两次考试，人群是不完全相同的，做质量分析只能针对两次考试都参加的学生，因此将两个表格对齐，是第一个步骤。中考和高考的成绩表都有身份证号字段，用它做为连接两个表格的共同字段，只有身份证号相同的数据，才能保留下来。采用数据库的处理方法，能较快地对齐两个表格。为了今后复查，保留原始表格。

（二）合并

将两个对齐的表格合并成为同一张表，须将两个表格中相同的字段保留，例如：学校，身份证号，姓名等。同时，要将两张表中，两次考试的所有成绩都保留下来，重复的字段名，如语文、英语等，须分别改为中考语文、中考英语和高考语文、高考英语或类似的字段。

合并的表格，将首先按考试类别进行分类和排序，即文科和理科两类。学生类别中，只留下文科和理科两类，其它类如音乐、美术和体育等，都不进行集中处理，直接从表格删除。

合并这个环节的人工操作是不可少的。

（三）二十层分组

不同的分层，如果各层之间差距不是特别大，不影响统计结果。

将合并后文理合在一起的表格，按中考总分的高低排序，等量分为二十层，因有同分数学生，保持每层数量尽量相近，优先高分组。增加一个字段：二十层。给每个学生标注层次号：1，2，…，20。

（四）标准正态化

将分出二十层的表格，按文科和理科分为两张表，分别取名为：20XX年高考中考合并分层文（理）科表。

对中考五个科目和高考四个单科进行标准正态化处理，并分别增加相应字段。

将两考的单科标准分分别合并后，再根据rankit算法，对中考总分和高考的文科总分（理科总分）进行标准正态化处理，增加字段：中考总分标准分，文科总分标准分（理科总分标准分）。

（五）回归分析

下面以文科总分为例，说明回归分析的方法：

按二十层，分别计算各层的文科总分标准分的平均分和中考总分标准分的平均分;

将二十组数据进行回归分析，以中考总分标准分为横坐标，文科总分标准分为纵坐标，求出回归方程和判定指数，并标出来（如 ）;

将每个学生的中考总分标准分代入回归方程的横坐标，计算出每个学生文科总分标准分的期望值;

将每个学生的文科总分标准分减去它的期望值，得到比较值，即残差;

分别计算每个学校每个层次的比较值（残差）的平均值;

计算每个学校的比较值（残差）的平均值。残差的标准差为100左右，结合学校的人数，用标准误的方式，可以评判断学校进步或退步的幅度。

文科综合与中考总分进行回归分析。

理科综合与中考总分进行回归分析。

语文，数学（文科数学与理科数学），英语三科分别与中考相应科目回归分析。

四、应用举例

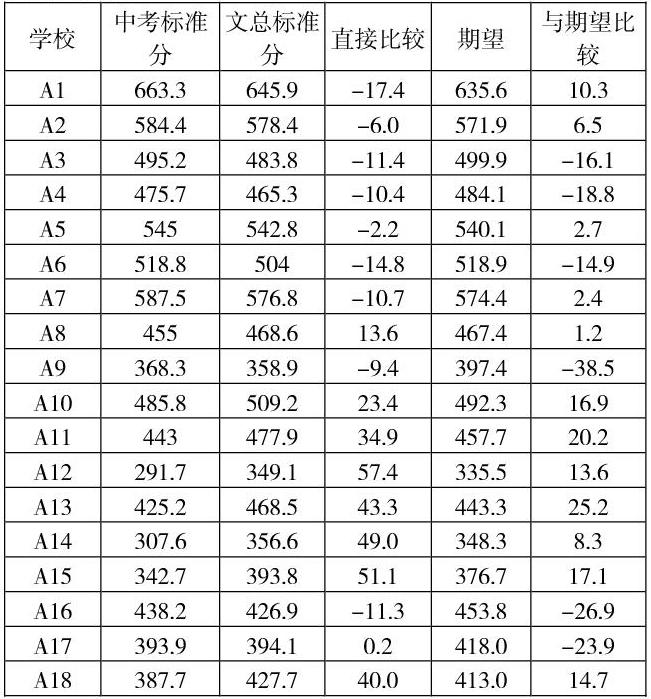
下面是2017年某市各校文科总分与中考总分二十层回归分析的结果（正态化标准分）：

各校进步或退步，在总计这里显示了，如A10学校，总计平均进步了22分，其中各批次都显示超过了期望值，因此表现非常突出;A3学校，总计平均退步了12分，其中八个层次中有六个层次都是负分，意味着比期望值低，这样与那些进步的学校差距就非常大了，说明整体水平不高。另外A1学校，总计平均进步了2分，但是其中第一个层次退步了8分，且这个层次是中考水平最高的，只有这一所学校有这一层次的学生，说明该校的优生培养较弱，还有提升空间。

表中对18所学校各个层次都进行了分析，针对性强。这个表只显示了各层次平均分与期望的比较，没有加上人数的影响，须结合各层次人数，才能掌握各校主要的得分或失分层次。

在上表中，可以发现，为总体进步贡献最大的学校是A18和A10两校，而A9则拖的后腿是最大的。其中A1校总体是进步，但是它的前两层，却是退步的，说明它对优秀生的培养，還有提高空间。

如果配合各科的分析，更能发现具体的问题。

上表中，A2校总分进步了14分，但是单科分析发现，主要贡献是文科英语，文科数学也有正贡献，而文科语文则负了6分，文科综合也负了3分，这样学科的情况清楚，有利于进一步的工作。类似的，A5校总分进步了13分，单科分析中发现，其中文科语文也负了3分。

继续分析A2校和A5校的文科语文的二十层，看看是哪些层次造成的影响。

在上表中，A2校的文科语文在十二个层次中七个层次是负分的，而且负分值较大，特别是第三层和第四层及第六层，差距较大。说明多数学生的语文学习存在问题。

A5校的语文出现负分的层次是第六层，第十层，第十一层，第二层，第十五层，主要是中下学生存在退步现象，有可能是教学中对基础的问题关注不够或解决不彻底。

五、结束语

采用本文办法，实现了增值评价。这种方法，可以将每个学校、每个班级的每个层面的教学成果在这两次考试成绩上定量地测量出来。其中远高于期望值的学校和班级，可能有与众不同的教育方法，值得特别关注，其中符合党和国家教育方向，符合学生的终身发展需要，符合学生实际情况的教育措施，应该及时总结和推广;对于其中远低于期望值的学校和班级，可能存在学校管理上的松懈和粗糙，校风不正，师德不良，教师不敬业，专业水平不高等诸多问题，须问责谈话，认真整改，切实找出问题，改正教风，端正态度。作为行政管理部门，应思考如何针对这些学校的问题，改进培训和支教的方式方法，帮助这类学校逐步改进工作方法，不断取得进步。

参考文献：

[1]刘娟，高振华，卢志舟，马春环，李鹏. 增值评价在学校效能评价中的应用【J】.教育测量与评价，2015（10）：48-52.

[2]万兵涛，许志勇，汪晓银. 教学质量增值评价中数学模型的选择与应用【J】.考试研究，2019（1）：98-104.