光子莫尔晶格的研究进展
2021-09-03傅其栋李雨芮叶芳伟
王 鹏,傅其栋,李雨芮,叶芳伟
(上海交通大学物理与天文学院,上海 200240)
1 引 言
莫尔晶格是指两个相同或者相似周期结构(称子晶格)重叠形成的复合结构。由于两个子晶格晶格常数的差异或者叠加时两个子晶格之间存在转角,该复合结构会在原来子晶格周期的基础上,产生一套长周期图样,即所谓莫尔条纹。在生活中,莫尔条纹并不罕见,比如:将两把梳子重叠即可形成莫尔条纹,两面纱窗重叠处会产生莫尔条纹,电风扇的前后网罩在视野中重叠也能产生莫尔条纹。当人们用手机拍摄电脑屏幕时,经常会看到彩色的莫尔条纹,摄影爱好者在拍摄衣织物时也会发现在照片上出现恼人的莫尔条纹[1]。鉴于莫尔条纹的长周期特点,莫尔条纹在艺术设计、纺织业、建筑学、图像处理、测量学和干涉仪等方面都有一些独特的应用,但这些应用基本上都是基于莫尔条纹的几何特点,对于莫尔条纹或莫尔晶格物理性质的研究并不多见。
对莫尔晶格物理性质的研究主要起源于范德华尔斯(van der Waals,vdW)异质结结构[2-5]。vdW 异质结结构是指两层(或者多层)二维材料堆叠在一起形成的超晶格,层间通过范德华尔斯力相互耦合。受层间耦合的影响,vdW 异质结出现单层材料所不具有的光电响应特性[4-9]。进一步,如果将上层材料相对于下层材料转过一个小角度(本文称其为“莫尔角”),就会出现原子晶格在二维空间排布的莫尔条纹。该莫尔条纹周期性地调节层间耦合,导致系统的能带结构发生显著改变。这方面最著名的例子可能是Cao 等人做的转角石墨烯实验:当两层石墨烯之间的转角取所谓的魔角(1.08°)时,电子能带结构在费米能级附近出现平带,双层石墨烯呈现出莫特绝缘相。更神奇的是,在合适的外加偏压下,该异质结结构呈现出超导相[10-11]。莫尔晶格竟然在根本上改变了材料的性质!一石激起千层浪,该工作引发了vdW 异质结结构的理论和实验研究的热潮[12-17],甚至形成了一个专门的学科方向:扭曲电子学(twistronics)[18]。
vdW 异质结的研究也引发了物理学其他学科方向的相关研究。由于莫尔结构是通过将两个周期晶格堆叠所形成的,光学、声学、力学、热学以及冷原子系统等领域的研究者均可以通过构造类似的堆叠结构产生相应的莫尔晶格,如光学莫尔晶格[19-21],声学莫尔晶格[22-23],力学莫尔晶格[24]等。莫尔光晶格也被引入到冷原子系统,用来模拟凝聚态中的相关物理现象[25-26]等。这些莫尔晶格均显示出与转角密切相关的物理特性,在特定的角度下,结构中也会出现跟魔角石墨烯中类似的能带平坦化现象。
本文主要回顾和总结光学莫尔晶格方面的研究成果。
2 基于一维光栅的莫尔晶格
一维光栅是最简单的周期结构[29-34]。将两个晶格常数不同的一维光栅叠加,便可看到明暗相间的一维莫尔条纹(图1(a))。莫尔条纹的周期一般比两个构成光栅的周期要大得多,且莫尔条纹对光栅周期结构的微小变化十分敏感,因此莫尔条纹很早即被用于材料形变的分析和形貌测量[27-28],近期也被用于图案的防伪识别[29]等。
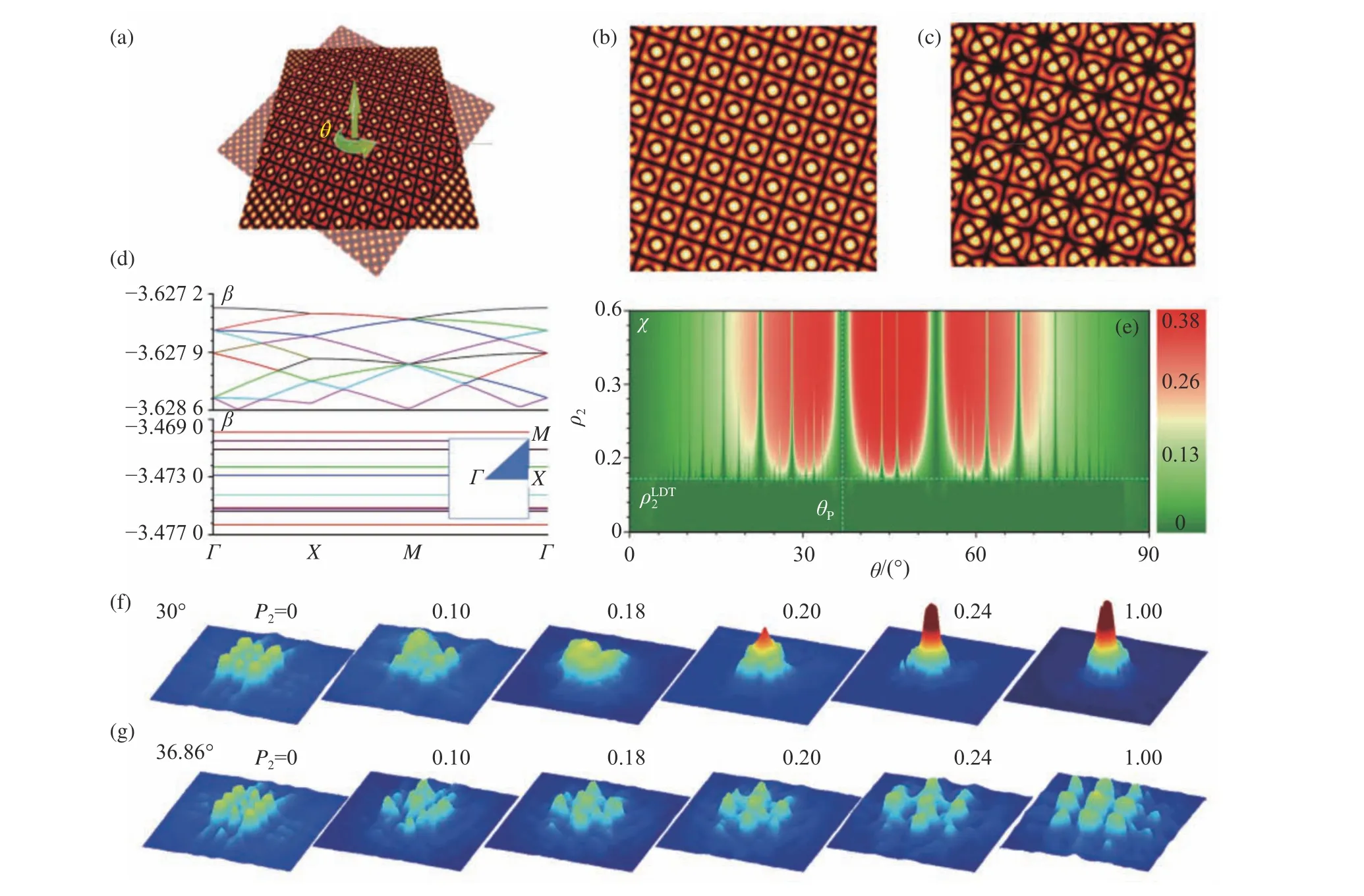
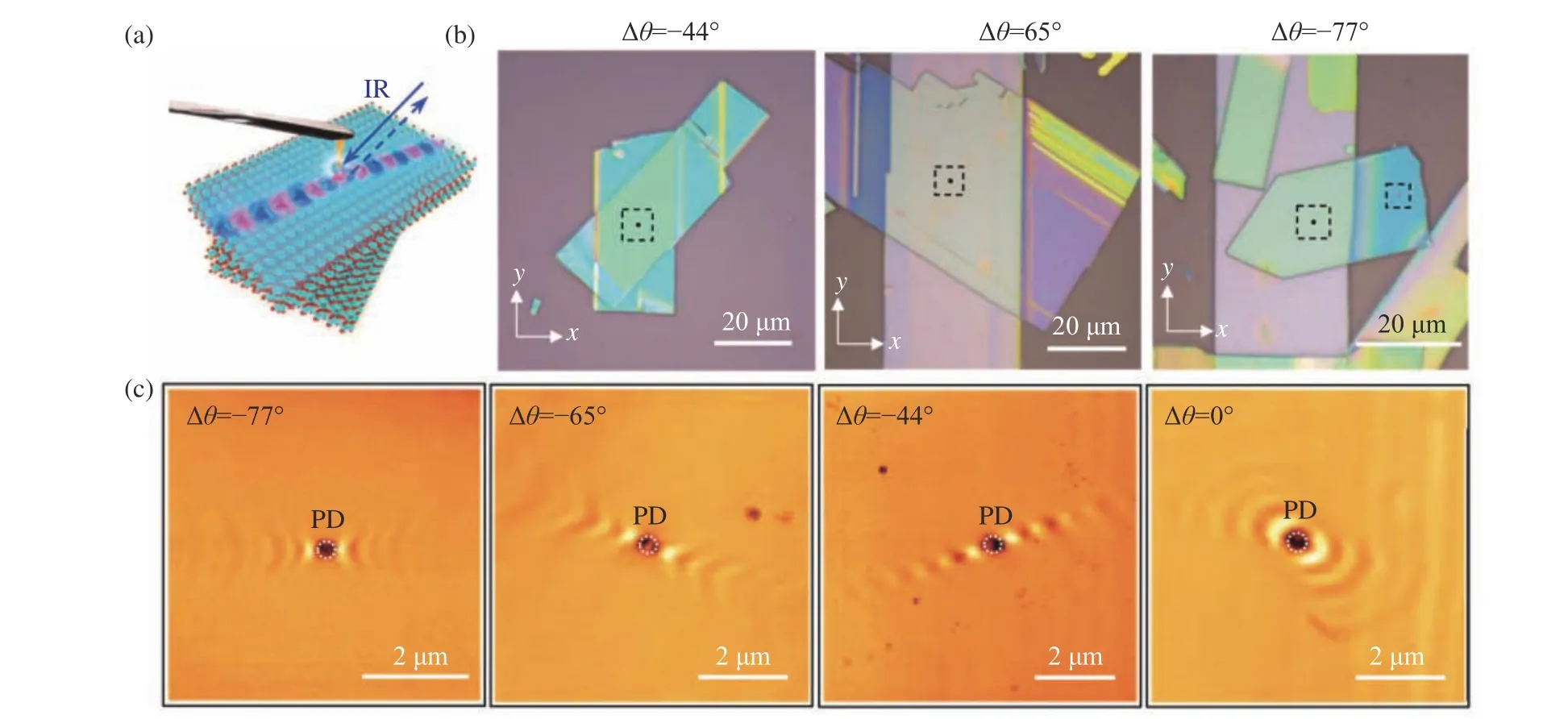
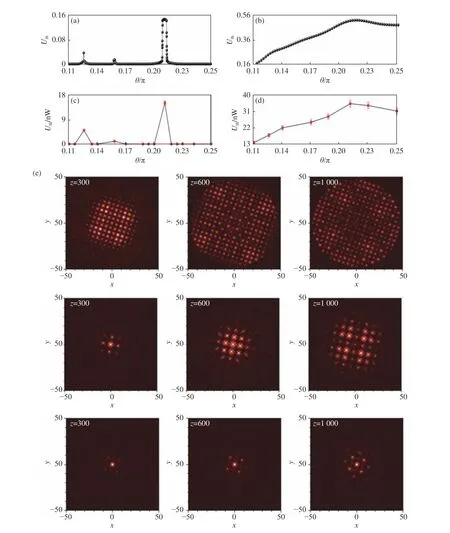
考虑两个周期分别为d1和d2的正弦函数,且它们的周期接近,即d2−d1< 上述慢光波导结构在机理上类似于光子晶体波导结构,即利用带隙导波。这种导波机制决定了电磁波在空间上可以限域在折射率较低处(图1(g))[33-34](图中光场在折射率低谷处的来回振荡是波导色散带的多个模式被同时激发而发生干涉所致)。有趣的是,数值研究表明,即使光一开始是在折射率高峰处入射,在后续的演化过程中也会逐渐耦合至折射率低谷处(图1(h)),说明一维莫尔晶格结构的节点处确实可以稳定地局域光与引导光。 图1 (a)由周期略有差异的两个一维光栅构成的莫尔光栅;(b)由两个周期相同的一维光栅,旋转一定角度后构成的二维莫尔光栅;(c)一个莫尔周期内的一维金属莫尔结构形貌图[32];(d,e)实验测得的金属光栅的SPP色散曲线和金属莫尔光栅的SPP色散曲线[30];(f)两个金属子光栅的周期(即d1,d2)发生改变时,相应的金属莫尔微腔辐射的激光发生频移[32];在一维莫尔晶格的节点(g)和最大包络处(h)激发莫尔晶格,光在晶格中的传输图像[34]。Fig.1 (a)Moirégratings constituted from two 1D gratings with slightly detuned periods.(b)2D moiré pattern constituted from two 1D gratings with a relative rotation angle.(c)Landscape of 1D metallic moiréstructure shown within one moiré period [32]. (d,e) Experimentally measured dispersion curves of SPP on metallic 1D gratings and on moiré gratings [30].(f)With the change of the period (i.e.d1,d2)of the two constituent metallic gratings,the lasing frequency of the corresponding metallic moirécavity changes[32].Light propagating dynamics when a 1D moirélattice is optically excited at its node (g)or at its peak (h)of the structural envelop[34]. 上述莫尔结构均由两个周期不同的一维光栅构成。通过互相转过一定的角度再重叠,两个一维光栅也可以构成一个二维周期结构—二维莫尔结构(图1(b))。显然,二维莫尔结构甚至可以由两个周期完全相同的光栅构成。该类莫尔晶格被用于增强钙钛矿太阳能电池的光电性能[35]。相比于单层的光栅结构,莫尔晶格的出现提高了单位角度内衍射级次和衍射光斑的数目,从而提升了光能的收集效率。研究表明,当转角为30°时,该太阳能电池对光的捕获和吸收效率达到最大:接近且部分超过传统的Yablonovitch 4n2吸收极限。由于该类莫尔结构的周期对转角的依赖高度敏感,故研究者可以通过转角自由度在很宽的频段范围内调控结构响应的共振波长。因此,莫尔结构被提议用于热辐射的动态管理,可大幅度提升热辐射管理器件频率的可调范围[36]。莫尔晶格为制备高效率的光电和光热器件提供了新的途径。 将两个二维周期结构重叠后,由于存在晶格常数差异或者彼此之间有相对转角,便能形成二维莫尔晶格。比起一维的情形,二维莫尔晶格在结构上更加丰富多彩,因此吸引了更多的研究。 首先是莫尔超表面方向上的工作。通过所谓的纳米球光刻技术(Moirénanosphere lithography),研究者在一些基底材料上制备了各类金属二维莫尔结构。相比于传统单周期的金属晶格,莫尔晶格包含了多个大小、方向不同的周期,因此可以在更多传播方向和更宽频率范围内激发表面等离子体激元(Surface Plasmonic Polaritons,SPP)[37]。当莫尔晶格中的金属在结构上没有联通的时候,则可以激发产生形态各异的各类局域等离子体共振(Localized Plasmonic Resonances,LPR)[38]。这些SPP或LPR 的工作频段可落在可见光或者近红外范围。通过纳米球光刻技术,研究者还将莫尔条纹刻写到单层石墨烯上,在莫尔图案化的石墨烯上激发了中红外和THZ频段的LPR,实现了共振频率的调控[39]。显然,如果将莫尔结构的特征尺度变大,比如在一些合适的基底材料上刻蚀出金属圆盘的莫尔排布结构,那么,当圆盘的半径和圆盘之间的间隔为毫米尺度时,将在GHz频段激发出各类准LPR,通过调节莫尔角可以将入射电磁波的透过率在10%−90%范围内连续调节[40]。 上述工作均是将莫尔结构引入到了薄层材料中,可称为莫尔超表面结构。莫尔结构也可以引入到体材料中,形成莫尔体结构:即沿着材料的某个方向(比如z向),在处于任意z处的横截面上均呈现为二维莫尔型的折射率分布。这种莫尔体结构可以通过光学诱导或者飞秒激光直写的方法在一些光敏材料中得以构建[19-20,41-42]。光学莫尔体结构的获得为研究光在莫尔晶格中的演化提供了条件。Huang 等人首先提出了莫尔晶格体结构的实现办法,并研究了光束在体结构中的传输动力学行为[19],即设想一体材料的折射率n(x,y,z)在z向(即光束的传输方向)分布均匀,但在其横截面(x和y轴组成的平面)内则为两个方形晶格的简单叠加:n(x,y,z)=p1[cos(2x)+cos(2y)]+p2[cos(2x’)+cos(2y’)],其中(x’,y’)T=S(θ) (x,y)T,S(θ)为二维旋转矩阵,即S(θ)=[cosθsinθ;sinθcosθ],θ即莫尔角。研究发现,对一般的莫尔角而言,当构成莫尔晶格的第二个子晶格的振幅p2小于某个临界值p2cr的时候(第一个子晶格的振幅p1固定为1,p1≡1),光束在相应的莫尔晶格中演化时持续地衍射发散;当p2超过该p2cr时,则光束始终保持局域的状态。这是首次在二维系统中发现的非局域-局域的相变。同时,研究也发现,当莫尔角取到所谓的勾股角(即θ是3个边长为正整数的直角三角形的内角)时,则对应的莫尔晶格恢复为方形周期晶格(但周期大于子晶格周期,并为复式元胞结构),因此,此时无论p2取何值,晶格中传输的光束始终处于发散状态。 以上理论预测得到了实验证实。Wang等人采用光学诱导[43]的办法,将8束平面波的干涉图样写入到光折变材料铌酸锶钡(SBN)晶体中[20]。这8 束平面波分成两组,前4 束平面波干涉在SBN中诱导出子晶格1,后4束平面波干涉则诱导出子晶格2。这两组平面波的强度和它们之间的转角在实验上容易调节,因此研究者得到了高度可调的光子莫尔晶格,见图2(a-c)。借此,Wang等人通过信号光(包括高斯光束和携带涡旋位相的光束)在各个莫尔晶格中进行传输测试,证实了关于光束局域和局域-非局域相变的理论预测,见图2(e-g)。进一步,他们通过构建其他各类型莫尔晶格(如基于三角晶格、斜方晶格、长方晶格[44-45]等各类基本晶格的莫尔晶格),证实了莫尔晶格中光束的局域和局域-非局域相变是一个普遍存在的现象。 图2 (a)由两个方形子晶格重叠,且转过相对角度θ 后,构成的二维光子莫尔晶格;(b)周期莫尔晶格;(c)非周期莫尔晶格;(d)非周期莫尔晶格对应的准能带图,上图p2 莫尔晶格为什么可以将光束局域?光的局域是信息传播的基础,也是对光信息进行各种操纵和处理的前提。光局域的常见办法有利用光纤(全反射机制)、光子晶体波导(光子晶体能隙)、随机结构(安德森局域)、非线性效应(如自聚焦机制)等。莫尔晶格中光的局域显然与上述体系中的局域机制均不同。为此,Wang 等人提出了“等效周期晶格”的概念,用一系列级次不断升高的周期晶格无限逼近(非周期)莫尔晶格,从而将非周期晶格的研究转化为成熟的周期系统的研究。借此办法,求解了光子莫尔晶格的准能带结构,发现:当p2>p2cr时,能带中存在丰富的平带(见图2(d),下图),平带意味着衍射振幅(正比于能带的曲率)为零,所以光束在莫尔晶格中自然地保持了局域的状态[20]。相比较地,当p2 平带是能带中一种特殊的存在,平带意味着波函数的局域化和态密度的剧增,这与许多强关联物理息息相关。因此,设计具有平带结构的人工微纳结构是一个具有重要价值的研究方向。平带设计的常见办法是采用具有特殊对称性的晶格[46-48]或者通过精心调节晶格参数得以实现[49]。一般而言,这些方法只能设计出一条特定的平带,而光子莫尔体晶格中则存在着丰富的平带结构。光子莫尔体晶格代表了一种得到平带的新方式。 上述二维光子莫尔晶格的体结构是通过光学诱导法产生的,这种方法能引入的折射率的变化很弱,仅为10−5~10−4量级,这和光子晶体结构中折射率的显著变化形成鲜明对比,后者一般由两种不同材料组成。文献[50]考虑了两个方形光子晶体构成的莫尔体结构,计算了莫尔角取某些特殊角时结构的能带。研究发现,由于复式元胞的出现,莫尔型光子晶体的能带带隙比单一方形光子晶体的带隙明显增大,这为光子晶体的能带设计提供了一个新的途径。然而,该工作仅仅考虑了取若干特殊莫尔角时的莫尔晶体的能带结构,关注点落在能隙的变化上,没有关于能带是否平坦化的讨论。 关于莫尔超晶格结构中能带平带的出现和影响,双层转角石墨烯材料的相关文献中有诸多讨论[51-53]。但需要特别指出的是,Huang 和Wang 等人研究的莫尔晶格是将两个周期晶格写入到同一块晶体中[19-20],属于单层(monolayer)莫尔晶格结构,而vdW 异质结则为双层结构。因此,这两者除了研究对象上有根本性区别之外(一为波色子,另一为费米子),在几何结构上也有明显的不同,因此这两类体系的研究结论不能直接拿来对比。然而,非蜂窝状周期晶格构成的莫尔结构也存在能带平带的发现,对二维材料的相关研究具有明显的启发和借鉴价值。 受二维材料堆叠形成的vdW 异质结结构研究的影响,近期关于光学双层莫尔结构的研究也陆续出现[54-56]。Hu 等人研究了双层α 相三氧化钼(α-MoO3)超结构中声极化激元(声子与光子耦合形成的准粒子)的传播行为[55]。α 相三氧化钼是一种双曲(Hyperbolic)材料,即在其面内两个相互垂直的方向传输时,准粒子感受到符号相反的介电常数,此时色散关系为双曲线类型。然而,研究人员发现,在α 相三氧化钼的两层堆叠结构中,当转角超过一定值时,由于准粒子间的层间耦合,色散关系从原先开放的双曲线过渡为闭合的椭圆曲线(图3),即在某个特定的转角处(研究者称其为光子“魔角”),色散关系呈现为一平带,这意味着声极化激元无衍射地定向传输。因此,通过控制莫尔角,研究人员在同一结构上实现了三种不同类型的色散关系曲线(双曲-平带-椭圆)相继转换,展示了莫尔结构对极化激元大范围的动态调控。 图3 (a)两层α-MoO3堆叠构成的莫尔超晶格结构;(b)α-MoO3莫尔超晶格结构在不同莫尔角下的光学照片;(c)声极化激元在不同莫尔角度下的波形分布图,显示出双曲-平带-椭圆三类拓扑上不同的色散带的转变[55]。Fig.3 (a)Moirésuperlattice constituted by twist-stackedα-MoO3 bilayer;(b)Optical images of α-MoO3 moirésuperlattice as a function of rotation angle;(c)In-plane propagation of phonon polaritons at different twist angle of an α-MoO3 bilayer,indicating a transition among three topologically different dispersion:hyperbolic,flat and elliptic[55]. Wang 等人则考虑双层莫尔超结构中的另外一种极化激元,即准表面等离子体激元(Spoof SPP,该类激元可看成是传统SPP在微波等长波波段的存在形式)[57]。他们考虑在厚度一定的薄介质层上表面和下表面分别附着呈蜂窝状晶格排布的金属环结构,该类超表面结构支持Spoof SPP。上下表面的耦合使得Spoof SPP产生模式杂化,情况类似于堆叠二维材料通过分子力产生的层间耦合。研究者发现,当上下蜂窝状晶格在某个维度方向上的晶格常数有所差异时(该工作中未考虑转角非零的情形),复合结构中出现的周期性变化的莫尔条纹使得Dirac点在布里渊区移动,从而引入了电中性粒子(光子)的规范势和等效磁场,后者被在实验上观察到的平坦化朗道能级所证实。进一步地,如将转角自由度引入到该类莫尔结构中,则vdW 异质结结构具有的一些与能带相关的重要性质也可以在光子莫尔晶格中重现,如在合适的转角和层间距下,光子能带出现平坦化、莫尔晶格边缘处存在拓扑局域模等[58]。 上述双层光子莫尔晶格的工作关注极化激元在面内的传输动力学行为,这种双层结构对面外如垂直入射光的散射如何响应?Liu 等人将两个超透镜(二维位相型光栅)置于传统的光学成像系统中,通过调节两个超透镜的相对转角,实现了对成像焦平面位置和聚焦光斑形态的调控[59]。Lou 等人则分析了两层光子晶体层状结构(PhCslab)互相转过一定角度之后形成的异质结结构的光散射特性[56]。他们在理论上提出了一个对应原理:对于双层光子晶体层状结构堆叠而成的莫尔晶格,其支持的导波共振(Guided Resonances)频率,可以用单层光子晶体和一均匀层状材料的堆叠结构很好地近似。由于后者为一周期结构,因此传统的能带理论可以直接用来求解、预测双层堆叠结构的光学响应,从而大大降低数值计算的复杂度。研究者进一步揭示了该类光子莫尔结构的光学手性响应特征[56]。 光子莫尔晶格极大地改变了结构的色散关系,如能带平坦化或者能带发生拓扑上的改变。能带的改变如何影响传统的非线性光学过程,如光孤子的形成、非线性波长转换过程等? 非线性光子莫尔晶格的研究最早见于莫尔晶格中空间光孤子的研究[19,21]。空间光孤子是光的衍射效应和非线性效应互相平衡、从而在传输过程中保持空间波形不变的光束[60]。空间光孤子被认为在信息传输、全光路由、光控光等方面具有独特的应用价值。然而,材料的非线性响应一般非常微弱(相比于线性响应),因此在体材料中激发光孤子一般需要很高的激光功率。人们也研究了各种周期结构中的空间光孤子,周期结构提供的能带设计可以较好地降低光束的衍射效应,从而降低光孤子的激发对激光功率的要求。研究者还考虑了包括金属纳米线阵列结构在内的各类等离子体晶体(Plasmonic Crystals)中空间光孤子的激发[61],借助于SPP的场增强效应也可降低孤子的激发功率。然而,由于金属纳米线自身的热稳定性问题,目前尚未见到等离子体格子孤子的实验观察。 Fu 等人通过光学诱导的办法,在光折变晶体(铌酸锶钡)中产生光子莫尔晶格。在施加偏压的条件下,铌酸锶钡具有饱和型非线性响应,这就相当于在光子莫尔晶格中引入了光学非线性响应。理论和实验研究发现,光子莫尔晶格中光孤子的阈值激发功率明显依赖于莫尔角。图4(b)和图4(d)给出了当线性莫尔晶格处于非局域相(即p1≡1,p2 图4 (a-d)激发莫尔光孤子的阈值功率随莫尔角的变化,(a,c)对应p2>p2cr 的情形,(b,d)对应p2 最后,也有研究者报道了二次非线性介质中莫尔光孤子的数值研究[62],发现莫尔孤子在参数空间中的存在区域与莫尔角无关,但孤子的稳定性则依赖于莫尔角。另外,具有自聚焦效应的一维莫尔晶格中也有光孤子数值研究的报道[63]。 Cao等人的工作引发了转角石墨烯研究的热潮[9-10],这方面工作主要集中于转角石墨烯的电子特性,但也有不少研究人员开始研究它们的光学特性。石墨烯支持THz 或者近红外波段的SPP,其波长可比光子波长小3个数量级[64-65],且由于损耗相对较低和电学特性的可调性,石墨烯被认为是一种性能优良的等离子体材料。Sunku 等人提出了利用双层石墨烯莫尔晶格产生周期性等离子体结构,从而在原子尺度上实现对SPP的各种调控[66]。人们也发现了双层石墨烯中的SPP激发具有手性和圆二色性[67-69],且SPP在不同的莫尔结构构成的畴壁处有不同的反射行为[66,70]等。 除了石墨烯,莫尔结构也会影响其他二维材料的光学性质,比如过渡金属硫族化合物(TMDCs)。通过叠加、旋转两单层TMDCs,同样可以产生原子在空间分布上的莫尔条纹,从而改变这些材料中准粒子的特性,为新型光电方面的应用提供新的可能[71-72]。类似地,通过莫尔角和层间耦合的控制,人们也实现了对二维材料异质结结构的非线性光学响应的调控[73-78]。 莫尔晶格通过将两个周期晶格简单叠加得到,但呈现出两个组成晶格所不具有的物理特性,是“一加一大于二”的又一个明证。光子莫尔晶格提供的能带平带化开辟了一条获得光子平带和光束局域的新途径,也为各类光场的空间调控提供了一个新平台。根据其具体实现方式,光子莫尔晶格所具有的一些独特的设计自由度,如莫尔角、子晶格之间的耦合力度、两个子晶格的相对比重,为光场的动态调节提供了新的设计自由度。莫尔晶格是处于周期和随机结构之间的一个中间相,相当于较为成熟的周期和随机系统的研究,光学莫尔晶格的研究刚刚起步。已经取得的研究结果表明,准周期或者非周期结构可能具有周期系统完全不具有的光学性质,可为光的控制提供独特的手段。我们相信光学莫尔晶格将会吸引更多的研究,得到更多的莫尔晶格的光学实现,并在揭示其奇特光学特性的基础上得到一些特殊的应用。
3 基于二维周期结构的莫尔晶格
4 莫尔晶格中的非线性光学现象
5 双层石墨烯莫尔晶格
6 结束语