二维人工超材料的光学拓扑性质

苏照贤，姚恩旭，黄玲玲，王涌天

（北京理工大学光电学院北京市混合现实与新型显示工程技术研究中心，北京 100081）

1 引 言

人工超材料（Artificial Metamaterials）通过人工设计亚波长单元结构，控制亚波长单元与电磁波的相互作用，提供了一种任意操控电磁波的新方法[1]。但是三维块体超材料的实际应用有两个难以避免的挑战：在光学波段巨大的损耗和极大的加工制备难度。以超表面（Metasurfaces）为代表的二维人工超材料为解决以上两个问题提供了方案。超表面是三维超材料的二维等价物，相比于三维超材料，二维超表面具有更薄的厚度、更低的损耗，同时，可以实现三维超材料几乎全部功能，如光束偏折、偏振转换、聚焦、全息成像等[2-7]。当前，具有非平凡拓扑性质的光学结构，由于其受拓扑保护的边界态具有免疫局部缺陷，无向后散射的单向传播的奇特光学性质，成为了光学领域的研究重点，受到广大科研工作者的关注[8-9]。

拓扑是一个数学术语，涉及研究几何对象在连续变形下的守恒性质。从1980年开始，随着物理学家发现了整数量子霍尔效应和量子自旋霍尔效应，物质的拓扑相得到了广泛的研究，拓扑绝缘体领域开始蓬勃发展[10-16]。拓扑绝缘体可以在其表面传导电子，而在其内部则充当绝缘体。在带隙内，即使存在杂质，它们的表面电子也可以无耗散地传输。受凝聚态物理领域中这些激动人心的突破启发，2005年，Haldane和Raghu 把拓扑概念拓展到光子学中，提出了光子系统中的拓扑相，拓扑光子学从此成为了一个蓬勃发展的新兴领域[17]。拓扑光子晶体可以被看做光学中的拓扑绝缘体，它具有受拓扑保护的单向传播边界态。光子学中材料的拓扑性质是通过光子能带在整个布里渊区的波函数来定义的，它一般由一个整数表示，这个整数也就是光子材料的拓扑不变量[18-19]。当两种具有不同拓扑不变量、带隙处于同一频率范围的光学材料相互接触时，将会在材料界面发生拓扑相变，出现连接导带和价带且局域于两种材料边界上的边界态。由于拓扑保护，这个边界态不会受到微小扰动的影响，也就是说该边界态光的传输并不受局部缺陷的影响；同时由于该边界态独特的色散性质，该边界态上的光具有鲁棒的单向传输性质，也就是说光能够沿边界单向传输并且没有背向散射。基于拓扑光子学的光波导可以实现低功率、高保真的稳定光学通信，具备很强的抗干扰能力，为研发设计光子芯片、新一代光计算元件提供了理想平台。

光学拓扑材料的光学性质受到对称性的保护，当材料中的扰动不足以打破这种对称性时，其性质会稳定存在。在设计光学中的二维量子霍尔效应系统和三维外尔半金属这些具有非平凡拓扑性质的材料时，需要打破时间或者空间反演对称性，人工超材料在设计这类光学拓扑材料方面有着天然的优势，其可以通过结构设计打破材料某一方面对称性以此获得非平凡的拓扑性质：如通过超材料结构中耦合磁光材料打破时间反演对称性，利用非对称结构分布打破空间反演对称性。具有非平凡拓扑性质的二维人工超材料由于有着易于片上集成、损耗低等优势，在光学领域中得到了极大的关注。本文介绍了二维光学拓扑材料的几种类型和研究进展。首先，本文介绍了通过打破时间反演对称性实现的二维光学拓扑结构。随后，本文介绍了保持时间反演对称性，具有Z2拓扑不变量的非平凡光学拓扑材料。接着本文介绍了通过构建人工合成维度的方法，在一维和二维人工超材料上实现外尔点。最后，本文对二维光学拓扑材料的发展进行了总结与展望。

2 打破时间反演对称性的二维光学拓扑材料

根据Haldane在1988提出的Haldane模型，在石墨烯体系的哈密顿矩阵中加入次近邻耦合项，可以打破时间反演对称性，从而获得非平凡的拓扑性质[17,20]。二维系统的拓扑不变量，也可以被称为陈数（chern number），可以通过下式计算[10]：

2005年，Haldane和Raghu 在之前研究的基础上，利用磁光材料构建光学超材料打破时间反演对称性，可以获得光学中的整数量子霍尔效应：该光学周期超材料带隙下的能带具有非零的拓扑数。当带隙处在同一频率，且具有两种不同拓扑数的超材料接触在一起时，在其边界会发生拓扑相变，产生无带隙的单向传输边界态[17]。随后，Wang 等人设计了一种工作频率在微波频段的旋磁材料周期阵列结构，具有非零的陈数以及单向传输边界态，并且进行了实验验证[21-22]。图1（a）中是他们所制备的光学拓扑超材料示意图，图1（b）从上到下分别是实验测得的体透射系数，计算得到的能带图和实验测得的边界透射系数，实验结果证实了他们所制备的光学拓扑超材料实现了免疫局部缺陷的无后向散射的边界态电磁波传输。Wang等人实现的拓扑光子晶体的陈数为1，对应着一种单向传播的波导模式，Skirlo等人研究了在光学结构具有更大陈数时，可以拥有多个单向传播的波导模式[23]。Skirlo等人研究了两种方法增大二维光学结构的陈数：第一种方法是增加系统的对称性，使在同一频率处的简并点的数量倍增；第二种方法是将多个对称性无关的简并点调整在同一频率范围内发生，在施加磁场打破实验反演对称性并产生带隙后，可以使光学系统具有更大的陈数，并理论证明了最大陈数为4的拓扑光子晶体。随后，Skirlo等人利用铁磁材料光子晶体实验验证了理论预测，如图1（c）所示。实验结果显示，当外加磁场变化时，样品具有的陈数可以为2、3和4，如图1（d）所示。这与理论分析相符[24]。

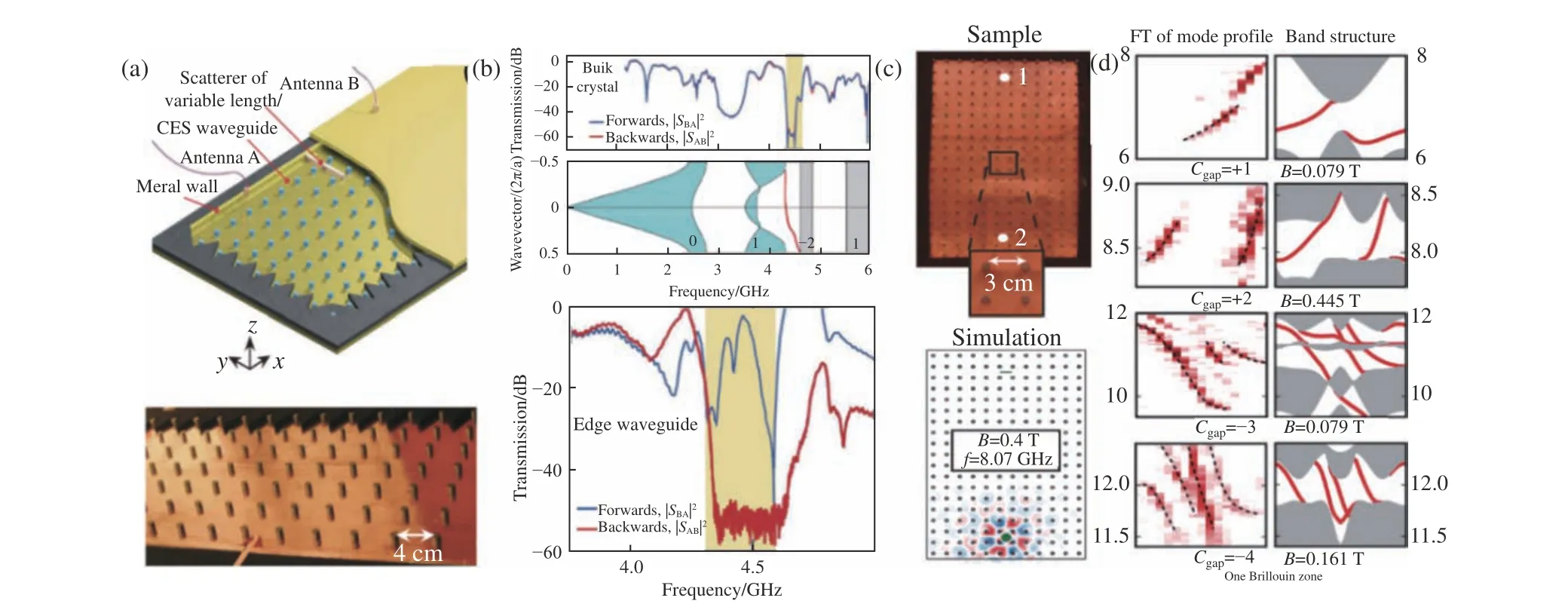
图1 (a)利用旋磁材料制备的光学拓扑超材料示意图；（b）实验测试得到的体透射系数，光学拓扑超材料的能带图（标签为能带的陈数）[21]，实验测得的边界透射系数；（c）大陈数拓扑光子晶体的实验样品以及仿真结构；（d）实验和计算得到的能带结构[24]Fig.1 (a)Structure diagram of optical topological metastructure fabricated by gyromagnetic material;(b)experimental bulk transmission and band structure of optical topological metastructure[21];(c) topological photonics crystal sample and simulation scheme with large chern number;(d) band structure obtained by experiment and calculation[24]

3 具有Z2 拓扑不变量的二维光学结构

以上几个光学拓扑结构都是利用磁性材料打破时间反演对称性获得非平凡的拓扑性质，然而在光学结构中实现起来并不方便，而且磁性材料很难被用在光学频段，因此需要研究者们设计出无需打破时间反演对称性的光学拓扑超材料。2005年，Kane和Mele提出量子自旋霍尔效应，对于能带上不同自旋的电子具有相反的陈数[11-12]。在系统具有时间反演对称性的情况下，能带总的陈数为0，但对不同自旋电子的陈数差不为0，系统边界具有对不同自旋电子的手性边界态。这时具有时间反演对称性的系统的拓扑不变量可以用Z2拓扑数分类，Z2=0时系统是普通绝缘体,Z2=1时系统是拓扑绝缘体[25-27]。系统的拓扑数为[28-29]：

光子的自旋和电子的自旋有很大不同，在光学系统中实现需要人工超材料构建赝自旋来实现。Hafezi 等人利用相互耦合的环形波导谐振腔阵列证明了光学中的自旋量子霍尔效应[28-29]。通过采用的环形谐振腔支持顺时针模式和逆时针模式，可以被认为自旋向下（σ=−1）和自旋向上（σ=1），构建一对赝自旋。环形谐振腔之间通过倏逝波耦合，通过排列各个环形谐振腔之间的位置，可以构建一个具有人工磁场的哈密顿矩阵，如图2（a）所示，在每个单元上光的传播具有2πασ相位累积，从而不同赝自旋的光具有相反的规范场，并且他们还利用红外相机实验拍摄到了边界态传播，如图2（b）所示。2018年，Harari和Bandres等人理论证明了环形波导阵列构成的拓扑激光谐振腔能够在边界具有单向的单模激光激发，即使有缺陷，激光效率也不会降低[30]。为了证明以上理论研究的正确性，利用在包含InGaAsP量子阱的基底上制备了10×10个耦合环形谐振腔，如图2（c）所示，在波长为1064 nm 的纳秒激光泵浦下可以获得鲁棒的高效单模激光[31]。同时，对拓扑激光器和不具有非平凡拓扑性质的耦合环阵列激光器在不同泵浦强度下的激发光谱进行对比，如图2（d）所示，证明了拓扑激光器具有更好的单模性。

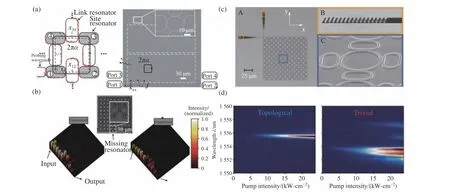
图2 （a）单个单元的耦合环形波导示意图以及实验测试系统；（b）实验测试得到免疫缺陷的鲁棒的边界传输[28]；（c）拓扑激光器结构SEM图；（d）拓扑激光器和拓扑平凡激光器在不同泵浦强度下的激发光谱[31]Fig.2 (a)Scheme diagram and experimental setup for each ring coupling unit;(b)defect-imunne robust edge transmission by experimental mearsurement[28];(c)SEM imagesof topological laser;(d)emission spectra of topological and trivial laser under different bump intensity[31]

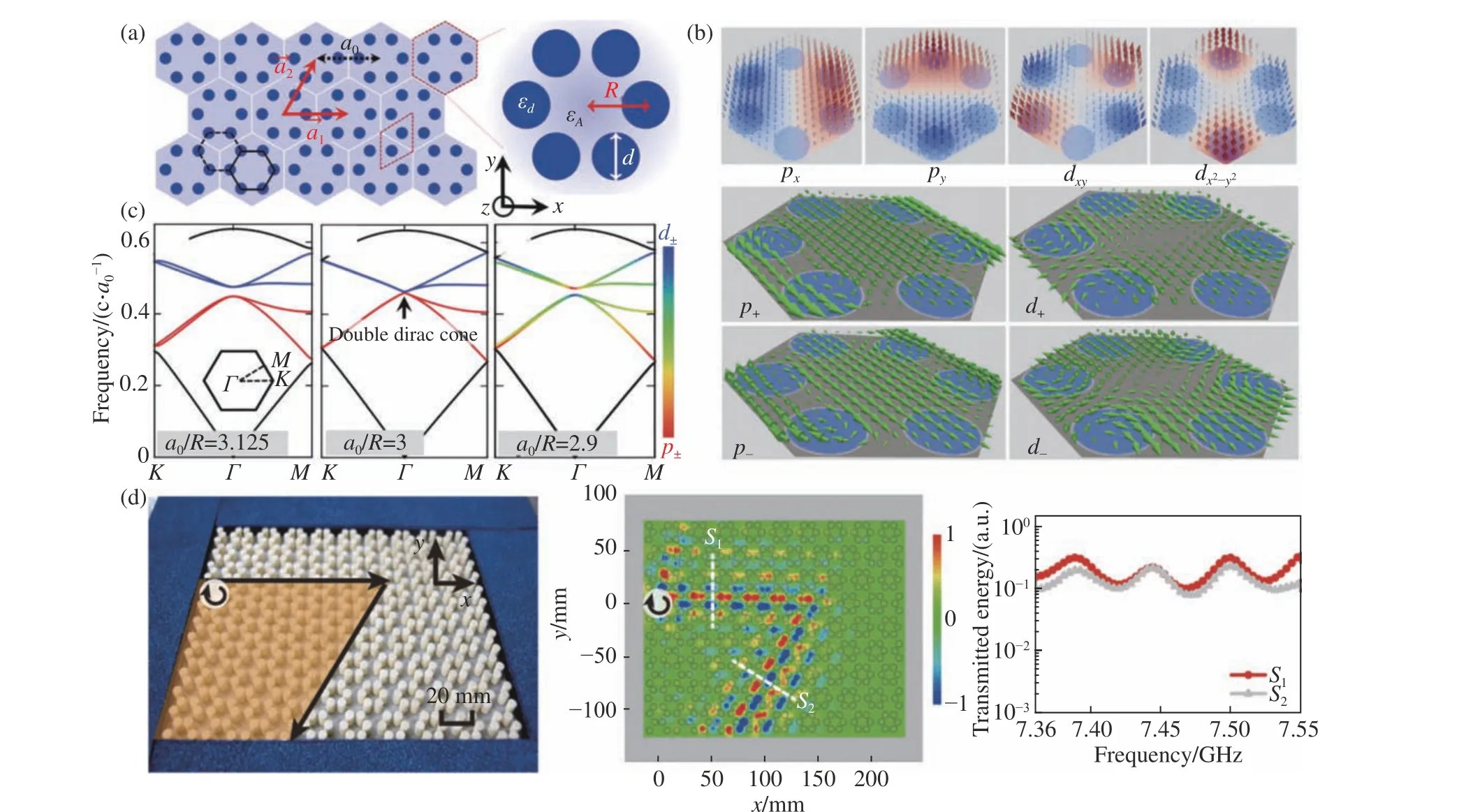
图3 （a）拓扑光子晶体示意图[32]；（b） px(py)和d xy(dx2−y2)构成的赝自旋态[32]；（c）光学拓扑结构能带图[32]；（d）Al2O3柱构成的光学拓扑结构、实验测试得到的7.41GHz频率时场分布、在S1点和S2 点的透射强度[34]Fig.3 (a)Schemeticdiagramof topologicalphotoniccrystal[32];(b)pseudo-spin statesof px(py)anddxy(dx2−y2)[32];(c) band structure of topological optical structure[32];(d)topological optical structure consisiting of Al2O3 pillars,field distribution with frequency of 7.41 GHz in experimental,transmitted energy at S1 and S2[34]

受到二维材料谷电子学和谷霍尔效应的启发，能谷成为了调控材料性能的一个新的自由度[40-42]。2016年，中山大学的董建文教授提出利用能谷自由度实现自旋分离[43]。图4（a）是他们设计的一种蜂窝状晶格的光学超材料，每个单元里包含两个双各向异性，且介电常数和磁导率相等的柱子，由于电磁对偶对称性，麦克斯韦方程在这种情况下可以分为两种赝自旋子空间，当Ez和Hz同相位时，代表自旋向上，相位差为 π时，代表自旋向下。通过在单元中的两个柱子引入不同的电磁耦合系数 κ1和 κ2来打破空间反演对称性，可以打开带隙产生自旋分离，如图4（b）所示，在带隙中，可以使自旋向下和自旋向上的模式分别沿ΓK和ΓK′方向传播，而在带隙外，上下自旋的电磁波会混合在一起。这种光学超材料的拓扑性质由电磁耦合系数 κ1和κ2的差值贡献，在不同拓扑相结构的边界具有受拓扑保护的平边界态，如图4（c）所示。

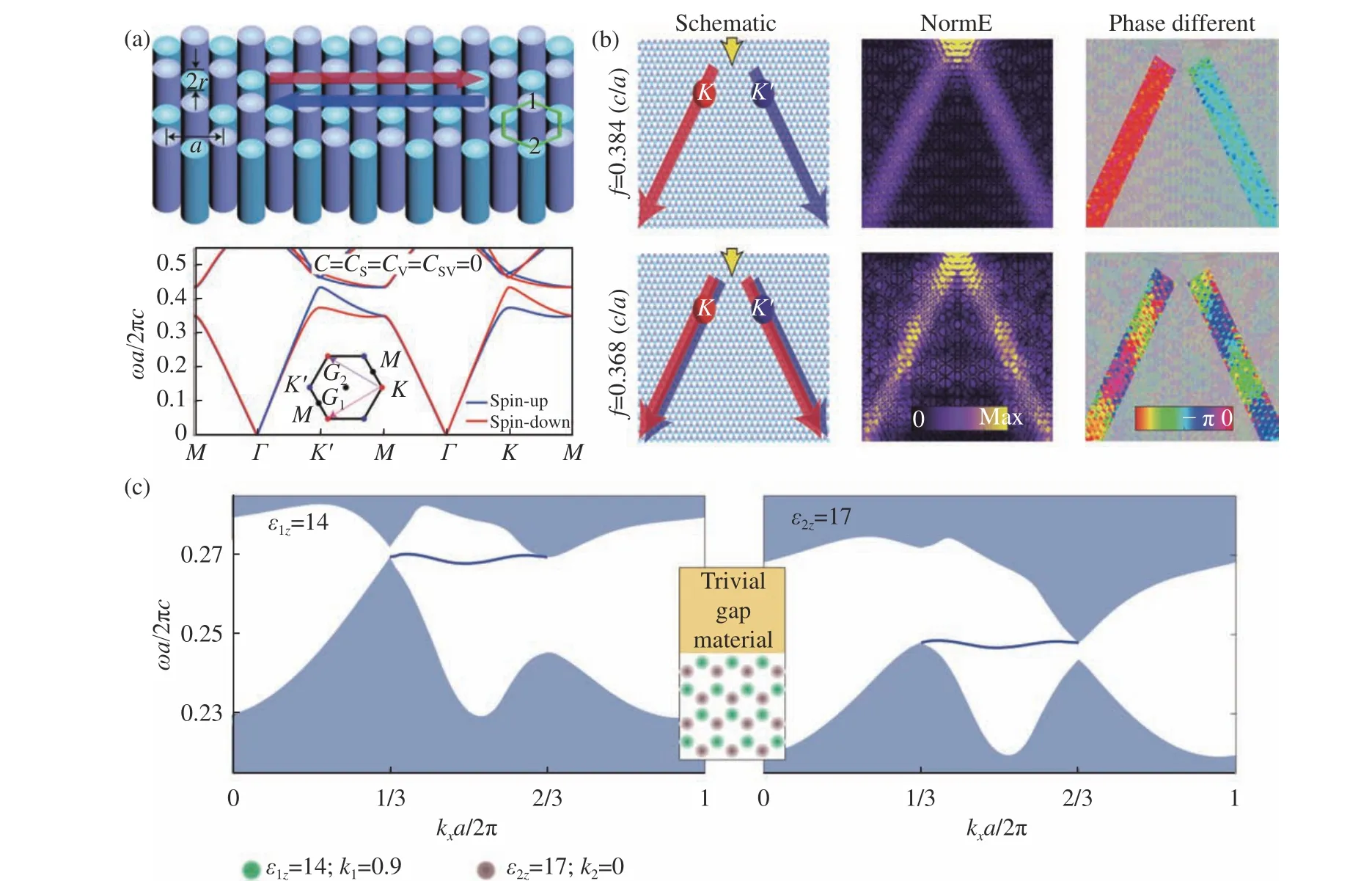
图4 （a）利用能谷自由度设计的光学拓扑结构[43]；（b）能谷依赖的光学拓扑结构的自旋分离行为[43]；（c）左右分别为介电常数为14 和17时自旋向上的体态投影以及受拓扑保护的平边界态[43]Fig.4 (a)Optical topological structure designed by energy valley freedom[43];(b)spin separation behavior in valley dependent optical topological structure[43];(c)flat edge dispersions in a photonic crystal with different permittivtities.Only the spin-up polarized projection bands(shaded blue region)and the spin-up edge statesareillustrated [43]

接着，Xin-Tao He等人利用谷自由度设计并制备了一种绝缘体上的硅光子晶体超材料[44]。他们所设计的硅基拓扑光子超材料可以工作在通信波段，在直线形、Z形和Ω形3种形状的光学路径下都测量出在周期单元频谱能带带隙内的高透射，图5（a）和图5（b）证明了该结构的拓扑保护性质。同时，他们利用硅微盘的顺时针和逆时针模式可以选择性地激发拓扑边界态，实现了亚微米量级耦合长度的宽带光子路由行为，如图5（c）和5（d）所示。最近，新加坡南洋理工的研究者Yihao Yang 等人设计制备了一种带有不同大小三角形孔的全硅芯片，实现了太赫兹频段的能谷依赖的拓扑数据传输[45]。他们所设计的太赫兹芯片可以沿高度弯曲的路径传输数据，最快可以达到11 Gbit/s的数据速率，能够支持4K 高清视频的实时流传输，为6G 通信提供技术基础。能谷依赖的光学拓扑结构由于其设计的方便性，已经被广泛应用到光学拓扑超材料的设计中[46-53]。

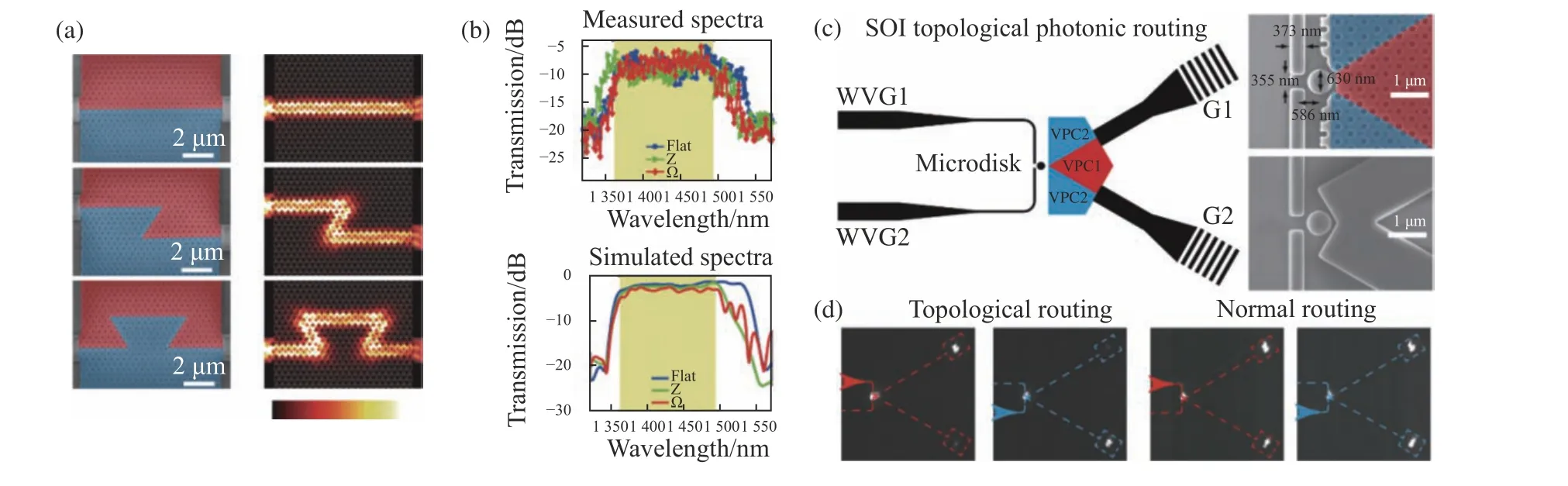
图5 （a）利用硅基板设计的具有不同边界的能谷依赖光学拓扑结构[44]；（b）实验和仿真得到的对不同边界路径的透射[44]；（c）光子路由示意图[44]；（d）光子路由的拓扑光传输[44]Fig.5 (a)Topological optical structure on the substrate of Si with different boundary[44];(b)transmission spectra obtained by experiment and simulation[44];(c)schemetic diagram of photon route[44];(d)topological optical transimission of photon route[44]

4 具有合成维度的拓扑结构

除了在二维动量空间中由波函数定义的拓扑绝缘体，在三维系统中也存在贝里曲率的奇点外尔（Weyl）点，具有外尔点的物质也被称为外尔半导体。外尔点是三维动量空间中两条能带的线性简并点，是贝里曲率的源点或者汇聚点，往往被看作是动量空间中的磁单极子，外尔半导体因为有着受拓扑保护的边界态、手性异常等奇特的性质而备受关注，目前已有很多具有光学中外尔点的超材料被设计并制备出来[54-59]。

由于三维块体材料本身存在体积巨大不易于集成、损耗大等不利因素，因此在二维光学结构上构建合成维度来实现光学外尔点对片上集成光学的发展具有重要意义。所谓合成维度，可以理解为动量空间中引入的人工维度，即通过选择系统中已存在的参数或者引入人工可调控的参数构成参数空间，以突破几何维度的限制。合成维度由于其本身具有可调控性，使得外尔点与外尔节线之间的相互转化成为可能，为系统地研究结构拓扑性质提供了便利。所谓“外尔节线”，是半金属材料中能带的交叉点在晶格动量空间形成连续的闭合曲线，也就是能带的二重简并线。在合成维度研究外尔点的性质有两个优势：（1）合成维度拓扑结构能够研究高维度外尔点性质；（2）合成维度灵活的控制手段使得在实验上研究任意包围外尔点的闭合曲面上的拓扑现象成为可能[60]。

近年来，各种各样的合成维度拓扑绝缘体的实现方法已经成为了研究热点。探索新型加工工艺，以提升器件制备精度，使得深层次探索合成维度拓扑性质成为可能[61]。基于动态调制谐振环系统的高维度拓扑研究取得了很大进展，在高阶参数空间中不同维度上具有新奇的拓扑性质[62-65]。

2017年，南京大学的Qiang Wang 等人设计了一种一维光子晶体结构[66]。如图6(a)所示，基于布拉格定律，在保证等效光程不变的前提下，通过引入与介质层厚度相关的两个人工参数p和q，构造一个三维人工参数空间。该工作在实验上首次证明了一维光子晶体中合成外尔点的存在，其能带图如图6(b)所示[66]。另外，可以在时间维度上对每一介质层的等效折射率和厚度进行人工控制，实现对拓扑界面态的精确调控。如图6(c)和6(d)所示，合成外尔点附近的反射相位呈现涡旋分布，且光子晶体截断面处的反射相位呈现“费米弧”类似分布，从而保证了光子晶体与任意反射衬底之间界面态的存在。最后，文献[66]还指出，通过改变参数空间的选取方式，在保证系统总拓扑荷数不变的条件下，实现了合成外尔点与“外尔节线”之间的相互转化。该工作通过改变人工参数大小，实现对界面状态的控制，产生的反射相位涡旋为产生涡旋光束和控制反射方向生成提供了一种新的方法。当利用更多参数时，有望获得简并外尔点和高阶外尔点，为研究片上光子态免疫缺陷传输的条件提供了新思路。

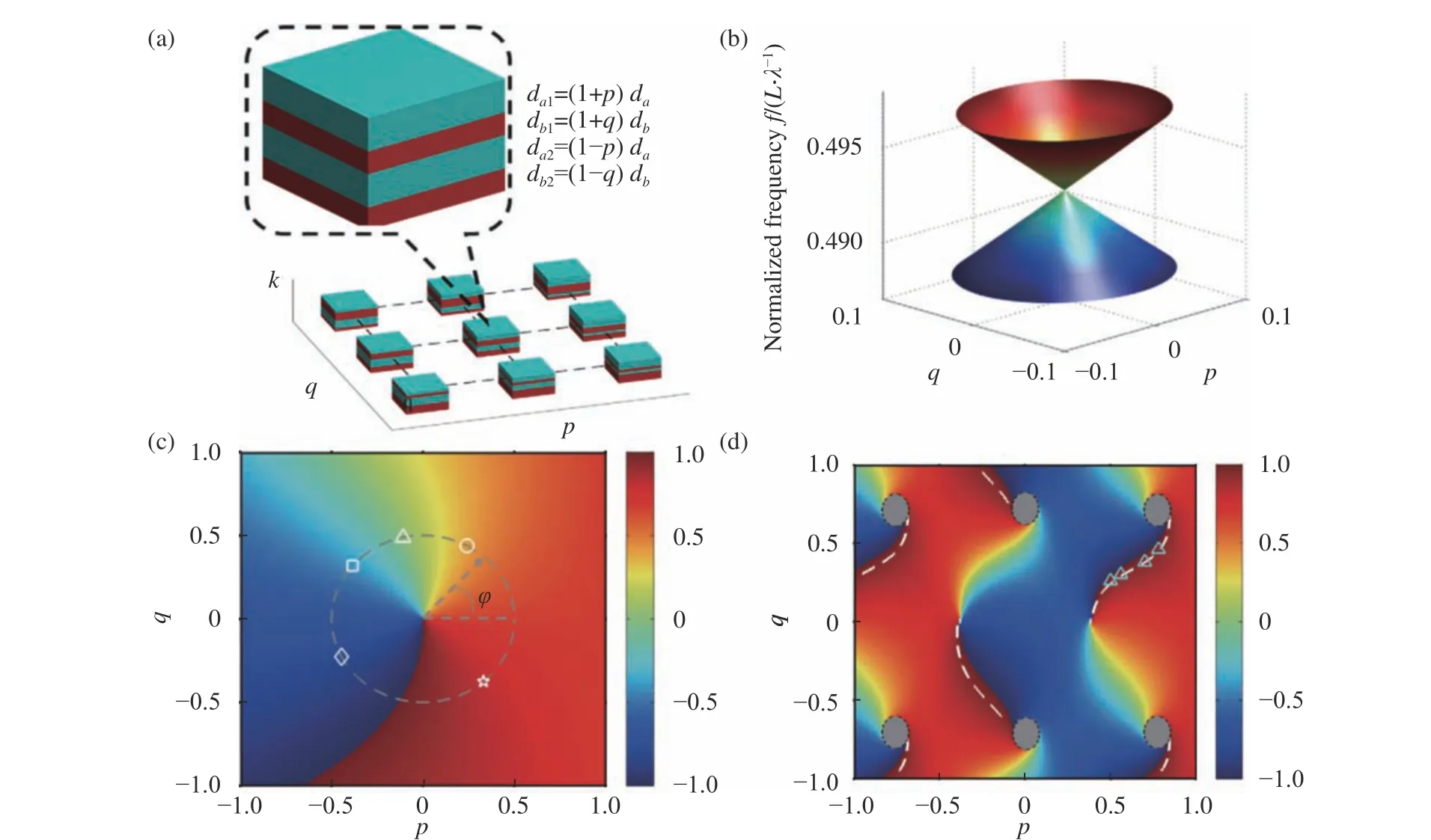
图6 （a）利用介质层厚度构建参数空间示意图[66]；（b）在三维合成维度中的人工外尔点[66]；（c）光子晶体截断面上的反射相位分布[66]；（d）在外尔点频率处的反射相位，白色虚线为费米弧轨迹[66]Fig.6 (a)Schematic diagram of parameter space constructed by dielectric thickness[66];(b)artificial Weyl point in 3 synthetic dimensional topological structure[66];(c) reflection phase on the truncated face of photonic crystal[66];(d) reflection phase at Weyl point,Fermiarc is marked in white dashed line[66]

2016年，斯坦福大学的Qian Lin 等人设计了一种二维蜂窝状谐振环阵列结构，如图7(a)所示，通过对每个谐振环的不同位置引入外置的电-光调制作为合成第三维度方案，实现了不同谐振环之间的静态耦合和人工可控调制[67]。将该模型看做波导振幅模型来处理[68]，可构造出具有不同拓扑电荷数的人工外尔点，进而在同一结构中产生多重拓扑表面态。通过引入合成维度作为第三个维度，该工作成功地在二维谐振环阵列结构中实现了可控人工外尔点。相比之下，二维谐振环阵列具有更简单的几何结构和更高的调制自由度，为利用片上光学平台挖掘人工外尔点的物理特性提供了方法。不仅如此，该模型能产生多重拓扑态，在对称性破缺条件下，通过动态调制相位，实现了从“外尔节线”到人工外尔点的转化。在丰富新型拓扑效应的同时，为其他蜂窝状晶格结构中拓扑功能的实现提供了思路。

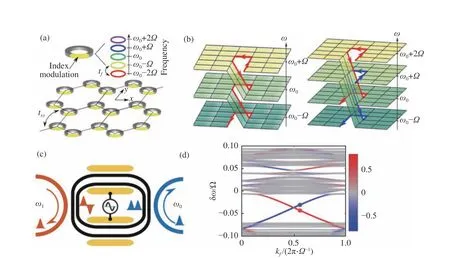
图7 (a)二维蜂窝状谐振环阵列结构示意图[67];(b)频率空间上的螺位错示意图；(c)动态耦合谐振环示意图；(d)拓扑保护态能带图[69]Fig.7 (a)Schematic diagram of 2D honey-comb resonator arrays[67];(b)schematic of helical dislocation in frequency space;(c)schematic diagram of dynamic resonator;(d)band structureof topology-protected states[69]

2018年，Qian Lin 等人设计了另一种二维谐振环结构实现三维光子拓扑绝缘体。他们所设计的二维谐振环支持一系列离散模式，形成频率梳[69-71]。通过在二维谐振环上添加第三维人工调制维度，可使二维谐振环变成三维拓扑绝缘体。如图7(b)所示，在该合成维度体系中，通过调制一部分谐振环的共振频率，会在人工频率轴上形成“螺位错”，这种“螺位错”现象支持沿人工频率轴单向传输的拓扑保护模式。实现人工频率的动态耦合的关键是设计动态耦合谐振环。如图7(c)所示，蓝色和橙色谐振环表示模场谐振环，分别用来激发频率为ω0、ω1的光模式；黑色谐振环表示动态耦合谐振环，具有梯度相位分布，可以在两端分别激发频率为ω0、ω1的光模式，以实现两种模场谐振环的耦合。引入动态调制的人工频率可以理解为态平面之间形成了“螺位错线”，由于螺位错线的存在，在光子带隙中产生了沿人工频率传播的拓扑保护态，如图7(d)所示。

该工作通过合成维度对二维谐振环的拓扑设计，实现了从二维拓扑光子态到三维拓扑光子态的扩展，且拓扑光子带隙可调，为研究晶格缺陷与能带拓扑结构的相互作用提供了思路，同时为研究三维拓扑光子态的特性提供了新方法。该调制方案可应用在三维拓扑绝缘体中具有鲁棒性的单向传输波导的情况，实现对输入信号的单向频率转换的功能。

对比上述两个合成维度拓扑工作，其共同点为均采用二维平面谐振环结构以产生三维结构体中的拓扑保护模式，且实现了拓扑保护模式的单向频率转换。二者存在的不同点如下：前者采用六边形排布谐振环结构，且对每一个谐振环进行调制，通过改变每一个谐振环的等效折射率分布以实现不同对称性；后者采用正方形排布谐振环结构，通过引入一列动态耦合谐振环，可以在人工频率轴上形成“螺位错”，从而实现了频率的连续变化。相较而言，后者只需精确调控动态耦合谐振环的调制相位即可实现相应人工控制，调控区域更小且精度更高，是一种更优选的人工调制模式。

5 总结与展望

近年来拓扑光子学领域的蓬勃发展，已经使这个领域成为了物理学与光子学领域的前沿。拓扑光子学起源于凝聚态物理，但又有所不同，与电子系统相比，光子系统有着更灵活的结构设计和调控方式，使得在电子系统中难以实现的物理模型成为现实可能，可以作为验证凝聚态最新理论的平台。虽然目前一维、二维、三维的拓扑光子学结构已经被设计并制备出来，光学拓扑超材料领域依然面临一些挑战。

首先，目前研究的拓扑结构大部分是厄米（Hermitian）系统，在实际光学结构中，大都是具有开放边界、有增益、损耗分布的非厄米（non-Hermitian）系统，研究非厄米光学与拓扑光子学的相互作用对于光学拓扑结构的实际应用至关重要[72]。不同于在厄米系统中存在的狄拉克简并点，非厄米系统的复频谱中存在的简并点被称为奇异点（Exceptional Point，EP），在EP 点，光学系统的本征模式会出现合并。通过构建系统的增益损耗分布，可以通过EP点获得系统从PT（Paritytime）对称相到PT 非对称相的转变，在PT非对称相可以获得对特定光学模式的增益。非厄米光学和拓扑光子学有着一定的重合，通过在非厄米系统中构建拓扑非平凡的光学结构，可以把拓扑光子学和非厄米光学结合起来，通过非厄米特性和拓扑光子学的相互作用，可以获得很多不同于厄米系统中的奇特的物理现象，这将极大地扩展拓扑光子学的应用。

其次，对于高阶拓扑的研究给了拓扑光子学新的机遇[73-78]。如果一个N维的拓扑光子系统可以支持N-m维度的边界态,称为m阶拓扑绝缘体，当m大于1时，这种拓扑绝缘体具有高阶拓扑效应。目前已经有多篇工作在二维光子结构中实现了零维角态，最近北京理工大学Weixuan Zhang等人设计的一种二维光子晶体微腔具有高阶拓扑相，可以支持零维的角态，以此为基础制备出了具有高品质因子和小模式体积的拓扑激光器[76]。高阶拓扑绝缘体为实现具有拓扑保护的光学局域态调控提供了新的研究思路。

目前拓扑光子器件的可协调性需要加强。目前设计制备的光学拓扑结构缺乏可调性，一旦加工制备完毕，对应拓扑边界态的频率也就固定了，无法进一步调节。通过光学拓扑超材料与光学性质可调材料耦合，实现带隙调节，拓扑态频率的调节或开关切换，构建具有主动可调功能的光学拓扑结构，将极大地拓展光学拓扑结构的实际应用范围。