二维光子拓扑绝缘体研究进展

刘 慧，王好南，谢博阳，程 化*，田建国，陈树琪,2,3*

（1. 南开大学 物理科学学院，泰达应用物理研究院，弱光非线性光子学教育部重点实验室，天津 300071；2.山西大学极端光学协同创新中心，山西太原 030006；3.山东师范大学光场调控及应用协同创新中心，济南 250358）

1 引 言

拓扑学是十九世纪形成的数学领域的一个重要分支，主要研究几何图形或空间在连续形变下的不变性质[1]。凝聚态物理中整数量子霍尔效应的惊人发现赋予了拓扑学全新的物理意义，由此拓扑物理学作为一个新兴的领域得到了人们的广泛关注。1980年，Klitzing发现在强垂直磁场中的二维电子气体具有量子化的霍尔电导[2]，这种量子化的霍尔电导不受样品大小，杂质和成分的影响，精确度高达十亿分之一。1982年，Thouless等人意识到量子化的霍尔电导来源于能带的非平庸拓扑性质，这就是著名的Thouless、Kohmoto、Nightingale和den Nijs (TKNN)的理论工作[3]，其拓扑不变量以第一陈数来表征。体边对应原则（bulk-edge correspondence principle）进一步诠释了拓扑不变量的物理意义：当两种具有不同拓扑不变量的材料相接触时，在拓扑带隙频率下，两材料界面处必然存在空间局部化的边界态。除非带隙关闭，系统的拓扑不变量在扰动或变形下保持不变，因此拓扑保护的边界态可以不受材料缺陷和杂质的影响，从而实现边界态的鲁棒传输。意识到拓扑的概念广泛存在于波动系统后，Haldane和Raghu 首次创造性地将拓扑的概念引入光子晶体[4-5]，利用磁光材料打破时间反演对称性(time-reversal symmetry)，他们在二维光子晶体中构造出了陈数非零的拓扑绝缘体，得到了单重拓扑保护的边界态，该光量子整数霍尔效应的理论方案不久被Wang 等人在微波频段设计[6]并在实验上得到证实[7]。这样的光学材料被称为光拓扑陈绝缘体，与电子系统陈绝缘体内部绝缘而表面导电类似，其内部不透光而表面却存在单重拓扑保护的表面模式，这样的表面态可实现光对材料杂质缺陷免疫的无损耗传播，这是前所未有的理想传输特性，可以克服传统光学器件对材料杂质缺陷产生强损耗的缺点，有望驱动新型光学器件的变革[8-13]。与时间反演对称性破缺的拓扑物理相关的设计概念也在其他周期系统中实现，如声子晶体[14-15]、冷原子体系[16-18]和经典机械波系统[19-21]。

上述光整数量子霍尔效应依赖于微波频率下旋磁材料的磁光效应，存在外加磁场影响光学器件集成、频率局限于微波频域无法推广到光学频率和现有旋磁材料对磁场的响应较弱等问题，这大大限制了拓扑陈绝缘体在光学器件的应用。凝聚态HgTe量子阱中量子自旋霍尔效应的发现提供了另一种无需打破时间反演对称性就能实现拓扑边界态的方法[22-25]。对于缺乏自旋内禀自由度的系统，为了构造一个类Kramers简并，赝自旋被引入光学系统。在不打破时间反演对称性下，每个赝自旋受到相反的人工磁场的作用，此时系统的陈数为零，但自旋陈数不为零。这种基于量子自旋霍尔效应的拓扑绝缘体内部是绝缘的，在两个具有不同自旋陈数的材料界面处，激发拓扑带隙频率可观察到一对传播方向相反的螺旋拓扑边界态。双各向异性超材料、环形谐振腔光波导[26-27]、点群对称性保护的光子晶体[28-30]、拓扑射频电路[31]等多种光系统中均提出了量子自旋霍尔效应的方案，极大地促进了拓扑光子学的发展。除此之外，引入人工合成的有效规范势和有效磁场代替外加磁场的方案相继被提出。其中较为典型的是光Floquet 拓扑绝缘体[32-38]，在有效哈密顿量中加入周期性的时间调制，利用光相位动态调制打破时间反演对称性，产生有效规范势和人工合成的磁场。研究人员基于光Floquet 拓扑绝缘体展开了许多有趣的研究，如非线性自局域态[39]、不成对狄拉克锥[40]等。类似地，在有效哈密顿量中加入时间相关的调制，拓扑泵在准晶体系中得以实现[41-44]。有趣的是这种准晶体系能实现更高维度的非平庸拓扑特性，例如在一维拓扑泵中，一维准晶拥有二维的陈数，并出现与二维量子霍尔效应边缘态等价的拓扑保护边界态。近年，一种突破体边对应原则的拓扑绝缘体被提出，称为高阶拓扑绝缘体[45-50]，其对应的高阶拓扑态，如角态和棱态，受到越来越多的关注。

随着拓扑物理研究的深入，电子系统暴露出能带结构复杂难以得到干净的带隙，材料缺陷和杂质难以控制和拓扑描述所需的单电子近似失效等问题，因此，研究人员逐渐将目光投往其他经典系统中，例如光子系统，声学系统[51–56]和机械系统[19,57]。光学系统作为经典的玻色子系统，具有能带相对干净，样品设计简单和样品制作精度较高等优势，逐渐成为拓扑物理研究的重要平台，由此催生了光学领域许多研究方向。二维拓扑绝缘体的研究被扩展到三维领域，时间反演对称性破缺[58]和时间反演对称保留[59-61]的三维拓扑绝缘体分别被实现。被称为拓扑半金属的无带隙拓扑相在三维光子晶体中得到实现[62-65]，此时费米能级被频率所替代，调节频率可以实现能带内任意频率体态和费米弧的激发和测量。通过在系统中引入合成维度，加上自身的空间维度可以探索高于系统本身几何尺寸维度的物理内容[66-71]。比如可以在一维结构中构建参数空间[72]、二维环形谐振腔阵列中合成频率维度[73]，实现对外尔点的调控[74-76]。在合成空间中不仅能表现丰富的拓扑物理性质，也多了新的方法去控制光。非线性光学介质与拓扑物理结合得到了许多有趣的发现，如在光子拓扑绝缘子里的孤子[77-78]、自诱导拓扑跃迁[39,79]和强相关光子态[80-82]。当考虑光学材料的增益和损耗时，有效哈密顿量是非厄密的，这种非厄米系统的拓扑特性逐渐受到人们的关注[83-85]。

本文基于二维光子系统，介绍了几类受广泛关注的拓扑绝缘体。首先介绍了以光整数量子霍尔效应和光量子自旋霍尔效应为代表的两种类型的拓扑绝缘体，以及它们在光子晶体、耦合波导和超材料中的实现。值得注意的是上述两种拓扑绝缘体前者时间反演对称性破缺且依赖于光学材料对磁场的响应，后者无需施加磁场故时间反演对称性得到保留，两者属于不同的拓扑分类，前者拓扑性质用陈数描述，后者用自旋陈数描述。然后，我们讨论了时间相关调制的Floquet 拓扑绝缘体，它在无需施加磁场的情况下打破时间反演对称性。与光整数量子霍尔效应不同，虽同为时间反演对称性破缺的拓扑绝缘体，Floquet 拓扑绝缘体无需施加磁场，弥补了光整数量子霍尔效应依靠光学材料对磁场的响应，仅能实现微波波段的鲁棒传输的缺陷，实现了光学频段内的鲁棒传输。随后，介绍了基于上述几种传统拓扑绝缘体设计的由无序驱动产生的拓扑安德森绝缘体以及突破传统的体边界对应原则的高阶拓扑绝缘体。文章的最后对光学拓扑前沿领域的发展进行了总结和展望。

2 二维光整数量子霍尔效应

随着电子系统拓扑相研究的深入，人们逐渐认识到拓扑的概念广泛地存在于不同的物理系统中。受凝聚态二维电子气系统研究的启发，Haldane和Raghu 基于无质量Dirac方程首次提出了光整数量子霍尔效应方案[4]。在二维周期系统，Dirac 锥在布里渊区受到时间反演对称性保护从而形成二维平面上的简并点。Dirac点成对产生或湮灭，在动量空间两条能带之间形成线性色散，其附近准粒子特性可用有效哈密顿量H描述：

其中F(k)=∇k×A(k)为贝利曲率（Berry curvature），A(k)=〈u(k)|i∇k|u(k)〉为贝利联络（Berry connection）。二维的布里渊区是可以上下左右连接在一起得到一个环面。陈数可以看作环面内贝利通量(Berry flux)单极子的数量。这里的贝利联络可以类比实空间电磁场中的矢势，贝利联络沿闭合回路积分得到贝利相位(Berry phase)，矢势沿闭合回路积分得到AB相位(Aharonov-Bohn phase），贝利曲率类比磁场中的磁场B(r)，贝利曲率的通量类比磁场通量，贝利曲率在布里渊区上的积分得到陈数，类比磁场中磁单极子数量，这些物理量都是可以一一类比的。

Haldane和Raghu 的理论预测很快在微波波段得到实现[89-91]。2008年，Wang 等人意识到构造Dirac点能带结构并不是实现光量子整数霍尔效应的必要条件，他们利用钇铁石榴石的磁光效应，在四方晶格能带的交会点附近打开带隙，构造出了第一陈数非零的拓扑绝缘体。基于这种更为普适的方案[6]，2009年他们首次在微波频段实现了光整数量子霍尔效应，在旋磁铁氧体棒组成的光子晶体中观测到了背散射免疫的单向传输边界态[7]。光整数量子霍尔效应实验装置如图1(a)所示，空气中的旋磁铁氧体棒和金属板组成了二维四方格子光子晶体。如图1(b)所示，外加一个垂直平面的磁场，系统的时间反演对称性被打破，出现的背散射抑制的单向传输边界态可绕过四方晶格中的障碍物传输。根据体边对应原则，上述陈数为1的拓扑绝缘体带隙中只有一条单向背散射免疫的边界态，若想获得多重拓扑保护的边界态则需要构造更高陈数的拓扑绝缘体。Skirlo等人理论上提出基于二维铁磁性光子晶体，在外加磁场的作用下同时打破Dirac点和非线性简并点，可以实现高陈数的拓扑绝缘体，从而获得多重拓扑保护的边界态[89]。高陈数的拓扑绝缘体随后被实验所证实，二维铁磁性光子晶体的理论与实验拓扑带隙图分别如图1(c)、1(d)所示，显示出高拓扑陈数与频率和外加磁场的函数关系[90]。根据拓扑带隙图施加外加磁场，得到带隙陈数分别为+1，+2，−3和−4的拓扑绝缘体，在对应频率下观测到一条、二条、三条和四条单向拓扑保护的边界态，实验和理论结果分别如图1(e)、1(f)所示。

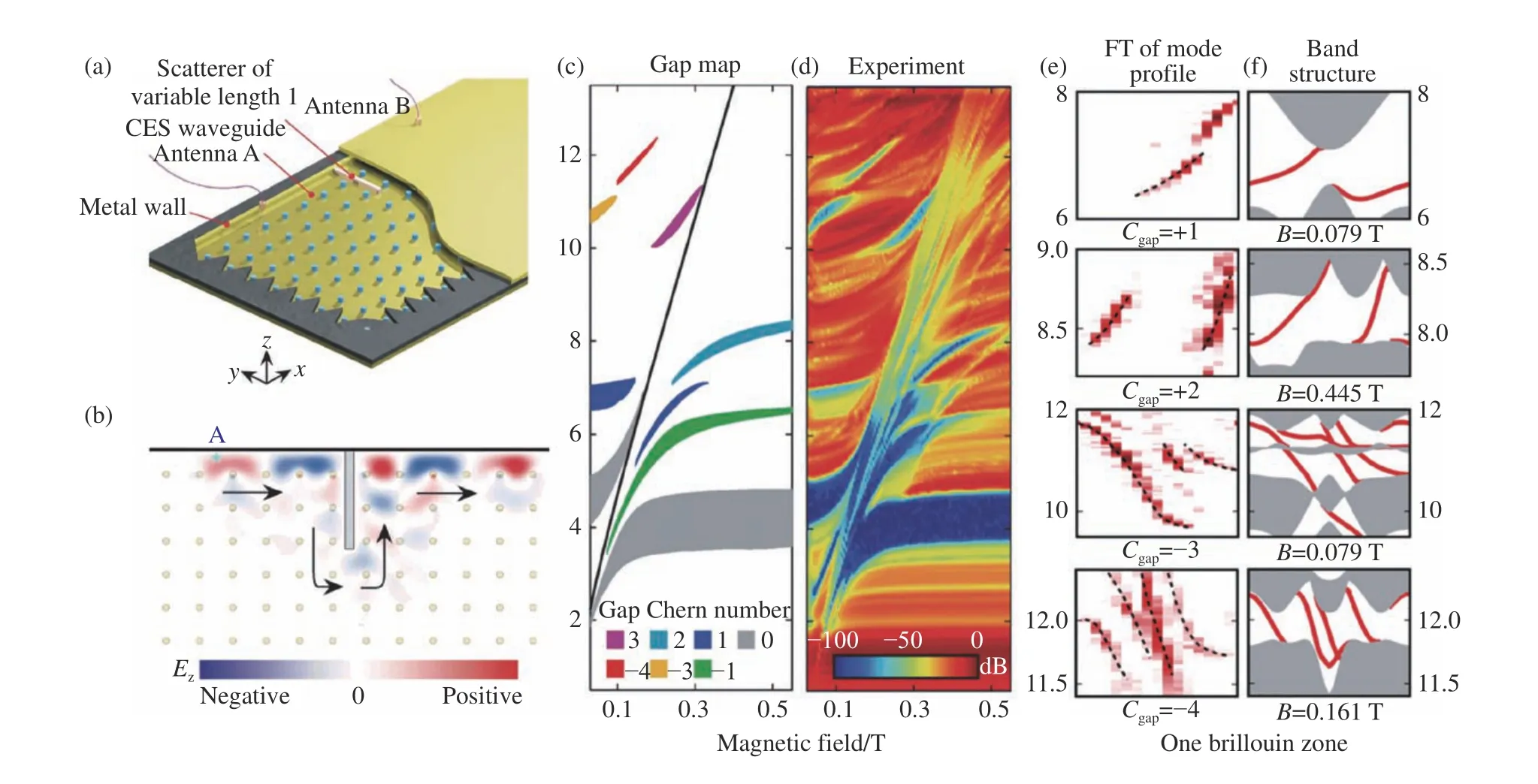
图1 (a)由旋磁铁氧体棒和金属壁组成的二维光整数量子霍尔效应的实验装置图[7]。(b)在垂直方向磁场作用下，模拟手性边缘态绕障碍物周围的传播示意图[7]。(c)以磁场和频率为函数的理论拓扑带隙图，其中每个带隙的拓扑不变量用带隙陈数标记[91]。(d)实验测量的拓扑带隙图[91]。(e)和(f)分别表示不同陈数的边缘态实验和理论的示意图[91]，其中灰色部分为体带，红色线表示边缘态。Fig.1 (a)Experimental setup of 2D optical integer quantum Hall effect consisting of gyromagnetic ferrite rods and metal walls[7].(b)Simulated propagation of chiral edge states around obstacles in the presence of a vertical magnetic field[7].(c)Theoretical topological gap map as a function of the magnetic field and the frequency,in which the topological invariants of each band gaps are labeled by its gap Chern number[91].(d)Experimental topological gap map[91].(e)and(f)represent the schematic of experimental and theoretical edge states with different gap Chern numbers[91], respectively,in which gray part is bulk bands and the red lines represent the edge states.

时间反演对称性破缺的拓扑陈绝缘体已在光学领域内展开了广泛的研究，其单向背散射免疫边界态是传统光学器件不具备的理想传输态，这种理想的传输态极大地启发了新型光学器件的设计，包括慢光波导[91]、拓扑太赫兹电路[12]、定向过滤器[92]、磁控制波导器件[8]、光拉力[93]等。然而，不同于电子对磁场的强响应，光学系统中打破时间反演对称性依赖于光学材料对磁场的响应，由于现有的光学材料的磁响应较弱且磁响应频率范围局限以及外加磁场对器件集成的不利影响，拓扑陈绝缘体在光学器件中的应用仍然是一个挑战。

3 二维光量子自旋霍尔效应

二维拓扑光子系统的另一大类是保留时间反转对称性的系统，类似于凝聚态中的量子自旋霍尔系统[24-25]和量子谷霍尔系统[94-95]。谷是指动量空间能带结构的两个极值处，因为上下谷的贝利曲率符号相反，所以在布里渊区上的积分和等于零，然而每一个谷在布里渊区上的积分却不等于零。因为总陈数为零，所以该系统的时间反演对称性是保留的。谷自由度作为潜在的信息传递载体，在经典波系统也引起了广泛的关注，已经在光子系统[96-100]和声学系统[101-103]中实现了类量子谷霍尔效应。二维光量子自旋霍尔效应的实现不依赖于外加磁场和光学材料的磁响应，拓扑保护的边界态在光学频段得以实现，这更有利于光学新型器件的设计和应用。对于保留时间反演对称性的系统，非简并带贝利曲率遵循 Ωn(−k)=−Ωn(k)，这意味着贝利曲率在整个布里渊区的积分为零，也就是陈数为零，此时陈数已不能描述系统的拓扑不变量。量子自旋霍尔效应首先在电子系统中实现，电子拥有自旋向上和自旋向下的内禀自由度，每个具有自旋向上或自旋向下的能带都可以通过式(2)用拓扑不变量C+或C−来描述，两者满足关系C+=−C−，此时体系的陈数C=(C++C−)/2为零。定义自旋陈数描述保留时间反演对称性系统的拓扑不变量：Cs=(C+−C−)/2，这与电子Z2绝缘体的情况类似，两个自旋态中存在数量相同但传播方向相反的边界态，这种非手性的边界态被称为螺旋态。不同于电子这样自旋为1/2的费米子系统，光子作为玻色子自旋为1，缺乏固有的双重简并，也就是Kramers简并。根据Kramers理论，量子自旋霍尔效应需要系统满足时间反演操作算符T2=−1，电子作为费米子，其时间反演操作算符恰好满足这一要求，而光子作为玻色子，其时间反演操作算符却遵循T2=+1。为了消除玻色子固有属性的影响，将赝自旋和赝时间反演操作T2=−1引入光学系统中，由此构造出与Kramers类似的简并。对于缺乏Kramers简并的无自旋体系，如光子、声学和力学，可以构造一对赝自旋向上和赝自旋向下的共轭态。在一定人工规范对称性的保护下，可以存在类Kramers简并，从而实现量子自旋霍尔效应。下面介绍几种光学系统中构造赝自旋以实现光自旋霍尔效应的方法。

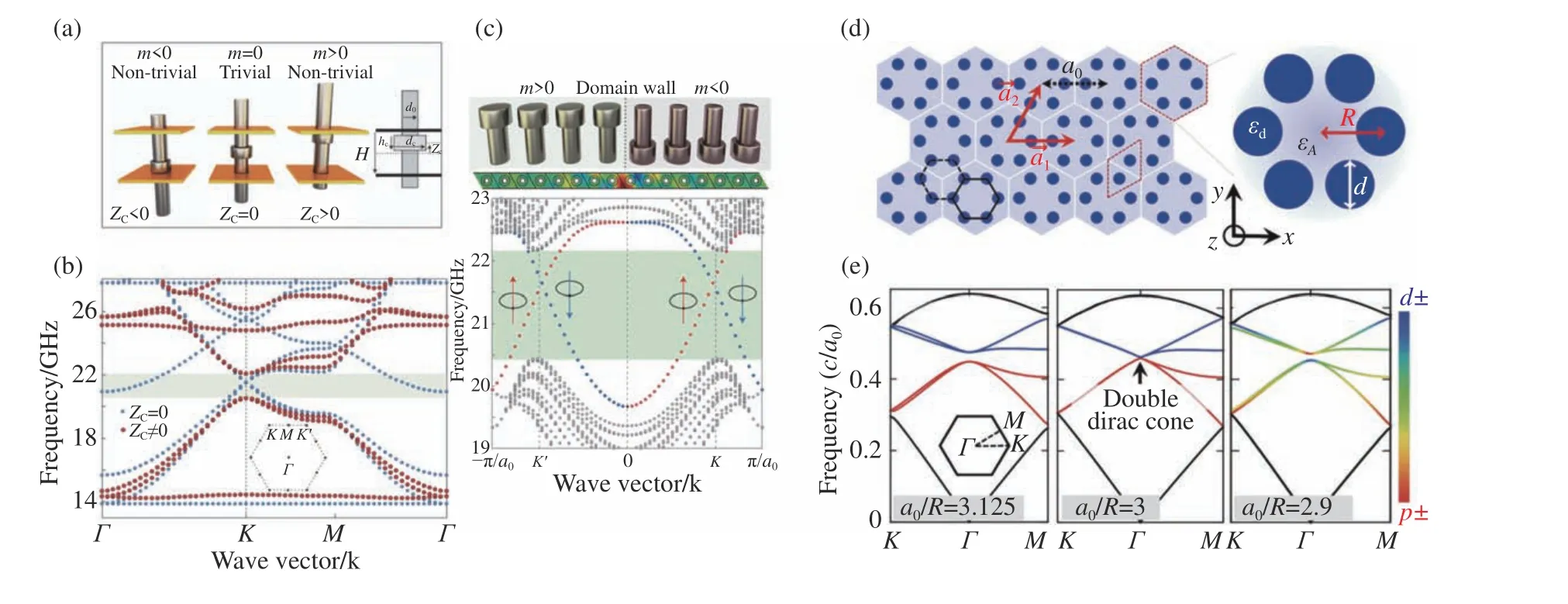
Khanikaev 等人理论上提出了一种基于双各向异性材料，利用光的TE和TM 偏振自由度实现光量子自旋霍尔效应的方法。他们在由电磁介质组成的六方晶格超晶体中，设计介质的有效介电常数与磁导率相等（ε =µ），迫使TE+TM和TE-TM两个赝自旋态形成类Kramers简并，通过控制材料的电磁耦合实现类Kramers简并闭合和打开，由此实现二维光量子自旋霍尔效应[104]。研究表明，超晶的界面存在与电子拓扑绝缘体类似的一对自旋依赖的螺旋边态，这使光子在无外加磁场的情况下实现单向传播成为可能。然而，上述方法需要超材料中的有效介电常数与磁导率严格相等，由于天然材料对电场分量和磁场分量的响应不同，在实验中很难实现有效介电常数与磁导率相等的严苛条件。最近，无需材料有效介电常数与磁导率严格相等的结构方案被提出[105-108]。基于石墨烯格子的晶格对称性，精心设计金属柱体和环的几何结构，将环置于两板之间，光的TE和TM 模式在布里渊区的K（K’）点形成简并的Dirac锥对[107]。双各向异性是通过移动圆柱体上的环来实现的，如图2(a)所示，通过向上或向下滑动金属环来破坏 σz的对称性会产生类似自旋轨道耦合效应，从而在有效哈密顿量中引入一个有效质量项m。如图2(b)所示，滑动金属环引入双各向异性，体带在高对称点处的简并点实现闭合和打开，系统发生拓扑相变从而出现拓扑非平庸的带隙。两个具有相反有效质量的晶体界面处存在一对传输方向相反的赝自旋依赖的界面态，如图2(c)所示，这对拓扑保护的界面态在实验中显示出背散射抑制的特性。

Wu 和Hu 提出利用晶格对称性实现光量子自旋霍尔效应的方案[28]。二维光子晶体原胞由6个电介质材质的圆柱体组成，如图2(d)所示。基于带折叠机制，石墨烯晶格布里渊区的K点和K’点处的Dirac锥被折叠在 Γ点处形成双Dirac锥，简并的布洛赫模式杂化形成一对赝自旋态。通过拉伸或压缩人造原子间的距离，双重简并Dirac锥被退简并得到一个拓扑平庸或非平庸带隙，带隙的闭合和打开导致p和d带之间发生带反转，系统实现拓扑相变，如图2(e)所示。此时，在非平庸光子晶体(图2(e)右)和平庸光子晶体(图2(e)左)的界面处出现一对拓扑保护的赝自旋依赖的螺旋边界态。与其他方案相比，这种依赖晶格对称性构造类Kramers简并的方案让光量子自旋霍尔效应在传统的电介质材料中得以实现，简单的结构设计使其在实验中更容易实现，深刻的影响着拓扑物理在声学系统[53,109]、超表面[110]和光子量子等领域[111]的研究。

Hafezi等人提出了耦合环谐振器方案[26-27]。通过控制光沿环形谐振腔顺时针和逆时针的路径，在系统中构造了一对顺时针和逆时针方向的赝自旋简并态。同时，光沿晶格单元顺时针或逆时针传播会引入相反的有效规范势，一对赝自旋态感受到相反的有效磁场，由此光子的有效磁场就在这个非磁性系统中合成了，光量子自旋霍尔效应得以实现。该方案在二维硅光子平台实现，光学耦合环谐振器如图2(f)所示[27]，连接谐振器将位置谐振器相连接，由此形成二维周期耦合阵列。实验在非平庸带隙激发了一对拓扑保护的螺旋边缘态，如图2(g)所示，调整激发频率可选择激发不同自旋依赖的螺旋边缘态。

Jia 等人提出了射频光子电路的方案[31]。将赝自旋态编码在晶格的两个等效电感A 和B中，两个电感通过耦合原件实现电容耦合，电容耦合电感网络和耦合原件分别如图2(h)、2(i)所示。考虑图2(h)中一个光子由A 电感绕一个方格的拓扑耦合（黄色箭头），耦合过程产生了−π/2的贝利（Berry）相位，这样就在方格的排列耦合中合成了射频光子自旋相关的有效规范场。如图2(k)所示，光子射频电路中体态密度和边缘态密度的测量是射频绝缘体带和导电边缘态存在的证据。实验样品如图2(j)所示，激发其体带并测量其体带态密度，体带态密度图呈现一段体态密度极小的带隙，如图2(k)左图所示。选取位于带隙频率之间的频率激发样品边缘处，测量样品边界态密度观察到射频电路导电边缘态如图2(k)右图所示。这种基于拓扑电路的方案设计简单，被应用于拓扑角态[112]、Weyl半金属[113-114]以及强耦合[115]等拓扑物理的研究中。

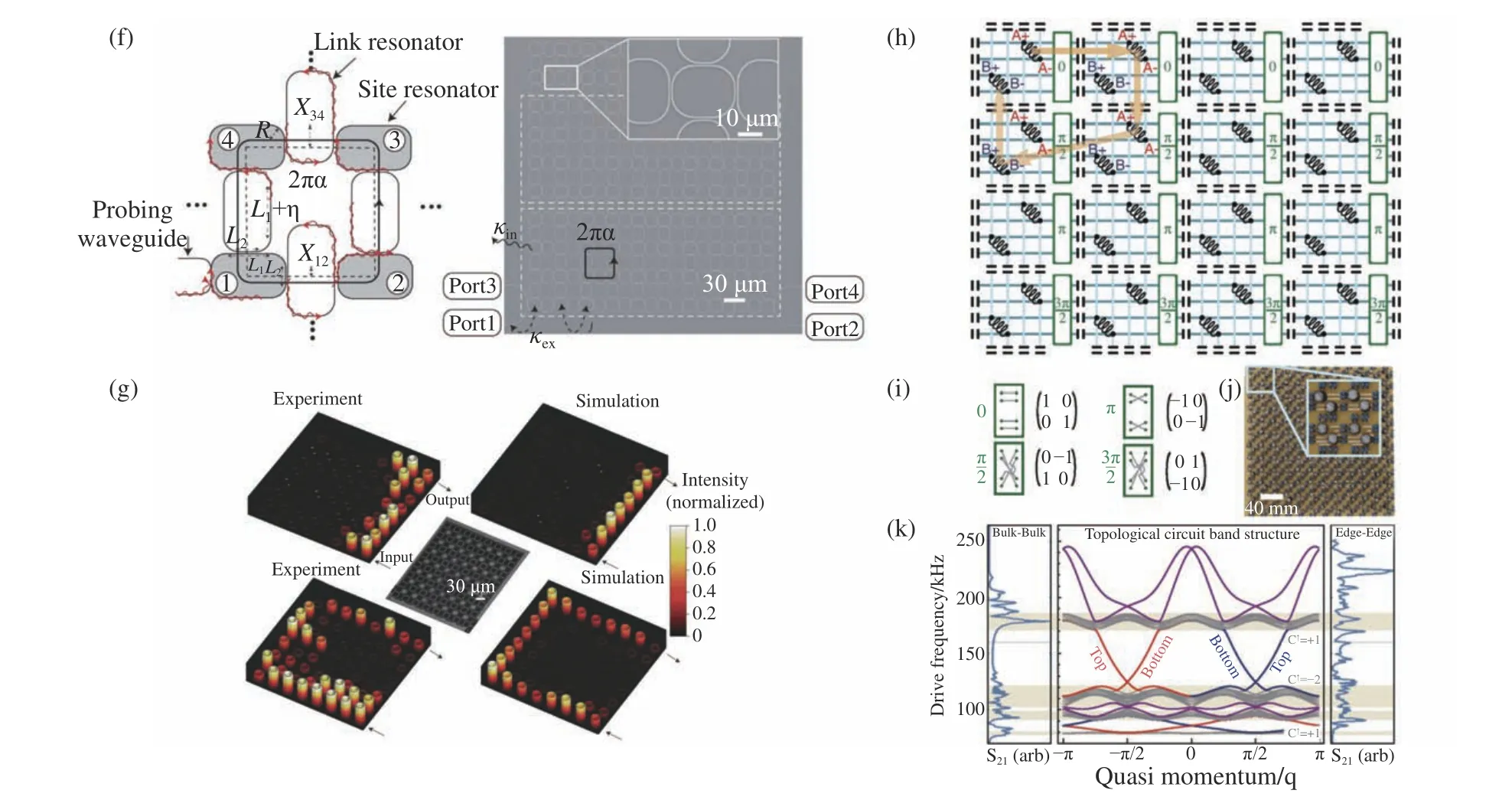
图2 (a)可重构拓扑超晶的设计示意图[107]。移动金属环与金属板的相对位置可在简并处引入负的(左)、零(中)或正的(右)有效质量。(b)可重构拓扑超晶的体带示意图[107]，其中蓝色点线和红色点线分别对应对称(无双各向异性)和非对称(有双各向异性)结构。(c)有效质量相反的两种超晶结构的界面及相应的边带图[107]。(d)基于六角晶格的二维电介质光子晶体示意图[28]。(e)改变人工原子之间的距离，将 a0/R的比值设定为3.125(左)、3(中)、2.9(右)的二维光子晶体能带结构，其中彩色能带展现了能带杂化[28]。(f)由位置谐振器和连接谐振器组成的光学耦合环谐振器单元(左)及其组成的二维硅光子平台的实验装置图(右)[27]。(g)不同激励频率下实验(左)和模拟(右)的边缘态示意图[27]。(h)射频电路拓扑绝缘体示意图，周期结构由位置电感器和耦合电容组成[31]。(i)格点间耦合元件结构[31]。(j)射频电路拓扑绝缘体实验样品图[31]。(k)射频电路的理论能带结构(中)，实验测量的体态密度(左)和边缘态密度(右)[31]。Fig.2 (a)Schematic of reconfigurable topological metacrystal[107].Moving the relative position of the metal ring to the metal plate introduces negative(left),zero(middle),or positive(right)effective masses at the degeneracy.(b)Bulk band structures of reconfigurable topological metacrystal[107],in which blue dotted line and red dotted line correspond to symmetric(no bianisotropy)and asymmetric(with bianisotropy)structures, respectively.(c)The interface of two metacrystal structures with opposite effective masses and the corresponding edge band diagrams[107].(d)Schematic of 2D dielectric photonic crystal of honeycomb lattice[28].(e)The band structure of 2D photonic crystals with a0/Rratios of 3.125(left),3(middle),and 2.9(right)was set by changing the distance between the artificial atoms where the rainbow for band hybridization[28].(f)The unit of 2D coupled optical-ring resonators with site resonators and link resonators(left)and the experimental setup diagram of 2D silicon photonic platform(right)[27].(g)Schematic of edge states of experiment(left)and simulation(right)at different excited frequency[27].(h)Schematic of radio-frequency(RF)circuit topological insulators in which the periodic structure consists of position inductor and coupling capacitor[31].(i)Structure of the coupling elements between lattice sites[31].(j)Sample diagram of radio-frequency(RF)circuit topological insulators[31].(k)Theoretical band structure of RFcircuit(middle).Experimental density of states of bulk state(left)and edge state (right)[31].

4 光Floquet 拓扑绝缘体

4.1 陈Floquet 拓扑绝缘体

Floquet 拓扑绝 缘体在‘高频’范 围时[32-33]，微观运动是不重要的，系统有效哈密顿量可以通过陈数描述。2013年，Rechtsman,M.C.等人在图3(b)的螺旋形波导阵列中，在光波段实验实现了Floquet 拓扑绝缘体[34]。其中，近轴光线的传播由一个类似薛定谔方程的式子描述：

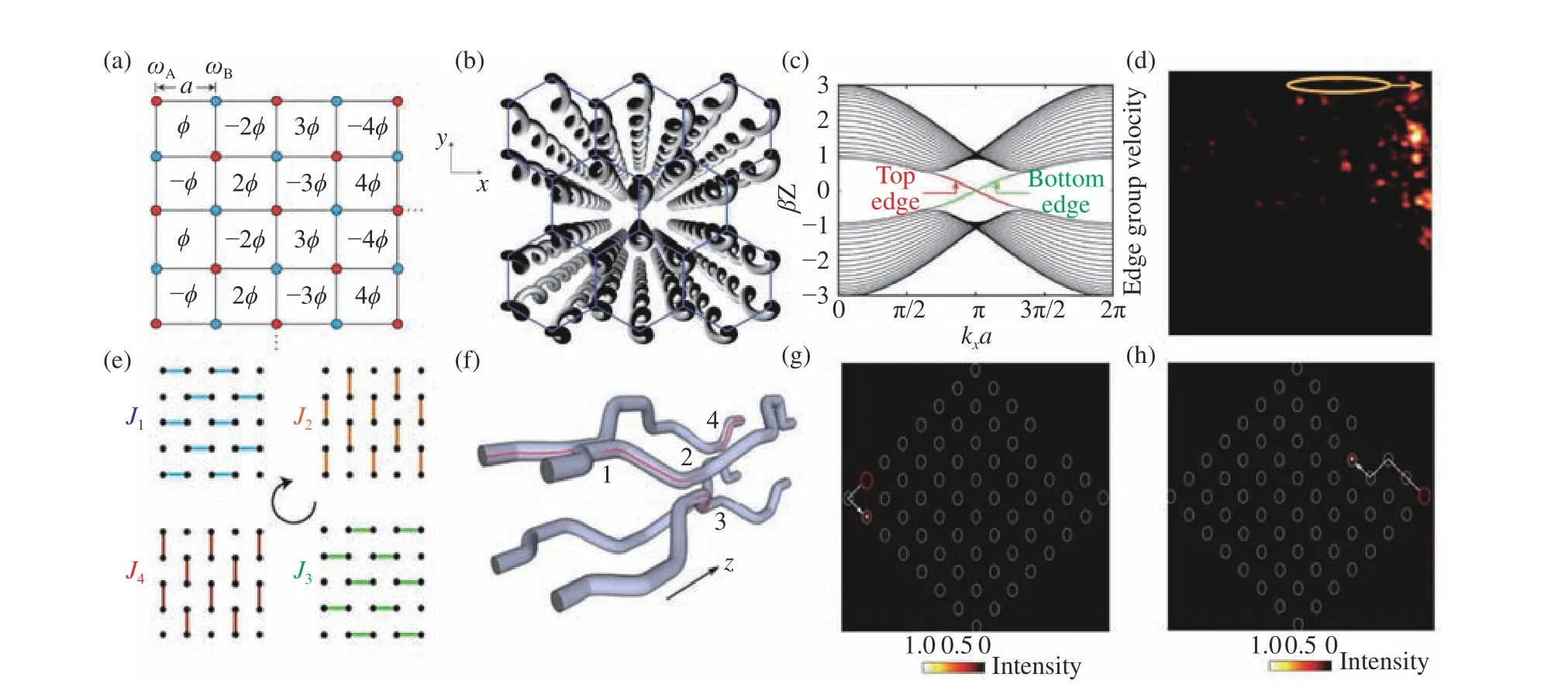
图3 (a)光学谐振腔阵列动态调控产生的有效磁场[118]。(b)通过激光直写技术制作的螺旋波导阵列[34]。(c)螺旋波导R=8μm的投影能带图[34]。(d)实验测量的出射面光强分布图，黄色的椭圆代表输入光束位置[34]。(e)一个传播周期内4种不同的耦合方式(J1-J4)[37]。(f)精心设计的波导结构示意图，传播方向z 轴和时间轴等价[37]。(g-h)场强分布的实验测量图，不被拐角(g)和缺陷(h)散射的手性边界态[37]。Fig.3 (a)Effective magnetic field generated by dynamic control of photonic cavity array[118].(b)Helical waveguide array made by laser direct writing technology[34].(c)Projected band diagram of spiral waveguide R=8μm[34].(d)The experimentally measured light intensity distribution of the output facet, the yellow ellipse shows the position of the input beam[34].(e)Four different coupling modes(J1-J4)in one propagation cycle[37].(f)Schematic diagram of finely engineered waveguidestructure,the propagation direction z axis and time axisareequivalent[37].(g-h)Experimental measurement diagram of field intensity distribution,chiral edge states that are not scattered by corners (g)and defects (h)[37].

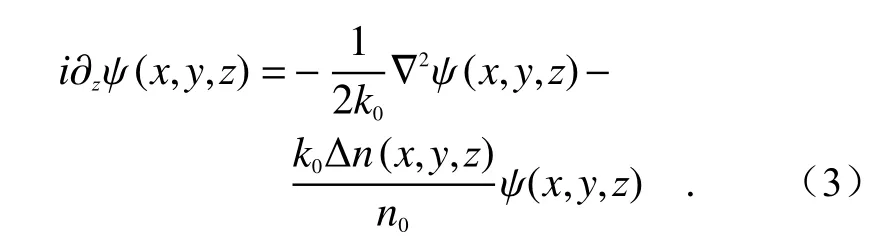
这里ψ(x,y,z)是 电场的包络函数，k0是介质中的波数。当光沿z方向传播时，其在螺旋形波导阵列中的传播类似电子随原子在二维晶格中旋转运动的时间演化。当螺旋半径R=0 时，系统的能带简并形成类似石墨烯的狄拉克锥。当螺旋半径R>0，简并点打开形成一个带隙，在带隙中间存在拓扑保护的边界态，如图3(c)所示。从输出面的光强分布来看,从晶格出射的光束被限制在边缘，没有扩散到整个空间，并且没有任何反向散射，如图3(d)所示。这里把空间的z轴看作时间轴，相比含时的周期性调制，调节更容易，为探索Floquet 相提供了一个新思路。

4.2 反常Floquet 拓扑绝缘体

若Floquet 拓扑绝缘体突破‘高频’限制，在‘低频’范围时，微观运动作用不能忽略，则不能用陈数完全描述，而是用绕数(winding numbers)来表征体系的拓扑性质[35-36]，此时称反常Floquet 拓扑绝缘体[119]。2017年，Mukherjee和Maczewsky 用波导阵列在一个周期内引入4种耦合方式，分别实验观察到了拓扑保护的手性边界态[37-38]。如图3(e)所示，J1到J4这4种耦合以空间均匀时间周期的方式变化，所以每个晶格格点在任何时刻都仅耦合到其最近邻的一个格点上。通过精心设计4个波导结构在z方向上的空间位置，可以实现这4种不同的耦合，如图3(f)。在这个波导阵列结构中，传播方向z轴扮演着时间的角色。实验测量输出界面的场强分布，观察到了不被拐角散射和对缺陷免疫的手性边界态，分别如图3(g)和图3(h)所示，表明这些边界态是受拓扑保护的。两个实验小组都观察到了上述反常Floquet拓扑态，其中手性边界态由非平庸的绕数唯一确定。

光子Floquet 拓扑绝缘体提供了一个探索和理解拓扑相的新平台。除了以上几种途径实现Floquet 拓扑相，其它方案也不断提出，可以应用到不同的物理平台，如准晶类型[41]，网络模型的Floquet 构型[120]，微波范围金属表面等离激元[121]以及周期性驱动的分形晶格[122]等。

5 拓扑安德森绝缘体

无序在拓扑绝缘体中扮演着一个重要角色，对于传统的拓扑绝缘体，拓扑相中的边界态对局部弱无序免疫，但如果无序的强度足够大时边界态会消失。但有一类特殊的拓扑绝缘体，其拓扑保护的边界态是由无序引起，称为拓扑安德森绝缘体[123-124]。拓扑安德森绝缘体，首先由Li等人在HgTe/CdTe量子阱中提出[123]，它们发现随着无序的增加量子化的电导先是消失，超过一定强度之后又会出现。Groth 等人[124]提出的有效介质理论在一定程度上解释了无序产生量子化电导的现象。随着研究的深入，拓扑安德森绝缘体的产生机制逐渐清晰，不论电子或者光子体系，拓扑安德森绝缘体都是基于传统的拓扑绝缘体产生的。因为一些干扰因素的加入，例如失谐和反演对称性破缺，这使得传统的拓扑绝缘体两个高对称点处的有效质量从正负相反变成了都为正的状态，这时候传统的拓扑绝缘体由拓扑非平庸相进入拓扑平庸相，而在此时加入无序可抵消加入的正有效质量的影响，使得系统从拓扑平庸相重新回到拓扑非平庸相之中[124]，这样产生的拓扑安德森绝缘体能与传统的时间反演对称性破缺的绝缘体拥有相同的拓扑性质。根据上述设计机制，多种拓扑安德森绝缘体被设计出来，例如基于Floquet 拓扑绝缘体[125-127]、基于陈拓扑绝缘体[128]、基于自旋陈绝缘体[129-131]、基于高阶拓扑绝缘体[132]的拓扑安德森绝缘体相继被实现。

Stützer 等人首先在二维螺旋波导阵列中基于Floquet 拓扑绝缘体实现了光拓扑安德森绝缘体[127]，实验证明了无序能增强输运而不是抑制输运。波导结构如图4(a)所示，波导阵列通过激光直写技术制作，不同的激光写入速度得到的波导折射率不同，随机改变波导的折射率将引入无序。波导的螺旋会产生一个有效规范势，沿传播方向的反演对称性被打破，可以得到一个拓扑非平庸的带隙。调节使得阵列两个子格子的折射率不同打破中心反演对称性，带隙变成拓扑平庸的，如图4(b)所示。在系统中，无序由 ωri表征，其中ω表示调制参数，ri是−0.5到0.5范围内的随机数，随着调制参数 ω的增加，无序程度增加，拓扑平庸的带隙先闭合然后重新打开，系统转变为拓扑非平庸状态，如图4(c)所示。从图4(d)可以看出，在无序强度足够大时，发生了从拓扑平庸到非平庸的相变，由红色箭头标记。在平庸情况下，光波大部分被反射，如图4(e)所示。加入足够大的无序时，系统进入拓扑非平庸相，光波被局域在二维波导的界面，形成了手性的边界态，如图4(f)所示。此外，Meier,E.J.在一维体系的冷原子链中，构建了动量空间的SSH，证明了该体系从拓扑到非拓扑的转变，和加入无序从非拓扑到拓扑的转变，实现了一维的安德森拓扑绝缘体[137]。二维光波导和一维冷原子中的实验结果为拓扑安德森绝缘体的存在提供了有力的证据。

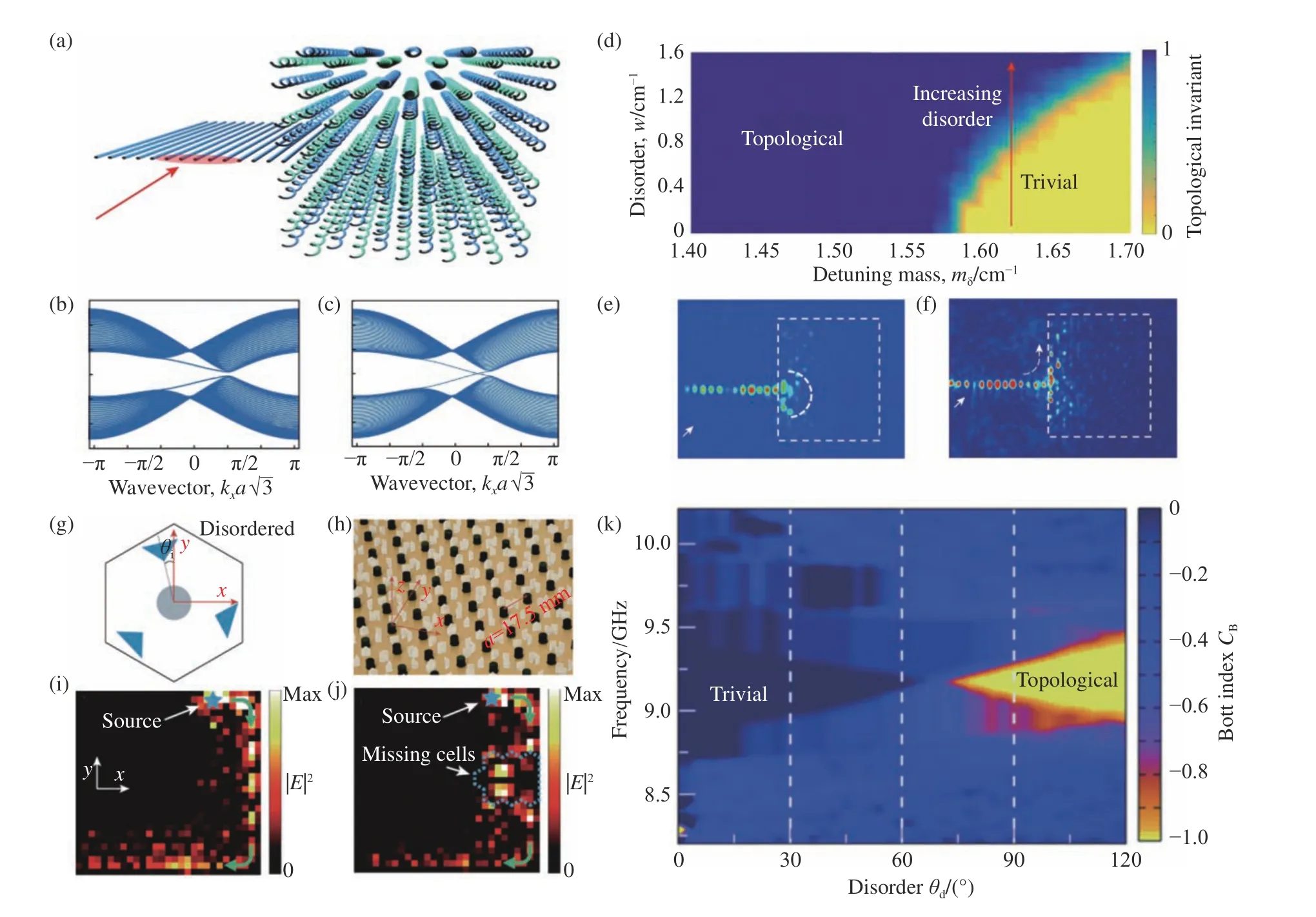
图4 (a)一维波导和螺旋的二维蜂窝波导阵列组成的联合结构[127]。(b)打破中心反演对称性的平庸带隙[127]。(c)添加足够多无序的非平庸带隙[127]。(d)拓扑不变量在无序强度w 和调谐质量m δ共同作用下的相图[127]。(e)处于拓扑非平庸相的实验测量图[127]。(f)加入足够多无序，处于安德森拓扑相的实验测量图[127]。(g)旋转电介质散射体引入无序的示意图[128]。(h)光子晶体的局部图[128]，晶格常数a=17.5 mm。(i-j)场强分布的实验测量图[128]，单向传播(i)和经过缺陷无散射(j)的手性边界态。(k)Bott 因子C B随无序强度变化的模拟图[128]，无序增加，平庸的带隙闭合又重新打开，成为非平庸的带隙。Fig.4 (a)Hybrid structure composed of a one-dimensional straw and a two-dimensional honeycomb lattice of helical waveguides[127].(b)Breaking the parity symmetry of the structure causes a trivial bandgap[127].(c)Sufficiently strong disorder induces a non-trivial bandgap[127].(d)Phase diagram showing the trivial and topological phases as a function of thedetuning mass mδ and disorder strength w[127].(e)Experimental measurement diagram in topological trival phase[127].(f)Add sufficient disorder,experimental measurements in the Anderson topological phase[127].(g)Schematic diagram of disorder introduced by rotating dielectric scatterers[128].(h)Thepartial picture of the photonic crystal,the lattice constant a=17.5 mm[128].(i-j)Experimental measurement diagrams of field intensity distribution[128],chiral edge states that are unidirectional propagation(i)and without scattering(j)through defects.(k)A simulation diagram of the Bott index CB.With increasing disorder strength, the trival band gap closes and reopensas a nontrival band gap[128].

最近，Liu 等人在旋磁圆柱体和三角形的电介质柱构成的二维光子晶体中，基于拓扑陈绝缘体在微波范围实现了拓扑安德森绝缘体[128]。体系的无序是通过随机旋转电介质柱来引入的，由θd Ri表征，其中 θd是调制参数，Ri是−0.5到0.5之间的随机数， θd增大意味着无序程度增大，如图4(g)所示，光子晶体结构如图4(h)所示。为了描述系统的拓扑性质，研究者对拓扑不变量Bott 因子(CB)[133]进行了分析，见图4(k)，模拟了CB随无序强度增大的变化情况，拓扑非平庸带隙出现在无序强度比较大的情况下。加入足够无序时，实验测量到的手性边界态在经过拐角和缺陷时能稳定传输没有明显的损耗，分别如图4(i)和图4(j)所示。该拓扑安德森绝缘体可以直观地理解：在无序不存在时，由于三角形介质柱的存在打破了宇称对称性，抵消了时间反演对称性破缺（导致陈绝缘体）的影响，当旋转三角形电介质引入无序时，宇称对称性的破坏被削弱，又使得陈绝缘体出现。拓扑安德森绝缘体为利用无序作为新的自由度调控边界态提供了一种可能性。

相比于电子系统，光子体系拥有较为干净的带隙且可以更好地控制单原子的在位势能，在光子平台中更容易在原子势能上添加无序，为进一步研究无序在拓扑中的作用提供了更为广阔的平台。无序体系下更丰富的物理现象如三维中无序引起的拓扑相变[138]，无序引起的非线性效应[139-140]，无序的拓扑激光器[141-142]，非厄米系统[143-144]等相继在光学体系中得到实现。

6 高阶拓扑绝缘体

拓扑绝缘体一个显著的特征是具有拓扑保护的边界态，m维的拓扑绝缘体根据体边对应原则[145-146]在界面处具有m−1维的无能隙的边界态。在2017年，研究人员提出了一类突破体边对应原则的拓扑绝缘体，称做高阶拓扑绝缘体[147-148]。这类拓扑绝缘体在界面处有更低维度的边界态，比如m维的n阶拓扑绝缘体，具有m−1,m−2,···,m−n+1维有能隙的边界态，m−n维的无能隙边界态。如在三维体系中，二阶拓扑绝缘体具有棱态，三阶的拓扑绝缘体具有角态，二维的体系中，零维的角态出现在二阶拓扑绝缘体中。

6.1 量子化四极拓扑绝缘体

Benalcazar,Bernevig 和Hughes在多极矩展开时，提出量子多极矩绝缘体模型[45]，并进行了系统的总结[46]。四极矩绝缘体的偶极矩为零而四极矩不为零，八极矩绝缘体的四极矩和偶极矩为零，但具有量子化的八极矩。在紧束缚模型里引入正负耦合可以实现多极矩拓扑绝缘体。随后各实验小组在实验上实现了四极矩高阶拓扑绝缘体，在微波电路中实验观察到量子化的四极拓扑绝缘体[47]，声子体系中，测量机械材料的体，边和角态，发现了预言的有能隙的边界态和位于带隙内的角态[149]。

Mittal,S.等人在硅光子平台实现了量子化的四极拓扑相，揭示了零维角态的存在[150]。如图5(a)所示，纳米光子硅环形谐振腔的二维格子模型，一个元胞由4个环形谐振腔组成，每个谐振腔通过谐振腔连接（红色和绿色），耦合强度和耦合符号通过调节格点谐振环和连接谐振环的带隙大小来调节。量子化体四极矩在边上引起量子化偶极矩，在角上导致量子化的电荷。垂直移动连接谐振环引入有效跃迁相位 φ=π，原胞内合成规范通量等于π。当原胞间的耦合强度大于原胞内部的耦合强度，体系具有非平庸的偶极子极化，在带隙内支持局域的角态存在，如图5(b)所示，当耦合强度相反时，则转变为平庸的拓扑绝缘体。这些角态比零四极矩的拓扑绝缘体形成的角态更加稳定,对纳米光子系统中的一些无序免疫。零四极矩时，产生的角态易受到无序的影响，耦合到体态内，如图5(c)所示。实现四极绝缘体有多种方法，利用旋磁材料可以实现不具有偶极子极化的四极拓扑绝缘体[151]，在电介质结构中，扭转圆柱改变结构对称性实现反常四极拓扑相[152]。

6.2 二维SSH 模型

下面介绍另一种实现高阶拓扑绝缘体的方法，二维Su-Schrieffer-Heeger(SSH)[153]模型。相比四极高阶拓扑相，需要构建正负耦合，二维SSH 模型更简单。高阶二维SSH 模型角态起源于偶极子极化，它表征wannier 中心的平均位置相对原胞中心的位移[154]。非平庸的二维SSH 也可以由2D的Zak 相位表征[155]。二维光子晶体的体极化的定义如下[49]：

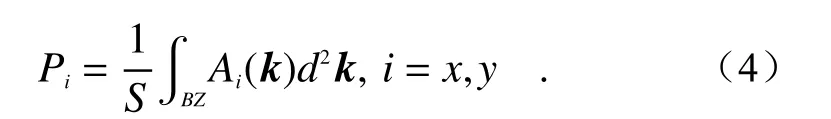
其中，S是第一布里渊区的面积，Ai(k)=i〈ψm(k)|∂ki|ψn(k)〉是贝利联络，m和n表示第m和n条带的本征态，i=x,y表示沿x,y方向。Xie等人在二维方格子结构中，模拟了局域角态和一维边界态[156]。随后两个研究组，在由电介质材料圆柱构成的四方格子中，如图5(d)[157]和图5(e)[158]所示，在微波波段利用近场扫描技术实验观测到零维拐角态。原胞内外耦合强度由介质之间的距离来控制，当原胞间的耦合强度大于原胞内的耦合强度时，处于非平庸相，极化为（1/2，1/2），反之处于平庸相，极化为（0，0）。实验测量的电场分布分别如图5(f)[157]和图5(g)[158]所示。另外，金属材料的二维SSH晶格中，金属纳米粒阵列的偶极子极化同样导致角模式[159]。同样基于SSH 晶格，Ota,Y.等人在纳米腔中实验观察到Q 值因子超过2000 的角态[160]。

人们也可以利用Kagome格子实现高阶拓扑绝缘体[49-50]。如图5(h)所示，一个Kagome格子的二阶拓扑绝缘体示意图[48]。当胞间耦合大于胞内耦合时，体极化等于（1/3，1/3），wannier 中心偏离原胞中心，处于非平庸相，边界态和角态出现在界面。文中指出，当非近邻原胞间的远场相互作用不可避免时，在光子晶体中会出现一种特殊的新型高阶拓扑相，有区别于紧束缚作用引起的高阶相。如图5(i)所示，在实验测得的态密度谱中，具有两种类型的角态，第一种由体极化引起，如图5(j)所示，而第二种就是由远场相互作用引起的，如图5(k)所示。另外，Noh,J.等人在飞秒激光直写的二维波导阵列中，在阵列的角上观察到零能模，证明了光子拓扑晶体绝缘体可以拓扑保护中间能隙的频率，并使光子缺陷模式的体积最小化，该零能模的鲁棒性由拓扑不变量保证[161]。同样，El Hassan, A.等人利用耦合波导构建的kagome格子，在可见光波段实现了局域角态[162]。

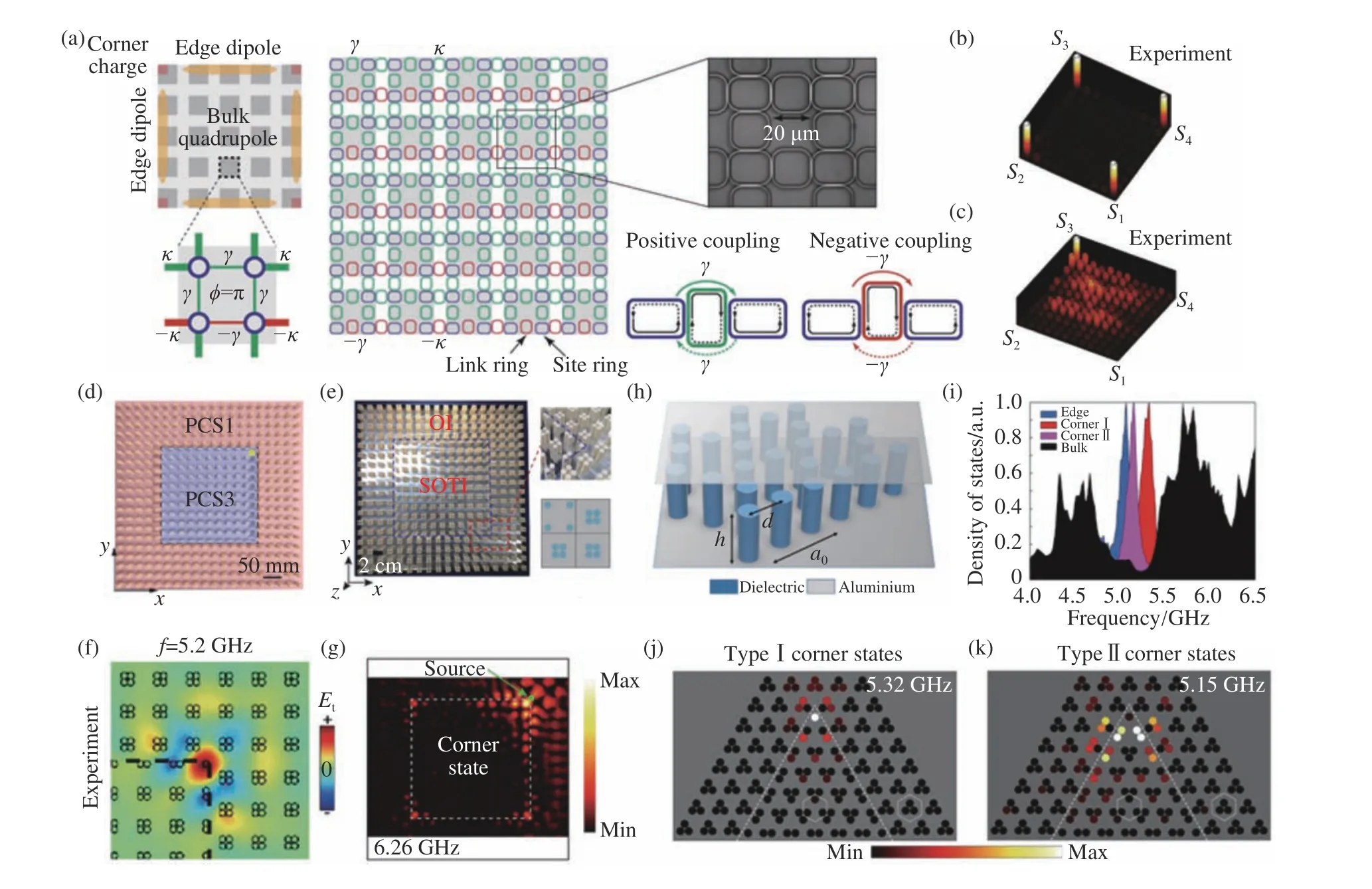
图5 (a)环形谐振腔构成的光子四极拓扑系统[150]。(b)非零四极矩时测量的空间强度分布，显示局域的角态[150]。(c)零四极矩时观测的空间强度分布，显示耦合到体态的角态[150]。(d-e)电介质材料构成的二阶拓扑系统[157-158]。(f-g)微波范围内实验测量的电场分布图，显示局域的角态[157-158]。(h)kagome格子的光子晶体结构示意图[48]。(i)实验测量的态密度谱[48]。(j-k)实验测量的场分布图[48]，分别显示类型I 的角态(j)和类型II 的角态(k)。Fig.5 (a)Schematic of the photonic quadrupole topological system composed of ring resonators[150].(b)At nonzero quantized quadrupole moment the measured spatial intensity profiles shows the localized corner modes[150].(c)At zero quantized quadrupole moment the measured spatial intensity profiles shows the corner modes coupling to the bulk modes[150].(d-e) A second-order photonic system composed of dielectric materials[157-158].(f-g)The electric field profiles measured experimentally in the microwave range showing the localized corner modes[157-158].(h)Schematic diagram of the photonic crystal structure with kagome lattice[48].(i)Experimentally measured densities of states[48].(f-g)The experimentally measured field profiles respectively show the type I corner state (j)and the type II coner state(k)[48].

高阶拓扑光子绝缘体为探索拓扑保护的局域态提供了新的研究平台。光子高阶态有诸多潜在应用，比如拓扑角态模式可以用到高Q值，低阈值的激光器上[163-164]，为发展模式体积小的激光器提供一种途径。同时宽带隙的表面波光子晶体的提出[165]，有利于集成光子学的发展。在非厄密方面，基于耦合腔在非厄密体系中可以实现区别于凝聚态体系的高阶拓扑绝缘体[166-167]。

7 总结与展望

前面基于二维系统概述了打破时间反演对称的整数量子霍尔效应、具有时间反演对称性的自旋量子霍尔效应、时间调制的Floquet 拓扑绝缘体、无序诱导的拓扑安德森绝缘体以及高阶拓扑绝缘体。拓扑光子学的发展实现了许多传统光子学所不能实现的新奇现象，也促进了凝聚态拓扑相的研究。各种拓扑相正不断涌现，光学无能隙的半金属相、非线性光学材料的非线性拓扑相、考虑增益和损耗的非厄米拓扑相、合成维度和维度映射的高维拓扑相等。

光波的拓扑保护和背散射抑制的拓扑态，对光子学有着巨大的应用潜力。拓扑态优异的传输特性将在鲁棒输运、光隔离器、激光器、量子光源、光通讯和量子计算等方面产生重要的影响。尽管拓扑光子学的应用仍有很大的挑战，比如制造工艺有限和光学材料特性的限制等，但是拓扑光子的独特性质将确保未来应用。总之，拓扑光子学在理论、实验和应用等方面都具有广阔的发展前景。