超表面透镜的像差分析和成像技术研究

刘逸天，陈琦凯，唐志远，赵 庆，片思杰，刘鑫航，林宏焘，郝 翔，刘 旭，马耀光*

（1.浙江大学现代光学仪器国家重点实验室，浙江大学光电科学与工程学院，教育部光子学国际合作联合实验室，浙江 杭州 310027；2. 浙江大学 浙江省先进微纳器件智能系统研究省重点实验室，浙江大学信息与电子工程学院，浙江 杭州 310027；3.杭州纳境科技有限公司，浙江杭州 310012）

1 引 言

光学透镜作为望远镜、显微镜、照相物镜等光学成像系统的重要组成部分，在传统光学领域得到了广泛的研究。根据费马原理[1]，电磁波从一种状态过渡到另一种状态是光程积累效应[2]导致的。为了有效调控电磁波波前，传统透镜一般通过调控界面的几何形状或折射率来实现相位分布调控，但由于天然材料的介电常数和磁导率受限，现有的传统光学透镜尺寸通常较大。随着现代光学成像系统的集成化发展，采用多功能便携式设备已经成为当前成像应用的发展趋势，大尺寸的传统光学透镜无法满足特定的应用需求。

与传统光学透镜不同，超表面透镜通过提供相位突变[3]实现对电磁波的调控，成功打破了对于光学材料厚度的依赖。超表面利用亚波长尺度单元结构的光学响应，通过限制单元结构周期可以有效消除高阶衍射，提高调控效率。另一方面，利用超表面可以设计特定的介电常数和磁导率，从而可以有效提高光学元件的设计自由度。通过具体设计超表面的几何构型和材料，可以实现透镜成像[4-6]、全息成像[7-9]、涡旋光束产生[10-11]、偏振转化[12-15]等功能，在诸多领域表现出巨大的应用潜力。

光学超表面透镜作为超表面的一种重要应用，近年来得到广泛研究，而超表面透镜的像差分析和校正对于其在成像系统中的实际应用具有重要意义。本文首先介绍了超表面实现电磁调控的几种机理，包括基于局域表面等离激元共振单元的调控和基于电介质单元的调控。然后，从光学系统像差分析的角度讨论了超表面透镜中单色像差和色像差（色差）的成因，并给出了对应的像差评价方法和像质评价指标，这对于定量评价超表面透镜的成像质量具有重要意义。本文着重整理了超表面透镜在成像方面的研究进展，包括消色差成像、消轴外像差成像、可重构成像等前沿研究领域。文章最后总结了超表面在成像方面仍待解决的问题和未来的发展方向。

2 电磁波振幅和相位调控机理

2.1 基于局域表面等离激元共振的单元结构

金属天线是一种常用的超表面构成单元，可以将传播的光集中在远小于波长的范围内，由此产生的电荷集群振荡称为表面等离激元。通过对金属天线的尺寸、形状和空间取向进行设计，可以实现在远小于波长的距离上引入相位突变。这种单元调控机理基于金属的局域表面等离激元共振（LSPR）。当入射光波的频率与金属纳米结构表面传导电子的集群振荡频率相匹配时，光在纳米结构表面将发生谐振散射产生LSPR。由于金属天线亚波长尺度具有低高宽比特点，其制造加工过程仅需要简单的剥离工艺实现[16]。

2011年，Yu 等人[3]首次用V 型天线实现了对界面相位的不连续调控，并且在中红外波段证明了广义折反射定律。V 型光学各向异性天线能够支持两种谐振特性不同的等离激元本征模式，两个谐振模式可以被入射光独立激发。通过为天线阵列选择合适的几何参数和空间取向，可以保证相邻光学天线间产生大小相同的相位差、且散射振幅保持一致。这种光学天线也可以用于新型平面成像光学元件的设计。此外，U 型天线[17]、狭缝[18-19]、纳米棒[20-22]等超表面单元结构也可用于实现基于LSPR 的等离激元超表面，大量仿真和实验[23-27]证明了等离激元超表面具有光场调控的功能。

在高频电磁波区域，金属对光的吸收较强，无法实现高效率的光场调控，而由高折射率电介质构成的超表面可以有效解决这一问题。根据单元结构的共振特性、几何形状和分析模型等，可以进一步将全电介质超表面单元分为三类：基于惠更斯原理的单元、基于截断波导原理的单元和基于贝里相位原理的单元。全电介质单元的出现大大提高了超表面光学元件的工作效率，并为解决偏振敏感性问题和色差问题提供了可能的解决方案。

2.2 基于惠更斯原理的单元结构

惠更斯原理定性指出，波阵面上的每个点都可作为次级波源形成新的波阵面。1901 年，Love[28]提出了严格意义的惠更斯原理，将次级波源定义为虚拟电流和磁流。此后，Schelkunoff 拓展了表面等效原理[29]，允许表面任意一侧存在任意场分布。2013年，Pfeiffer 等人[30]利用表面等效原理，首次在微波波段提出了惠更斯超表面，这种单元结构可以通过控制表面电极化率和磁极化率来达到消除背向散射的效果。通过调控表面极化率，结合边界条件，能够获得任意形式的散射波前。当某一表面满足：

其中 ω为角频率。根据式(2)可以发现，调整表面电磁极化率使表面阻抗和自由空间阻抗匹配时，可以获得接近1的透射率，不同的界面相位突变则可以通过控制惠更斯源的偏振特性来获得。2018年，Zhang 等人[31]设计了一种工作在5.2μm波长下的超表面透镜结构，可以实现聚焦效率约为75%的消球差聚焦，证明了惠更斯超表面单元具有以较高效率调控相位的功能。

2.3 基于截断波导原理的单元结构

利用单元结构的波导效应能够实现相位调制，单元结构引入的相移可以表示为[32]：

其 中 λd为 设 计 波 长，neff为 波 导 的 有 效 折 射 率，HWG为单元高度。通过调整单元大小和高度等几何参数，可以获得2π 相位覆盖，实现对光场的任意调控。2015年，Arbabi 等人[33]采用圆形硅纳米柱结构设计了一种偏振不敏感、大数值孔径、高效率的超表面透镜，该透镜在1550 nm 波长下的聚焦效率可达82%。该单元结构中硅纳米柱高度接近1μm，大深宽比导致加工难度较高。

相比于基于LSPR 和惠更斯原理的超表面，基于截断波导模型的超表面单元在实现高效率、大数值孔径光学器件方面具有优势；同时由于具有较高的设计自由度，在实现宽带消色差以及其它复杂光场调控方面具有一定的应用潜力。但由于受到材料限制，截断波导超表面单元往往具有较大的单元深宽比，制造加工难度较大。

2.4 基于贝里相位原理的单元结构

1956年，印度拉曼研究所Pancharatnam[34]研究得到电磁波在偏振态转化过程中会产生一个额外的相位。1984年，Berry[35]首次提出贝里相位的概念，也称几何相位。几何相位可以采用庞加莱球进行描述：在一个单位半径的球面上，其表面的每一个点都对应了一种偏振态，球体的北极代表右旋圆偏光，南极代表左旋圆偏光。当光波的偏振态从庞加莱球的北极经赤道和南极后重新返回北极，光波的相位变化为闭合路径对应立体角的一半，因此，当光线从左旋圆偏光变为右旋圆偏光时，由于相邻的纳米结构的空间方向不同，就会产生相位差，

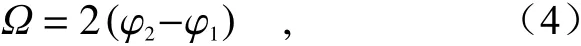
其中 φ1， φ2分别为两个相邻纳米结构的空间极化方向。

基于贝里相位的超表面设计具有非常广泛的应用价值。由于贝里相位与波长无关，故在给定某一单元结构的几何形状后，该结构的相位变化仅仅与它的方向角有关，同时相位变化的符号由入射圆偏振光的旋向决定，因此所设计单元提供的相位突变与频率无关，适用于宽带消色差等应用场景。但是贝里相位主要应用于圆偏振光，在设计的时候需要利用偏振敏感结构，相较于其他的调制方式设计自由度受到一定限制。

以上用于电磁波调控的单元结构具有超薄尺寸、较高设计自由度的优势，但相比于传统透镜，在调控效率上并不具备优势。为了获得更高效率的电磁波调控功能，研究人员通常采用光学损耗更低的全电介质单元。例如，在红外波段采用Ge[36]或Si[37-38]作为单元结构材料，在可见光波段选择TiO2[32,39-40]或GaN[41-42]等作为单元结构材料，在紫外波段用Hf O2[43]或AlN[44]作为单元结构材料。利用全电介质材料的单元结构进行超表面透镜设计，可获得接近90%的器件工作效率[32,45]，这一工作效率包括了超表面透镜的透过率和聚焦效率。

在超表面透镜的设计中，通常选取一组单元结构实现0 ～2π 的相位覆盖，用离散化的单元相位替代理想相位分布曲线。这一离散化过程会导致实际波前与理想会聚波波前有一定偏差。为了表征离散相位的影响，Aieta 等人[46]计算了不同相位梯度下超表面透镜的斯特列尔比。结果表明，当相位间隔小于π/2时，超表面透镜的聚焦效果与衍射极限聚焦之间的差别可以忽略（斯特列尔比大于0.8）。

3 超表面透镜工作性能评价

3.1 超表面透镜像差分析

在光学系统中，与光轴位置极为靠近的光线称为近轴光线，近轴光线所成的像称为高斯像。当光学系统的孔径和视场范围较小时，入射光均可看作近轴光线，这种只考虑近轴区成像性质和规律的光学称为高斯光学。当光学系统的孔径和视场范围较大时，无法满足高斯光学的要求，因此会产生像差，导致系统的分辨率和成像质量下降[47]。光学系统的几何像差包括单色像差和色差，单色像差中球差为轴上点像差，彗差、像散、像面弯曲和畸变为轴外像差。

3.1.1超表面透镜轴上点像差

对于单个球面透镜，由于透镜中心和边缘对电磁波的会聚能力不同，平行光经过不同透镜孔径时聚焦位置不同，在像面上形成弥散斑，这一成像缺陷称为球差。与传统透镜通过相位累积实现会聚效果不同，超表面透镜利用亚波长散射体的相位突变实现会聚功能。通过设计超表面透镜的相位轮廓为双曲面型分布，可以保证正入射光完美会聚在焦点位置，从而实现消球差的聚焦功能。对于波长为λ的正入射光，超表面透镜的相位分布为：

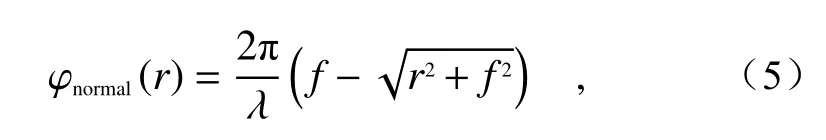
其中，f为超表面透镜焦距，r为超表面透镜单元结构的坐标位置。

虽然具有双曲面型相位分布的超表面透镜理论上不存在球差，但超表面透镜提供的附加相位是离散的而非连续分布，这种近似会导致像方波面与理想会聚波面产生偏差。在超表面透镜设计中，通常用聚焦效率来表征这种偏差，聚焦效率定义为聚焦区域光功率与透过入射光功率的比值，其中透过入射光功率定义为透过孔径光阑的光功率，该光阑与超表面透镜同尺寸且距超表面透镜出射平面约λ/2的距离[39]。聚焦区域通常定义为焦点附近的圆孔径，孔径大小一般为半高全宽（FWHM）的2～3 倍[32-33,39]或者为艾里斑大小[48]。为了和传统光学中的像质评价标准相统一，本文建议采用艾里斑大小作为聚焦区域孔径大小的定义。由此可知，图1（a）中超表面透镜的聚焦效率可表示为：

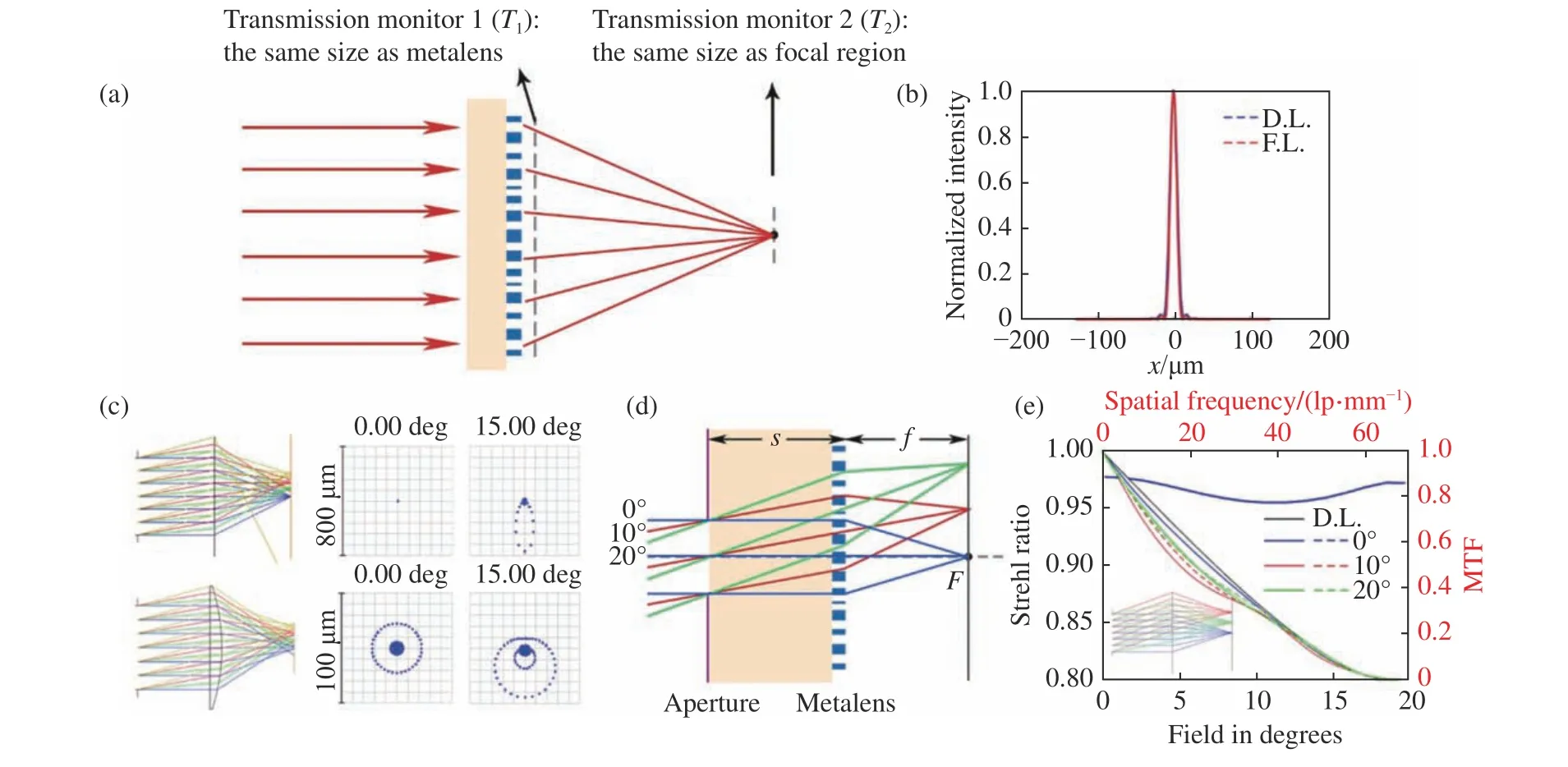
图1 超表面透镜像差分析。（a）聚焦效率计算示意图。（b）超表面透镜焦平面电场分布图，其中蓝色、红色曲线分别代表衍射极限下的焦平面电场分布和超表面会聚透镜焦平面电场分布。（c）双曲相位分布衍射平面（上）和传统球面单透镜（下）的光学系统示意图及其对应的点列图。（d）消轴外像差超表面透镜结构。（e）衍射光学元件的斯特列尔比分布及不同入射角下的调制传递函数（MTF）。Fig.1 The aberration analysis of metalens.(a)The schematic of focusing efficiency calculation.(b)The vertical cut of the focal spot of the metalens.The blue line and the red line represent the diffraction-limited intensity profile and the intensity profileof focusing metalens,respectively.(c)Theschematicsoptical system and spot diagramsof metalenswith hyperbolic phase profile(top)and traditional spherical lens(bottom).(d)The schematic of metalens designed for off-axis aberration correction.(e)The Strehl ratio and the Modulation Transfer Function(MTF)of the diffractive optical elements at different incidence angles.

3.1.2超表面透镜轴外像差

在非近轴条件下，由于轴外像差的存在，超表面透镜无法实现衍射受限聚焦的功能。对于能够实现消球差聚焦的双曲线型相位分布，可以通过计算边缘光线与主光线的光程差来表征入射角为α下的轴外像差。该光程差可以展开为多项式形式，如下[46]：

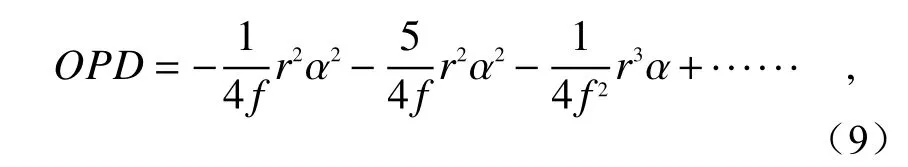
上式只保留初级像差，其中3项分别表示匹兹凡场曲、像散和彗差，无球差和畸变。彗差与孔径的平方和视场成正比，因此对于大NA 成像系统的视场范围将产生较大限制。图1（c）给出了孔径为250μm、F数为1的双曲相位分布衍射平面和传统球面单透镜在不同视场角下的点列图，可以发现双曲相位分布衍射平面光学系统在小视场下的像差较小，而在大视场下轴外像差显著增大。与之相比，传统球面单透镜虽然未能校正球差，但在不同视场角下的点列图大小基本一致，更利于实现轴外像差的校正。

考虑超表面透镜的相位轮廓与传统单薄透镜相同且孔径光阑和超表面透镜重合的情况，初级像差可以表示为如下形式[49]：

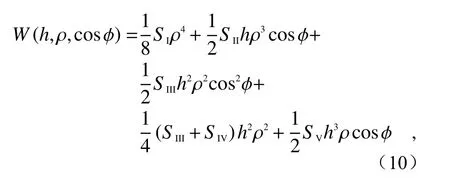
其中，h为归一化物高， ρ 和 φ表 示光瞳极坐标（ ρ为归一化径向坐标），SI～SV分别表示5种赛德和数，决定了5种单色初级像差。对于工作在单波长下的超表面透镜，考虑物位于无穷远处、光阑与超表面透镜重合，赛德和数可以表示为[49]：

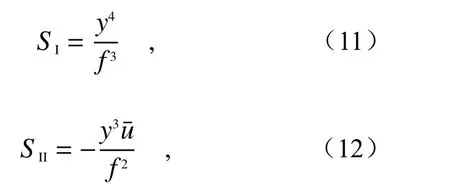
（1）由SI决定的球差与孔径的平方成正比，在保持系统相对孔径不变而整体缩放时，球差呈线性变化。

（2）彗差由SII决定，子午彗差和弧矢彗差分别为上下光线交点和前后光线交点与主光线的偏差，是由于上下（左右）光线的球差值不同产生的。

（3）超表面透镜的像散由SIII决定，表示子午光线交点与弧矢光线交点间的轴向偏差，其与超表面透镜视场的平方成正比。

（4）场曲由第三和第四赛德和数共同决定，其中SIV表示消像散时的真实像面，也称匹兹凡面。当且仅当SIII和SIV同时为零时，才能获得平的消像散的清晰像面。对于超表面和衍射透镜，其厚度相对于传统透镜可忽略不计，因此相同光焦度对应的折射率n趋近于无穷[50]，第四赛德和数为零，场曲和像散都由SIII决定。

（5）畸变是由于大视场下光学系统的成像放大率随视场变化产生的，只与主光线的光路相关。对于单个超表面透镜，在光阑与之重合的条件下，主光线通过主点沿理想方向出射，因此不产生畸变。

单色像差中，除SI、SIV仅由第一近轴光线决定外，其他赛德和数还将随光阑位置变化。当光阑移动到超表面透镜前焦面上（s=f）时，赛德和数可以表示为[49]：

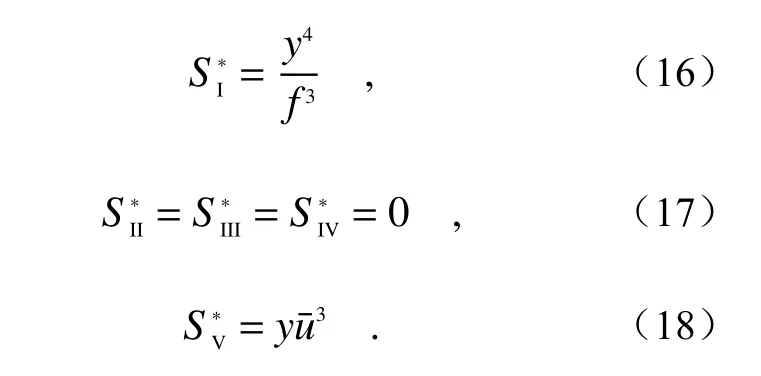
这表明超表面透镜系统轴外像差中的彗差、像散和场曲已经完全消除，系统在整个视场下的成像质量基本一致，如图1（d）所示。此类光学系统的成像质量和相对孔径大小主要受到剩余球差的限制，可以通过在光阑面增设超表面相位校正板（Corrector）进一步校正球差。

在光学系统的成像质量评价中，常用调制传递函数（MTF）和斯特列尔比（Strehl ratio）作为衡量光学系统像质的标准。光学系统有像差时，像方波面不再是球面波，这种位相差异反映为衍射图样的变化，因此衍射图样的艾里斑所占光强度的比值相较于理想成像时有所下降。二者的光强度比称为斯特列尔比，又称中心点亮度。通常认为斯特列尔比在0.8以上时，光学系统完善成像。

调制传递函数MTF是一种具有明确物理意义、又与使用性能密切相关的评价方法。在使用该评价方法时，将物体看作是不同频率谱的叠加，将物体的光强分布函数展开为傅立叶级数或傅立叶积分。因此，调制传递函数实际反映了光学系统对不同频率正弦光栅的传递能力。此外，由傅氏变换的基本定理可以证明，MTF曲线与坐标轴所围面积等于中心点亮度值，可用于评价和比较系统成像质量。由于衍射极限的存在，理想光学系统的调制传递函数随空间频率下降，调制传递函数为零时对应光学系统截止频率。

图1（e）给出了FOV=40°下某衍射光学系统的斯特列尔比分布曲线和调制传递函数曲线。该光学系统由直径为3.5 mm 的光阑和二元面（Binary 2）构成（如图1（e）插图），通过优化光阑位置和二元面系数，可以减小轴外像差。光学系统在不同视场下的斯特列尔比有波动，但始终保持在0.8以上，能够实现完善成像。但由于轴外像差仍然存在，该光学系统的MTF曲线无法达到衍射极限，尤其在大视场角下，该元件的中低频位置有所下降，这对应了光学系统对物体轮廓传递能力的下降。

在实际测量中，超表面透镜的斯特列尔比通常由焦平面中心光斑的强度积分计算得到，而MTF曲线通过焦平面光强分布的傅立叶变换获得。焦平面光强分布可以利用显微镜进行放大成像获得。将光源固定在弧形轨道上，可以对工作在大视场下的超表面透镜的性能进行表征。

3.1.3超表面透镜色差

在传统光学系统中，光学材料对不同波长的光有不同折射率，因此同一孔径不同光的光线经光学系统后与光轴交点不同，由此产生的各种光之间成像位置和大小的差异称为色差。

通常人们认为，超表面透镜的色差来源于两方面[47]：一方面需要补偿超表面透镜相位分布的频率色散；另一方面超表面透镜单元提供的相位突变也与频率有关。超表面透镜要实现消色差聚焦的功能，其提供的附加相位需要满足

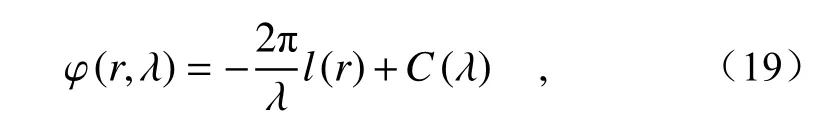
其中，l包括透镜的波前信息，C表示对不同波长的相位补偿。

在消色差超表面透镜评价方法中，比较工作带宽范围内超表面透镜聚焦位置的波动是一种比较直观的方式。此外，分别计算各波长下的聚焦效率、工作在多波长下的MTF曲线和斯特列尔比，可以更加准确地判断超表面透镜的实际聚焦效果，且便于与传统光学透镜的消色差效果进行比较。

根据消色差透镜的单元构成和色差校正原理，可将其分为利用贝里相位补偿色散和利用传播相位补偿色散两类。前者利用贝里相位与频率无关的特性，首先确定参考波长下不同位置单元的空间取向角，而后根据每个位置的色散特性匹配相应的单元结构。这一设计方法具有较高的设计自由度，常用于宽带消色差超表面元件的设计，但也通常存在对光源偏振特性的限制。后者基于波导型单元结构进行设计，由于几何参数不同的波导单元具有不同的色散特性，通过优化单元排列的方法可以实现消色差功能。该方法一般对光源偏振特性不敏感，但设计自由度较低，通常只能满足窄带宽消色差的需求。

目前为止，研究人员已经在消色差超表面透镜领域取得了许多进展，但大数值孔径、大尺寸的宽带消色差透镜设计仍是成像领域的核心挑战之一。Presutti等人[51]认为超表面无法忽略带宽限制并提供任意的群延迟，因此超表面透镜的色散特性存在一个物理边界。根据波动光学理论，器件的时间带宽积存在上限：

其中κ 为无量纲量，通常与器件的长度或折射率等特性相关。

对于背景折射率为nb、半径为R、焦距为f、数值孔径为NA 的超表面透镜，其带宽上限为：

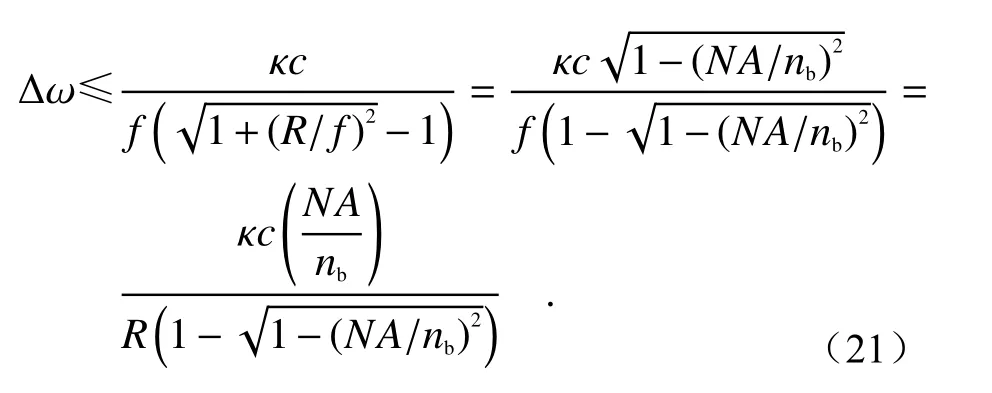
由此可知，超表面透镜的带宽、数值孔径、半径3个参数之间存在相互制约的关系。其中，超表面透镜工作频率带宽和半径成反比；在数值孔径NA 较小时，频率带宽与NA 也成反比。

目前，利用超表面单元的传播相位进行色散补偿是透射式超表面消色差中效果最好的方法。在这一消色差方法中，可将超表面单元等效为波导，其时间带宽积的上限κ 可表示为[51]：

对于这种消色差超表面透镜，其带宽上限除了受到器件数值孔径和半径的制约外，还与超表面构成单元的纳米柱高度正相关。因此，通过增加单元结构纳米柱的高度，有望实现更大带宽、大数值孔径、大尺寸的消色差成像透镜。

值得注意的是，以上带宽限制是在超表面透镜提供的附加相位满足理想消色差相位分布的条件下得到的，因此只对实现衍射受限聚焦的超表面透镜成立。对于在工作带宽范围内斯特列尔比未达到衍射极限的超表面透镜，该带宽限制有可能被超越。

3.2 超表面透镜的热分析

温度等环境因素对于光学系统的工作性能有一定影响。在传统光学系统中，这种影响主要源自几个方面：首先，光学玻璃的相对折射率受到温度的影响；其次，光学玻璃的体积会随温度变化而收缩或膨胀；此外，系统中固定装置体积的收缩或膨胀也会引起透镜间距的变化。

对于单片超表面透镜而言，温度对工作性能的影响则包括两个方面——温度变化对超表面材料折射率的影响以及温度变化对超表面单元高度、尺寸、单元间隔的影响。根据不同温度下的材料折射率和材料热膨胀系数，可以仿真得出超表面透镜在不同温度下的工作性能。

为分析比较传统光学透镜和超表面透镜受工作温度的影响程度，这里对工作在9.5μm 波长下的消球差传统透镜和超表面透镜分别进行热分析。工作在该波段的传统透镜通常由Ge材料构成，对应的超表面透镜通常以Si材料作为单元结构和衬底，两种材料在不同温度下的折射率和热膨胀系数在表1中列出。对相对孔径为1，直径为250μm 的消球差传统透镜、Si超表面透镜和Ge超表面透镜分别进行仿真，得到几种透镜在不同工作温度下的焦点位置（表1）。其中，消球差传统透镜中心厚度为10μm，Si超表面透镜和Ge超表面透镜的厚度分别为5.8μm 和4.6μm。在实际应用中，透镜尺寸通常较大（毫米量级），相应地，传统透镜的厚度也会随之增加，而超表面可以始终保持同样的厚度。当工作温度从−40℃上升到80℃时，消球差传统透镜焦距随温度的变化量约为1.596%，Si超表面透镜焦距随温度的变化量约为0.032%，Ge 超表面透镜焦距随温度的变化量约为0.121%。由此可以看出，同种材料下超表面透镜相对于传统透镜具有更好的热稳定性。此外，由于Si 具有相对较小的热膨胀系数，Si超表面透镜在热分析中表现更佳，传统透镜的焦距变化量几乎是Si超表面透镜的50 倍。

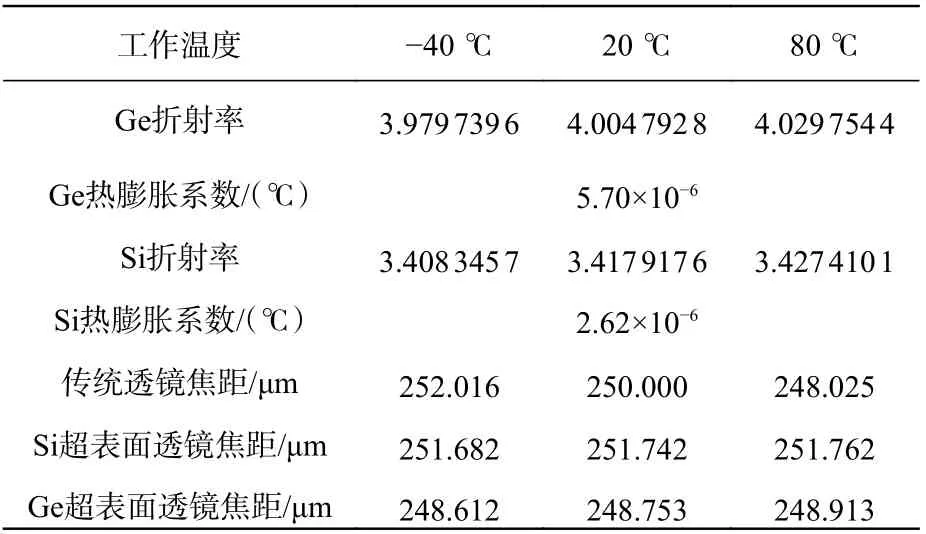
表1 传统透镜和超表面透镜热分析结果Tab.1 Thermal analysis results of conventional optical lens and metalens

4 超表面透镜成像的研究现状及应用

4.1 大数值孔径高效消球差透镜

光学系统的数值孔径（NA）是衡量系统能够接收或发射光的角度范围的重要参数，表征了系统的光收集能力和成像分辨率。大数值孔径透镜通常具有更好的成像质量、更高亮度的图像和更小的景深，目前在设计大数值孔径透镜方面已取得许多进展。

由于全电介质超表面的吸收损耗在高频电磁波区域可忽略，相对于等离激元超表面可以获得更高的透过率和工作效率。全电介质超表面由亚波长电介质天线构成，通常使用高折射率材料如TiO2[32,39-40]、GaN[41-42]、Si3N4[52]、a-Si[33,53-54]等。2016年，Khorasaninejad 等人[6]利用基于贝里相位原理的TiO2纳米天线实现了对圆偏振光的偏振转换和相位调控，该研究实现了焦距为90μm、数值孔径NA 高达0.8的会聚透镜功能。该透镜在405 nm、532 nm 和660 nm 3种波长下的聚焦效率分别可达到86%、73%和66%。实验结果表明：该超表面透镜设计能够提供可见光波段任意波长下的衍射受限聚焦，有望在光刻、光谱学、激光显微等领域得到应用。在成像系统中，除了大NA 聚焦透镜，大NA 凹透镜[20,55]在像差校正中也具有重要作用，例如凹透镜可作为级联透镜或大视场角鱼眼镜头的组成部分。2018年，Fan 等人[52]设计了一种直径为1 cm、数值孔径高达0.98、透过率超过80%的超表面凹透镜。测试结果表明：该透镜在633 nm 波长下可以将物体成像在仅为单模光纤纤芯尺寸大小的尺度范围内，有潜力应用于大视场范围的高分辨率成像。

为了获得超大数值孔径（NA>1）的超表面透镜，需要将超表面透镜浸入高折射率液体中。2017年，Chen 等人[40]首次制备了NA 高达1.1的水浸超表面透镜和油浸超表面透镜。该透镜由原子层沉积（ALD）方法制备的TiO2纳米柱阵列构成，经实验证明其可获得在532 nm 波长下的衍射极限聚焦和约为0.9的斯特列尔比。为了获得更大的NA，需要在减小超表面透镜单元周期的同时增加纳米柱高宽比，以保持电磁场被约束在TiO2内，因此NA 上限受到加工能力的限制。采用具有更高折射率的材料作为纳米柱，一定程度上放宽了这种限制，且在高折射率油浸超表面透镜设计中仍然能够保持纳米柱的光学限制能力。基于这一设计思路，Liang等人[56]选择高折射率且在可见光波段透过率相对较高的c-Si 作为纳米柱材料，他们制备的油浸透镜为迄今为止在可见光波段具有最高NA（NA=1.48）的油浸透镜。实验证明：该透镜的会聚效率为48%，聚焦光束的半高全宽FWHM 为211 nm（衍射极限FWHM 为182 nm）。这种基于c-Si的超表面透镜有潜力应用在浸入式应用和大数值孔径光学系统中，对于超分辨显微镜、消色差透镜、光学捕获和水下成像有重要意义。

4.2 消轴外像差超表面透镜

在传统光学透镜中，轴向照明下可以实现无像差聚焦，而在离轴照明下会产生离轴像差。基于这种现象，2013年，Aieta 等人[46]提出了一种由弯曲基板和超表面单元构成的超表面透镜，其能够实现无球差和彗差的聚焦。相对于平面超表面透镜，这一弯曲的超表面透镜在倾斜照明下表现出良好的聚焦效果和更接近衍射极限的MTF（图2（a））。但是，在球面基板上加工超表面单元具有较大的难度。

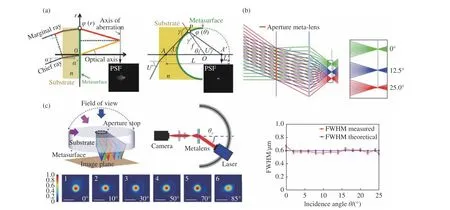
图2 消轴外像差超表面透镜设计。（a）平面超表面透镜（左）和弯曲基板超表面透镜（右）示意图及二者在中心波长1.55μm、入射角10°条件下的点列图（PSF）[46]。（b）级联透镜校正剩余球差原理示意图（上）及不同角度入射光下级联透镜聚焦光斑的FWHM 测量值（下）[58]。（c）超大视场角单层平面超表面透镜示意图（左上）、用于测量不同入射角下聚焦光斑的实验装置示意图（右上）和不同角度入射光下的聚焦光斑测量结果（下）[59]。Fig.2 Metalens designs for monochromatic aberration correction.(a)Schematics and Point Spread Function(PSF)of a flat lens(left)and an aplanatic metasurface(right)illuminated with parallel monochromatic light at λ=1.55μm and incident at an angle α=10°[46].[Reprinted/Adapted]with permission from[ref.46]©The Optical Society.(b)The operation of the metalens doublet in terms of the correction of spherical aberration(top)and measured FWHM of focal spot intensity profiles at different incident angle θ (bottom)[58].Reprinted (adapted)with permission from (GROEVER B,CHEN W T,CAPASSO F.Meta-Lens Doublet in the Visible Region[J]. Nano Letters,2017,17(8):4902-4907.).Copyright (2017)American Chemical Society.(c)Schematic of a single-layer planar metalenswith an ultra-wide FOV(topleft),schematic of experimental setup for imaging a focal spot produced by metasurfaceat variousincident angles(topright)and measured focusing spots at all incident angles(bottom)[59].Reprinted (adapted)with permission from(SHALAGINOV M Y,AN S,YANG F,et al..Single-Element Diffraction-Limited Fisheye Metalens[J]. Nano Letters,2020,20(10):7429-7437.).Copyright (2020) American Chemical Society.

另一种消轴外像差的超表面透镜是以Chevalier Landscape镜头为参考设计的级联透镜[49]，这种传统镜头具有较小的孔径光阑，孔径光阑将正入射和斜入射的光线分离，使其由镜片的不同位置聚焦。通过设计镜片的曲率和孔径光阑位置可以一定程度上消除彗差等轴外像差。对于平面衍射光学元件，三阶彗差和像散可以分别表示为[49]：

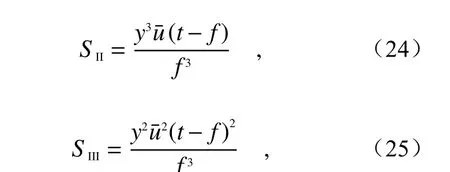
其中u为物方孔径角，y为边缘光线在透镜上的高度，t为孔径光阑与透镜距离。可以看出，当t=f即孔径光阑放置在透镜前焦面位置时，可以有效消除彗差和像散，而衍射透镜的场曲始终为零。将这种设计方法推广到超表面透镜领域，可以消除所有轴外像差。2016年，Arabi 等人[57]设计的大视场超表面级联透镜工作在850 nm，具有仅为0.9的F数和超过60°的视场范围，聚焦效率可达到70%。在可见光波段，2017年，Groever 等人[58]设计了一种工作在532 nm 的级联透镜，消像差原理由图2（b）给出，级联透镜的相位分布分别根据施密特相位板和球面镜进行设计，其数值孔径为0.44，视场范围达到50°。级联透镜能够表现出接近衍射极限的成像质量，有潜力应用于显微、摄影、计算机视觉等领域的光学系统中。

在超广角全景成像和投影的应用中，需要具有更大视场范围的超表面透镜。2020年，Shalaginov 等人[59]设计了一种视场范围超过170°的单层中红外全景超表面透镜，超表面透镜包括单层超表面和集成在基底上的孔径光阑，不同角度入射光经过孔径光阑后经基底折射和超表面聚焦后会聚在焦平面上（如图2（c））。该超表面由CaF2衬底和PbTe纳米颗粒构成，由于材料在中红外波段具有低光损耗和高折射率的特点，并且能够同时支持电偶极子和磁偶极子谐振，从而能同时实现2π 相位覆盖和较为统一的透过率分布。经图2（c）所示的实验装置验证，设计得到的全景超表面透镜在入射角从0°增大到85°的过程中，会聚效率从45%变化到32%，角度敏感性相对较低。实验表明，不同视场角下聚焦光斑大小基本一致，不同视场下的斯特列尔比均在0.8以上，满足衍射受限聚焦的要求。

为了实现良好的消像差效果，消轴外像差超表面透镜的相位分布与非球面镜类似，通常定义为径向坐标ρ 的偶次多项式的形式：

其中R为超表面透镜半径，an为相位分布系数，用于优化得到目标视场下的最小聚焦尺寸，具体an可以通过光学设计软件中的光线追迹功能优化获得。

消轴外像差超表面透镜的设计通常采用时域有限差分方法（FDTD）和衍射积分（The Kirchhoff Diffraction Integral）算法相结合。首先在亚波长尺度上进行FDTD全波仿真，获得构建超表面透镜模型所需光学响应对应的单元结构；而后在宏观超表面透镜系统中，采用衍射积分计算方法对整个超表面透镜的聚焦特性进行高效验证和优化。2019年，Chu 等人[60]对广义惠更斯-菲涅尔原理（GHF）、广义瑞利-索默费尔德衍射理论（GRS）、惠更斯原理（HP）这几种衍射积分计算方法进行了物理原理的介绍和准确性比较，证明了GRS在包括倏逝场和非近轴区域的空间场分布计算中具有更高精度和更广泛的适用性。与全波仿真相比，该方法在显著提高计算效率的同时能够保持足够的准确性，对于未来基于超表面器件的设计和优化具有潜在影响，例如亚波长近场成像、全息和单光子检测等需要准确高效的非近轴近场计算的重要应用。

4.3 消色差超表面透镜

工作带宽是光学器件的重要特性，具有消色差功能的超表面透镜有潜力应用于显微物镜、光谱仪等光学成像系统中。在基于超表面的光学系统中，可以通过调控不同波长下的谐振获得色差校正。根据消色差超表面透镜的工作带宽，可将其分为分立波长消色差、窄带消色差和宽带消色差3种。

4.3.1分立波长消色差超表面透镜

2015年，哈佛大学Aieta 等人[61]首先利用空分复用原理，提出了在1300、1550和1800 nm 3个分立波长下实现消色差功能的超表面光学元件。其中，超表面透镜由非周期排列的耦合矩形电介质谐振腔构成，透镜分为3个区域，分别针对3个波长实现聚焦效果。由于空分复用方法一定程度上牺牲了透过率和分辨率，该消色差透镜的会聚效率在3个分立波长下分别仅为9.8%、10.3%和12.6%，平均会聚效率较低。

2018年，Zhou 等人[62]提出了另一种多层结构超表面透镜，用于实现分立波长消色差。如图3（a）所示，与单片超表面透镜不同，两片相互分离的超表面透镜可以提供叠加的相位和透过率，增加了设计自由度，从而能够筛选出同时符合1180 nm 和1680 nm 两个分立波长下相位曲线和透过率条件的纳米柱参数组合。实验结果表明：利用该结构设计得到的NA=0.42的超表面透镜对1180 nm 和1680 nm 波长的聚焦效率分别为38%和52%。该设计方法可以通过继续增加超表面透镜层数实现多个分立波长下的消色差聚焦。

图3 消色差超表面透镜设计。（a）将两个不同波长的光聚焦在同一位置的超表面级联透镜示意图。每层超表面的相位共同提供了两个不同波长下所需的双曲线相位分布[62]。（b）反射式消色差超表面透镜示意图（左）以及工作波长500 nm和550 nm 下反射光附加相位与纳米柱宽度的关系（右）[64]。（c）两种集成谐振单元的偏振转换效率（红色）和相位分布（蓝色）图[42]。（d）不同色散特性超表面透镜所需的相对群延迟和相对群延迟色散分布。（e）由超表面校正透镜和传统球面镜构成的光学系统示意图[67]。（f）分区消色差超表面透镜示意图[69]。Fig.3 Metalensdesigns for chromatic aberration correction.(a)Schematic diagram of a metasurface cascade lens that focuses two different wavelengths of light at the same position.The phases at each layer together to provide the required hyperbolic phase profiles at the two different wavelengths[62].Reprinted(adapted) with permission from(ZHOU Y,KRAVCHENKO I I,WANG H,et al..Multilayer Noninteracting Dielectric Metasurfaces for Multiwavelength Metaoptics[J]. Nano Letters,2018,18(12):7529-7537.).Copyright(2018)American Chemical Society.(b)Schematic of an achromatic metalens working in reflection mode(left).Computed reflection phase shift as a function of the nanopillar width at two different wavelength of 500 and 550 nm(right)[64].Reprinted(adapted) with permission from(KHORASANINEJAD M,SHIZ,ZHU A Y,et al..Achromatic Metalens over 60 nm Bandwidth in the Visible and Metalens with Reverse Chromatic Dispersion[J].Nano Letters,2017,17(3):1819-1824.).Copyright(2017)American Chemical Society.(c)Polarization conversion efficiency(red curves)and phase profile(blue curves)for integrated-resonant unit elements(IRUEs)[42].Reprinted(adapted)with permission from(WANG S,WU P C,SU V-C,et al..A broadband achromatic metalens in the visible[J]. Nature Nanotechnology,2018,13(3):227-232.).Copyright (2017)Shuming Wang et al.(d)Required relative group delays (left)and relative group delay dispersion (right)as a function of metalens coordinate.(e)Schematic of a hybrid lensconsisting of a metacorrector and a spherical lens[67].Reprinted (adapted) with permission from (CHEN W T, ZHU A Y,SISLER J,et al..Broadband Achromatic Metasurface-Refractive Optics[J]. Nano Letters,2018,18(12):7801-7808.).Copyright (2018)American Chemical Society.(f)Schematic drawing of a multizone RGB-achromatic metalens showing achromatic focusing of RGB light coming from different lens locations[69].From[LIZ,LIN P,HUANG Y-W,et al..Meta-optics achieves RGB-achromatic focusing for virtual reality[J]. Science Advances,2021,7(5):eabe4458.].Reprinted with permission from AAAS.

4.3.2窄带消色差超表面透镜

分立波长消色差超表面透镜只能在几个目标波长下实现无色差工作，并不是真正的消色差光学元件。针对此问题，2017年加州理工学院的Arbabi等人[63]提出了一种工作在连续窄带光谱下的消色差透镜，他们在不提高结构复杂度的情况下设计了一组相位覆盖包含多个2π、具有不同色散的矩形a-Si单元结构，通过优化算法选取同时满足目标相位条件和色散最小条件的单元结构作为透镜组成部分。根据这种设计方法，他们在1450 nm 到1590 nm 的连续窄带宽内实现了消色差透镜功能，透镜直径为500μm，焦距为850μm。同年，Khorasaninejad 等人[64]基于类似方法设计了可见光窄带消色差超表面透镜，工作波长范围为490 nm～550 nm。这种超表面透镜由图3（b）所示的反射式方柱TiO2波导单元构成，通过调整单元参数可获得较大相位覆盖范围。该项工作还对相位分布公式进行了改进，引入了一个波长相关的参考相位C，相位分布为：

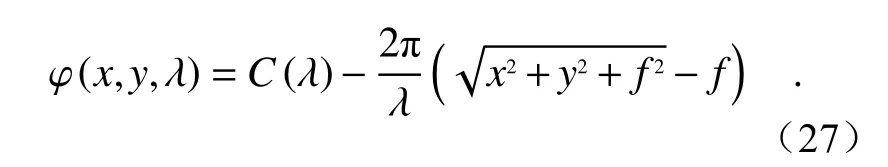
由公式(27)可知，不同波长下的目标相位分布可以相差一个常数项，且不会对聚焦效果造成影响，引入了新的设计自由度，故可以通过粒子群算法优化获得一组符合所有波长下相位要求的单元结构。优化得到的超表面透镜有效数值孔径为0.2，直径为200 μm，焦距为485μm，在工作波段的聚焦位置误差仅为2.7μm，消色差效果较好。这种窄带宽消色差方法具有结构简单、易加工、消色差效果好的优势。通过应用折射率更高的材料构成单元结构，可以进一步提高设计自由度和拓展工作带宽范围。

4.3.3宽带消色差超表面透镜

由于窄带的连续波段消色差的实现仍然难以满足全色检测和成像等实际应用的要求，宽带消色差方法被提出。2017年，Wang 等人[65]提出了一种设计方法，成功实现了1200 nm～1680 nm 的连续宽带范围内的消色差聚焦，聚焦效率约为12%。他们将透镜的相位分布分为波长相关和波长无关两部分：

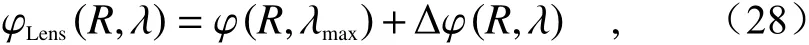
其中，第一项为波长无关的基本相位曲线，可以通过单元结构的贝里相位调制获得；第二项与1 /λ呈线性关系，表示不同入射波长之间的相位差，可以利用耦合金属纳米柱（MNRs）的集成谐振产生，如图3（c）所示。通过贝里相位和集成谐振单元相位补偿相结合，该反射式等离激元超表面可以提供准确的消色差相位轮廓，实现消色差聚焦。由于透射式光学元件在可见光波段具有广泛应用，2018年，Wang 等人[42]将该设计方法推广到可见光波段，利用GaN 纳米柱结构及其反结构作为集成谐振单元，这种单元的强谐振特性为相对较大的相位色散补偿提供了可能。他们据此设计了一种工作在400 nm～660 nm 的NA 为0.106的消色差透镜，平均透过率达到40%，相比于等离激元超表面透镜在效率上有较大提升。但这种基于贝里相位的设计方法，必然受到入射光为圆偏振光的条件限制，具有一定的局限性。

2018年，Chen 等人[48]提出了另一种消色差理论，将相位轮廓进行泰勒展开，得到：

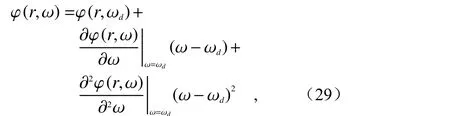
其中，ω,ωd和r分别为角频率、设计角频率和径向坐标。两个高阶项分别定义为群延迟和群延迟色散，群延迟项补偿了波包在焦点位置到达时间的差异，而群延迟色散项保证了波包形状的一致性，二者共同实现宽带色散调控功能。基于以上方法，进而提出了一种NA 为0.2的偏振不敏感的可见光波段消色差超表面透镜[66]。该透镜对于各种线偏振和圆偏振入射光聚焦效率保持一致。这种色散调控方法理论上可以用于设计具有任意色散特性的光学元件，如图3（d）所示。

在可见光波段实现的宽带消色差超表面透镜存在透镜尺寸受限的问题，一般在100μm 量级以下。对于大尺寸超表面透镜而言，由于需要获得较大的群延迟范围，对单元结构高度的要求超出了目前的加工技术限制。采用超表面校正透镜和传统球面镜结合的方式（图3（e））可以缩小需要的群延迟范围，在合理的单元结构高度下实现大尺寸透镜组的宽带消色差功能。Chen 等人[67]证明了该超表面校正器可以使单个球面透镜在几乎整个可见光范围内实现消色差功能，并且可以极大地扩展NA=1.45油浸物镜的工作带宽，使其工作在紫外到近红外波段。这种大尺寸超表面校正透镜与传统光学元件结合，在降低设计复杂度和器件体积的同时进一步提高了光学系统的成像质量。

宽带消色差功能一般由复杂结构构成的单层超表面透镜实现，这类消色差透镜往往面临加工难度大、设计自由度低的问题。因此，研究人员提出了基于多层超表面透镜的消色差理论。2020 年，Li等人[68]引入了传统光学中有效阿贝常数的概念，利用分别具有正负光焦度的超表面透镜组合实现了可见光波段宽带消色差的功能。文章仿真验证了一种由圆柱单元构成的总焦距ft=36μm、直径D=19.5μm 的超表面透镜组合系统，实现了可见光波段聚焦位置差小于2 μm、平均聚焦效率达到50%的消色差聚焦。该设计方法具有结构简单、设计自由度高的优势，有望推动多功能平面光学元件的进一步实现。

由于超表面单元提供的群延迟范围有限，可见光宽带消色差超表面透镜的尺寸通常限制在几十微米以内。2021年，Li等人[69]提出了一种根据单元结构群延迟覆盖范围对透镜进行分区的方法（图3（f）），实现了对超表面透镜色散和相位的分别调控，并且设计了一种直径为2 mm 的超表面透镜，打破了群延迟对透镜尺寸的限制。该器件的NA=0.7，能够在470 nm～670 nm 波段内实现斯特列尔比接近1的衍射极限聚焦。

在对超表面透镜的消色差效果进行评价时，相比于不同波长下聚焦位置的偏移量，偏移量与焦距的比值更能准确反映超表面透镜的消色差性能。在衡量传统光学透镜的消色差效果时，像面位置上物点的像为一个彩色弥散斑[70]，通过透镜的色球差曲线、多波长点列图以及宽带MTF曲线对色差产生的弥散斑进行表征，这对于消色差超表面透镜性能的评价具有借鉴意义。

4.4 其他特殊功能超表面透镜

除了实现传统透镜的功能，超表面透镜还可以对图像实现旋向可控的放大和缩小，即这一超表面透镜集成了对于右旋入射光的会聚功能和对于左旋入射光的发散功能。2012年，Chen 等人[20]基于贝里相位原理、利用亚波长偶极子天线阵列设计了一种超表面透镜，通过调整单个天线的空间取向角 φ，可以获得φ=±2φ的局部相位突变。该超表面透镜对于左旋圆偏振光入射和右旋圆偏振光入射具有完全相反的贝里相位，从而实现对右旋光会聚而对左旋光发散的功能。这一双极性等离激元超表面透镜在旋向转换过程中的耦合效率仅为5%，对于实际应用而言还很低，但该超表面透镜的设计方法有利于进一步促进偏振敏感聚焦等前沿研究和应用。

此外，超表面可用于设计锥透镜，这种特殊透镜可以作为涡旋光束发生器[71-72]或者高斯-贝塞尔光束转换器[73-75]使用，在眼科手术、光学诱捕、显微镜和望远镜领域有较多应用。当轴锥透镜角度为β时，入射光获得的锥形相位延迟为[2]：

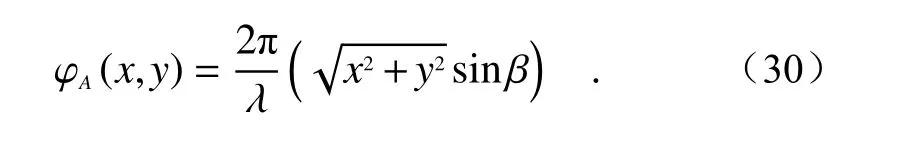
2012年，Aieta 等人[4]计了8种V 型等离激元天线，对圆偏振光产生相对恒定的振幅和梯度变化的相位，并且设计得到半径为0.45 mm、锥角为0.5°的锥超表面透镜。研究人员使用电子束刻蚀（EBL）在硅晶圆上制备了金纳米天线图案。同样，利用贝里相位实现波前调控的锥超表面透镜可将圆偏振高斯光束转换为贝塞尔光束[76]。通过对超表面提供的附加相位分布进行调整，可以进一步获得高阶贝塞尔光束[76]或者实现螺旋锥透镜[74]的功能。

超表面锥透镜有助于突破光学设备的成像限制，2017年，Gao等人[73]提出了一种由超表面透镜和锥透镜构成的成像系统，锥透镜是由矩形纳米孔阵列构成的金属超表面，相较于同样尺寸和数值孔径的超表面透镜，该系统可以分辨更小的距离，为高分辨率成像提供了更多可能。该系统目前工作在近红外波段，设计加工可见光超表面锥透镜可以进一步拓展其应用场景。

目前大多数的超表面透镜设计可用于替代传统光学元件，与管镜、偏振片等元件结合，应用于复杂光学系统中。因此，此类成像光学系统整体仍然具有较大体积，无法发挥超表面透镜超轻超薄的核心优势[77]。近年来，为了充分利用超表面集成度高的特点，研究人员将超表面透镜应用在医疗内窥、集成成像等领域。2018年，Pahlevaninezhad 等人[78]成功将超表面透镜应用于内窥系统中。相对于传统的基于球透镜或格林透镜的内窥系统，超表面透镜解决了像散造成的图像畸变问题，并且实现了对焦深和横向分辨率的提高。这一研究有利于进一步推动内窥光学成像在临床方面的应用。2020年，Zhou 等人[79]将超表面透镜和微分器集成，设计了一种工作在透射模式下的集成化图像处理系统，实现了对图像的高分辨率（4μm）传输和边缘检测。这一集成化器件有望应用于生物成像、计算机视觉等领域，也为超表面光学器件实现较为复杂的光学调控提供了思路。同年，Xu 等人[80]将硅单元超表面透镜直接固定在CMOS传感器上，设计了一种高度集成化的大视场显微成像器件。该器件利用超表面透镜阵列进行偏振复用，从而打破了视场角和分辨率之间的制约关系，为超表面透镜实现集成大视场成像提供了解决方案。

利用超表面透镜阵列，2019年Lin 等人[81]实现了全色光场相机的功能，其中透镜阵列由60×60个直径为21.65μm 的消色差超表面透镜构成，白光下分辨率为1.95μm。这一光场相机可以对场景中不同深度的物体进行重构，从而有潜力应用于机器视觉、虚拟现实、增强现实等各个领域。

4.5 可调及可重构超表面透镜

多数超表面和超表面透镜仅具有唯一固定的功能特性，但在实际应用中，可调超表面透镜和可重构超表面透镜能够方便实现多种功能并节约成本，应用于扫描显微镜或扫描相机。可调超表面的光学响应可以受到力、热、电磁场等外界物理量的主动调控。相变材料处于不同状态时，其光学和电学性质存在巨大差异，适合实现这一特殊功能。

Ge2Sb2Te5（GST）为一种相变材料，其结晶温度约为160℃，而糊化温度约为600℃[82]。利用GST在晶态、非晶态下的折射率不同，可以实现对出射场振幅和相位的动态调控[83-85]。此外，通过控制结晶比例获得部分晶态GST，可以增加调谐范围和分辨率。利用相变GST层和金纳米棒结构，2016年Chu 等人[86]设计了一种双焦点等离激元柱透镜，该透镜在非晶态和晶态下的焦距分别为0.5 mm 和1 mm。VO2是另一种常用的相变材料，在加热时会发生从绝缘体到金属的可逆变化，其复折射率也在宽光谱范围内随相变发生变化。根据这一性质，Kim 等人[87]于2019年首次实现了对VO2反射的近红外电磁波的主动连续的相位调控，通过焦耳热对VO2有效介电常数进行主动控制可以获得可调谐相位响应。与GST相变材料相比，Ge2Sb2Se2Te1（GSST）在晶态和非晶态下都在红外波段具有更好的宽带透明特性，可以有效减小光学损耗。2021年，Shalaginov等人[88]设计了一种由GSST 惠更斯单元构成的变焦超表面透镜，该器件工作在5.2μm 波长下，晶态和非晶态下的聚焦效率分别为21.6%和23.7%，并且有效解决了不同深度物体间的串扰问题，极大提高了变焦超表面透镜的性能。2018年，Yu 等人[89]利用金属镁的氢化和脱氢反应可逆地调节超表面中的有效像素，设计了一种双焦点柱面超表面透镜。对于633 nm 的右旋圆偏振入射光，氢化前后超表面透镜的焦点分别处于z=200μm 和z=100μm 处，如图4（a）所示。这种动态转换超表面也可用于实现光束转向、全息加密等功能。

改变超表面几何结构的可拉伸超表面透镜是另一种用于实现连续变焦的常用方法[90-93]。2016年，Ee 等人[91]基于贝里相位原理设计了一种由柔性PDMS衬底和金纳米棒构成的超表面（如图4（b））。在拉伸衬底的过程中，单元晶格常数的变化导致透射光波前相位分布发生改变，由此引起的焦距调制可以表示为f′=s2f，其中s表示超表面拉伸比，f和f′分别为拉伸前后的焦距。这种机械拉伸调节方法具有加工简单高效的优势，但由于其理想相位分布与单元位置的关系是非线性的，在拉伸过程中实际相位分布与理想值的差距会导致像差的产生。图4（b）给出了超表面透镜焦点位置和焦点处场分布与拉伸比的关系，在大拉伸比条件下，聚焦光斑电场分布展宽明显。

Arabi 等人[93]设计的基于微机电系统（MEMS）的可调级联超表面透镜在灵敏度和调节范围上有较大优势。该级联超表面透镜由两片靠近的大光焦度凸透镜和凹透镜构成，其中一片位置固定而另一片可移动，如图4（c）所示。通过施加电压的方式调整两片超表面透镜间距，可以实现对超表面透镜组合焦点的调节。该设备灵敏度较高，微调（～1μm）其中一片超表面透镜可以获得约60屈光度的大范围调节，总体调节范围可以达到300屈光度以上。该电控级联超表面透镜可用于对不同位置物体进行成像，实验装置和成像结果如图4（d）所示。将这些不同焦距的透镜阵列集成在同一芯片上，可以实现几kHz 频率的深度扫描，有望应用于紧凑型快速扫描内窥镜和光纤探针共聚焦显微镜等设备中。

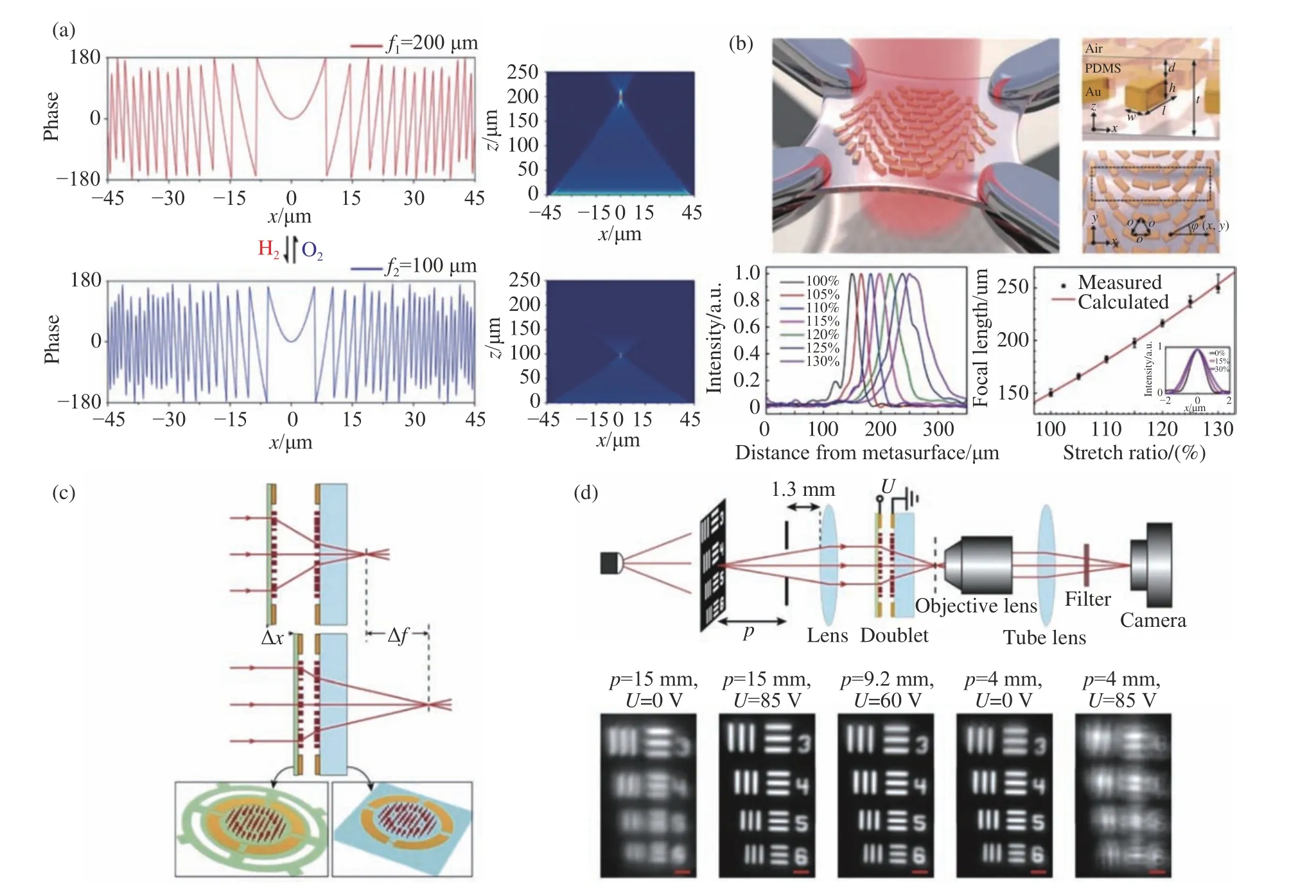
图4 可调及可重构超表面透镜设计。（a）氢化反应前后超表面透镜的相位分布以及对应的电场强度分布[89]。（b）可拉伸PDMS衬底超表面示意图（上），纳米棒的长、宽、高以及埋入深度分别为l=240 nm,w=100 nm, h=70 nm, and d=200 nm。不同拉伸比s对应的透射圆偏振光沿光轴的强度分布（左下）以及焦距测量值和计算值（右下）[91]。（c）可调级联超表面透镜示意图。该超表面透镜由一片固定透镜和一片可移动透镜构成[93]。（d）超表面级联透镜成像装置示意图（上）及不同外加电压和成像距离p对应的成像效果（下）[93]Fig.4 Tunable metalens and reconfigurable metalens.(a)The calculated phase discontinuity profiles and the corresponding full-field intensities of the metalens before and after hydrogenation,respectively[89].Reprinted(adapted)with permission from (YU P,LIJ,ZHANG S,et al..Dynamic Janus Metasurfaces in the Visible Spectral Region[J]. Nano Letters,2018,18(7):4584-4589.).Copyright(2018) American Chemical Society.(b)Schematic illustrations of a metasurface on stretched PDMS(top).Length,width, height and embedded depth of each nanorod is l=240 nm,w=100 nm,h=70 nm,and d=200 nm,respectively.Intensity distributions of transmitted cross-polarized light with different s along the optical axis(left-bottom).Measured(black dots)and calculated(red line)focal length of the lens as a function of s(rightbottom).The error bars represent ranges where intensity is larger than 90%of peak intensity.Inset shows transverse intensity profiles of the focused beam with different s[91].Reprinted(adapted) with permission from(EE H-S,AGARWAL R.Tunable Metasurfaceand Flat Optical Zoom Lenson a Stretchable Substrate[J]. Nano Letters,2016,16(4):2818-2823.).Copyright(2016) American Chemical Society.(c)Schematic illustration of the proposed tunable lens,comprised of a stationary lens on a substrate,and a moving lens on a membrane[93].Reprinted(adapted) with permission from(ARBABIE, ARBABIA,KAMALISM,et al..MEMS-tunable dielectric metasurface lens[J].Nature Communications,2018,9(1):812.).Copyright(2018)Ehsan Arbabi et al.(d)Schematic illustration of the imaging setup using a regular glass lens and the tunable doublet (top).Imaging results(bottom),showing the tuning of the imaging distance of thedoublet and glass lens combination with applied voltage[93].Reprinted(adapted)with permission from(ARBABI E,ARBABI A,KAMALI S M,et al..MEMS-tunable dielectric metasurface lens[J].Nature Communications,2018,9(1):812.).Copyright (2018)Ehsan Arbabi et al

2019年，Chen 等人[94]提出了一种利用超表面透镜色散进行高分辨率层析成像的方法，并设计了基于GaN 消球差超表面透镜的层析成像系统。其中，GaN 超表面透镜基于贝里相位进行设计，具有较大数值孔径（NA=0.78），横向和纵向分辨率可分别达到775 nm 和6.7μm。相比于利用复杂机械构件进行扫描的传统层析成像方法，利用色散进行波长调焦的方法更加稳定和高效。而超表面透镜具有体积小、易集成、色散大的特点，同时克服了衍射透镜低效率、低信噪比等缺陷，在高度集成化的层析成像应用方面具有很好的实用价值。

2020年，Lininger 等人[95]将液晶与超表面透镜相结合，通过在超表面结构中注入具有不同折射率和双折射特性的液晶，实现了对于超表面透镜聚焦位置和聚焦光斑的调控。这种调控方法本质上是通过改变超表面单元的背景折射率实现的，具有实现动态可重构超表面透镜的潜能。

5 结 论

本综述从超表面设计原理出发，对超表面透镜的像差及其工作性能进行了理论分析，对当前超表面成像领域存在的技术问题进行了相关探讨，最后总结了超表面成像透镜近年来的研究进展和具体应用。

由于传统光学元件的大体积难以满足光学领域集成化的需求，作为平面光学元件的超表面和衍射光学元件越来越多地应用于成像和聚焦等领域。

衍射透镜获得附加相位的原理与传统透镜相似，通过光在介质中传播获得的光程引入相位变化。多级衍射透镜为实现高效率的平面透镜提供了一种方法，并且具有消除像差的潜力。与衍射透镜的相位变化引入机制不同，超表面透镜通过纳米结构单元的光学响应引入相位变化。由于亚波长结构具有波导模式、米氏散射模式、近场模式等多种谐振模式，超表面可以提供自由度很高的光场调控功能[96]。此外，超表面透镜的亚波长尺寸使其在集成光学和光子学领域具有广泛应用前景[97]。

在大数值孔径成像方面，超表面透镜已经表现出超越衍射透镜的性能[98]，研究人员已经证明了多个数值孔径大于0.9的高效超表面透镜[6,33,54]，但具有这一功能的衍射透镜尚未在实验中实现。在消色差方面，衍射透镜通常利用多级衍射消色差，这一方法不可避免地增加了衍射透镜的刻蚀深度；而超表面透镜的几种消色差方法通常会受到工作效率或工作带宽的影响。考虑到超表面透镜的消色差方法通常具有更高的结构自由度，未来在多色成像领域仍有望表现出超越衍射透镜的性能。并且，超表面透镜独特的偏振特性使其能够实现特殊形式的光调控，从而应用于偏振成像、高效偏振器和偏振敏感光学等领域。尽管目前的超表面透镜已经能够实现多种光调控功能，要实现工作在大视场下的无像差、大数值孔径、高效率成像还需解决以下几类问题：

首先，在消单色像差超表面透镜中，超表面透镜视场范围的增加通常都伴随着剩余球差校正难度的增加。目前的解决方案需要利用孔径光阑和级联透镜进行像差校正，这就导致加工中的对准环节精度要求较高，增加了工艺上的难度。此外，大视场超表面透镜的数值孔径通常较小，在设计过程中需要在二者之间进行权衡。

在消色差超表面透镜中，消色差方法不具有可缩放性，即当透镜尺寸增加时，满足消色差条件的难度也随之增加，因此大尺寸的宽带消色差超表面透镜难以实现。并且，消色差超表面透镜往往聚焦效率较低，高效率的消色差方案还需要进一步的研究。

最后，可调超表面透镜的调控速度对于基于超表面透镜的扫描和成像设备也十分重要。目前可调超表面透镜主要基于温度进行调节或通过机械拉伸进行调节，还无法满足对于调控速度的需求。此外，要利用超表面透镜平台实现对于波前的完全动态调控还存在一定挑战。解决这一问题对于未来多功能超表面透镜和集成可重构超表面透镜的实现具有重要意义。