人工原子间耦合：超构表面调控电磁波的新自由度

林 婧，李 琦，邱 孟，何 琼，周 磊

（复旦大学 物理学系 表面物理国家重点实验室，上海 200438）

1 引 言

电磁超构材料（Metamaterials，MTMs）是指由亚波长人工微结构单元(“人工原子”)按一定宏观序组成的人工复合材料[1], 它的诞生突破了自然材料的限制，展现出了奇异的光学响应及对电磁（光）波丰富的调控自由度，近年来引起了人们广泛的研究兴趣。相较于自然材料，超构材料的优势在于人们可任意设计“人工原子”和体系的宏观“序”，在亚波长尺度下实现对电磁波的局域调控，进而实现诸如负折射率、超成像、电磁隐身[2-4]等自然材料无法实现的奇异物理现象。然而，虽然超构材料在调控电磁波方面取得了卓越的成就，其结构复杂、尺寸庞大、损耗相对较高（特别是在光波段）等缺点也是不容忽视的，这使得各大研究组都把目光转向了更易加工的二维超构材料——电磁超构表面（简称“超构表面”）。相较于三维材料，超构表面易控制损耗，体积小，重量轻，在集成光学、通讯、军事等方向，均有非常大的应用前景。近年来，人们在利用超构表面实现光场调控方面取得了重大突破，发现了许多奇异物理现象和新规律（如拓展 Snell 定理、高效全息成像、光子自旋霍尔效应[5-7]等）和具有优异光学性能的功能性器件（无色散超宽带波片、超透镜、高效表面波耦合器[8-10]等）。超构表面也正因其对光场的超强调控能力而成为近年来物理学、信息学以及相关交叉学科的研究热点。

“人工原子”是超构材料最核心的结构，其通常是具备很强电磁响应能力的光学共振结构。在不同情形下，人们需要设计出具备各种功能的电磁共振体，以满足超材料对“人工原子”的需求。然而，随着科学和社会的发展，人们的需求逐步扩大到包括大带宽或多频应用、非线性现象和密集集成等领域，单个人工原子的设计自由度有限，性质也比较单一，无法提供充足的自由度来实现各种各样的设计需求。近年来，由多类材料/结构成分构成的复合人工原子因为相互间的耦合作用可提供更大的调控自由度和更具辨识度的物理现象而备受人们关注。在先驱性的实验工作中，人们发现了非常多的有趣的人工原子耦合所导致的物理现象。如Stefan Maier 课题组在 2003 年在金属局域共振体（LSPR）之间通过近场耦合传递能量，从而实现了等离子波导[11-12]，使得集成光学的集成度打破了波长限制。Giessen 课题利用单根金属棒跟两根金属棒的耦合效应实现了电磁感应透 明（Electromagnetically Induced Transparency，EIT）现象[13]。此后，人们利用各种各样的耦合共振体实现了多种奇特的光学响应[14-18]。在这些研究中，耦合行为对光学响应的调控能力主要表现在共振频率、共振Q值、偏振响应等方面。

从上述回顾中可以发现，耦合的相关研究具有重要的科学意义和应用价值。相比人们在实验方面取得的长足进步，对于耦合问题的理论理解却远未令人满意。人们研究耦合体系时，基于计算电磁学的数值模拟工具能够输出可信的结果，然而这种方法不仅费时费力，而且无法揭示现象背后隐藏的物理机制，往往难以提供物理上的洞见；已有的经验理论（如耦合模理论[19-20]、Fano 公式[21-22]等）则往往由于依赖于唯象参数的拟合而更适用于对已有结果的分析。因此，亟需建立一套既能精确描述耦合作用，又可以明确提炼重要物理过程的理论，进而帮助科研人员深入理解与耦合相关的物理图像，以大量节省工程仿真设计中的前期试错成本。

本综述将围绕处理人工原子间耦合问题的理论工具展开讨论。在回顾前人的一些处理方法之后，重点介绍本课题组近期发展的一系列理论方法，从光子封闭体系的少体问题到周期体系，再到开放体系下的复杂光子共振结构，系统介绍了各种体系下对于耦合问题的理论理解，以及如何利用这些理论工具实现角度色散调控、谱线线型调制等具有特定电磁波调控功能的新型超构表面。最后，基于以上相关研究进展，展望了这些新理论/新技术对超构表面未来研究及应用产生的重要启发和影响。

2 超构表面人工原子及其耦合行为的研究

2.1 常用的人工原子结构及其光学响应探究

超构材料对于光的调控主要源自于人工原子被激励产生共振时的响应。接下来以4 种常用于人工原子设计的极具代表性的纳米共振结构为例，来探讨这些结构的基本响应特性。这4 种基本结构分别是细长的金属纳米棒、金属-绝缘体-金属(MIM)结构、金属开口环结构(SRR)和介质纳米盘，它们是构建光学和近红外光子共振体系(如超材料和超表面等)必不可少的组成部分[23]，如图1 所示。

如图1(a)所示，最常用的人工原子设计之一就是具有电偶极共振的细长金属纳米棒结构。纳米棒结构的电响应往往呈现很强的各向异性，仅能被电偏振方向沿着长轴的外场激励。在微波波段，电磁波激励下的天线产生的来回震荡的感应电流使共振总是发生在半波长的整数倍处[24]，而等离激元模式则将其延伸出了金属棒几何结构以外，这是高频段纳米棒共振模式同射频段偶极天线的一个显著不同(图1(b))。图1(b)～1(c) 展示了体系的散射谱线与吸收谱线及被激励的电偶极矩与入射场波长的关系。可以看到，电偶极矩的振幅在共振处达到最强，并且共振处两侧的相位经历接近π 的变化，这是非常典型的电偶极响应特征[25]。中间被纳米尺度电介质隔开的两个金属纳米棒组成的结构被称为MIM 结构，如图1(d)所示。基于杂化理论[15]，可以将MIM结构的共振模式理解为由上下两个(相同)纳米棒之间的相互作用而形成的两个新的杂化模式，其中对称模式对应两纳米金棒中响应电流同向，能量较高，对外整体表现出较大的总电偶极矩。而反对称模式中两纳米棒的响应电流始终方向相反，能量较低，相反的电流使得结构对外的总电偶极矩被压制，形成的等效电流环路使结构表现出磁响应(见图1(e)～1(f))。图1(g)所示的金属开口环结构(SRR)在几乎任何频率范围内都可实现磁响应。由于随着SRR 的缩小，真实金属的响应由感应电流主导变为位移电流主导，这导致磁共振波长不再随其尺寸缩小而减小，因此在光频，人们往往使用MIM共振来获得磁响应。图1(h) 为其散射谱线及吸收谱线，从图1(i)可以看出，尽管SRR 通常被称为磁性共振结构，其实它可被偏振方向沿着x轴的正入射光同时激励起沿y轴方向的磁偶极矩以及沿x方向的电偶极矩, 并可通过改变纳米结构弯曲形成的开口大小来控制这两个偶极矩之间的相对强度。最后一种常用的共振纳米结构是硅纳米盘(图1(j))，它是近红外全介质惠更斯超表面的重要组成部分[26]。米氏理论指出球形粒子通常同时具有电共振和磁共振[27]，其中磁模仅在磁电[28]或高介电常数[29]结构中才能被激发。米氏理论的总体结论通常适用于任意形状的纳米颗粒，因此可以认为纳米盘和立方体结构也具有电和磁的共振特征(见图1(k)、1(l))。在可见光波段，硅的吸收开始增加，因此人们往往使用二氧化钛(TiO2)替代硅来设计介质超表面，该材料在整个可见光谱中具有相对较高的折射率(n>2.3)，并且其材料吸收可以忽略不计[30]。

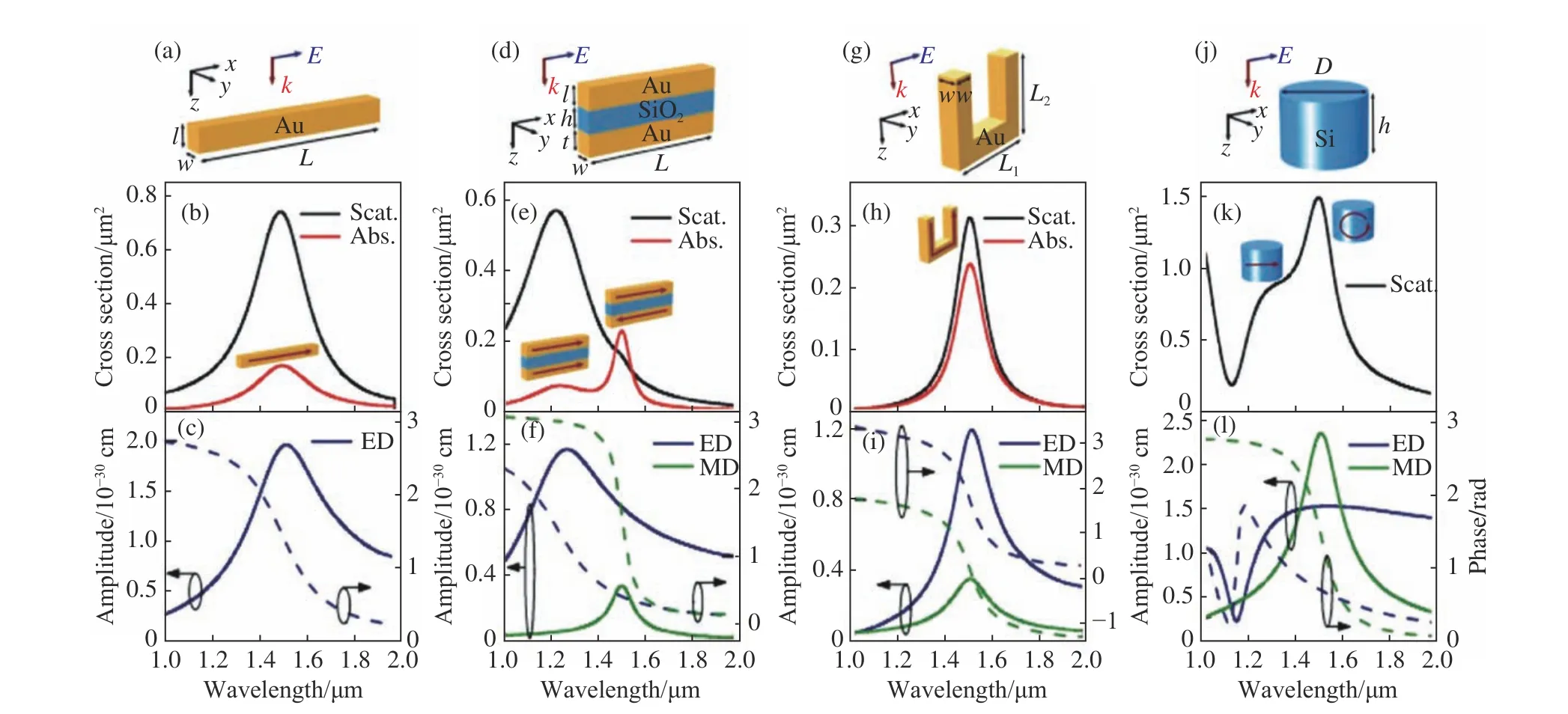
图 1 常见人工原子结构及其光学响应[23]Fig. 1 Typical Meta-atoms structures and their optical response[23]

单一人工原子自身具有的光调控效果已经足够满足一些简单的需求，然而，单个模式一旦确定下来，其性质也基本确定下来，功能单一，难以进行调控以满足各种复杂的实际需要。比如一些具有很强辐射能力的结构，可以起到传输信息的作用，而一些具有非常高Q响应的结构，则可以用于增强局域光场，然而，单一结构人工原子往往只能有单一用途，当同时需要很强的场增强和传输信息的能力时，单一结构就无能为力了。

由此，耦合的重要性便凸显出来。在纳米结构中，局域电磁模式之间的耦合对上述结构电磁特性调制起着关键作用。比如，Liu 等人通过堆叠多层SRR 结构构建了一种三维磁性超材料，当SRR 发生相对旋转时，层间相互耦合将使体系模式特性变得相当有趣[31]。再比如，由于金属结构具有不可避免的能量损耗，人们进行了许多关于全介质共振体的研究，通过非对称的介质二聚体耦合实现了光束转向、大角度偏转、反对称透射等有趣现象[32-35]（图2）。所有这些实验表明，耦合对确定这些复杂系统的电磁特性至关重要，突破了单一人工结构的限制，成为调制电磁波的新自由度。

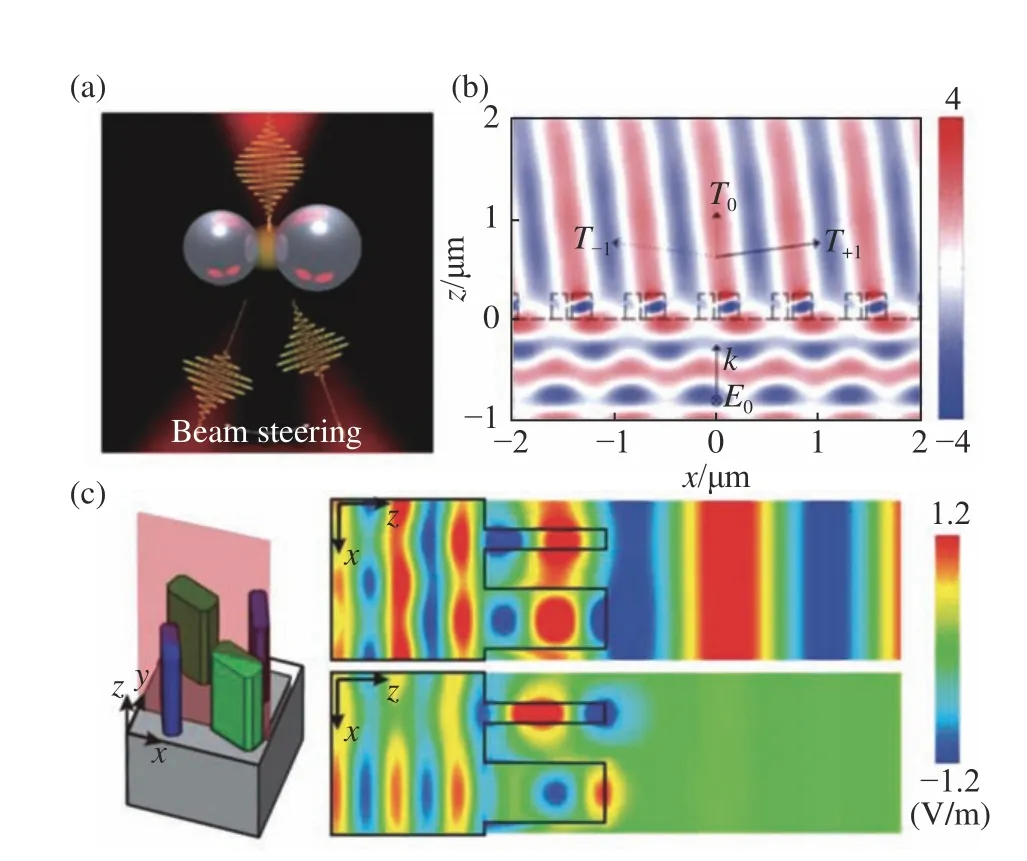
图 2 非对称介质光子共振体耦合结构[32-35]Fig. 2 Asymmetric dielectric resonators[32-35]

2.2 耦合现象的常用理论方法

对于耦合现象的研究，在实验方面取得很多成 果的同时，理论研究也有一定的进展。主要的理论研究方法可分为数值方法和参数化理论模型两大类，常用理论方法结果见图3。

数值方法包括有限单元法(Finite Element Method, FEM)、时域有限差分法(Finite-Difference Time-Domain, FDTD)和 离 散 偶 极 近 似法(Discrete Dipole Approximation, DDA)等。数值方法应用极为广泛，几乎所有体系都可以利用其进行一定的分析，特别是对于不能够解析求解麦克斯韦方程组(或拉普拉斯方程组) 的体系。以DDA 为例，其主要处理方式是将人们感兴趣的研究对象划分为N个可被极化的元素所构成的立方晶格[36]，对于处理形状不规则且周围环境较复杂的纳米颗粒特别有效(图3(a)[37])。

除了数值方法之外，人们还建立了很多理论模型(例如，LC 等效电路模型、Fano 模型、耦合模理论等）以直观解释基础的物理图像。

LC 振荡电路模型将阻抗表示为几种基本类型的简单模块的组合(电阻、电容、电感等)，把体系模型化（见图3(b)），将求解空间等效成三维电路，电磁波的传播便可被电路中等效电流/电压的传输所替代。由此人们将阻抗的概念从电流拓展到场和波，可基于位移电流J˜d=−iωD˜来定义光阻抗，在足够高的频率下，位移电流相比于传导电流J˜=σE˜ ( σ表示电导率)占据主导地位。参照电阻抗定义，对于亚波长尺寸的均质粒子，光阻抗可定义为通过纳米粒子的局部电势差与位移电流的通量的比值。如果粒子是亚波长的，那么从表达式可以看出所定义的光阻抗是粒子的固有特性，与周围环境无关，基尔霍夫电路定律可以像适用于常规电子电路一样适用于该体系[38-39]。在该阻抗定义下，根据介电常数的正负，等效光电压和位移电流的震荡之间保持±90°的相位差，可类比LC 震荡电路得到光学共振结构的等效电容/电感。每个纳米粒子都具有自己的固有光学阻抗，可将不同的纳米粒子组装起来形成更复杂的模块化等效电路，并且可以通过常规电路理论轻松设计其响应[40]。早在超材料发展的初期，Pendry 就利用 LC 振荡电路模型研究了耦合的双开口环结构, 南京大学的刘辉课题组也用此模型对复杂SSR 结构做出了非常有效的解释[16]。

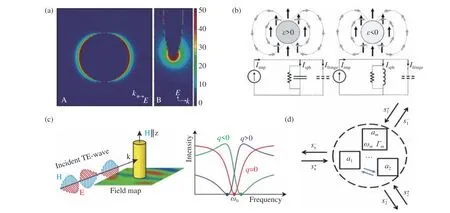
图 3 常用理论研究方法。(a)离散偶极近似法[37]；(b) LC 等效电路模型[39]; (c) Fano 理论[41]；(d) 耦合模理论Fig. 3 Theoretical methods. (a) Discrete dipole approximation[37]; (b) LC equivalent circuit model[39]; (c) Fano theory[41];(d) coupled mode theory

当离散的量子态与连续态发生干涉时，会发生Fano 共振，并且在吸收光谱 δ(E)中表现出来，其线型由著名的Fano 公式描述：

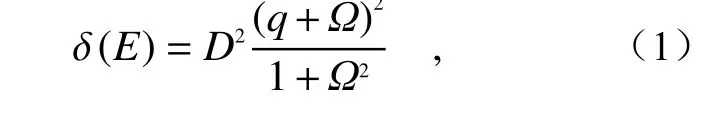
其中E是能量，q=cotδ是 Fano 参数， δ是连续谱的相移， Ω=2(E−E0)/Γ ，其中 Γ和E0分别是共振宽度和能量，D2=4sin2δ。公式(1)被证明可适用于多种系统的不同光谱(包括透射和散射)。近年来，随着光子体系研究的发展，Fano 共振引起了很多关注。实际上，几乎任何共振状态都可以被视为具有复频率的准离散状态，从而可以用Fano共振来描述。光学体系中的Fano 共振是由两个阻尼率差异很大的振子耦合而产生的，所得的光谱(图3(c))显示出典型的不对称性，在波峰和波谷之间急剧变化。光学体系的研究主要集中于Fano 共振产生的陡峭的透射-反射曲线，以及从透射到反射的急剧转变。这个特性可用于实现光子体系中的一些开关器件[41-42]。

耦合模理论是描述开放体系下多个模式和多个端口相互作用的建模工具[19,43](图3(d))，其基本方程如下：

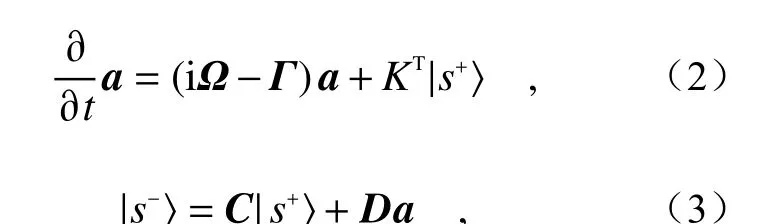
其中，a=(a1a2···an)T表示每个共振模式的振幅， |s+〉与 |s−〉分别描述体系入射和出射波函数， Ω与 Γ均 为n×n的厄米矩阵，分别用于描述每个模式的共振频率与辐射损耗，KT代表每个端口的入射波函数与模式的相互作用，D代表被激励的共振模式与出射波函数在端口处的耦合，C矩阵描述的是背景矩阵，即共振模式不存在时背景对入射波函数的散射。式(2)和式(3)分别描述了体系模式在入射波激励下的响应与体系的散射过程。时间反演与能量守恒条件保证了这些参数之间并不是完全独立的，满足：

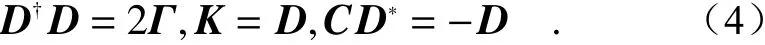
其中，“†”与“∗”分别表示取共轭转置与取共轭，后文同理。由此便可通过拟合来分析多个共振模式耦合的复杂情况，该理论在研究光学共振体系时有着广泛的应用和影响。耦合模理论给出了清晰的物理图像，在帮助人们理解的基础上可以进一步指导真实体系设计。

从以上分析可以看出，上述理论方法或依赖数值模拟获取参数，无法提供清晰的物理理解，或运用唯象理论从已有结果出发推测物理图像，依赖于从实验或者全波模拟中拟合得到的参数，往往用于分析已有的结果，而并不能起到直接预测未知结果的作用。这些方法由于缺乏对体系物理本质的深入探究，对于耦合问题的理解仍远远不够。

针对这一问题，本研究团队展开了一系列研究。从麦克斯韦方程组出发，推导出不依赖于拟合参数即可有效描述电磁共振体耦合之间的理论方法，并给出相应的物理理解，然后，利用该方法解释实际遇到的耦合体系问题。通过深入理解人工原子间的耦合方式，以探寻超构表面设计新机理。

3 近似封闭体系的耦合理论

3.1 光子紧束缚近似理论与等效模型理论

当两个光子共振体相互靠近时会耦合产生新的、杂化的共振，这是一个基本现象，在物理学的所有领域都可以观察到。所谓的紧束缚方法(TBM)或原子轨道的线性组合（LCAO）理论就是通过计算局域波函数的交叠积分来计算耦合[44]。紧束缚理论可以帮助人们理解耦合并且在理论指导下调制耦合强度，或者计算能带结构。

TBM 最初用于研究固体中的电子性质，是量子体系中处理耦合问题的非常有效的方法之一。薛定谔方程的波动性质意味着在量子体系下发展起来的数学方法在电磁学中也适用[45]。早期光子体系的TBM 要么基本上是经验公式，交叠积分（即耦合强度）通过拟合全波计算或实验数据获得[46-47]，要么往往只能直接计算介电常数 ε和磁导率 µ与频率无关的非色散系统的波函数交叠积分[48-49]。这是一个严重的限制，因为大多数构成等离子体系和光学超构材料的结构不可避免地具有频率依赖（色散）的介电常数。因此，建立一个统一的理论来研究一般光子体系（无论是否色散）中的耦合问题是非常必要的。

Raman 和Fan 将麦克斯韦方程组写为“类薛定谔方程”的形式，建立起适用于色散体系的哈密顿形式[50]。考虑光子晶体、超构材料等纳米周期性光子结构，假设构成体系的色散介质的介电常数满足洛伦兹形式如下：

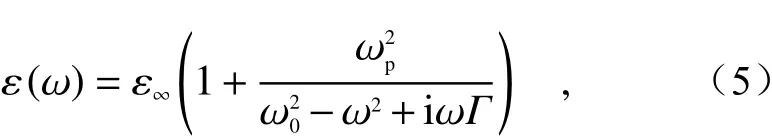
其中 ωp为等离子频率， ω0为特征频率， Γ为吸收阻尼。这个介电常数的色散形式可以由金属中电子对外界电场的响应推导而来。设电场为E˜，磁场为H˜ ，引进极化场P˜与极化速度（即极化电流）v˜=dP˜/dt作为辅助场，就可以得到色散介质中电磁场的基本方程为：

考虑无损耗体系，即Γ=0的情况。定义内积为：

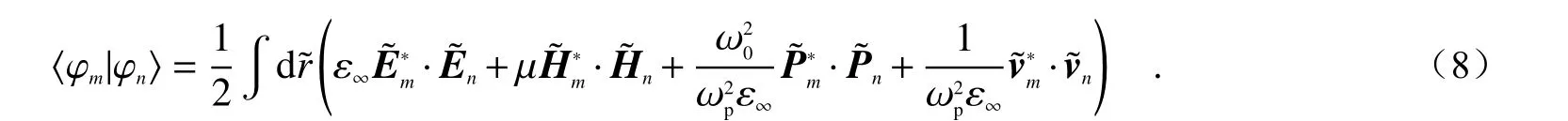
对于本征频率不同的本征函数满足正交关系〈φm|φn〉=δmn，值得注意的是〈φm|φm〉的物理意义为模式m的能量，这里默认已经做了归一化处理。

由此色散光子晶体和光学超构材料的能带结构的求解问题便转化为一个标准的矩阵本征值问题。通过数值求解该本征值即可获得体系的能带与本征模式的波函数场分布（见图4）。

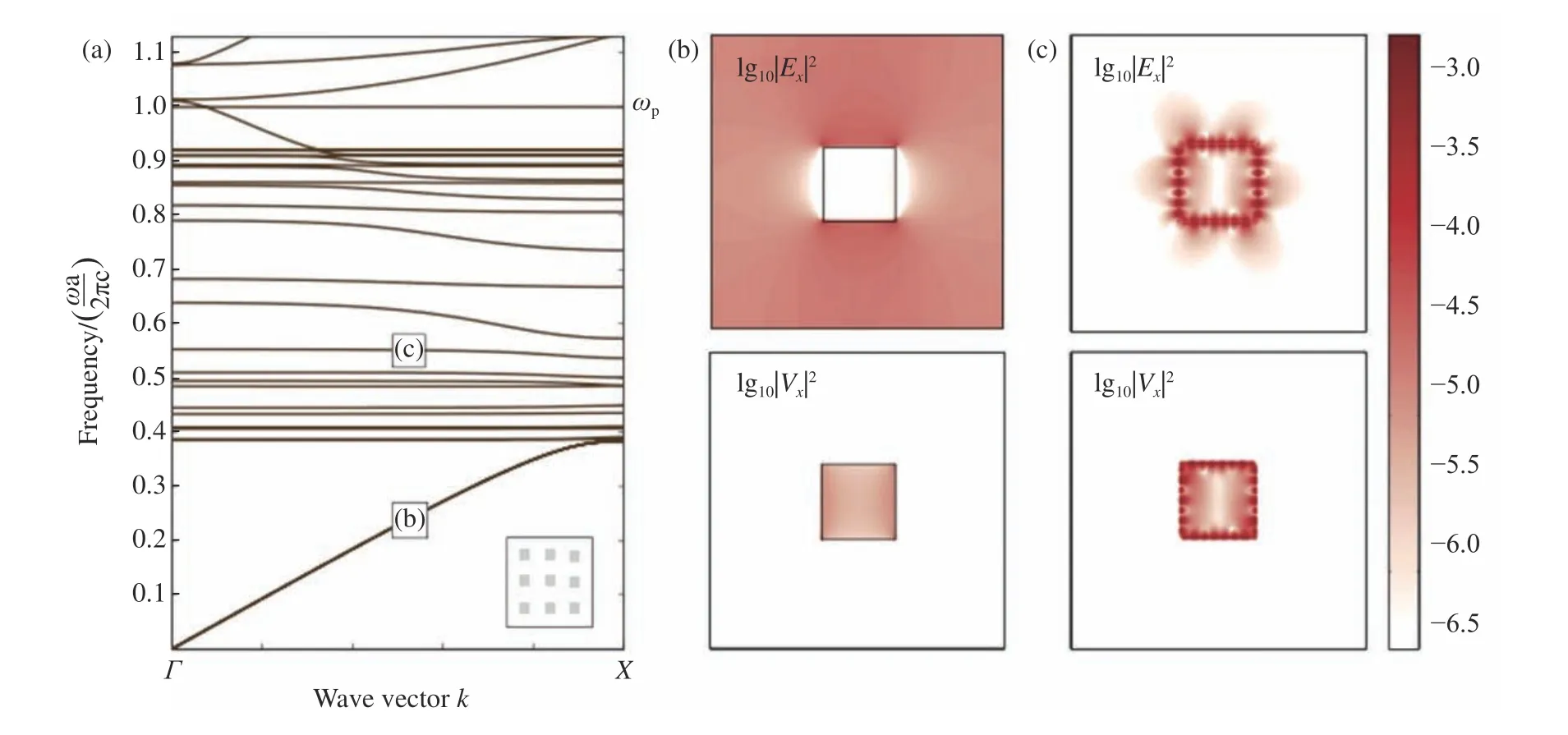
图4 (a)光子晶体能带与(b-c)本征波函数场分布[50]Fig.4 (a)Computed band structure and (b-c)visualizationsof two field components[50]

由此便获得了可以完全描述电磁共振/散射体系的类薛定谔方程，并且定义了其度规和内积的形式。有了这个形式，就可以借用量子力学中各种成熟理论方法来计算光学共振体系的耦合。考虑高Q近似下，每个共振体共振时波函数高度局域在结构周围，由此可将体系近似为封闭体系，将共振结构自身近似为与时间无关的微扰“势场”。此近似下，便可将电子体系的紧束缚方法代入色散光子共振体系的紧束缚近似理论推导中，由此求解在此微扰下体系的能级与波函数所发生的变化[51]。

考虑在背景(介电常数和磁导率分别为εh(ω)和 µh(r˜))中有多个全同的光子散射体(第i个共振体介电常数和磁导率分别为 εi(ω,r˜)和 µi(r˜))的体系，假设介电常数都满足洛伦兹模型（公式(5)）。首先考虑只有单个散射体的情况，此时体系可被描述为：

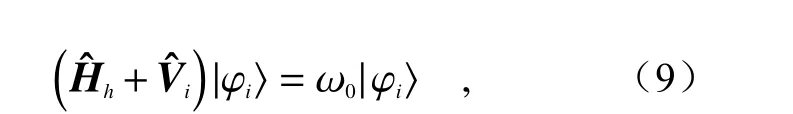
其中Hˆh为 背景体系的哈密顿量，Vˆi为该共振体提供的势场：

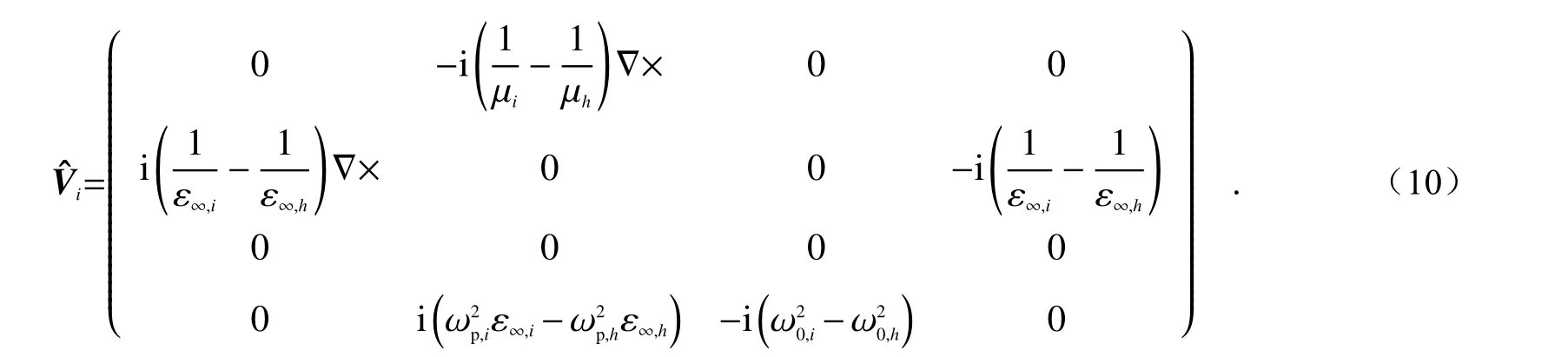
由此可解得该共振体的一系列本征模式的波函数分布与对应的本征频率。

接下来考虑有多个共振体的体系，其哈密顿量为：

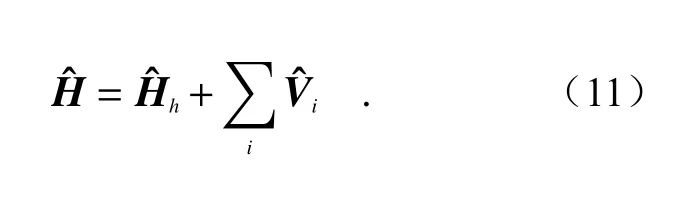
其中〈Φ|Φ〉是归一化因子，代表局域模式的电磁总能量。这里值得注意的是，由于所处理的体系并不是真正的封闭体系，因此计算归一化因子时不能直接对全空间进行能量积分，这是因为远场辐射的存在会导致能量积分发散。故需要减除辐射能的影响，从而获得模式的局域场部分能量。可以通过积分计算出以单一共振体为球心，不同半径R的球体空间内部的能量E，然后画出能量E与半径R之间的关系图，如图5(a)(右图)所示，最终得到的E-R曲线切线在纵轴上的截距就是想要的减除了辐射能量的局域场能量，即归一化因子〈Φ|Φ〉。 最后，通过对角化哈密顿量Hi,j=(f0+ti,i)δi,j+ti,j(1−δi,j)即可得到整个耦合体系的本征频率与本征波函数分布。

从最简单的两体耦合系统开始进行理论验证。如图5(b)所示，使用能在508.2 THz达到共振的单金属棒，另加一根全同的金属棒之后，发现原始的共振频率会劈裂成两个。为了从多个方面验证理论计算的精确性，改变两根金棒的距离和它们各自的形状，分别计算其耦合作用，并进行模拟和理论的对比。可以看到，模拟结果与紧束缚方法的预测结果完全吻合。

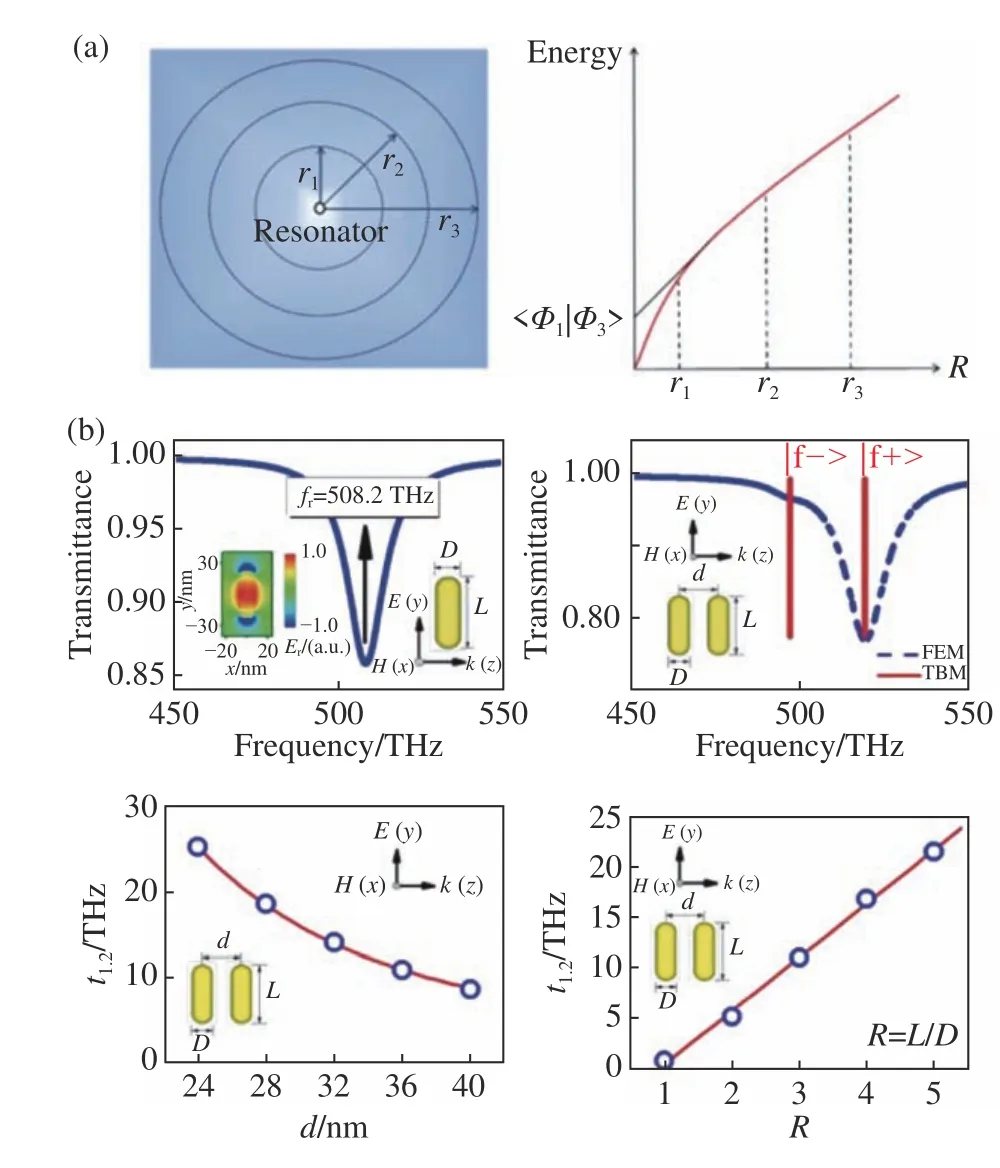
图5 (a)归一化方法；(b)光子紧束缚理论的数值验证[51]Fig.5 (a) Normalization method;(b)numerical verification of generalized TBM[51]

紧束缚方法可以预测很多常用光学共振结构的耦合结果，其对于各种形状、各种摆放方式的共振体，都可以非常精确地计算出共振频率的偏移与劈裂。然而，紧束缚方法作为形式理论，仍缺少足够清晰的物理图像来理解耦合现象，可以更进一步地将其模型化。

对于两体耦合体系(图6(a))，从t1,2的原始表达式(式(12))出发导出一个简单且物理图像清晰的解析形式。将波函数形式代入式(12)，由内积定义(式(8))计算可得：

现在对式(13)所描述的方程做进一步展开。先将电场展开为标势和矢势的贡献E˜2=−∇φ2−(−iω0)A˜2，代入式(13)可得：

其中：

从表达式中可以看出，p˜,m˜和 〈Φ|Φ〉是仅有的需要基于单共振体进行数值计算的3个参数。一旦从第一性原理计算中获得这3个参数，一般情况下的耦合就可以很容易地由式(17)～式(18)中推导出来，无需进行进一步的数值计算。这个重要特征不仅节省了大量的数值计算工作，而且使物理图像对于非专家和实验人员来说更加清晰。由此便成功地（从第一性原理）导出了一个可描述一般形状的光子共振体之间耦合行为的解析模型[52]。

解析模型包含了共振结构等效电偶极子和磁偶极子之间的所有相互作用项，其有效性通过各种结构的全波模拟得到了很好的验证。有了等效模型，可以不用通过复杂计算就可以预测复杂结构中等离子体耦合的丰富行为，并且可以理解复杂现象背后的内在物理。例如，我们发现在所设计的模型中，电磁交叉相互作用项可以导致某些耦合系统中出现有趣的模式反转行为（见图6(b)）。此外，可根据有效模型得出一个简单推论：通过简单地改变共振结构的相对角度，耦合强度可以从正值持续调整到负值，从而产生许多有趣的应用。如图6(c)所示，当体系的耦合强度非常低的时候，色散关系趋向于一条平的直线，能量传输发生在非常深亚波长区域内，这使得能带体系中传输波的群速度非常低，为实现简单深亚波长结构中的慢波传输提供了一种新颖的机制，与采用布拉格散射[54]或电磁感应透明效应[55]的慢波实现机制非常不同。

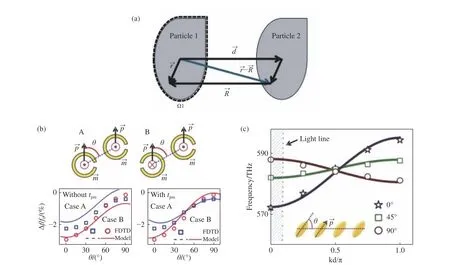
图6 (a)两体耦合示意图；(b)数值验证等效模型；(c)通过调制耦合实现慢波系统[52]Fig.6 (a)Schematic diagram of the coupling system;(b)numerical verification of theeffective model;(c)realization of an ultraslow-wave plasmon transport by modulation coupling[52]

3.2 应用：超构表面的角度色散研究与调控

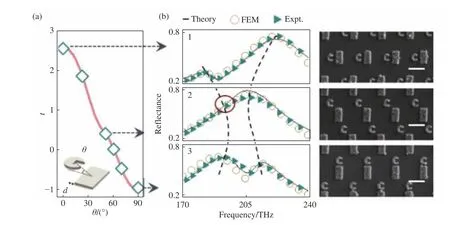
人们在利用超构材料和超表面设计及制备光场调控器件时，发现体系对不同入射角度的电磁（光）波往往表现出非常不一样的电磁响应[56-57]。这种体系电磁响应强依赖于电磁（光）波入射角度的基本特性就是所谓的角度色散。在大多数情况下，体系的角度色散往往表现为体系共振频率随入射角度的偏移，如图7所示。虽然人们早就观测到超构材料中的角度色散现象，但对于其背后的物理机理研究比较少，基本还处于零星孤立的状态，缺乏简单明了的物理图像和准确的理论模型来明确指导体系角度色散的自主调控。

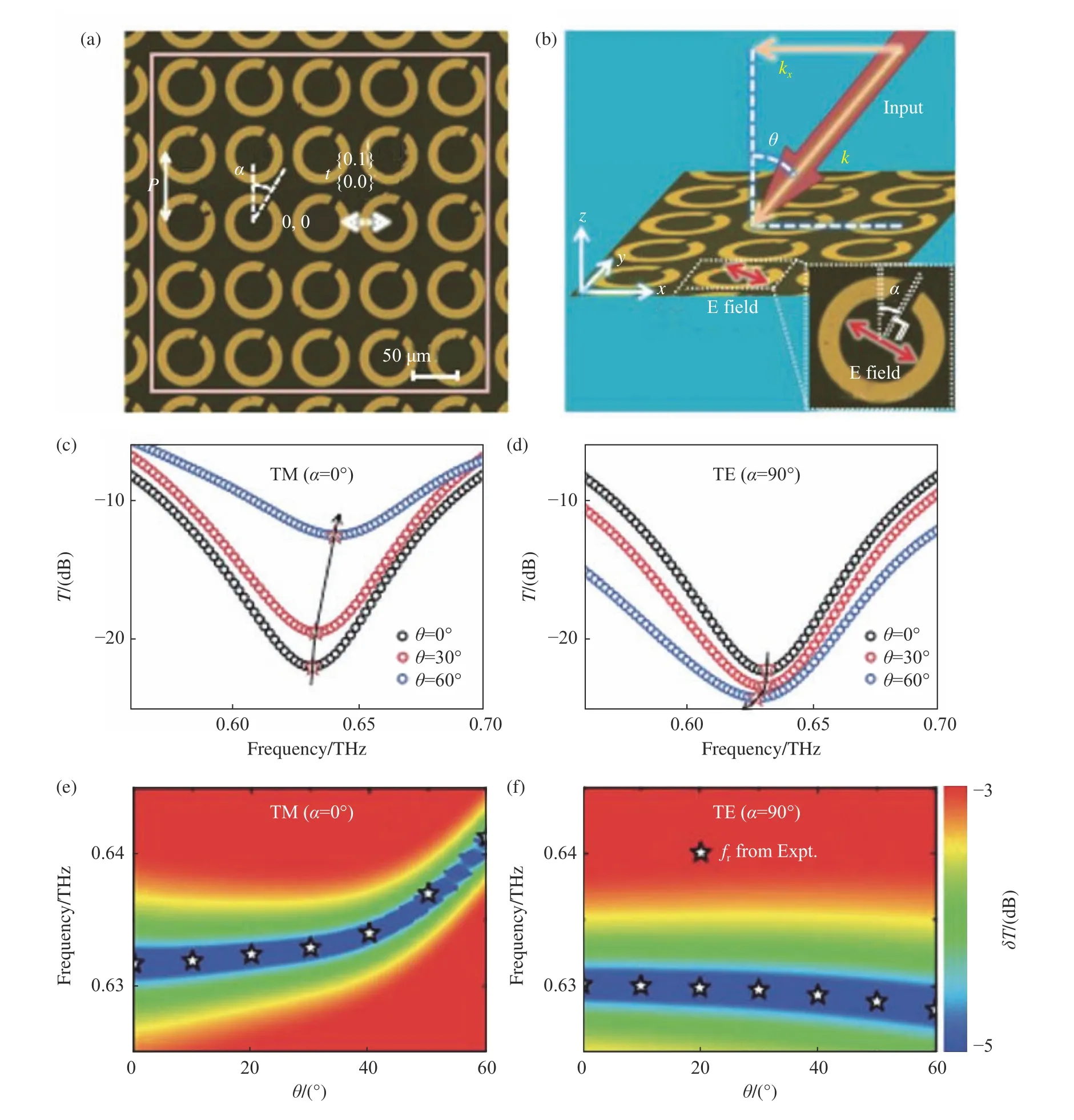
图7 开口环阵列的角度色散现象[56]Fig.7 Angular dispersion of the SRR array[56]

前文建立的紧束缚方法和等效模型，都是对于两体（或有限个体）耦合问题成立的，为了探究超构表面的角度色散来源，需要将两体问题的解推广到周期体系。根据式(13)可写出周期体系任意两个人工原子间的耦合强度:

J0、J1、J2分别代表某个人工原子与行内人工原子的耦合、两行最近邻人工原子之间的耦合以及两行次近邻人工原子之间的耦合；P与k0=ω/c分别代表晶格常数以及入射电磁波在自由空间中的波矢。由此可见，只要获得单个人工原子的波函数就可以直接计算推测体系的角度色散行为。比如，对于THz 波段的开口环结构超构表面，本课题组通过计算开口环之间的耦合强度成功解释了图7中TM偏振波与TE偏振波所激发的共振频率有着完全相反的角度色散行为这一现象[56]。由上述分析可知，由于体系中每一个人工原子都会与周围的所有人工原子发生耦合，因此，孤立人工原子的共振频率会劈裂成一条能带，而不同角度入射的电磁波所激发的模式本质上是能与入射电磁波的平行矢量匹配的Bloch 模式[58]。因此，体系的共振频率会随着晶格内的波矢变化，而两个共振体之间的耦合强度会影响这个变化的幅度。

接下来，将研究谱线Q值的角度色散。考虑金属结构-介质层-金属衬底（MIM）结构的全吸收超表面，通过使用耦合模理论拟合模拟得到的各个入射角照射下的反射率和反射相位，可以得到不同角度入射下的辐射阻尼和吸收阻尼。我们发现吸收阻尼和辐射阻尼均不随角度的变化而变化[59]。这是由于吸收阻尼主要由材料的性质决定，与入射角度无关。而由于MIM 体系所激发的模式是一个典型的磁共振模式，正如第2.1节介绍的那样，共振时上层的金属结构会和最下层的金属层形成沿x方向的反向电流，这一电流回路会激发沿y方向的磁偶极子，而这些磁偶极子在x-z平面的远场辐射是各向同性的。根据耦合模理论，辐射阻尼与模式的远场辐射能力成正比[44-45]，因此辐射阻尼也表现出非常弱的角度依赖性。

以上这些分析清楚地揭示了超构表面中角度色散的物理根源：人工原子之间的近场耦合特性决定了体系共振频率随入射角度的偏移，而人工原子的远场辐射特性决定了体系谱线线形随入射角的变化[59]。这些物理理解为人们提供了两种不同的控制超构表面角度色散行为的方法。

首先，由于超表面共振频率的角度色散行为是由人工原子之间的耦合强度决定的，只需要人为设计超构表面中相邻人工原子之间的耦合强度，就可以自由地控制这个超表面的角度色散强弱。比如，可以通过简单调整人工原子间的位置构型实现体系整体人工原子间的近场耦合强度的最小化，以消除由近场耦合效应引起的共振频率偏移，从而实现入射角度不依赖功能性器件（图8(a)）。

其次，可充分调控角度色散的另外一个重要因素——人工原子的远场辐射。由于体系中的模式为磁偶极子，垂直于入射波的电场偏振方向，体系的远场辐射是各向同性的，因此不管在任何入射角下都能保持辐射阻尼等于吸收阻尼的临界条件。若入射电磁波平行于磁偶极子方向，体系的远场辐射就是各向异性的了，此时只有在特定角度才有可能达到全吸收的临界条件，由此实现了角度选择性的全吸收器件（图8(b)）。

进一步地，可利用体系对TM 和TE偏振光截然不同的角度色散特性来进行设计。超构表面对TE偏振光的共振频率几乎不随入射角度发生变化，而TM 偏振光的共振频率会随入射角的增大发生明显蓝移。因此，在不同入射角度下利用TE和TM 模式间不同反射相位差即可实现角度依赖的多功能偏振调控。基于此原理设计的反射式超构表面可对不同角度入射光实现不同的偏振转化，可将不同角度入射的线偏振分别转换为椭圆偏振，圆偏振或交叉极化偏振等（图8(c)）。

自由调控超表面角度色散的能力也为实现基于非均匀超表面的角度依赖双功能波前调控器件提供了一条新的途径。相比单一的人工原子，可采用更复杂的不全同的长短金属棒结构。这种结构最大的优势就是可以通过自由调节棒的长度L1来控制人工原子的初始相位，并且通过调节L2来调控人工原子间的耦合，从而自由调控角度色散强弱。如图8(d)所示，通过构建一系列具有特定角度色散特性的人工原子，并将其按一定的相位条件分布组合形成非均匀超构表面，即可实现对不同角度入射光的不同波前调控：在正入射情 况下，该超构表面具有反射聚焦功能，而60°斜入射情况下，具备镜面反射功能。

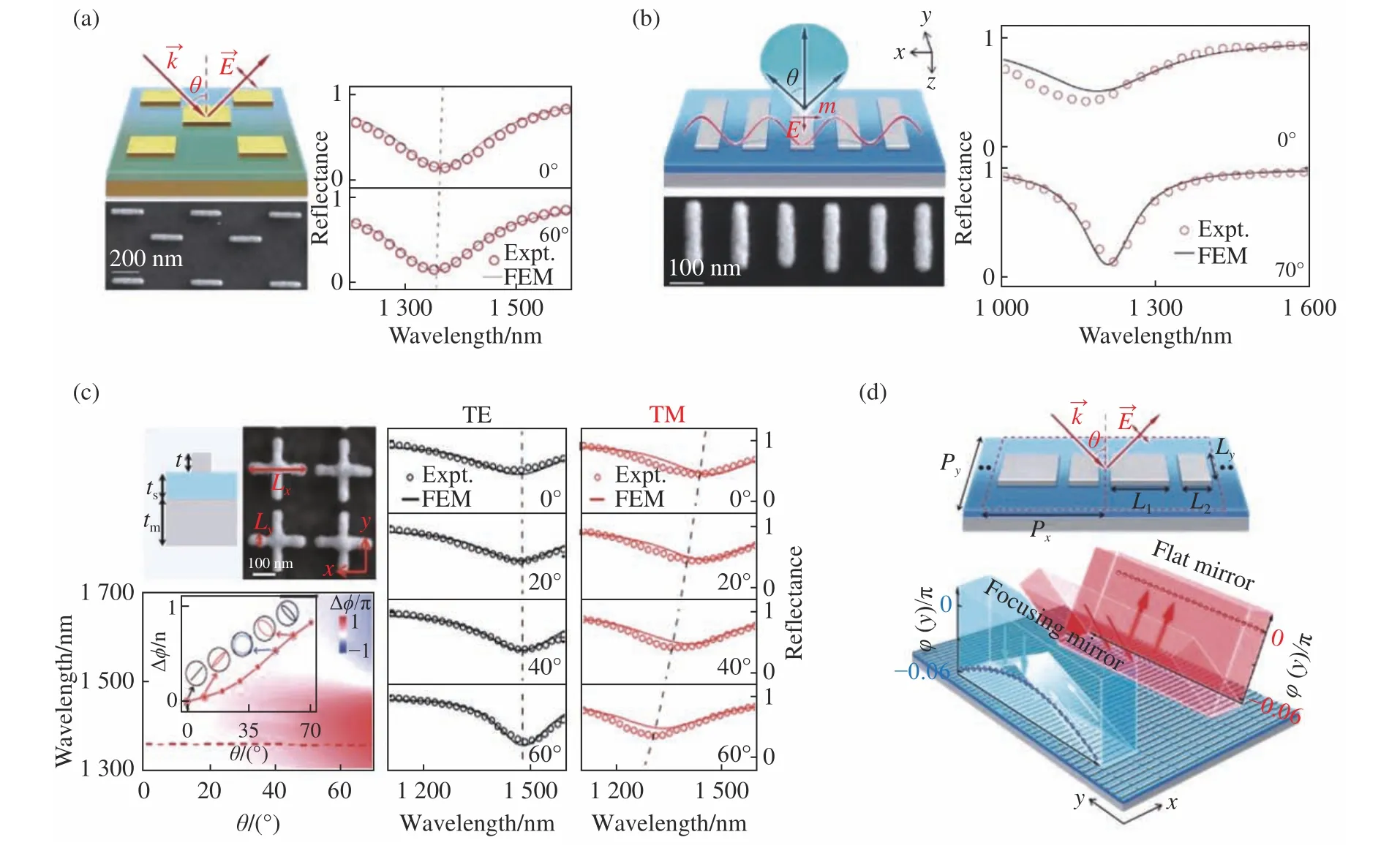
图8 基于调制耦合与辐射实现的(a)无角度色散全吸收器件；(b)角度选择性的全吸收器件；(c)角度依赖的多功能偏振调控器件；(d)非均匀超表面的角度依赖双功能波前调控器件[59]Fig.8 (a)Incident-angle-insensitive meta-absorber；(b)incident-angle-selective meta-absorber；(c)angle-multiplexed metapolarizer ；(d)angle-multiplexed wavefront controller based on modulation coupling and radiation[59]

这一系列研究结果不仅揭示了超构表面中角度色散的物理根源，而且还提出了一条高效自由调控超构表面角度色散的新途径，从而打开了“入射角度”这一全新的调控自由度，极大拓展了超构表面对电磁波的调控能力，为实现更多角度依赖的多功能器件提供了全新的平台。

4 开放体系的耦合理论

4.1 开放体系下模式概念的拓展与泄露本征模的引入

在第三节中，我们建立了在近似封闭体系下的电磁共振体的耦合理论，并在此基础上推导出了将物理图像展示得更为清晰的等效模型。在近似封闭体系的处理方法中，我们将共振体的耗散（包括辐射与吸收）当作微扰来处理，先求解没有吸收的共振结构，然后通过唯象理论拟合结构与环境的耦合参数（即3.2节中用耦合模理论拟合单人工原子辐射强度）。这个处理方式在高Q体系中非常成功（正如前文所验证的那样）。

然而，到目前为止，我们求解的都是“近似封闭体系”问题，所以理论都只能预测共振模式的频率。而实际光学体系中，我们面对的都是开放体系，光学共振体一般都是在一定的外场入射下被激发，然后再辐射到环境中。在实际问题中，除了共振频率外，还有两个非常重要的自由度：共振的辐射能力（反比于模式的品质因数“Q值”）和共振态附近的谱线形状。

虽然物理上光子共振体的耗散性质很容易被接受，但引入电磁场的具有耗散的模式似乎不太直观。事实上，人们通常会提到某谐振器的Q因子，但很少提到电磁场耗散模式的Q因子。这里有一个概念上的问题，严格来说“模式”一词往往对应厄米特征值问题的解，因此开放体系下任何具有耗散的模式似乎不属于这个定义的范畴[60]。由此人们对“模式”的定义进行了拓展，从概念上，将给定微分方程的本征函数定义为“模式”。然而，微分方程本身并不构成一个定义明确的问题，只有通过引入一组边界或辐射条件，才能得到数学问题的一个足够严格的表述，可以称之为“模式”。从这个角度看，封闭体系的模式与开放体系的模式属于不同的种类，因为它们满足不同的边界条件。

例如，在电磁学中，人们将无源麦克斯韦方程组的本征函数集合定义为“模式”，即所谓的准模（QuasiNormal Modes，QNMs[61]），其在无穷远处满足Silver-Müller 辐射条件。此条件下无源麦克斯韦方程组不存在实数频率解，因此准模是一系列具有分立的复数本征频率的“本征模式”。从概念和计算的角度来看，QNM 框架是很有吸引力的，因为在一般情况下，可能没有方法来计算甚至定义一个严格的封闭体系。即使在可以做出这种定义的情况下，与环境的耦合也可能导致大量的频移和波函数畸变。而且基于QNMs的模型构建与微扰闭腔模型相比并不复杂，主要区别在于QNM 框架通常提供了一种明确而精确的方法来计算模型中的各种耦合参数。QNM 广泛地应用于建模纳米光学的真实体系。比如QNMs可用于时域耦合模理论的推导[62]，处理非线性材料[63]，耦合腔波导系统中的QNMs用于微扰理论和Purcell 因子计算[64]等。

QNM方法虽然应用非常广泛，其仍存在一些问题，比如，其对计算资源要求很高，再比如，在数学上，QNM 服从辐射条件而不是边界条件导致了相关概念和计算上的困难，因为辐射条件相对难以处理[60]。常用的PML 截断法则与辐射条件缺乏明确的对应关系。这意味着模式的许多特性没有得到广泛的理解，比如QNMs在大距离下的发散特性。特别值得注意的是，准模理论用于求解人们所关心的多个共振体之间的耦合问题并不高效。由于QNMs并不局域，若直接套用LCAO框架，将导致共振体距离越远交叠积分越大的非物理结果。以一维体系的多层结构耦合问题为例，准模方法主要是通过建立和求解由各个层的QNMs建立的自洽矩阵方程，以找到散射矩阵的极点，运算量很大。

这里我们采用另一种思路定义模式以构建开放体系的总波函数。考虑开放自由空间中存在M个共振体，可由通过N个端口入射的外场激发。该体系的薛定谔方程为：

考虑散射体存在的情况，此时开放体系下每个共振模式的本征波函数不再由求解本征值问题来获取。由此我们引进“泄露本征模”(Leaky Eigen Mode,LEM)的概念[65]。考虑体系只有第m个散射体存在的情况，改变入射波频率，当体系响应最大时，取响应的频率作为“模式”的“本征”频率 ωm，在此入射频率 ωm下 的总场为Ψ(ωm,r˜)，背景场为ΨB(ωm,r˜)，则取总场减去背景场的部分作为LEM 模式场分布:

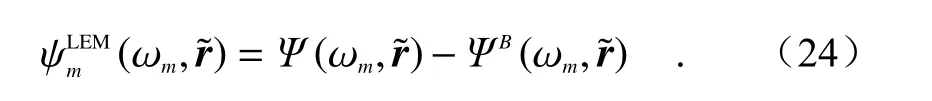
从图9(a)可以看出这个“模式”是带“辐射尾巴”的。当这个“模式”足够局域，即与外界“沟通”的部分足够小(也就是Q值够高)，将总波函数直接减去入射波函数作为“模式”部分就会比较准确，因为此时入射场与其相比是如此之小，以至于可以忽略不计。

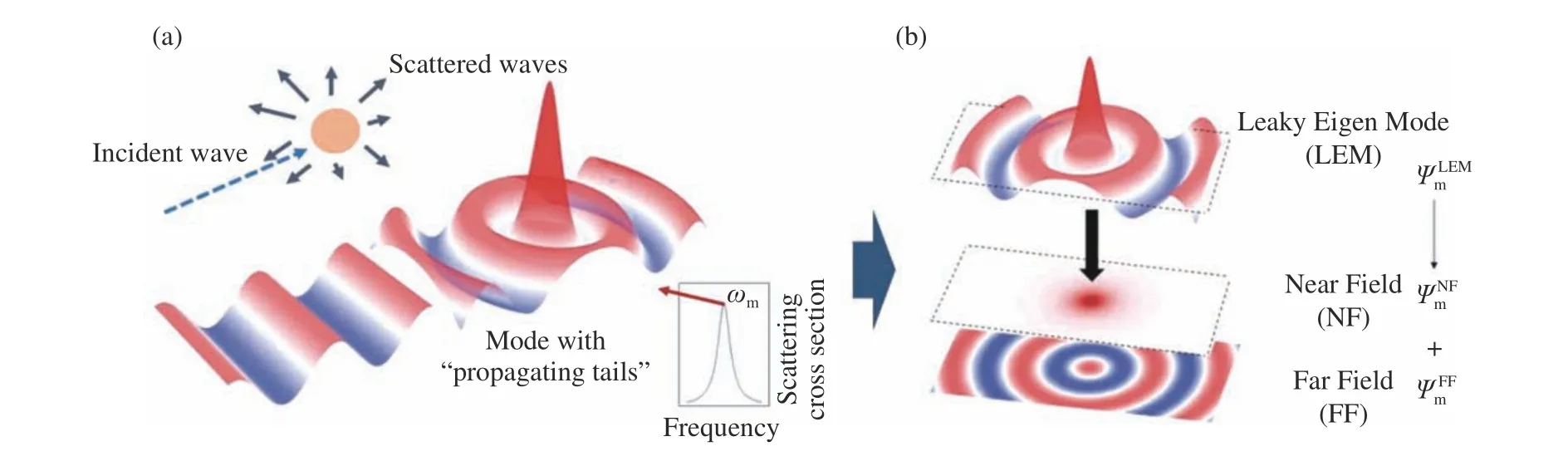
图9 （a）泄露本征模式的获取方式与（b）近远场分离Fig.9 (a)The way to obtain the leaky eigen mode and (b)separation of the near-and far-field

以上模式均为已做好归一化。

值得注意的是，以上所有波函数的场分布都是在共振频率 ωm处得到的。LEM 的本质是一个受迫振动模式，其应该被调整到任意频率 ω。在高Q近似下，我们认为近场部分的场分布不随外场入射频率的变化而变化，仅需要把时谐因子用e−iωt替换掉e−iωmt即可，远场辐射部分则需要做相应调整，除了时谐因子外，还需要用波矢k(ω)替换掉k(ωm)。

从以上分析可以看出，泄露本征模式是在实数频率下获得的，具有实际的物理意义，与准模十分不同。图10直观地展示了二者波函数的不同。

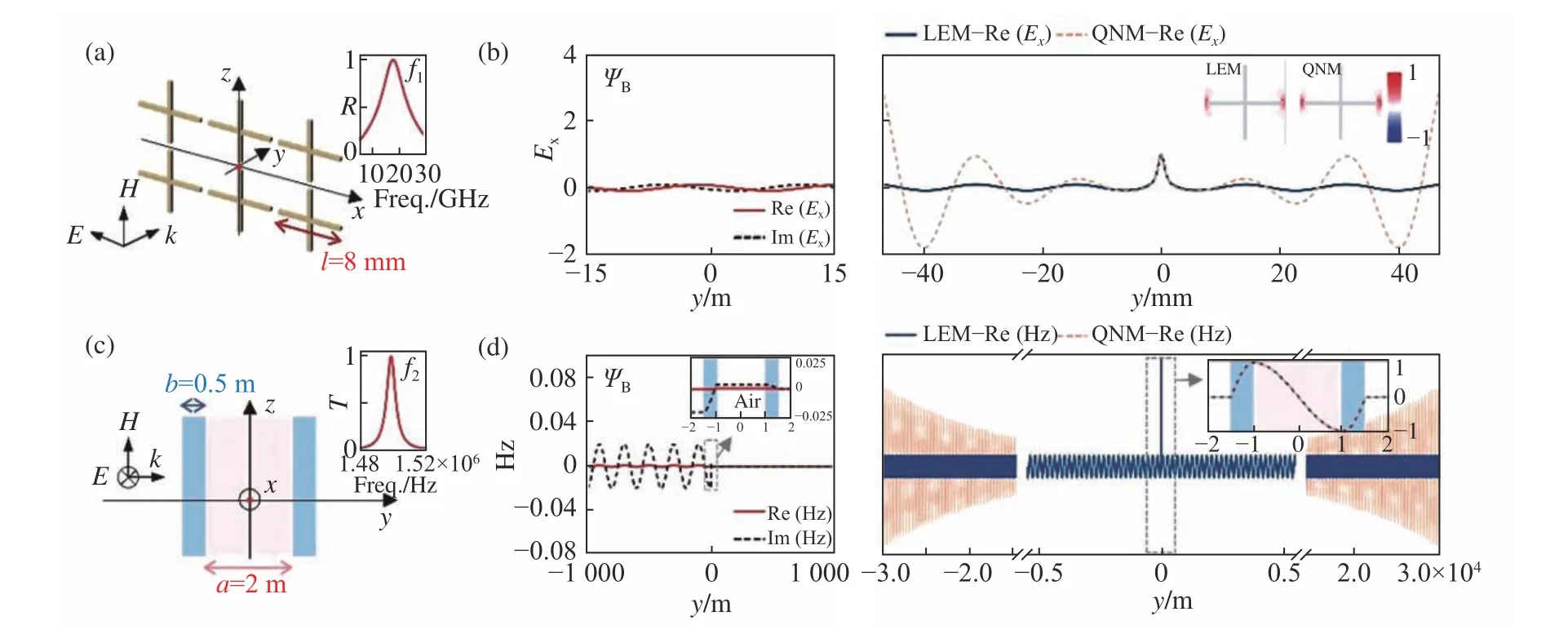
图10 不同体系的泄露本征模式与准模的对比[65]Fig.10 Comparisonsof LEM and QNM for different systems[65]

4.2 基于泄露本征模耦合理论的超构表面调控

C nn′为体系的背景散射矩阵，dnm为模式m对端口n的散射，端口离模式足够远，近场已经衰减完毕，因此可化简。这样就得到了散射方程的具体形式。

式(28)～式(31)构成了开放体系理论的核心内容，描述了开放系统中的模式演化和散射。它们清楚地显示了模式在外部激励下发生受迫振动的物理过程。综上所述，我们建立起了开放体系下的形式耦合理论。对于任何一个给定的体系，只需要其满足高Q近似，原则上都可以将具体的哈密顿量形式与内积形式代入形式耦合理论中，从而获得体系的动力学方程和散射方程。该理论能够准确计算处理模式间的不同耦合方式，包含了近场相互作用和通过辐射通道产生的远场干涉，并给出清晰的物理图像。

耦合理论加深了对于耦合这一现象的物理理解，能够进一步指导调控耦合行为，从而为实现调控响应谱线提供了可能性。原则上只要获得单散射体的泄露本征波函数，便可以计算任意分布的散射体间的耦合，从而预测该耦合体系的光学响应（如透/反射或散射谱）。这启发我们通过设计模式间的耦合强度从而实现对最终谱线线型的设计。

如图11所示，我们以超表面的两模式耦合为例，建立起普适的相图来指导改变所涉及的两个模式之间的耦合，根据实际需要定制耦合光学系统的谱线线形。基于所发展的理论直接计算预测不同相对角度下的两个散射体之间的耦合强度以及其相对应的透反射谱线，建立起结构分布同谱线行为的一一对应关系，从而通过设计散射体耦合实现了对响应谱线线型的设计。

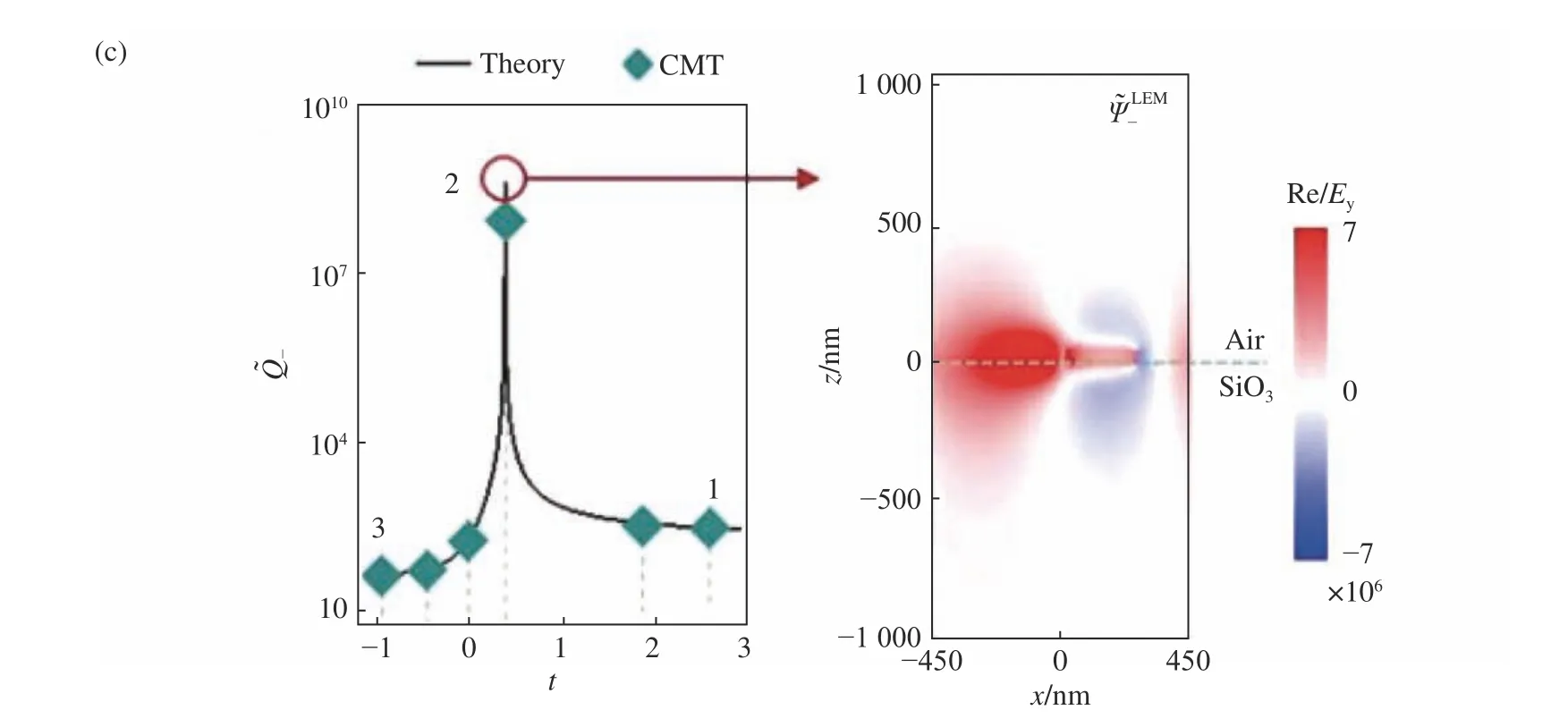
图11 通过控制复杂光子体系的耦合强度实现对谱线线形的自由调控与完全“暗”模式的构建[65]Fig.11 Tailoring of the lineshapesof the coupled plasmonic and achieving BIC by modulating the coupling strength between the resonators[65]

我们发现，在一定条件下，尽管光学共振体自身可能表现出较大的辐射损耗，依然可以通过设计波函数分布以调整模式之间的耦合，从而产生辐射损耗为0的完全“暗”模式，即所谓的BIC(Bound State in Continuum)。所有理论上的预测都通过一系列近红外实验进行了定量验证。

5 总结与展望

超材料设计的关键之一，就是作为人工原子的光子共振体的选择。光子共振体的光响应效率和响应方式基本决定了超材料的效率和功能。因此，对光子共振体的响应研究是超材料研究中十分重要的一环。本文集中讨论了如何处理人工原子的耦合问题。以近似封闭体系为起点，将麦克斯韦方程组改写成了“类薛定谔方程”的形式，将建立好的方程代入量子力学和固体物理中已经发展成熟的处理方法中，建立了色散光学体系下的紧束缚方法。我们进一步以此为基础，进行多极矩展开，得到了具有清晰物理理解的等效模型。在此理论指导下，我们理解了角度色散现象的物理内涵，对角度色散行为的物理挖掘为调控电磁波提供了一个新的自由度，显著扩展了超表面操控电磁波的能力，刺激了角度依赖的多功能元器件的设计和应用。

最后，我们将理论进一步推至开放光学共振体系。通过引入泄露本征模式的概念，可以同时考虑近场与远场的相互作用，并以此作为基础对复杂耦合体系的总波函数进行重新构建。由此，我们从第一性原理出发建立了一个完整的理论框架，其中所有重要的耦合参数都可以直接进行计算而无需拟合，从而使直接预测耦合光子体系的光学响应(包括模式频率和谱线线形)成为可能。

我们建立的耦合理论不仅可以帮助研究人员了解在光子系统中发现的独特光谱线形背后的丰富物理原理，更重要的是，它能作为全新的理论工具来指导设计满足特定需求的光学响应系统，帮助人们实现对于光与物质相互作用的更自由且明确的调制，并且原则上可以该形式扩展到其他类型的波的耦合系统进行研究。该理论为已被广泛使用的耦合模理论提供了扎实的数学物理基础，揭示了耦合模理论中所有经验参数的明确物理含义，同时为研究人员提供了一套强大工具用于理解并调控多共振体间的耦合行为，为按需“设计”耦合光子系统提供了可能。