水库水位变动下库岸滑坡稳定性分析

赵桂兰

(赫章县水务局，贵州 赫章 553200)

0 引 言

滑坡灾害一直是全球三大工程地质问题之一，也是防灾减灾关注的重点，滑坡导致的工程建设问题也给人民群众造成了极大的生命财产损失。因此，目前已有大量学者对边坡稳定性问题展开研究。马崇武[1]等人通过有限元数值模拟方法，将水位变化下的坡体内部渗流场视为准静态，发现其边坡岩土体在饱和之后其抗剪强度大大降低，对应的边坡安全系数同样呈现降低的趋势。刘建军等人通过数值模拟分析方法，结合某区水电站工程概况，研究了该区域蓄水前后边坡地下水渗流场的变化规律。刘新喜等人基于滑坡数学模型，建立二维渗流方程，考虑边坡岩土体的饱和与非饱和因素，研究了水位变化下边坡内部的渗流场变化，最后采用了简布法分析边坡滑塌时的安全系数[1-3]。刘红岩等人利用Geo-Studio有限元分析软件，采用渗流模块对不同水位条件下的边坡浸润线位置进行研究，获得了水位变化下渗流速率以及孔隙水压力变化规律。张文杰等人对比饱和土理论，发现该理论应用于边坡渗流和稳定研究中存在的诸多问题，进而采用饱和-非饱和分析方法进行水位变化下边坡内渗流场变化规律的研究[4-5]。唐辉明以某库区滑坡问题为研究对象，利用有限元数值模拟软件，研究了不同水位变化下边坡渗流场和应力场的变化规律。汪斌通过分析水位变化下边坡失稳的成因机制，并建立某库湾区渗流场和应力场的数值模型，获得了水位变动对边坡稳定性的影响。土泽能等人基于渗透系数法，通过有限元软件进行二次开发，得到了稳定-非稳定渗流分析程序，进而对不同渗流状态下的边坡的渗流场进行了研究[6-8]。

综上所述，本研究将结合某库区工程项目，利用Geo-Studio有限元分析软件，研究在不同水位变化工况下库岸边坡稳定性的变化规律，为现有边坡稳定性设计提供参考依据。

1 工程概况

本研究是以我国江西省某水库项目的边坡为研究对象，该边坡土层组成以风化岩、滑动体和坝基岩为主，简化可得该库岸边坡几何尺寸如图1所示，其对应的岩土体物理力学参数如表1所示。

图1 库岸边坡几何尺寸图

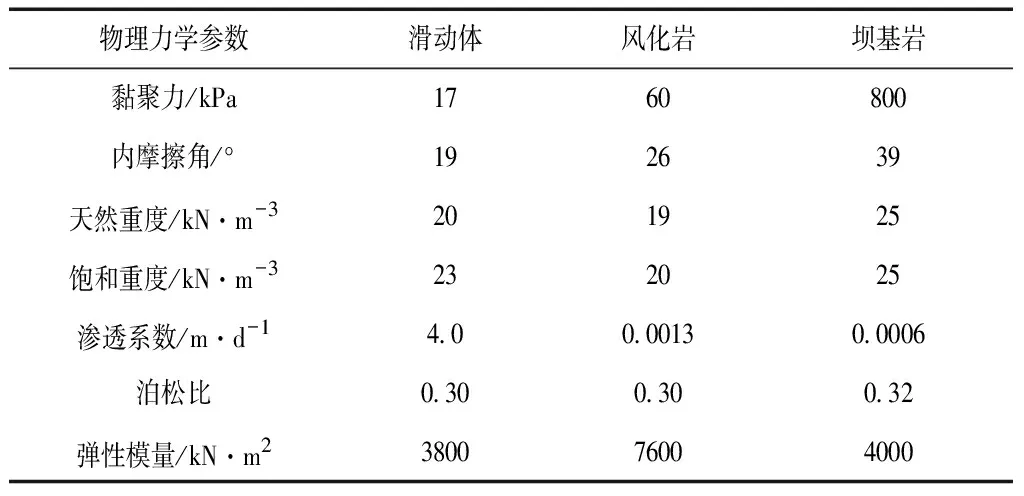
表1 库岸边坡岩土体物理力学参数

2 建立库岸边坡模型

本研究通过利用Geo-studio有限元分析软件，建立库岸边坡模型，采用SWEEP/W模块进行不同水位条件变化下的库岸边坡稳定性研究。该边坡模型以5m水位作为稳定渗流的初始水位条件，边坡右边界25m以下部分定义为变水头条件，其余边界均为零流量边界。本研究通过细化网格提高计算精度，对库岸边坡模型的网格划分如图2所示，其网格节点共2080个，单元共有1992个，相应的边坡模型初始渗流状态和坡体结构如图3和图4。

图2 库岸边坡模型网格划分图

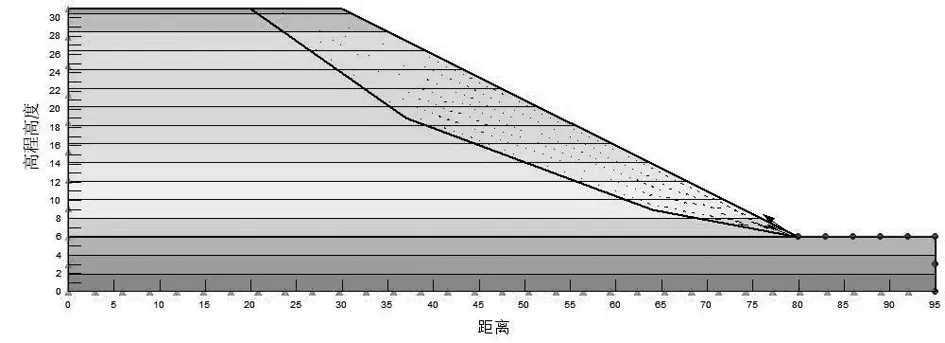
图3 库岸边坡初始渗流场图

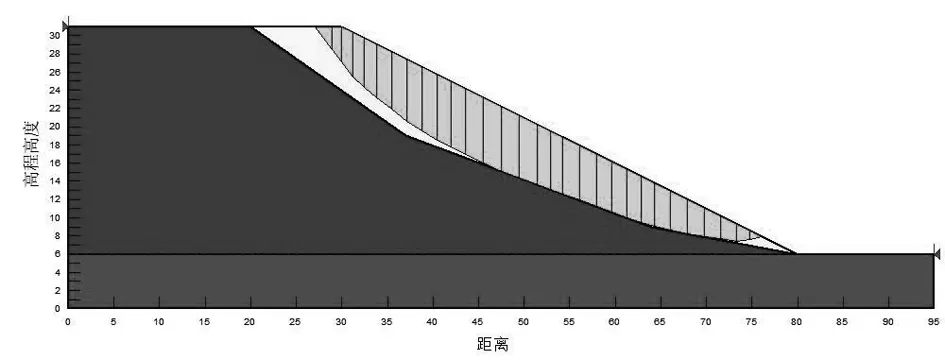
图4 库岸边坡初始条件滑坡图

按照某库区边坡水位实际情况，将水位变化分为水位上升、水位稳定和水位下降阶段，并制定如下有限元模拟试验方案。

表2 有限元模拟试验方案

3 计算结果及分析

本研究以(45,20)，(50,20)，(55,15)，(60,15)，(70,15)，(75,10)，(80,5)7个具有代表性的观测点为研究对象，分别研究分析了在水位上升、水位稳定和水位下降阶段边坡内部孔隙水压力的分布情况。

3.1 孔隙水压力的变化规律

1)水位上升阶段：

由图5和图6可获得在水位上升阶段，边坡内部的孔隙水压力分别在18d和30d里的变化云图。可以发现，当水位上升时，库岸边坡的水位线也逐渐上升；随着水位的不断提升，坡表处的浸润线率先响应，而距离坡表较远的测点响应较慢，且距离越远变化越小；随着浸润时间的持续，浸润线由坡表至坡内深处不断延拓。

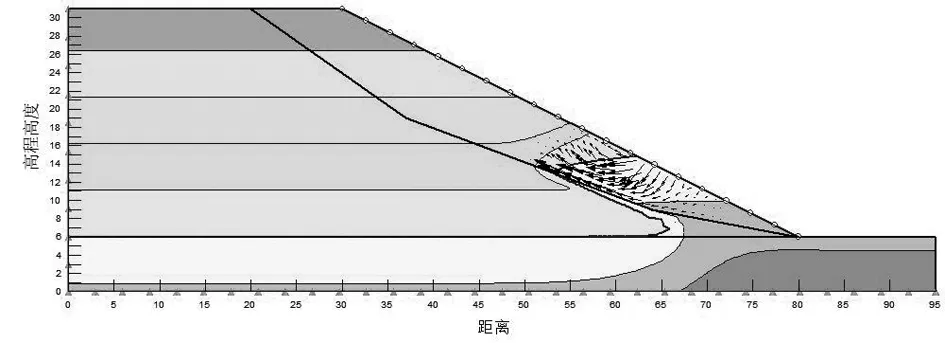
图5 水位上升阶段第 18d 孔隙水压力云图

图6 水位上升阶段第 30d 孔隙水压力云图

随着时间的增加，在水位上升阶段坡表测点的孔隙水压力变化规律如图7所示，可以发现，坡表各个测点的孔隙水压力随着水位的不断提升而渐渐增大，而坡顶与坡脚处的增幅不尽相同。其中，在水位不断上升的过程中，坡顶处测点孔压未出现明显变化，直至水位达到坡顶测点后孔隙水压力呈现出迅速增大后略有降低的现象，最终保持稳定。而坡脚处测点(80,5)则由一开始就呈现出线性增加的趋势，当水位达到25m时，该测点的孔隙水压力达到了175.412kPa。

图7 水位上升阶段坡表测点孔隙水压力变化曲线图

由上图孔隙水压力变化曲线可知，在水位上升阶段水不断入渗坡体，形成了由坡表至坡体内部的渗流，引起了坡体内部浸润线向坡表倾斜的变化规律。由于边坡不同高度的土性不尽相同，从而使得坡体内部的各个部位的浸润线变化速率并非保持一致，存在一定的差异或滞后，且滑动体处的土体渗透性较大，因此该处的浸润线变化显著。

2)水位稳定阶段：

由图8可知，在水位稳定阶段坡体内部浸润线变化缓慢，这是因为随着入渗时间的增加，坡体内部渗流范围增大，渗流路径逐渐由滑动体入渗至风化岩，使得浸润线缓慢抬升。由图9可知在40d后，边坡各测点处孔隙水压力基本保持不变，这是因为在水位稳定阶段边坡内部土体几乎始终保持着饱和状态。

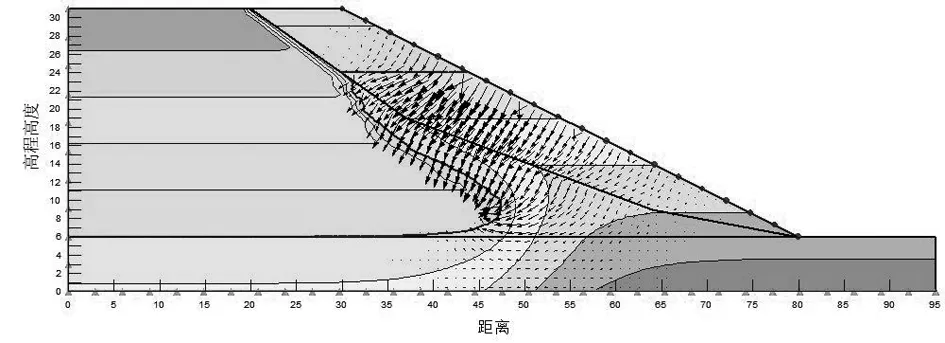
图8 水位稳定阶段第 200d 孔隙水压力分布云图

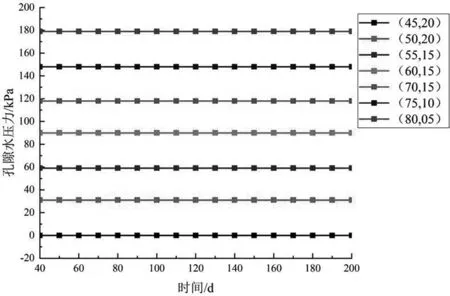
图9 水位稳定阶段坡表测点孔隙水压力变化曲线

3)水位下降阶段：

水位下降阶段坡表测点的孔隙水压力分布云图如图10所示，可以发现，当水位下降时，坡内的浸润线随之下降，但其坡内水位下降速率存在明显的滞后现象，这是由于不同土层的土性不同，对应的渗透系数也不同，因此，渗透性较大的滑动体土层降速要远大于风化岩土层。

图10 库水位下降阶段第236d孔隙水压力分布云图

图11反映了在水位下降阶段坡表各个测点的孔隙水压力的变化情况，可以发现，该工况下边坡土体的孔隙水压力随着水位的降低呈现出先快速减小后趋于稳定的趋势，其快速减小的原因系水位下降导致边坡内外水压差较大，形成了由坡内向坡外的渗流力，加速了孔隙水压力的消散，当水位趋于稳定时，相应的孔隙水压力也渐渐稳定下来。

图11 水位下降阶段坡面点的孔隙水压力变化图

3.2 水位变化过程的稳定性分析

将水位变化全过程中的渗流计算结果导入至稳定性分析模块中，可得不同工况下不同时刻的稳定性变化图(如图12-16所示)。

图12 水位在初始状态的滑坡图

图13 水位上升阶段第 36d 的滑坡图

图14 水位稳定阶段第 200d 的滑坡图

图15 水位下降阶段第 236d 的滑坡图

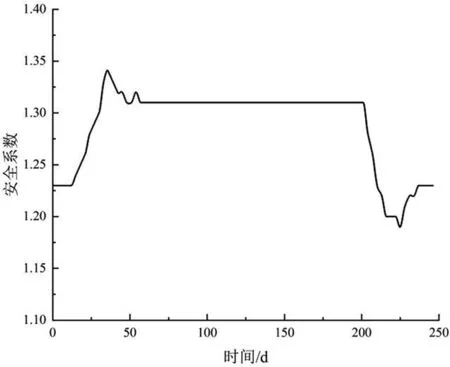
图16 库水位升降过程安全系数随时间的变化曲线图

由图可知，在水位上升阶段，边坡的呈现出略微减小而后逐渐增大的规律，其中当水位达到25m时，相应的边坡安全系数达到最大值；在进入水位稳定阶段后，随着时间的持续增加，库岸边坡的安全系数逐渐减小，当时间积累至一定值后，边坡安全系数保持稳定；当进入水位下降阶段时，边坡安全系数出现明显的骤降，随着水位的持续下降，其值达到最小值并逐渐趋于稳定[9-10]。

究其原因，在水位上升阶段初期，渗流首先从边坡坡脚开始，使得坡脚处土体孔隙水压力逐渐增大，也意味着该处岩土体的抗剪强度逐渐减小。并且，由于坡脚处坡面内外形成水头压力差，对库岸边坡的稳定性造成影响，因此在水位上升阶段初期出现短时间的安全系数减小现象；随着水位持续上升并达到一定高度时，由于坡体侧外水位线总是略高于坡内侧，形成了由坡外指向坡内的压力，在一定程度上提高了边坡的稳定性；同时，坡体内部浸润线随着时间的持续增加而逐步提升，并渐渐渗入边坡土体深处，坡体内外压力差也逐渐减小，而坡体内孔隙水压力随之增大，这也表征着此时边坡土体抗剪强度的减小，进而导致安全系数降低；在水位稳定阶段，边坡内外浸润线高度保持一致，使得坡体内外压力差减小为0，孔隙水压力达到最大值并且稳定，因此边坡安全系数稳定不变；在水位下降阶段，由于水位的下降导致坡体内外平衡状态改变，此时由于坡体内部水位线高于坡外且存在滞后现象，渗透力转由边坡内侧指向外侧，对其稳定性造成影响，直接导致边坡安全系数的降低；当水位下降至5m时，坡体内外水位线基本达到一致，且坡内孔隙水压力消散完全并达到一定的平衡，其安全系数表现为先有一定的提升而后趋于稳定[11]。

4 结 论

通过对水库水位变动下库岸滑坡稳定性的分析，得到的主要结论如下：

1)随着水位的不断提升，坡表处的浸润线率先响应，而距离坡表较远的测点响应较慢，且距离越远变化越小，随着浸润时间的持续，浸润线由坡表至坡内深处不断延拓。

2)由于边坡不同高度的土性不尽相同，从而使得坡体内部的各个部位的浸润线变化速率并非保持一致，存在一定的差异或滞后，且滑动体处的土体渗透性较大，因此该处的浸润线变化显著[12]。

3)在水位下降阶段，由于水位的下降导致坡体内外平衡状态改变，坡体内部水位线高于坡外且存在滞后现象，渗透力转由边坡内侧指向外侧，直接导致边坡安全系数的降低。

4)当水位下降至5m时，坡体内外水位线基本达到一致，且坡内孔隙水压力消散完全并达到一定的平衡，其安全系数会表现为先有一定的提升而后趋于稳定。