主从式上肢外骨骼康复机器人的运动学研究

鲁守银， 张蔚然， 赵洪华

(1. 山东建筑大学 信息与电气工程学院， 山东 济南 250101； 2. 积成电子股份有限公司， 山东 济南 250100；3. 济南大学 机械工程学院, 山东 济南 250022)

由脑卒中引起的偏瘫造成许多患者行动不便、卧床不起和生活不能自理等问题，严重影响了患者及其家人的正常生活[1]，需要进行及时、有效的治疗。除了药物治疗外，目前医疗界普遍采用的方法为物理治疗，即通过运动训练、活动关节等手段使患者肌力得到提升，达到康复目的[2]。随着医疗设备与人工智能的不断发展，针对偏瘫治疗的穿戴式机器人与系统成为研究热点，许多学者、企事业单位在偏瘫患者运动康复方面进行大量工作，取得了一些成果[3]，为运动康复提供了技术支持。

目前， 国内针对治疗与运动康复的上肢外骨骼机器人以单臂形式为主， 获取患肢肌力与肌电信号为控制信号进行单臂的运动控制[4-5]。 以肌力与肌电为控制信号的单臂康复机器人存在控制信号获取困难、 特征分析精准度有待提高等问题。 本文中采用符合人体上肢运动规律的主从式结构，作为设计基础， 利用患者健康侧上肢的运动功能作为控制输入信号； 基于主从式结构，利用齐次坐标[6]建立机器人主从臂在统一固定坐标系下的运动学方程； 通过运动学方程计算主从双臂极限位置时互不干涉的安全距离， 以人体上肢活动规律与中国成年人平均臂长为基础， 在保证主从双臂互不干涉的安全距离条件下设计双臂各5个自由度的主从式上肢外骨骼康复机器人。

1 运动学分析

1.1 人体上肢参数

机器人的机械结构主要有上肢左、右双臂和底座3个部分。机器人采取主从双臂结构，主从双臂为同构对称形式，各臂均有5个自由度。主从左、右双臂均可实现肩部的水平面内外旋转和矢状面的屈伸动作、肘部的屈伸与前后转动以及腕部侧偏摆动。底座主要包括座椅和控制柜等。开展主从式上肢外骨骼康复机器人的运动学研究，必须了解人体上肢的参数与各关节运动范围，从而保证主从式上肢外骨骼符合人体上肢运动形式，使得主从式上肢康复机器人更加“拟人”，完成的训练任务更有针对性，人体手臂各关节运动范围如表1[7-8]所示。

表1 人体手臂各关节运动范围[7-8]

1.2 运动学分析

为了满足人体仿生学，主从式上肢外骨骼康复机器人为左、 右双臂同型同构结构，双臂均有肩部活动关节、肘部活动关节和腕部活动关节，符合人体工学原理。利用Denavit-Hartenberg(D-H)参数建模法建立主从式上肢外骨骼康复机器人双臂几何模型，如图1所示，其中Os1(Os2)为从臂第1、 2肩关节重合的中心点，Os3(Os4)为从臂第3、 4肘关节重合的中心点，Os5(Os6)为从臂腕部第5、 6关节重合的中心点，Os1Os3(Os2Os4)为大臂杆件， 长度为L1，Os3Os5(Os4Os6)为小臂杆件，长度为L2，主臂类似表示，不再赘述；Smi(Omi-XmiYmiZmi)、Ssi(Osi-XsiYsiZsi)，i=1,2,…,6， 分别为以主、 从臂各关节中心点为原点的各关节活动坐标系。

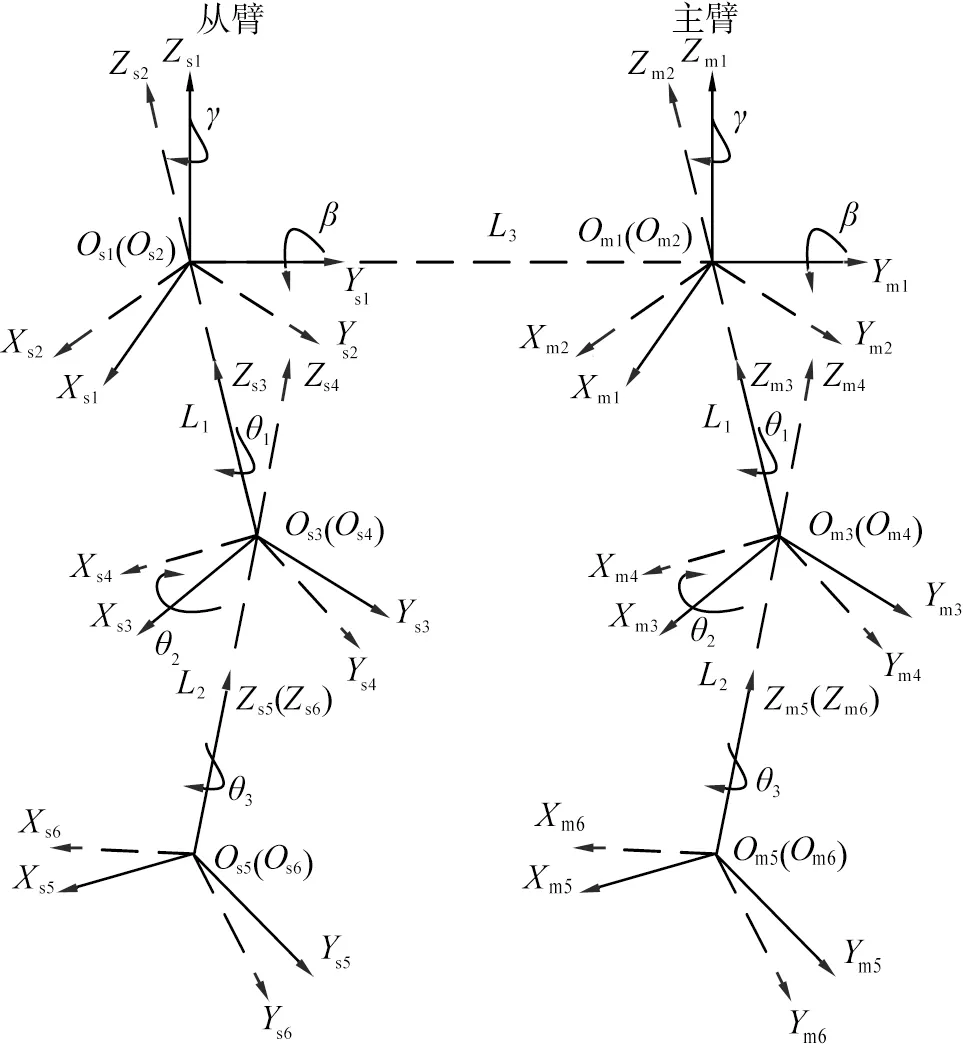
Omi-XmiYmiZmi、 Osi-XsiYsiZsi—主从臂各关节中心点为原点的各关节活动坐标系，i=1,2,…,6； L1—机器人大臂长度； L2—机器人小臂长度； L3—机器人主臂、从臂间距； γ、 β—机器人肩关节水平面、 矢状面屈伸角度； θ1、 θ2—机器人肘关节旋转、 屈伸角度； θ3—机器人腕关节屈伸角度。

利用齐次坐标方程，对机器人运动学进行分析[9-10]。以从臂肩关节中心点Os1为原点，以垂直地面向上为Zs1正方向，以从臂肩关节中心点Os1至主臂肩关节中心点Om1的方向为Ys1正方向，以用户面部正前方为Xs1正方向，建立坐标系Ss1。令Ss1为固定坐标系，Ss3为从臂肘关节动坐标系，从臂肩关节坐标系Ss1到肘关节的坐标系Ss3作如下变化：令坐标系Ss1围绕Zs1轴作角度为γ的旋转，再沿Ys1轴作角度为β的转动，可得辅助坐标系Ss2，这样就完成了绕Zs1轴的内(外)旋肩部转动动作和Ys1轴的肩部屈伸动作，再沿辅助坐标系Ss2的轴Zs2平移L1，则可得到肘部坐标系Ss3，此过程可描述上肢大臂杆件的位姿运动学建模过程。令肘部坐标系Ss3绕轴Zs3转动角度为θ1，再绕Xs3轴旋转角度θ2，可得辅助坐标系Ss4，则肘部可完成依Zs3轴的屈伸动作与绕Xs3轴的内外转动动作，再沿Zs4轴平移L2，可以得到从臂腕部坐标系Ss5，此过程为上肢小臂的位置变化。最后，由坐标系Ss5沿Zs5轴旋转θ3得坐标系Ss6，此过程为从臂腕关节的侧偏动作。主臂肩关节动坐标系Sm1由从臂肩关节固定坐标系Ss1沿Ys1轴平移距离L3而得，Om1(Om2)为主臂肩部第1、 2关节重合的中心点，L3为主、从臂肩关节中心点之间的距离。由于主、 从臂为同型同构，因此主臂各关节运动变化与从臂一致，依次可得主臂运动位姿。至此，主、 从臂所有关节在同一坐标系中表示。

根据从臂肩关节初始位置到上肢大臂的变化，坐标系Ss1绕Zs1轴和Ys1轴分别旋转角度γ、β后，坐标系Ss2的变换矩阵为Ts01，

Ts01=Rot(y,β)Rot(z,γ)=

(1)

式中：c=cos；s=sin；Rot(·,·)为机器人刚体运动绕y、z轴的旋转变换。

powerGUN铝点焊自动焊钳采用一个或者并联两个变压器，用于高电流和高节拍焊接；增大了次级回路元件截面积；优化了冷却水系统，提高了焊钳的冷却散热能力；高强度铝合金结构增加了焊钳的刚性，独立平衡补偿、伺服电动机驱动和压力传感器保证焊接质量，再配合HWH/NIMAK组合控制柜，让其更完美地达到了焊接过程的控制。

肩部旋转后坐标系Ss2由肘关节平移L1后至坐标系Ss3的变换矩阵为Ts12，

(2)

式中Trans(·,·)为机器人刚体运动绕z轴的平移变换。

当屈伸动作从臂肘关节坐标系Ss3沿Zs3轴旋转θ1，再沿Xs3轴的肘部由内向外旋转θ2角度至肘关节时，坐标系Ss4的变换矩阵为Ts23，

Ts23=Rot(z,θ1)Rot(y,θ2)=

(3)

从臂肩关节初始位置坐标系Ss1至肘关节坐标系Ss4的变换矩阵为Ts03，

Ts03=Ts02Ts23=

(4)

从臂肘关节坐标系Ss4至从臂腕关节Ss5的变换矩阵为Ts34,

(5)

从臂腕关节进行屈伸运动，坐标系Ss5旋转θ3后至坐标系Ss6的变换矩阵为Ts45，

(6)

从臂肩关节初始位置坐标系Ss1至腕关节，可得坐标系Ss6的变换矩阵为Ts05,

Ts05=Ts01Ts12Ts23Ts34Ts45=

(7)

最终，从臂腕关节末端坐标在坐标系Ss6中可表示为

(xs6ys6zs61)T，在坐标系Ss1中的坐标点可表示为

(xs1ys1zs11)T=Ts05(xs6ys6zs61)T。

由从臂肩关节坐标系Ss1沿Ys1轴平移距离L3得到主臂肩关节坐标系Sm1，Sm1的变换矩阵为Tm01，

(8)

经过Tm01变换后，坐标系Sm1的原点位于主臂肩关节中心点Om1处。 由于主、 从双臂为同型同构设计， 主臂的动作变化过程与从臂一致， 因此不再赘述计算过程， 仅列出各关节运动动作后相对于固定坐标系Ss1的变换矩阵。

主臂肩关节完成肩部矢状面屈伸和水平面内外旋运动后， 相对于固定坐标系Ss1，变换矩阵为Tm-shoulder，

(9)

主臂肘关节完成肘部屈伸与旋前旋后运动后，相对于固定坐标系Ss1变换矩阵为Tm-elbow，

Tm-elbow=

(10)

主臂腕关节完成腕部侧偏运动后，相对于固定坐标系Ss1，变换矩阵为Tm-wrist，因此，主臂末端活动空间中的所有点均可在固定坐标系Ss1中由Tm-rist表示，即

(11)

2 主从双臂互不干涉分析

在双臂协同进行主从训练过程中，存在双臂干涉问题，尤其存在于双臂的小臂处。例如：机器人在肘部向内弯曲、肩部向内旋运动时，双臂末端腕关节处在空间位置上最接近，造成主从臂相互干涉从而双臂均运动不到目标位置，影响运动康复训练的效果，当有严重碰撞时，还会对患肢造成二次伤害。由此可知，在设计时，干涉问题需要解决，因此以人体上肢关节活动最大角度作为边界条件进行分析。

双臂运动范围及产生干涉时极限位置的简化几何模型如图2所示。由图可知，在根据人体上肢设计大臂杆长L1、 小臂杆长L2一定的情况下，如果双臂不存在干涉，需要对双臂间距L3进行分析计算。由图1可知，主、从臂各关节的空间位置均可以在固定坐标系Ss1中表示出来， 通过计算在固定坐标系Ss1中的关节坐标不重合的点，进而推算出L3的合理值，则可避免干涉问题。

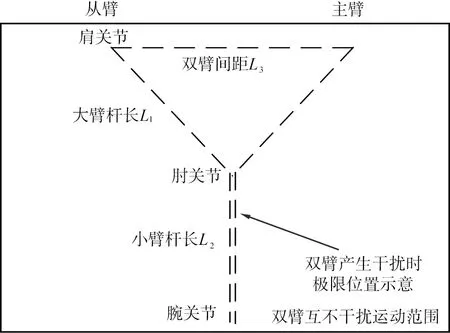
图2 主、 从双臂运动范围及产生干涉时极限位置的简化几何模型

干涉问题主要存在于双臂的小臂杆处，如果保证主、 从臂肘关节和末端腕关节在运动时不干涉，则可有效避免双臂的干涉。

在主、 从臂的运动过程中， 当肩部在水平面内旋至最大位置(γ=120°)时， 双臂肘关节最接近， 分别取主、 从臂肘关节中心点坐标为(xm4ym4zm41)T=(0 0 0 1)， (xs4ys4zs41)T=(0 0 0 1)，主臂肘关节中心点坐标通过变换Tm-elbow至固定坐标系Ss1中为

p1=(cγsβL1sγsβL1+L3cβL11)T

。

(12)

从臂肘关节中心点坐标通过变换Ts03至固定坐标系Ss1中为

p2=(sβL10cβL11)T

。

(13)

图3 不同情况下主、 从臂肩关节中心点之间距离 L3的取值

在主从臂运动过程中， 只有肩部在水平面内旋(角度为γ)和肘部内屈(角度为θ1)均至最大位置时(γ=120°，θ1=150°)， 会造成双臂末端腕关节处的干涉， 与肘关节旋内旋外角度θ2和腕关节侧偏角度θ3无关。 为了方便计算，θ2、θ3均取为0°， 取主、 从臂末端腕关节中心点坐标分别为(xm6ym6zm61)T=(0 0 0 1)， (xs6ys6zs61)T=(0 0 0 1)， 主臂末端腕关节中心点坐标在固定坐标系Ss1中表示为

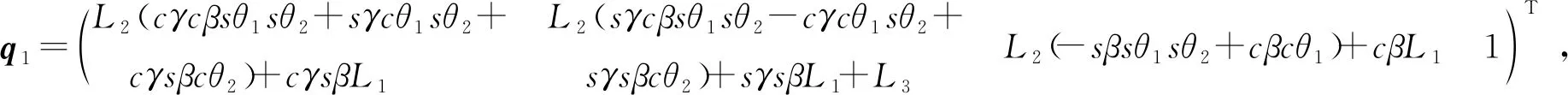
(14)

从臂末端腕关节中心点坐标在固定坐标系Ss1中可表示为

(15)

综上，双臂不出现干涉问题的条件为

(16)

(a)三维图

3 整体结构设计与主从训练方法

主从式上肢外骨骼康复机器人可用于偏瘫患者恢复其上肢运动功能。在运动训练过程中，患者通过健肢可运动侧穿戴主臂，通过患肢康复侧穿戴从臂。在训练时，患者通过健肢运动带动主臂运动，主臂安装有压力传感器量化为运动意图，主臂各关节运动位置作为从臂各关节运动目标位置。控制系统根据目标位置和运动意图，实时控制从臂各关节电机角位移和输出力矩，实现从臂跟随主臂运动。机器人从臂运动至目标位置，带动患者患肢运动，从而使得患者健康侧肢体与患病肢体两侧肢体协同运动，完成康复任务。患肢得到训练，肌力得到提升。整个训练过程对偏瘫患者的康复有积极作用[12-13]。

本文中主从式上肢外骨骼康复机器人为主、 从臂同型同构结构，主、 从臂各5个自由度，其中2个活动关节可实现肩部的矢状面屈伸(关节B)以及肩部的水平面内外旋(关节A)动作，肘部有2个活动关节可实现小臂的屈伸(关节D)与小臂摆动(关节C)动作，腕部的1个关节可以实现手部的摆动侧偏(关节E)运动。 此设计可使患者患肢完成基本的康复任务或简单的日常动作。为了使主从双臂互不干涉，设计间距应满足式(16)，主、 从臂各关节活动范围应满足表1中的要求。从臂采用噪音小、控制精度高的电动驱动方式， 通过电机与中间减速器相连，降低末端输出的转速，从而带动外骨骼机械臂关节转动。采取主从控制方式，以主臂各关节的运动角度作为从臂的各关节运动目标位置，主臂各关节安装有角位移传感器。为了防止二次伤害，保护患肢的安全性，在从臂的各关节安装了限位开关。主从式上肢外骨骼康复机器人设计结构如图5所示，现场训练如图6所示。

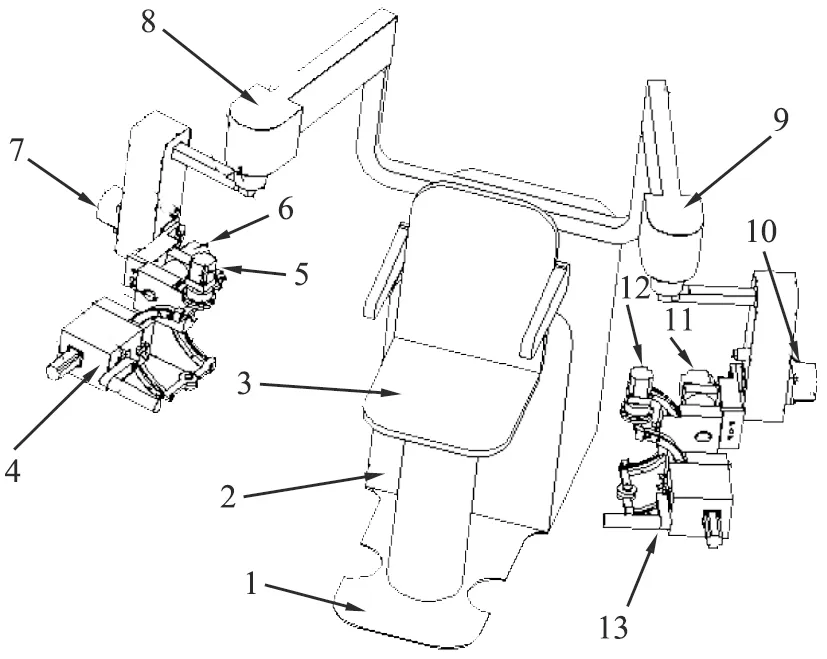
1—基座； 2—控制柜； 3—座椅； 4—8—机器人主臂； 9—13—机器人从臂； 8、 9—主臂和从臂肩部水平面内外旋关节；7、 10—主臂和从臂肩部矢状面屈伸关节； 6、 11—主臂和从臂肘部的转动关节； 5、 12—主臂和从臂肘部屈伸关节； 4、 13—主臂和从臂腕部的摆动关节。

图6 主从式上肢外骨骼康复机器人现场训练图

现场试验中，从臂跟随主臂动作的运动轨迹是通过计算机编程语言C#编写的上位机程序对底层运动控制器Trio获取的角度传感器进行读取并记录的，从臂的各关节跟随主臂动作的变化曲线如图7所示。在主、 从臂的跟随运动过程中，随动效果受主臂关节运动信息采集过程的干扰较大。为了减小主臂运动信息干扰的影响，增加主臂关节活动阻尼，增大主从随动比例因子，缩小从臂的活动空间。通过增大主臂关节活动阻尼，减少相应关节的扰动，通过增大相应关节主从随动比例因子，减小主臂扰动对从臂的影响。由图7可知，从臂各关节跟随主臂意图运动效果良好，跟随精度高，系统响应快。

图7 从臂各关节跟随主臂变化曲线

4 结语

本文中利用齐次方程建立了主从式上肢外骨骼康复机器人运动学模型，使主、 从臂各关节可在同一固定坐标系中进行表示；利用建立的运动学模型，分析主、 从臂末端腕部不干涉的空间位置，并利用蒙特卡罗方法进行了仿真，为双臂间距优化提供了设计依据；设计主、 从双臂各5个自由度的上肢外骨骼康复机器人机构，并给出从臂跟随主臂运动意图的训练方法，可使训练时运动轨迹更平滑，从而保证训练效果与安全性。