回填土夯实效果与挡墙高度对加固边坡失效概率的影响

王上上， 陈 富， 翟 明， 刘 旭， 李 亮， 凌贤长

(青岛理工大学 土木工程学院， 山东 青岛 266033)

在铁路、公路、水利、房建等建设工程中，边坡失稳产生的问题的影响越来越严重，边坡安全系数评估已成为工程地质和岩土工程领域的重要问题之一，通过评估边坡稳定性进而对危险边坡采取加固措施一直是岩土工程领域的研究热点[1-4]。现阶段，边坡稳定分析方法主要有以有限元法[5-7]、边界元法[8]、离散单元法[9]为基础的数值分析法和以刚体极限平衡理论为基础的极限平衡法[10-12]。极限平衡法可给出物理意义明确的边坡稳定安全系数及可能的破坏面，力学模型简单，受到岩土工程界的青睐。Duncan[13]对比几种极限平衡法，如Spencer法、Janbu法、 Morgenstern-Price法，结果表明，所得安全系数间的差异不超过12%，在工程允许范围之内。Blatz等[14]提出通用两段式楔型极限平衡法研究加筋土坡的稳定性，结果表明，该方法可用于预测无加筋路堤和加筋路堤的崩塌。基于安全系数的边坡确定性分析无法考虑边坡岩土体的天然变异性，因此，国内外工程领域的学者采用可靠度分析[15-16]研究岩土体的变异性。Li等[17]基于二阶多项式的响应面对空间可变土坡可靠度的研究结果表明，从多个响应面得到的逼近值与通过搜索大量潜在滑移面得到的逼近值吻合较好。Dyson等[18]采用有限元法开展了边坡可靠度分析，结果表明，当土质本身不均匀或岩土参数的可靠性很大程度上未知时，概率边坡稳定性分析通常比确定性方法更可取。王旭等[19]、陈昌富等[20]利用Morgenstern-Price法对土坡可靠度分析进行研究，结果表明, 利用可靠度方法得到的可靠度、 破坏概率等指标能够定量描述各参数变异性对边坡稳定性的影响。Oka等[21]、Chowdhury等[22]指出，在边坡可靠度分析中应合理考虑边坡多失效模式，并采用Ditlevsen上、下限法进行边坡系统可靠度分析，得出边坡系统失效概率的可能变化范围。Low等[23]采用一阶可靠度法(first order reliability method, FORM)结合Ditlevsen上、下限法计算边坡系统失效概率。已有研究大多仅得到边坡的失效概率，对边坡加固措施的效果性验证不够全面。为了最大限度地减少边坡失稳对铁路运营的影响，本文中针对哈佳铁路加固边坡进行可靠度分析和加固措施优化，对挡土墙高度进行研究。

1 边坡稳定可靠度分析

1.1 极限平衡法

极限平衡法的主要思想是假定岩土体破坏是由滑体内滑面上发生滑动造成的。在求解安全系数Fs时，首先假设滑动面，并将滑动面与边坡面包围的滑动体看作刚体，不考虑该滑动体变形，将滑动体分为若干竖向条块，通过引入不同假定，计算该滑动面上的Fs。变换不同的滑动面，可以得到不同的Fs值，其中Fs值最小的滑面为最危险滑动面，对应的安全系数即为该边坡稳定的安全系数。基于引入的不同假定，形成不同的极限平衡法，譬如瑞典法[24]、简化Bishop法[25]、Morgenstern-Price法等。

1.2 边坡失效概率计算

1.2.1 边坡稳定极限状态函数

在基于安全系数的极限平衡法中，边坡的极限状态平衡函数为

G=Fs(X)-1=0

，

(1)

式中：G为极限状态函数；X=X1,X2,…,Xw,其中w为变量个数，Xi为安全系数Fs计算所需的第i(i=1,2,…,w)个变量， 如土体的黏聚力c和内摩擦角φ等。本文中采用Geo-Studio软件中的Slope/W模块求解安全系数，滑动面的安全系数Fs采用Morgenstern-Price法进行计算。

1.2.2 蒙特卡罗方法

蒙特卡罗方法是一种基于概率论思想，对随机变量进行数理统计实验及分布概率模拟，从而近似求得预测值的方法，又称为概率统计法[26]。若已知状态变量的概率分布, 对于式(1)所示的极限状态函数，利用蒙特卡罗模拟法，从各随机变量中随机抽取一个样本点，形成一组样本x1，x2，…，xN，其中N为样本个数， 由式(1)计算各样本的状态函数值， 重复N次， 可得到G1，G2， …，GN。 若Gl<0 (l=1,2,…,N)，则称xl为失效样本。 统计失效样本个数M， 则边坡的失效概率pf为

(2)

式(2)即为利用蒙特卡罗法直接计算的失稳概率。

1.3 基于Win-BatchTM语言的失效概率计算

在选取基本变量时，选择变异性较大并且对计算结果影响权重较大的黏聚力c和内摩擦角φ2个参数作为可靠度分析的基本变量。为了简化计算，将变异性较小并且对计算结果影响小的参数(如岩土容重、剖面几何参数等)作为定值进行处理。在计算失效概率过程中，假设基本变量黏聚力c和内摩擦角φ相互独立，服从对数正态分布。本文中提出的基于Win-BatchTM语言的失效概率计算分析方法的计算流程如图1所示。

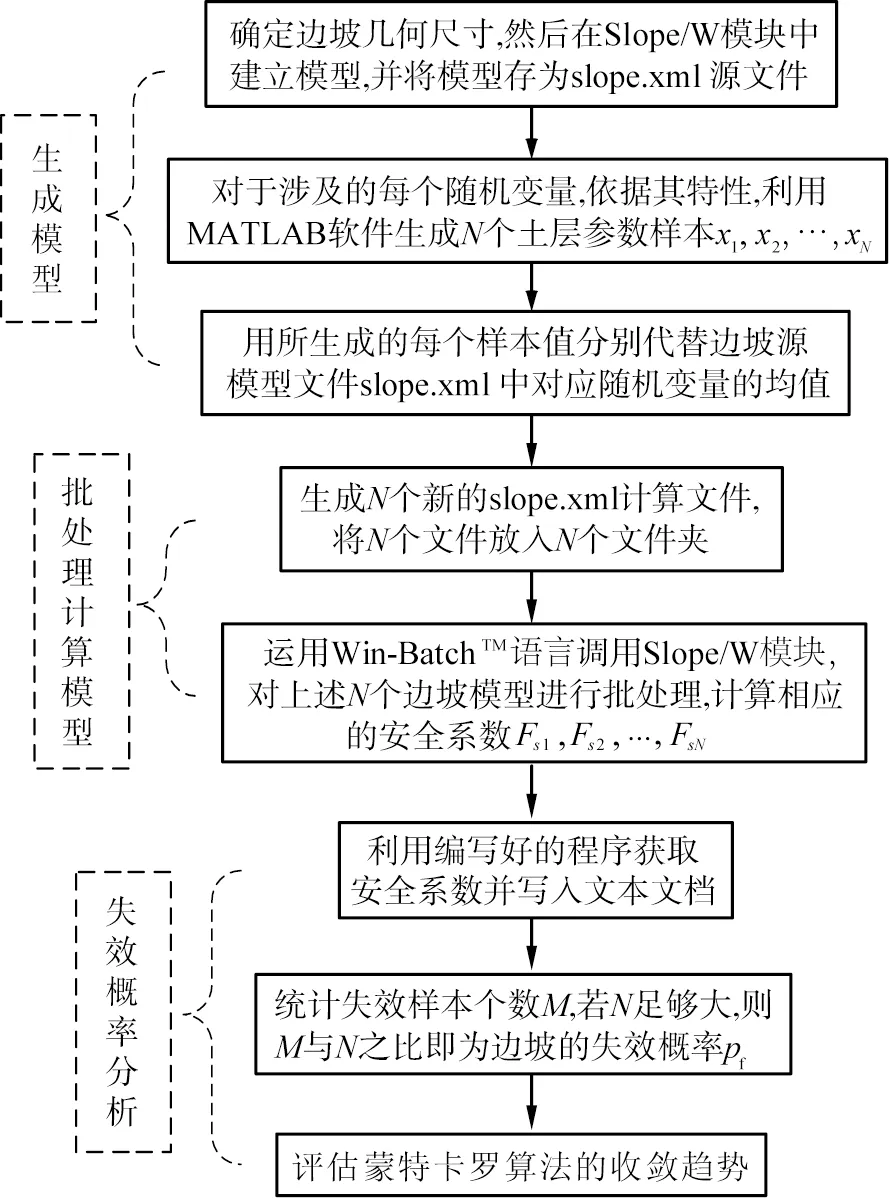
图1 基于Win-BatchTM语言的失效概率计算分析方法的计算流程

1)确定边坡几何尺寸，如坡高、 坡角、 土层分层，在Geo-Studio软件中的Slope/W模块中建立边坡稳定性分析模型，然后将边坡稳定性分析模型保存为slope.xml源文件。

2)依据土体基本变量的均值、标准差(或变异系数)，利用MATLAB软件生成N个土层参数样本x1,x2,…,xN。用所生成的每个样本值分别代替边坡源模型文件slope.xml中对应随机变量的均值，生成N个新的slope.xml计算文件，然后利用Fortran程序将该N个文件导入所建的N个文件夹。

3)基于极限平衡法，利用Win-BatchTM语言调用Slope/W模块，对N个土层参数样本进行批处理，计算相应的安全系数Fs1,Fs2,…,FsN。

4)利用Fortran程序提取计算的N个安全系数。

5)运用蒙特卡罗方法，统计失效样本个数M，若N足够大，则M与N之比即为边坡的失效概率pf。

6)根据不同样本个数时的失效概率，评估蒙特卡罗算法的收敛趋势。

1.4 某挡墙高度时加固边坡失效概率计算

在1.3节中得到的N个安全系数中， 对于安全系数小于1的样本， 可以利用光滑粒子流体动力学(smoothed particle hydrodynamics， SPH)方法分别模拟加高挡墙前、 后边坡失稳堆积状态， 如图2所示。由图可知：在未加高挡墙时，边坡失稳后有一定量的土粒滑至铁路线，给铁路运营带来不便；挡墙加高后，边坡失稳的土粒未越过挡墙滑至铁路线，因此原先的失效样本应重新定义为安全样本。与式(1)中基于安全系数的极限状态函数不同，重新定义基于边坡失稳堆积状态的极限状态函数为

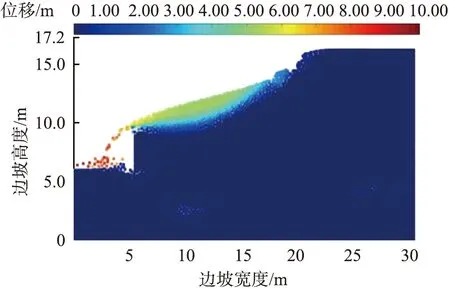
(a)加高前

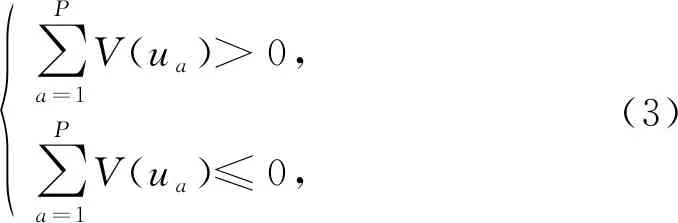
{∑Pa=1V(ua)>0,∑Pa=1V(ua)≤0,(3)

式中：P为土粒的个数总和；ua为第a个土粒；V为越过挡墙土粒的体积。

由式(3)可知，当越过挡墙土粒的个数总和小于或等于0时，该状态下的边坡是安全的，如果越过挡墙土粒的个数总和大于0时，该状态下的边坡是失效的。基于式(3)所示的极限状态函数，重新计算某挡墙高度时加固边坡失效概率，基本思路如下：在1.3节中得到的N个安全系数中，选择安全系数小于1的m个样本，按照安全系数Fs1,Fs2,…,Fsm由大到小的次序进行降序排列，相应的m个样本记为Z1，Z2，…，Zm,针对某特定挡墙高度Hk(k=1,2,…,n；n为挡墙高度取值个数)，自Z1开始，分别计算样本为Zt时边坡失稳后的堆积状态，其中Zt为临界失效样本确定所需要的第t个变量(t=1,2,…,m)。并利用式(3)判断边坡是否失效，重复计算，直至计算得到第1个发生失效的样本，称为临界失效样本Zd(d=1,2,…,m)，确定临界失效样本的流程如图3所示。如果m个样本分析完成后，所有样本均未发生失效，则临界样本为安全系数最小的失效样本Zm。剔除Z1—Zd-1中未发生失效的样本，剩余发生失效的样本个数与样本总数N的比值即为某挡墙高度时加固边坡的失效概率pf=(m-d+1)/N。

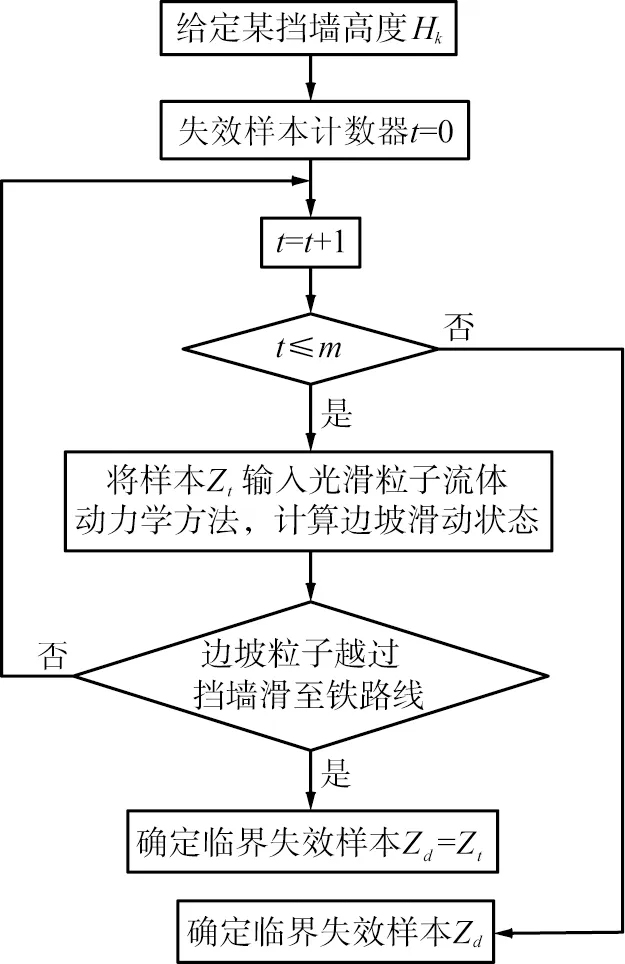
k=1,2,…,n，n为挡墙高度取值个数；t=1,2,…,m，m为安全系数小于1的样本个数；d=1,2,…,m。

给出一系列设定挡墙高度，记为H1，H2，…，Hn，采用上述方法，类似可以得到其他设定挡墙高度时的边坡的失效概率，分别记为pf1，pf2，…,pfn。根据设定的挡墙高度及其对应的边坡的失效概率绘制挡墙高度与边坡的失效概率关系曲线。

2 算例分析

2.1 工程概况

图4所示为哈佳铁路某段原始边坡，该原始边坡土层分别为粉质黏土、砂岩。滑坡后进行加固施工，清除左侧段溜坍部分，坡体沿底面挖台阶，台阶宽度为2.0 m。边坡坡面至原坡面或坍塌底面夯填粗颗粒土。本文中对该加固边坡进行可靠度分析，并对挡墙高度进行优化。

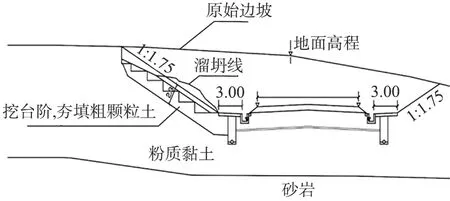
图4 哈佳铁路原始边坡

2.2 加固边坡确定性分析

为了评估加固边坡稳定程度，利用Geo-Studio软件中的Slope/W模块计算安全系数。 在建模前， 简化边坡，保留路堑边坡部分，保留路基左侧的挡土结构，简化掉路基路面部分， 哈佳铁路某段原始边坡简化后的边坡如图5所示， 边坡坡率为1∶1.75， 溜坍部分清理后回填粗颗粒土并夯实。 根据图5， 利用Geo-Studio软件建立边坡几何模型， 如图6所示。 根据地质勘测报告综合确定各土类参数， 如表1所示。

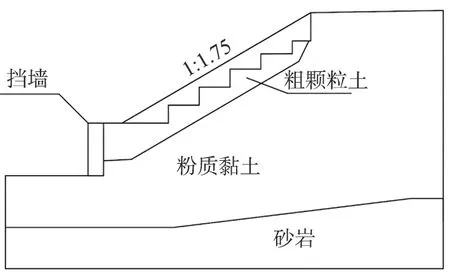
图5 哈佳铁路某段原始边坡简化后的边坡

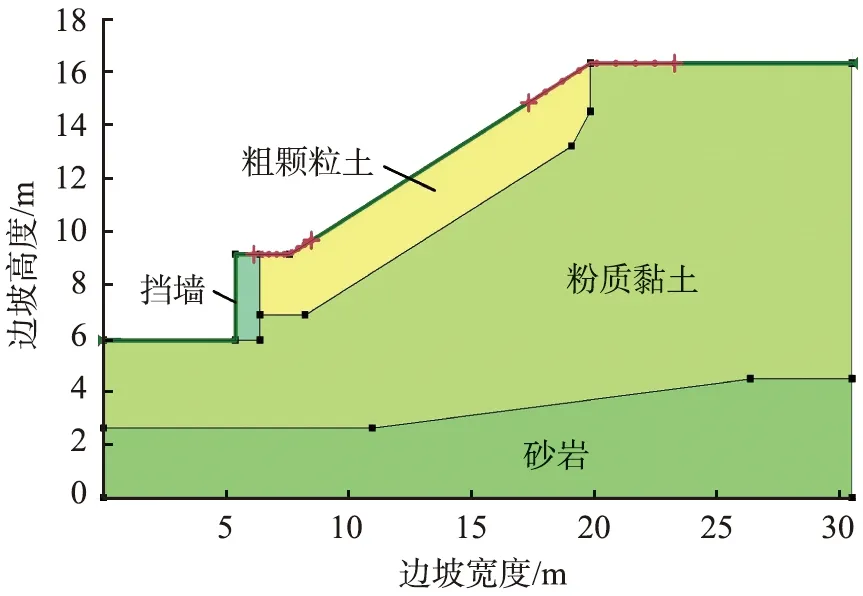
图6 利用Geo-Studio软件建立的边坡几何模型

将表1中各土类的黏聚力、 内摩擦角和容重的均值输入图6中的边坡几何模型中， 几何模型中挡墙材料利用基岩进行模拟。 计算得出安全系数为1.383， 并得到边坡几何模型相应的圆弧滑动面如图7所示。 因为安全系数大于1， 所以加固后的边坡是稳定的。

表1 根据地质勘测报告综合确定的各土类参数

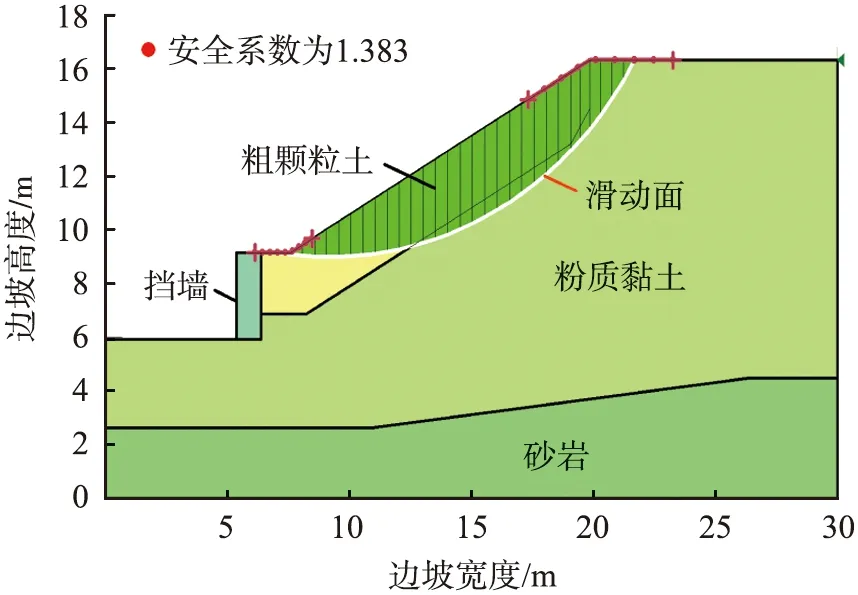
图7 边坡几何模型相应的圆弧滑动面

3 失效概率分析

3.1 总样本个数N对失效概率影响

由确定性分析方法可知，图7所示的加固边坡是稳定的。为了考虑夯填粗颗粒土和粉质黏土参数的不确定性，进行加固边坡的可靠度分析。将粗颗粒土内摩擦角、 粉质黏土黏聚力、 粉质黏土内摩擦角视为对数正态随机变量，统计参数见表1。假定随机变量独立分布，生成5 000个样本，样本值的频率如图8所示。基于极限平衡法，按照1.3节中批处理操作步骤，生成的安全系数直方图如图9所示，由图可知，安全系数服从非正态分布，其中红色样本为失效样本，蓝色样本为非失效样本。经统计可知，失效样本个数M=1 361，则边坡失效的概率为pf=136 1/5 000=27.2%。为了确保所用随机样本数量足够大，评估蒙特卡罗算法的收敛性，结果如图10所示。从图可知，当总样本数N较小时，计算所得pf波动明显。当N大于2 000后，pf基本不再变化。由此可知，本文中所用N=5 000已足够大。

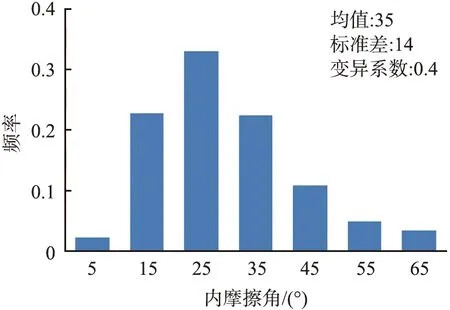
(a)粗颗粒土内摩擦角

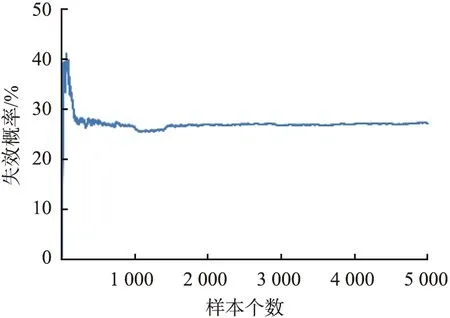
图10 蒙特卡罗算法收敛性评估结果

3.2 回填土夯实效果对失效概率的影响

考虑到施工因素的不确定性，夯填粗颗粒土的内摩擦角变异性受施工因素影响较大。改变表1中粗颗粒土内摩擦角的变异系数为0.3、 0.2， 利用1.4、 3.1节中的方法， 得到不同变异系数时的加固边坡失效概率， 如表2所示。 由表可知， 随着粗颗粒土内摩擦角变异系数增大， 边坡失效概率增大， 因此， 在施工过程中， 加强施工质量监督是非常重要的。

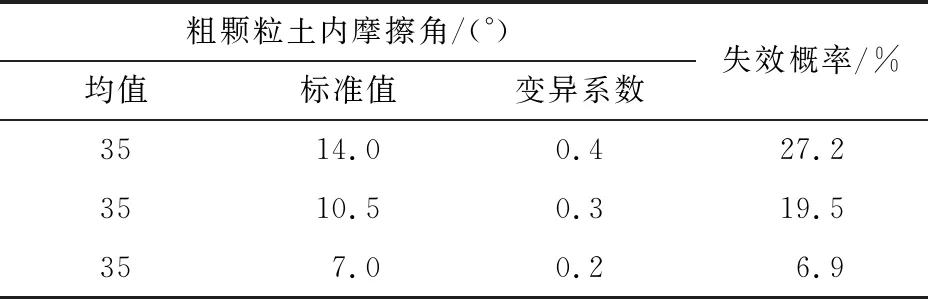
表2 不同变异系数时的失效概率

3.3 挡墙高度对失效概率影响

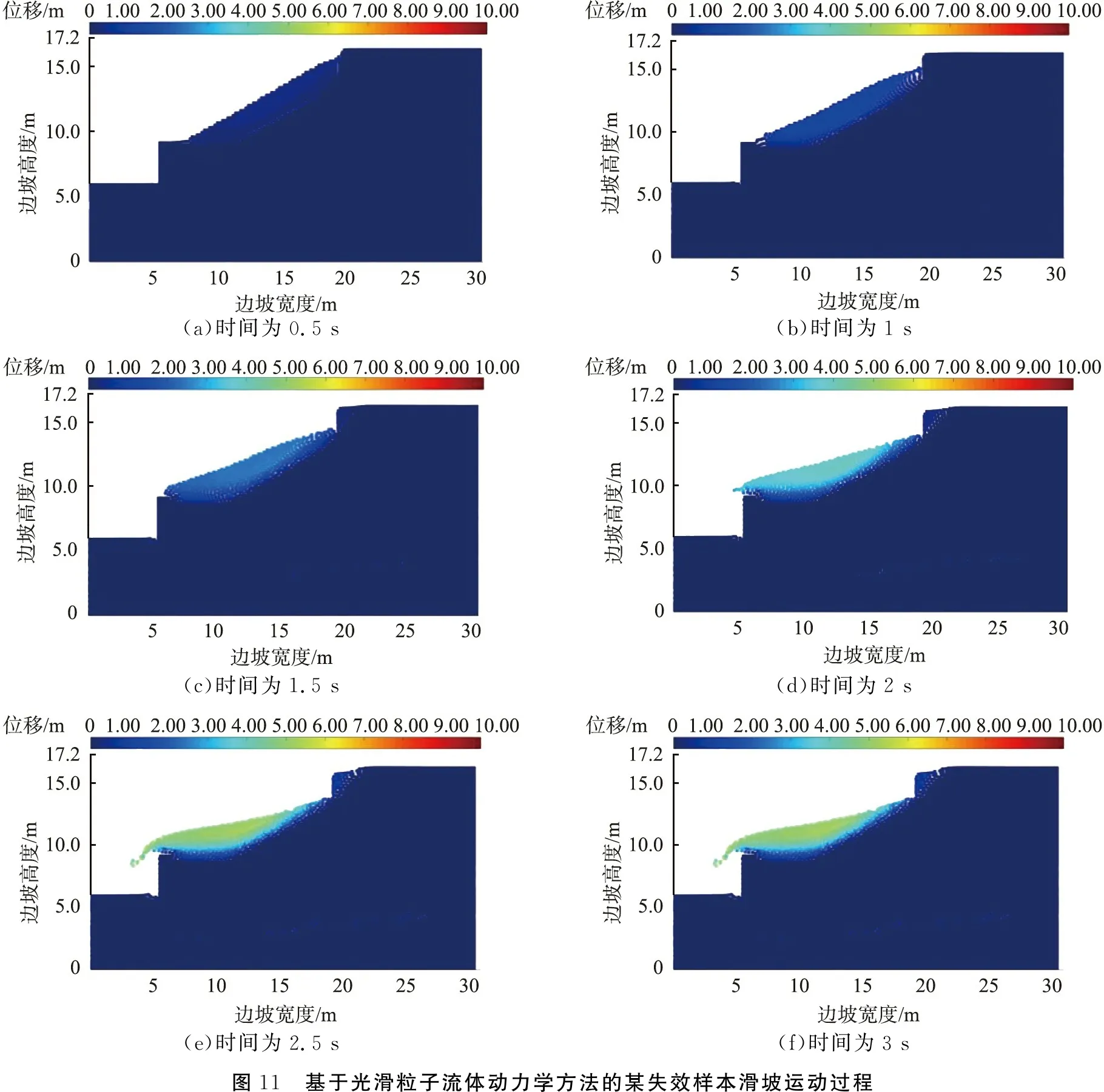
当滑坡发生后，滑动土体运动至铁路线，阻挡铁路正常运营。利用SPH方法对某失效样本进行滑坡整个运动过程模拟， 如图11所示。 由图可知， 从开始发生滑动时计时， 当滑动时间为0.5 s时，坡顶出现裂缝， 当滑动时间为1 s时，坡脚土体开始隆起，夯填土体整体开始下滑，至滑动时间为3 s时，部分粗颗粒土滑落至铁路线，产生不利后果。

为了分析挡墙高度增加后对边坡失效概率的影响， 从样本中抽取部分安全系数小于1的样本， 得到3个安全系数分别为0.687、 0.718、 0.751的边坡模型样本。将这3个边坡模型样本的挡墙高度增加1 m，然后利用SPH方法进行模拟，结果如图12所示。

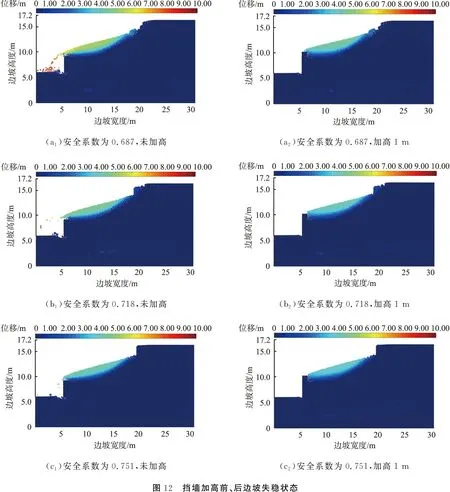
当夯填土变异系数为0.4时，给出一系列设定挡墙高度H1=0 m，H2=0.2 m，H3=0.4 m，H4=0.6 m，H5=0.8 m，H6=1.0 m。针对某挡墙高度Hk(k=1,2,…,6)，利用图3所示的流程，确定临界样本Zd，进而剔除样本Z1—Zd-1，得出不同挡墙高度时发生失效样本的个数，如图13所示。为了研究不同夯填土变异系数时挡墙加高对边坡失效概率的影响，利用1.4节中的方法计算得到不同挡墙高度时加固边坡的失效概率，结果见表3。夯填土不同变异系数时加固边坡失效概率与加高挡墙高度变化如图14所示。从图中可以看出，当夯填土参数变异系数为0.4时，在挡墙逐渐加高的情况下，加固边坡失效概率从27.2%降至2.58%，表明增加挡墙高度可以有效降低加固边坡失效概率。在变异系数小于0.4的条件下，挡墙高度增加1 m时边坡失效概率的降低程度更明显。

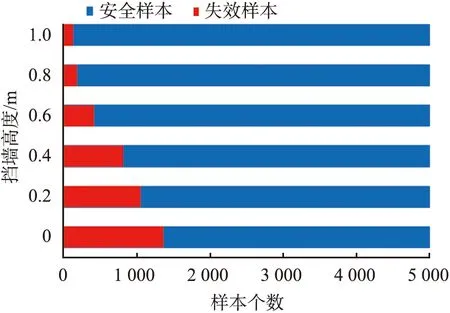
图13 变异系数为0.4的条件下设定挡墙高度不同时的失效样本个数

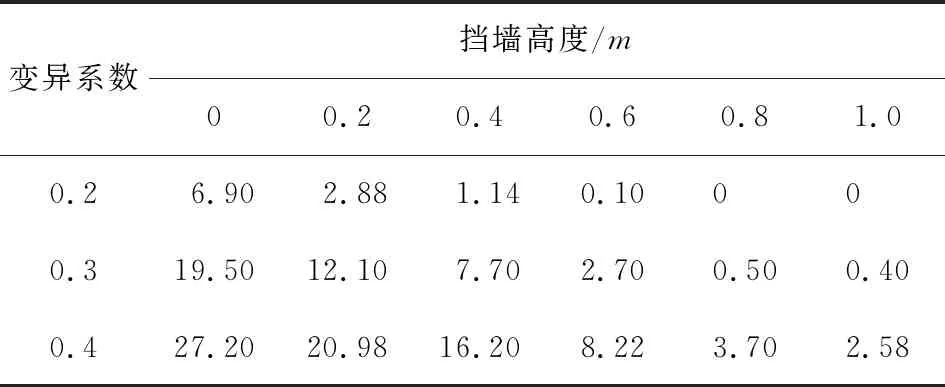
表3 夯填土变异系数不同时加固边坡增加设定挡墙高度后的失效概率 %

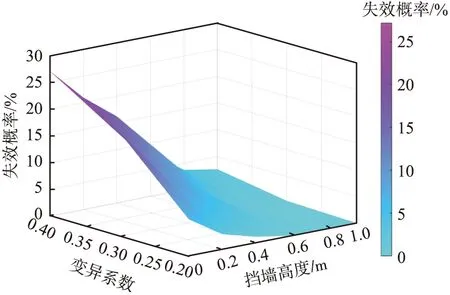
图14 夯填土变异系数不同时加固边坡失效概率与加高挡墙高度变化

4 结语

本文中基于加固边坡进行了挡土墙高度的优化，结合SPH方法研究了挡墙高度对加固边坡失效概率的影响。通过工程实例验证了增加挡墙高度可以很大程度地降低边坡的失效概率。研究结果表明，在实际工程中严格控制施工质量以降低夯填土参数的变异性，可以有效降低加固边坡的失效概率。在工程中可参考夯填土不同变异系数时加固边坡失效概率与加高挡墙高度变化的三维图，对挡墙高度进行设计施工，从而方便施工人员对加固边坡挡墙高度进行优化。

在实际工程中，滑坡滑动后，运动的土体在下滑时速度增加，挡墙是否能够抵挡土体对挡墙的冲击并能保持稳定的问题仍需要进一步探究。