引导学生积极思考解决数学问题的策略

云南省普洱市第一中学 徐文辉

一、多方面素质教育

素质教育是多方面的，但培养学生的数学思维品质的主战场在课堂。教学效果如何，直接影响学生素质的发展、提高。随着课程改革的进一步深入，数学教师更需要发挥自身的主导作用，通过学生的思考、合作探究，体现学生在学习中的主体地位。教师应通过教育教学活动，使学生的素质结构发生变化。不论教学过程如何改革，教师在整个教学活动中一定要起主导作用。学生的自主学习、合作探究既能使学生个性充分发展，又能使学生整体素质全面改善和提高。数学教学的最终目的，不仅在于传授数学知识，还在于通过课堂师生互动，提高学生的思维品质和能力。

二、引导学生积极思维

教师在教学活动中，引导学生积极思维、积极参与教育教学活动，成为数学教学的基本任务。教师不仅仅是传授知识，告诉学生什么知识点重要，学生只是记住知识，思考不够，没有创造性。整堂课的教学氛围比较死板，这种不适应现代教学模式与教学的氛围都是极为不好的。当今社会，教育需要为国家培养更多有创造性的、高质量的人才，作为数学教师更需要在数学课堂中提高教学质量。教师要在课堂中通过引导学生积极思考，提高其解决数学问题的能力。教师把课堂需要讲授的知识变得更加具体与形象，从而方便学生对于这些知识点的理解。下面笔者就一节三角函数复习课的教学，通过问题导引的方法，让学生自己思考逐渐得出结论。

课前检测：求值：（1）sin585°；（2）cos600°；（3）sin15°；（4）sin7.5°。

这几个题都较为简单，学生容易得出正确结论。

例1：求sin18°的值。分析：此题学生不容易想到解法，但有了课前检测的四个题以后，我们可以避虚求实，先总结前面四个题的解题规律：都转化为了特殊角求解。教师就可以引导提问：能否把18°也转化为特殊角？学生通过思考容易得出5×18°=90°，但不一定就能求sin18°的值，通过教师进一步引导可以得出：显然5×18°=90°不容易计算，可以变为2×18°=90°-3×18°，两边取正弦。教师还可以继续引导学生：为了书写方便，不妨设α=18°，变为：2ɑ=90°-3ɑ，进而问题变成了求Sinɑ。

教师通过层层设问，加以小组讨论，逐渐引导学生得出正确的解法如下。

经过不断的尝试、思考，学生得到了此题的简便解法如下。

例3：求cos2A+cos2（60°-A）+cos2（60°+A）的值。

分析：三角求值问题的解决，我们首先要熟悉三角公式，找到思路后才能正确地解决问题。此题已知式为三角平方式，较难求解，通过分析、思考，学生容易想到用降幂公式把它降次，再化简进行求解，得到解法如下。

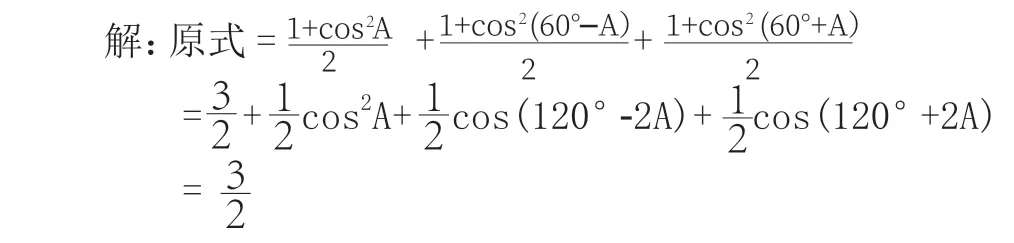
已知式为三角平方式，较难求解，学生通过降幂的方法找到了一种较为简洁的解法。在此基础上，教师还想让学生进一步探讨：还有没有其他解题思路？请同学们考虑一下可不可以增加从平方式出发，直接求解。（点拨）

学生通过思考、议论，还是没有思路。这时，教师可以进一步引导学生得出：原式都是角的余弦的平方，则角的余弦的平方与同角的正弦的平方和为1，角的余弦的平方与同角的正弦的平方差为二倍角的余弦。

问题是题目中只有角的余弦的平方，既然角的余弦与正弦的平方和与平方差都能达到化简式子的目的，那么我们不妨构造一个与之对应的正弦式，一起进行考虑。

显然，虽然这种方法的思路让我们有了一种茅塞顿开的感觉，但是不容易想到，这就需要同学们通过学习不断积淀，不断认识理解。此种方法我们把它称之为构造对偶式解题，值得同学们借鉴。

通过教师的层层点拨，学生在这个过程中一直在思考，既拓展了解题思路，又锻炼了思维。

思考题：（1）（1995 年高考理科）求sin220°+cos250°+sin20°cos50°的值。

（2）化简：sin2ɑ+sin2β+2sinɑsinβcos(α+β)。

提示：第（1）题同学们考虑用基本方法解决，需要用到课本中的和差化积与积化和差公式。

问题：如果第（2）题化简得到的结论，可以用来解决第（1）题吗？

总之，一节课好与不好，怎么上，关键是教师主导地位、学生主体地位的充分体现。采用问题导引的方式进行教学，关键是教师提出问题，真正能够让学生进行探索，得出结论。要让学生自主探索，就必须让学生想动、能动、有兴趣动。因此，教师的设问方式就非常重要，笔者认为还需要注意以下几方面：第一是目的性，即使学生钻研所设置的问题是有目的的、必要的；第二是可行性，即所设置的问题的难易程度必须适合学生的能力水平，问题过难，会使学生劳而无功或望而生畏，问题过于简单，则失去了意义；第三是刺激性，让学生有“奇”，能起到激发学生思维、积极探索提高兴趣的作用。

做一道题应该有一道题的收获。有几种解法、基本解法能得出什么结论、可否推广，都是我们做题应该思考的问题。此节课的教学，体现了教师的主导作用、学生的主体地位，整节课，教师始终是一个引导者，学生始终处于思考、训练、动脑、动手之中，调动了学生思考的积极性，既使学生思维得到了锻炼，又使学生通过逐渐学习，学会思考，体现了数学教学的目的不仅仅是传授知识，更重要的是学会思考，从而培养学生的核心素养。