重载轮式移动机器人路径跟踪滑模预测控制

陈 勇，刘 哲，乔 健，卢清华

(佛山科学技术学院 机电工程与自动化学院，广东 佛山 528225)

1 引言

重载移动机器人在动态建模[1]、导航技术[2]、能耗计算[3]、运动控制[4]等领域的研究深受国内外学者关注。与普通轮式移动机器人不同，重载移动机器人具有较大承载能力的特点，使得其在变压器、铝型材等重物运输过程中具有广泛的应用前景。

重载移动机器人结构特点导致的路径跟踪速度和稳定性问题相比于一般轮式机器人显得更为复杂[5]，预测控制用于移动机器人的运动过程调节，能够提升计算速度，加快移动机器人轨迹跟踪的速度，已经应用到移动机器人控制的各个领域[6]。文献[7]提出了一种预测控制器来控制两轮式移动机器人轨迹跟踪，采用饱和技术优化最大和最小控制值，简化控制器算法。文献[8]将重型车辆的行驶任务描述为一个最优控制问题，通过模型预测控制器实现能耗节省。文献[9]提出了一种模型预测控制基于WMR轨迹规划的控制算法，解决了其他控制算法只能处理部分机器人约束点的问题。文献[10]提出了一种基于神经网络优化的鲁棒模型预测控制方法来稳定具有物理约束的移动机器人，通过神经网络算法增加模型预测控制的稳定性。文献[11]提出了一种基于量子粒子群优化的模型预测控制方法，用以解决机器人速度跳变和速度跳变引起的驱动饱和问题。

作为一种结构简单的新型控制方法，滑模控制在移动机器人的运动控制中得到了广泛应用。文献[12]针对欠驱动两轮移动机器人，提出了一种引入线性控制器的新积分滑模控制器。文献[13]针对移动机器人的参数不确定性，设计了基于神经网络的模型预测控制器，实现轨迹跟踪控制。文献[14]应用动态环境下谐波势场的在线修正，提出了一种多级滑模控制器移动机器人的动态避障策略，使机器人在非已知轨迹上以时变速度运动时避免与障碍物的碰撞。文献[15]设计了基于指数趋近律的滑模控制方法，保证在大阶跃情况下系统仍然能以较大的速度趋近于滑动模态。文献[16]针对移动机器人的路径跟踪控制问题，提出了一种全局稳定定理与指数趋近律相结合的滑模控制方法，采用双环闭环控制结构提高了机器人在路径跟踪过程中的线速度与角速度的稳定性，削弱了指数控制律的抖振现象。

本文首先分析了重载移动机器人运动学与动力学特性，建立了重载轮式移动机器人运动学与动力学模型，基于动力学模型设计了预测控制器，并加入位置滑模控制，结合滑模控制和预测控制的优点，提出了基于动力学的滑模预测控制方法，提高了路径跟踪速度和稳定性。

2 重载轮式移动机器人运动学建模

如式(1)所示，在不考虑摩擦力、向心力、侧滑等外部扰动因素下，可以建立轮式移动机器人的运动学方程。

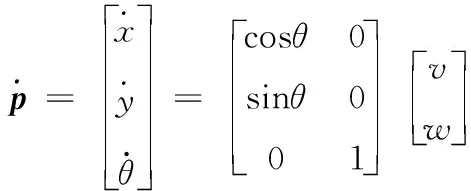
(1)

3 重载轮式移动机器人动力学建模

应用于物流运输中的移动机器人载重量通常为几十公斤甚至超过1 000 kg，本文重载移动机器人最大载荷量可达8 000 kg，其关键技术问题为重载移动机器人舵轮的控制，单轮承重可达2 t，使用4个同样载荷量的轮子，针对其中两个舵轮进行控制。

系统进行转向时，左后轮不产生偏转角，需要分析右前方驱动轮的纵向力和侧向力，考虑到四轮式结构的绕z轴转动惯量分析复杂，垂直于轴心的力大小不能用准确的力学分析得到，简化模型假设后方两个轮子都没有偏转角，并且分析轴心转动动力学时近似成单轨模型，如图1所示。

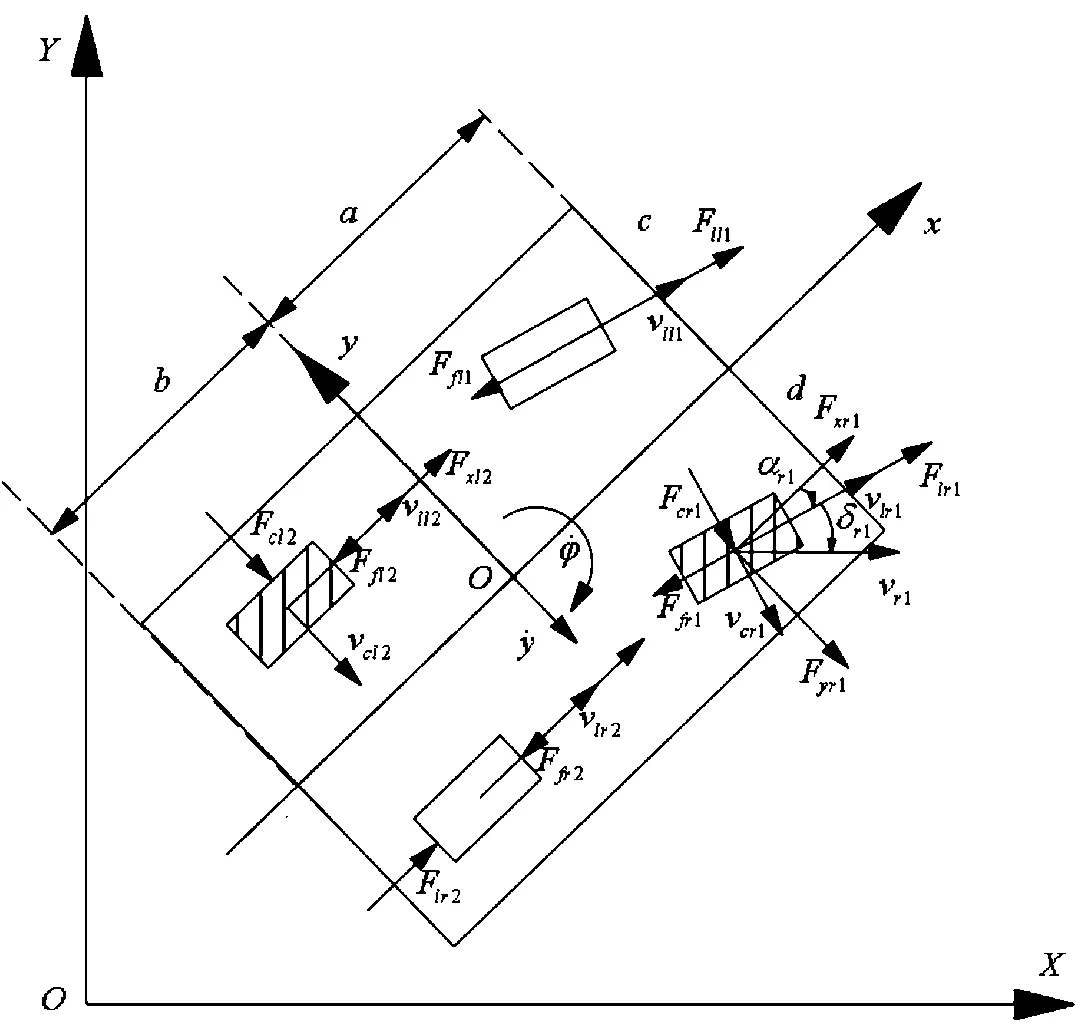
图1 轮式移动机器人动力学模型示意图

在x轴方向上有：

在y轴方向上有：

则z轴的方向上的动力学方程为

通过侧向力和纵向力列出驱动轮在x轴、y轴方向受到的合力：

移动机器人进行转向运动时，轮子受到的纵向力和侧向摩擦力与轮子的偏转角α、滑移率s、纵向负载Mg+F、轮子与路面的摩擦系数μ等参数构成如下函数关系：

其一般方法由以下公式给出：

式中，x=s+Sh,S是纵向滑移率，Sh和Sν分别代表曲线水平方向漂移和纵向水平方向漂移。C为曲线外形系数,D为曲线最大值系数,B为刚度系数，E为曲率系数。

由于速度与位置的约束，轮子的偏转角α可以由三角函数算出：

αr1=tan-1(vcr1/vlr1)

轮子速度为

滑移率s可由经验公式计算：

驱动轮所受垂向载荷可由下面公式计算：

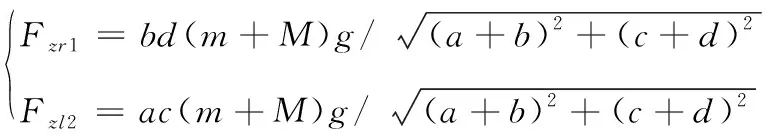
机器人转向运动时的动力学模型为：

由上述分析得知，纵向力和侧向力的函数关系中，只有驱动轮偏转角α为未知，在实际的机器人运动控制中，可以测得偏转角的动态变化，因此可以把偏转角作为控制变量当作系统的输入，得系统的动力学方程的空间状态方程如式(2)所示。

(2)

4 预测控制设计

4.1 动力学方程线性化与离散化

采用泰勒公式法对非线性系统进行线性化。首先要保证系统在该时刻有n阶导数，并且在该时刻的开区间上n+1阶可导。针对式(2)所示的动力学的空间状态方程，使用泰勒级数展开，只保留泰勒级数的一阶项，则有：

上式可写成：

u=γ(ηt,ut)+Jγ(η)(η-ηt)+Jγ(u)(u-ut)

式中Jγ(x)为泰勒展开式的近似雅可比矩阵。

误差线性化得到：

模型预测控制是针对状态方程采用模型预测控制算法，建立步长，并根据其当前状态计算下一步的动作，需要状态方程是离散化的，采用欧拉法对线性方程进行离散处理。

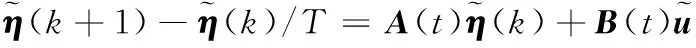
状态空间表达式如式(3)所示。

(3)

其中：A1=I+TA(t)，B1=TB(t)

4.2 滑模预测控制器

针对如下离散化状态方程：

定义线性误差方程：

E=ηk+T-ηk

其中：ηk+T为η的在k+T时刻的参考值。

(4)

利用全局稳定指数趋近律设计滑模切换函数，如式(5)所示。

(5)

为使系统尽可能地达到每一时刻的参考值，有：

min{(ηk+T-ηk)TQ(ηk+T-ηk)+(uk+T-uk)TR(uk+T-uk)}

其中：Q为权重因子。对一般二次型规划问题有以下形式：

对于时间步长的周期内得到求解后，可以得到控制时域内的控制量和控制变化量如式(6)和式(7)所示。

U=[u(k),u(k+1),u(k+2),…]T

(6)

ΔU=u(k+T)-u(k)

(7)

将u(k)作为实际的输入用于系统，在下个周期更新，以此类推，完成系统预测跟踪控制。

4.3 控制器约束条件

在实际的移动机器人动力学运动控制中，其环境通常是复杂的，为适应场合的多样性，需要对机器人建立约束条件，如式(8)～式(10)所示。

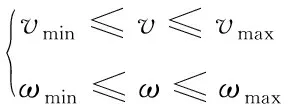
(8)

(9)

(10)

式(8)为速度和角速度约束；式(9)为加速度与角加速度约束；式(10)为位置约束与姿态角约束。

5 仿真实验与验证

对四轮式对角双驱动移动机器人动力学滑模预测控制进行CarSim和Matlab联合仿真，通过动力学模型建立，控制移动机器人后轮和前轮作为驱动轮，分析移动机器人在固定速度、不同速度、滑模预测控制与预测控制对比、障碍干扰等情况下的移动机器人位置、姿态角、前驱动轮偏转角的跟踪情况。

滑模预测流程如图2所示。移动机器人4个轮子采用四角对称放置，左右间距为2 m，前轮与后轮到质心距离均为3.5 m，车体及荷载总质量为7 000 kg，仿真路径为经典双移线(DLC)轨迹。

图2 滑模预测控制流程框图

5.1 固定速度下双移线路径跟踪仿真

选择移动机器人速度为1 m/s，路径为双移线运动轨迹，路径跟踪运动时间为15 s，移动机器人的路径跟踪过程中的位置、姿态角、驱动轮偏转角如图3～图5所示。

图3中实线部分为预设路径，虚线部分为速度是1 m/s时沿预设路径的跟踪路径，机器人路径基本可以跟踪预设路径。图4为路径跟踪时机器人的姿态角变化，能够吻合双移线中的姿态角。图5为机器人运动时转向驱动轮的偏转角，其控制移动机器人的转向，移动机器人姿态角的变化随机器人转向轮偏转角的变化而变化。

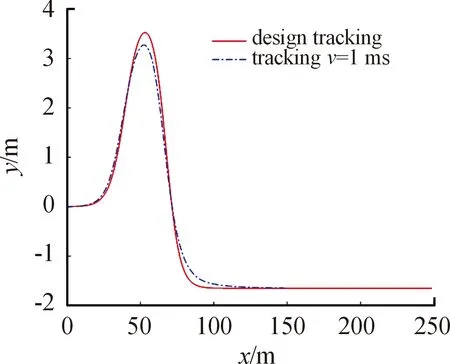
图3 固定速度下移动过程中机器人位置曲线

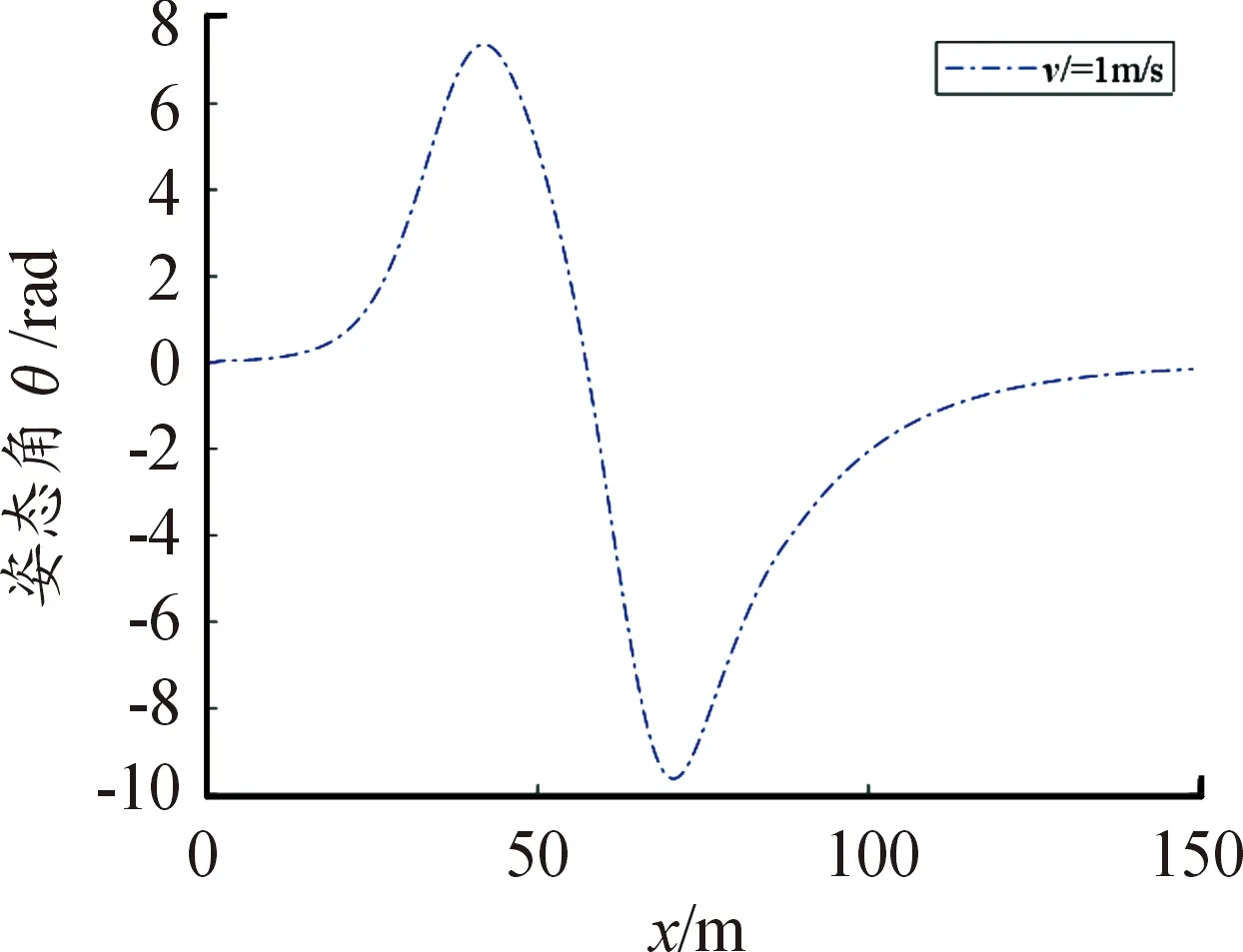
图4 固定速度下移动过程中机器人姿态角曲线

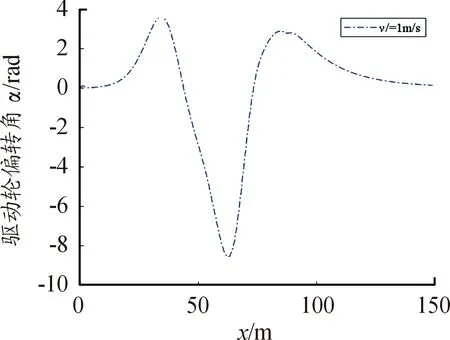
图5 固定速度下移动过程中驱动轮偏转角曲线

5.2 不同速度下双移线路径跟踪仿真

取移动机器人速度与运动时间条件分别为：1)速度为0.5 m/s、仿真时间25 s；2)速度为0.75 m/s、仿真时间20 s；3)速度为1 m/s、仿真时间15 s。

移动机器人在不同移动速度时的路径跟踪过程中的位置、姿态角、右前轮偏转角如图6～图8所示，分别为移动机器人速度为重载移动机器人速度分别为0.5 m/s、1 m/s和0.75 m/s时路径跟踪状态。

图6 不同速度下移动过程中机器人位置曲线

图7 不同速度下移动过程中机器人姿态角曲线

图8 不同速度下移动过程中机器人驱动轮偏转角曲线

从机器人3种不同速度的响应可以看出，机器人的速度改变对其路径和姿态角的有一定的影响，机器人速度越大，路径跟踪过程越快，在转角路径时的偏差就越小，能够快速地完成转向。

5.3 固定速度下滑模预测控制与预测控制对比试验

取移动机器人速度为1 m/s，仿真时间为15 s，预测步长为0.3 s，控制步长为0.075 s，观察对移动机器人分别在滑模预测控制(SDMPC)和预测控制(MPC)下的轨迹变化、姿态角变化和偏转角变化，如图9～图11所示。

图9 移动过程中机器人位置曲线Fig.9 Comparison of robot position in moving process

从图9～图11可以看出：滑模预测控制(SDMPC)和预测控制(MPC)的对比仿真实验中，二者路径和姿态角变化并无明显差别，但二者的驱动轮偏转角的对比中，在路径转弯处和运行到80 m后，预测控制明显存在较大的扰动现象，而滑模预测控制下的驱动轮偏转角更加稳定且无抖震现象，具有更好的跟踪性能。

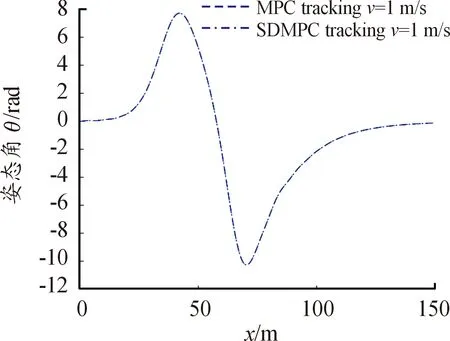
图10 移动过程中机器人姿态角曲线

图11 移动过程中机器人驱动轮偏转角变化曲线

5.4 扰动状态下的路径跟踪

取移动机器人速度为1 m/s，仿真时间为15 s，对移动机器人进行路径存在扰动情况下动力学滑模预测控制器的双移线轨迹路径，其运动路径、驱动轮偏转角变化如图12～图14所示，表明扰动状态下滑模预测控制器能保持有效性。

图12显示：移动机器人在运动过程中设计一处路径障碍(X轴76 m处)，移动机器人的控制器可以很好并及时地做出避障处理。图13为存在障碍路径中的姿态角变化，图14为路径跟踪时控制输入的转向驱动轮偏转角。

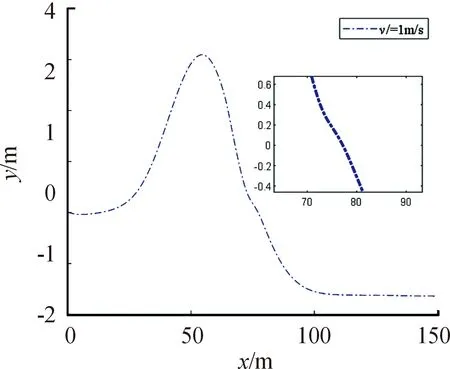
图12 存在扰动时的路径曲线

图13 存在扰动时的机器人姿态角曲线

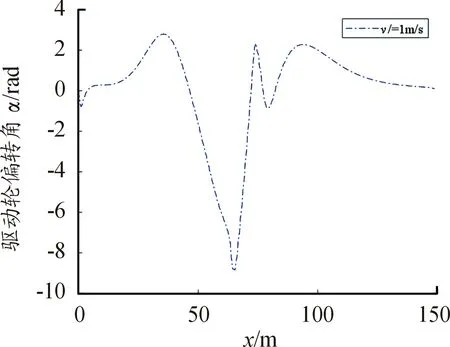
图14 存在扰动时的驱动轮偏转角曲线

6 结论

根据重载移动机器人结构，建立重载移动机器人的运动学模型和动力学建模。通过CarSim和Matlab联合仿真进行运动控制验证，分别分析了固定速度、不同速度、固定速度下滑模预测控制与预测控制及扰动干扰等情况下的移动机器人路径跟踪情况。仿真实验结果表明，滑模预测控制应用于机器人的路径控制过程，能较好地进行路径跟踪并进行有效避障，验证了相同路径下控制器的有效性。本文设计的控制器可以作为设计真实重载移动机器人控制系统的有效参考。