多等级区域侦察弹性星座设计方法
2021-09-03王浩张占月张海涛姜平
王浩,张占月,张海涛,姜平
1. 航天工程大学,北京 101400 2. 中国人民解放军63601部队,酒泉 732750
1 引言
传统侦察星座单星体积大、集成度高、造成了星座成本高、弹性低的缺陷[1]。以小卫星为主体的侦察星座应用模式降低了星座成本,同时使得弹性星座建设成为可能。星座设计过程多将区域内所有目标视为同等重要,而在实际任务中区域内不同目标的重要程度一般不同,需对区域内目标按重要程度的不同进行分级,考虑等级信息后对星座进行设计。提出多等级区域侦察弹性星座,并对其设计方法进行研究,其中多等级是指将目标区域按照重要程度不同分为多个子区域,弹性是指星座因故受损后其性能依然在可接受范围之内。
目前国内外对星座设计方法的研究多集中于三个方面,一是针对特定构型的星座设计方法,如常见的Walker星座、Flower星座,该类型星座构型相对固定,卫星间排列存在一定规律,只需对关键参数进行确定,星座构型即可确定。如文献[2]提出了一种低轨导航星座的设计方法,通过组合不同的Walker星座,在全球覆盖要求的基础上实现对不同纬度地区可见星数量和DOP值的均匀分布。文献[3]对Flower星座进行研究,选择全球均匀分布的3000点的最大GDOP值作为优化目标,通过优化算法对卫星数量在18~40颗的Flower星座最优构型求解,结果表明任何少于23颗卫星的Flower星座均无法满足基础的全球定位需求。二是基于解析或半解析的非特定构型星座设计方法,文献[4]基于回归轨道特性推导了卫星数与轨道面和最小重访时间之间的关系,提出了一种解析计算星座卫星数及轨道面数的高效方法。文献[5]提出一种通过几何关系计算星座对地间断覆盖的方法,并将此种方法运用于区域间断覆盖星座设计中。文献[6]对共地面轨迹回归星座设计方法进行研究,构建了共地面轨迹回归星座优化模型,将基准卫星的可见时间和星座构型向量近似为离散信号,提出一种循环卷积的方法用于计算星座覆盖性能,可用于多目标多星座的耦合优化;三是基于群智能优化方法的星座设计方法。目前应用于星座设计的群智能优化算法有NSGA-II[7],ε-Multiobjective Evolutionary Algorithm[8](ε-MOEA)、Particle Swarm Optim-ization[9](PSO)、Simulated Annealing[10]等,文献[9]对PSO算法进行改进,重新设置了粒子交换规则,增强了算法全局搜索能力,并应用于高分辨率遥感星座设计中。文献[11]对Genetic Algorithm(GA)、Differential Evolution Algorithm(DE)、Immmune Algorithm(IA)及PSO算法在星座优化问题中的性能进行了比较,结果表明DE算法具有较强的全局搜索和局部搜索能力。
传统区域侦察星座设计时重点关注于覆盖性能与成本之间关系的权衡,忽略了弹性对星座构型的影响,导致星座弹性弱,抗毁性差。大多设计方法采用相同的轨道高度和倾角的星座构型,导致星座对区域任意点的覆盖能力无法区分。针对上述问题,本文提出多等级区域侦察弹性星座设计方法,按照区域信息将星座设计过程分为多个子星座逐步设计,不同子星座轨道高度和倾角存在差异,实现了对区域覆盖和弹性分级的设计要求。考虑升交点漂移同步约束对星座设计,解决了混合构型星座构型稳定性问题。考虑星座弹性指标进行设计,增强了星座的弹性。
2 设计指标选取及设计需求描述
2.1 设计指标选取
本文选取最大重访时间和空间分辨率作为星座覆盖能力的度量指标[13]。最大重访时间的计算方法可采用常规的网格点法计算,空间分辨率可根据不同类型载荷的分辨率计算公式得到。选用Small Satellite Cost Model(SSCM)[14]模型对星座成本进行估计。
除了考虑覆盖和成本外,弹性在小卫星星座设计中也是必须考虑的性能指标。弹性可通过星座受损后覆盖能力下降程度来衡量,本文更关注最大重访时间的下降程度。定义弹性指数为星座受损状态最大重访时间下降幅度相对于满站位状态下最大重访时间的比例[15],弹性指数G如式(1)所示,定义受损状态为星座内任意1颗卫星失效导致最大重访时间下降最大所对应的状态。
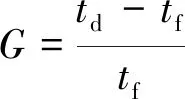
(1)
式中,tf为星座满站位状态下的最大重访时间,td为星座受损状态下(1颗卫星失效)的最大重访时间。
2.2 设计需求描述
对多等级区域侦察弹性星座设计需求进行描述。以区域被划分为3个等级为例,将目标区域按照重要程度由高到低划分为Ⅰ类区域、Ⅱ类区域和Ⅲ类区域。考虑最大重访时间、地面最低分辨率、星座成本及弹性指数等设计指标进行设计,要求设计星座对不同等级子区域的最大重访时间及地面最低分辨率不同,Ⅰ类区域最优,Ⅱ类区域次之,Ⅲ类区域最低;要求星座对Ⅰ类区域的弹性指数最优,对Ⅱ类区域的弹性指数次之,Ⅲ类区域重要程度较低,故设计过程不考虑Ⅲ类区域的弹性指数。
3 组网设计步骤
由于3类区域各设计指标存在分级,难以一次性设计出满足所有要求的星座,所以将星座设计过程按照区域等级信息分为多个子星座逐步设计,子星座内轨道高度、倾角和面内卫星数均相同,不同子星座间轨道高度、倾角和面内卫星数不同。设计流程如图1所示,步骤如下:

图1 星座设计流程Fig.1 Constellation design process
1)首先设计一类基础星座用于满足整个区域的最低覆盖要求,即Ⅲ类区域的覆盖要求。
2)计算基础星座对Ⅱ类区域的覆盖指标和弹性指标,若满足Ⅱ类区域的覆盖和弹性要求,则进行第4步,若不满足,则进行第3步。
3)在基础星座上设计一类子星座1,用于提升星座对Ⅱ类区域的覆盖和弹性能力,使其分别满足Ⅱ类区域设计要求。
4)计算基础星座和子星座1组成的混合星座对Ⅰ类区域的覆盖指标和弹性指标,若满足Ⅰ类区域的覆盖和弹性要求,则输出目标星座,目标星座即为基础星座和子星座1组合而成的星座。若不满足,则进行第5步。
5)在混合星座的基础上设计一类子星座2,用于提升星座对Ⅰ类区域的覆盖能力和弹性能力,使其满足Ⅰ类区域设计要求。目标星座为基础星座、子星座1和子星座2组合而成的星座。
4 组网设计模型与方法
考虑到小卫星体积小、结构简单的特点,一颗小卫星装配一种载荷,同种载荷设备参数一致。选用可见光载荷和SAR载荷搭配使用为目标区域提供高频率的探测。
4.1 组网参数计算
考虑到成像侦察小卫星载荷不具备大幅度的变焦能力,为保证拍摄稳定、图片清晰,选择近圆轨道作为成像侦察小卫星的工作轨道。假定星座内SAR卫星和可见光卫星参数均一致,采用可见光侦察卫星和SAR卫星混合搭配对区域进行侦察,保证星座对各类区域较高的分辨率同时能够弥补可见光卫星的工作条件限制。
(1)卫星轨道高度计算
根据可见光卫星对地最低分辨率可计算出满足此地面最低分辨率下的卫星轨道高度。卫星轨道高度选择范围为300~1 000 km[16]。可见光载荷为CCD相机,像元大小为p,焦距为f。如图2所示,当卫星垂直对地成像时,地面分辨率为Gnadir,如式(2)所示。

图2 可见光侦察卫星地面最低分辨率Fig.2 Lowest ground resolution of visible light reconnaissance satellite

(2)
式中:h为轨道高度。
当卫星侧摆α成像时,由图2中几何关系可计算地面最低分辨率为Goff,如式(3)所示。

(3)
式中:β为载荷视场半角;γ为卫星覆盖半角;Re为地球半径,取6 378.16 km。
由覆盖几何关系可得,卫星覆盖半角γ与轨道高度h之间满足式(4)[16]。
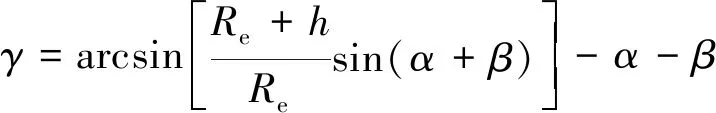
(4)
联立式(3)和式(4),可推导出轨道高度与地面最低分辨率之间的关系,如式(5)所示,当区域地面最低分辨率已知时,可计算出星座的轨道高度。
h=
(5)
(2)轨道倾角约束
卫星对目标侦察的前提为卫星能够覆盖区域的最高点,卫星覆盖区域的最高纬度值取决于轨道倾角和卫星覆盖半角。根据卫星运动规律可知,卫星的纬度幅角为90°时,卫星覆盖区域的最高纬度值最大,为轨道倾角和卫星覆盖半角之和。考虑顺行轨道,已知目标区域最大纬度φmax,要保证卫星能够覆盖的区域最高点,其轨道倾角I需满足式(6)。
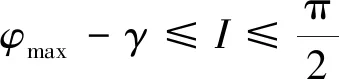
(6)
(3)升交点赤经和纬度幅角约束
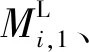
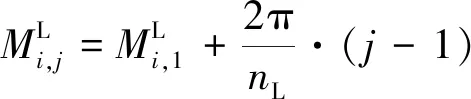
(7)
式中:i=1,2,...,N;j=1,2,...,nL,nL为轨道面内可见光卫星数量。

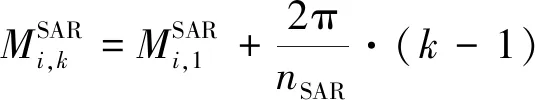
(8)
式中:k=1,2,...,nSAR,nSAR为轨道面SAR卫星数。
(4)卫星数量
设计星座同一轨道面内卫星均采用一箭多星方式发射。为保证同一等级区域内任意点的地面最低分辨率均一致,要求同一轨道面内所有卫星过境时对该区域100%覆盖,采用同轨多星覆盖域拼接的方法可确定目标区域被单轨面内卫星100%覆盖所需的最小卫星数。单轨面内卫星穿越目标区域最小纬度圈时的覆盖情况如图3所示,为保证图像的完整性,要求相邻可见光卫星的覆盖重叠域宽度为单颗卫星覆盖域宽度的10%,根据图3中几何关系可计算出单轨道面内可见光侦察卫星的最小数量nLmin,如式(9)所示。
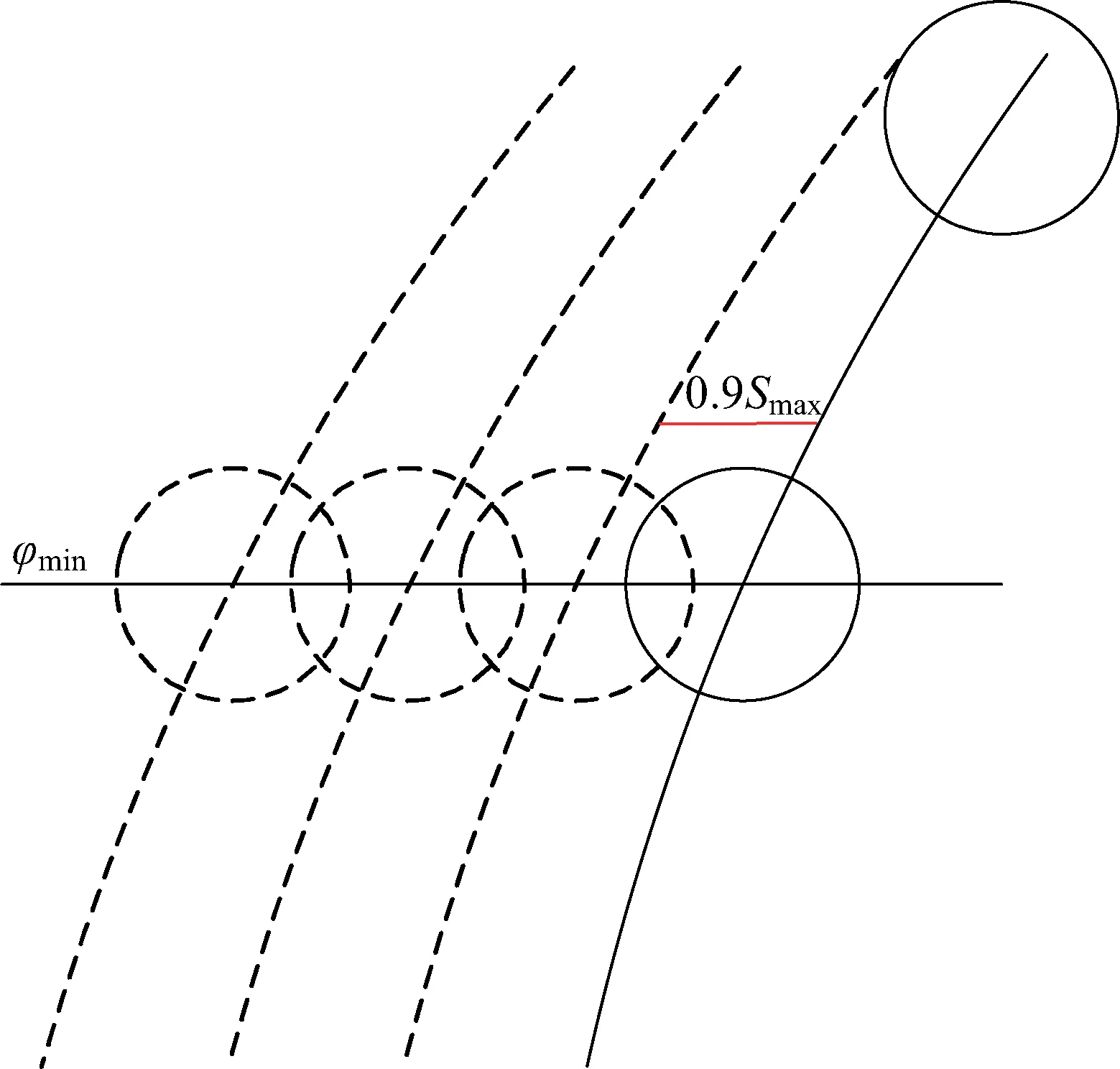
图3 覆盖域拼接Fig.3 Splicing coverage area
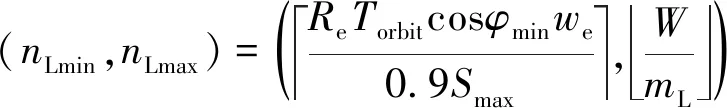
(9)
式中:Smax=2Reγ为卫星覆盖宽度;Torbit为轨道周期;we为地球自转角速度;φmin为目标区域最小纬度值;「x⎤为对x向上取整;⎣x」为对x向下取整。
已知火箭最大载质量为W,可见光卫星质量为mL,SAR卫星质量为mSAR。当一个轨道面内存在nL颗可见光卫星和nSAR颗SAR卫星时,轨面内卫星总质量不超过火箭最大载重量,需满足式(10)。综上,单轨道面内可见光卫星数量nL的取值范围为(nLmin,nLmax),SAR卫星数量nSAR的取值范围为(nSARmin,nSARmax),如式(11)所示。
nLmL+nSARmSAR≤W
(10)
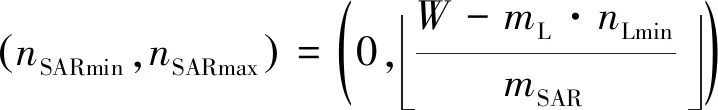
(11)
(5)光照约束
已知地面目标的赤经赤纬为(λT,φT),太阳的赤经赤纬为(λs,φs),根据向量夹角关系可得地面目标的太阳高度角χ,如式(12)所示。
χ=arcsin[cosφTcosφscos(λT-λs)+sinφTsinφs]
(12)
当地面目标的太阳高度角小于π/2时,地面目标处于光照条件下,可见光侦察卫星才能工作。
(6)升交点漂移同步约束
由设计需求可知,Ⅰ、Ⅱ、Ⅲ类区域的地面最低分辨率要求不同,其轨道高度将会存在差异。由于地球非球形摄动,卫星轨道升交点赤经存在漂移现象,尤其对于轨道高度和倾角不一致的星座,其升交点赤经漂移速度不一致,将导致星座覆盖性能不稳定,可通过对不同子星座的卫星设置一定轨道的倾角差来补偿因轨道高度不同导致升交点漂移速率差。
已知基础星座的轨道高度为h3,轨道倾角为I3,子星座1轨道高度为h2,轨道倾角为I2,子星座2的轨道高度为h1,轨道倾角为I1,若要满足升交点漂移速率同步,需满足式(13)。升交点漂移速率计算公式如式(14)所示。

(13)
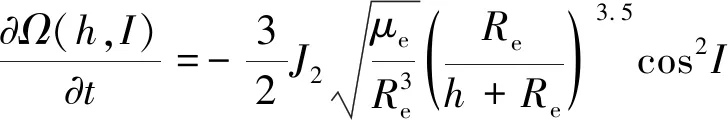
(14)
式中:Ω为升交点赤经;J2=1.0826261×103为地球非球形摄动参数;μe为地球引力常数。
4.2 基础星座优化设计模型
假设基础星座共存在N个轨道面,按照升交点赤经大小顺序分别编号为(1,2...,N),N个轨道的升交点赤经平均分布于(0,π)范围内,第1个轨道面的升交点赤经为Ω1,其取值范围为(0,π/N),则第i个轨道面的升交点赤经可表示为Ωi,如式(15)所示。

(15)
优化模型中共存在2N+4个优化变量,N为轨道面数,其中2个整数变量和2N+2个实数变量,整数变量为轨道面内可见光卫星数量和SAR卫星数量,实数变量包括第1个轨道面的升交点赤经,第i个轨道面内第1颗可见光卫星的纬度幅角、第i个轨道面内第1颗SAR卫星的纬度幅角和轨道倾角。
优化目标:
min[R3(x),C3(x)]
式中:R3(x)为基础星座对整个目标区域的最大重访时间;C3(x)为基础星座的成本。
优化变量:
约束条件:
可见光卫星对地侦察时需满足光照条件才能工作。
优化步骤如下:
步骤 1:设定初始星座轨道面数N=1。
步骤2:建立星座优化模型,选用改进的MOPSO算法对模型进行求解。
步骤 3:判断非支配解集中是否满足以下条件的可行个体,1)最大重访时间小于等于Ⅲ类区域最大重访时间阈值;2)基础星座成本最小;若存在,输出该解;若不存在,轨道面数增加1,重复步骤2~3。
4.3 子星座1设计模型
对基础星座设计模型求解后可得基础星座的轨道高度h3和轨道倾角I3,根据Ⅱ类区域的最低地面分辨率设计要求,可计算出子星座1的轨道高度h2,再根据升交点漂移速率同步约束,进一步计算出子星座1的轨道倾角I2。子星座1优化设计过程中共有3N+2个优化变量,N为轨道面数,其中存在2个整数变量和3N个实数变量,整数变量为轨道面内的可见光卫星数量和SAR卫星数量,实数变量为第i个轨道面的升交点赤经、第i个轨道面第1颗可见光卫星和第1颗SAR卫星的纬度幅角。
优化目标函数:
min[R2(x),G2(x),C2(x)]
式中:R2(x)为星座对Ⅱ类区域的最大重访时间;G2(x)为星座对Ⅱ类区域的弹性指数;C2(x)为子星座1成本。
优化变量:
约束条件:
可见光卫星对地侦察时需满足光照条件才能工作。
优化步骤与基础星座类似,按轨道面数逐步递增进行优化,直到星座满足Ⅱ类区域的设计需求。
4.4 子星座2设计模型
子星座2的设计目的为提高星座对Ⅰ类区域的覆盖和弹性能力。同理,根据Ⅰ类区域的最低地面分辨率设计要求和升交点漂移同步约束可计算子星座2的轨道高度和倾角。子星座2的优化模型中共存在3N+2个优化变量,整数变量为轨道面内的可见光卫星数量和SAR卫星数量,实数变量为第i个轨道面的升交点赤经、第i个轨道面第1颗可见光卫星和第1颗SAR卫星的纬度幅角。
优化目标函数:
min[R1(x),G1(x),C1(x)]
式中:R1(x)为星座对Ⅰ类区域的最大重访时间;G1(x)为星座对Ⅰ类区域的弹性指数;C1(x)为子星座2成本。
优化变量:
为保证星座在添加子星座2后对Ⅱ类区域的弹性指数依然满足设计要求,添加约束条件:星座对Ⅱ类区域弹性指数小于等于Ⅱ类区域弹性指数设计阈值。其余约束条件及优化步骤与子星座1类似,不再叙述。
5 仿真示例分析
仿真时间为2020-01-01 00:00:00至2020-01-02 00:00:00。将目标区域按照重要程度分为Ⅰ类区域、Ⅱ类区域和Ⅲ类区域,各等级区域的性能指标要求如表1所示。

表1 星座设计指标要求
可见光侦察卫星参数设置:像元p=8 μm,焦距f=1 500 mm,卫星最大侧摆角α=28.5°,视场半角β=1.5°,卫星质量mL=120 kg。SAR侦察卫星参数设置:外侧视角40°,视场角20°,前后视角10°,卫星质量mSAR=200 kg。火箭最大载重量W=2.0 t。
5.1 星座设计案例
目标区域的最低纬度φmin=0°,最高纬度φmax=55°。由已知参数及理论分析可得基础星座部分参数为h=910.09 km,I∈(50.15,90),可见光侦察卫星数量范围为(3,16),SAR卫星的数量范围为(0,8)。
按照基础星座优化步骤进行优化,当轨道面数N=2时,存在满足条件的可行解。改进的MOPSO算法得到的非支配解集如图4所示。图4中箭头所指的点为满足设计要求的基础星座构型参数:2个轨道面,每个轨道面存在3颗可见光卫星,4颗SAR卫星,第1个轨道面的升交点赤经为79.64°,2个轨道面第1颗可见光侦察卫星的纬度幅角为95.56°、103.76°。2个轨道面第1颗SAR卫星的纬度幅角为28.01°、123.28°,轨道倾角为33.28°。
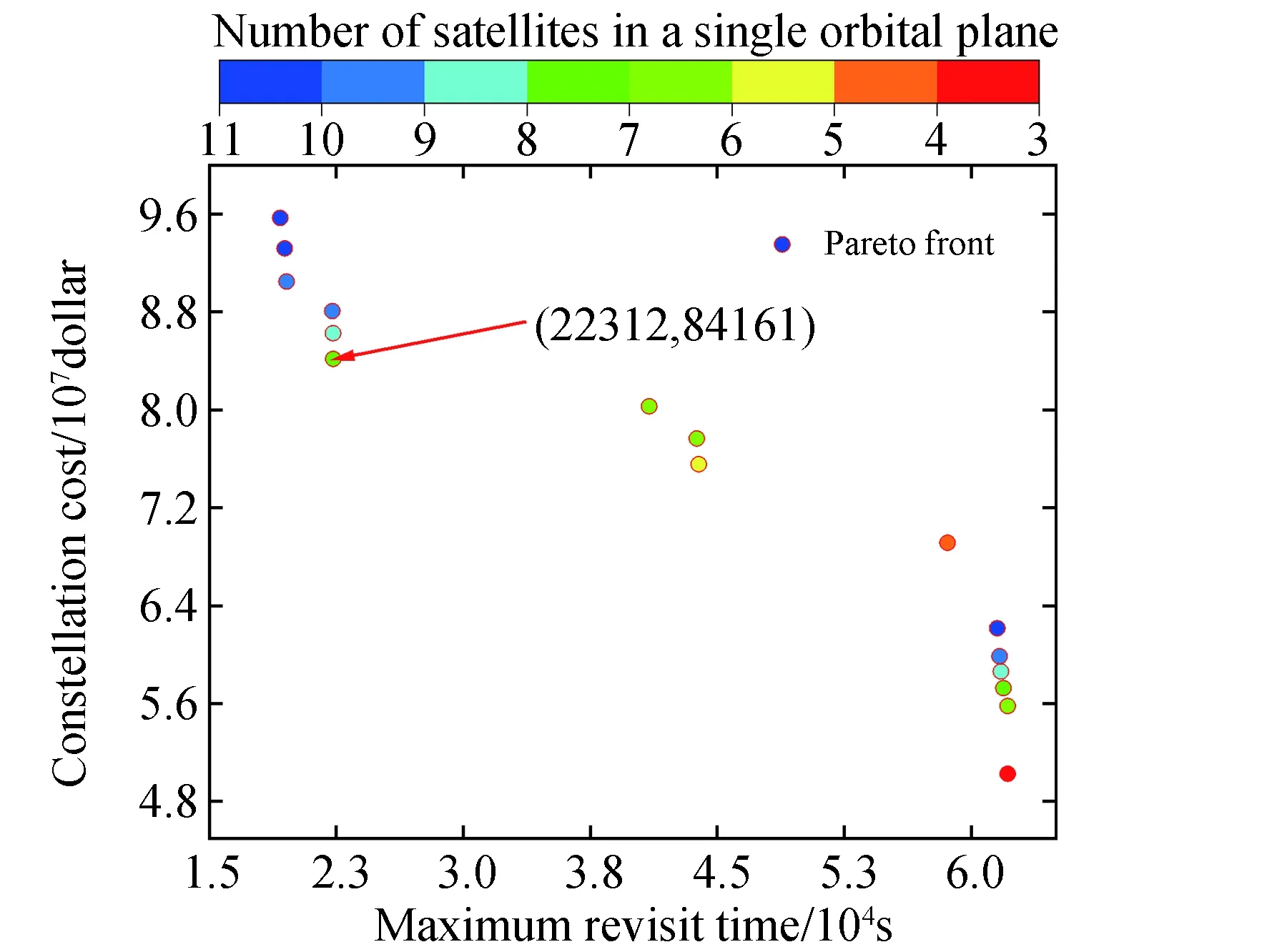
图4 2轨道面基础星座成本和最大重访时间权衡对比Fig.4 Cost and maximum revisit time comparison of 2-orbit basic constellation
计算得到基础星座对Ⅱ类区域取最大重访时间为21 844 s,降阶状态下最大重访时间为38 268 s,弹性指数为75.19%,由表1可知基础星座不满足Ⅱ类区域的设计需求,所以需设计子星座1提高星座对Ⅱ类区域的性能。
Ⅱ类区域的最低纬度为35.5°,由理论分析可得,子星座1的部分参数h=664.94 km,I=85.44°,可见光卫星数量范围为(4,16),SAR卫星数量范围为(0,7)。通过优化模型及步骤优化可得当轨道面数N=2时,存在满足条件的可行解,如图5所示。可行解集向XY平面投影得到的图像如图6所示。

图5 2轨道面子星座1成本、最大重访时间和弹性指数权衡对比 Fig.5 Cost ,maximum revisit time and elastic index comparison of 2-orbit constellation 1
图6中红色箭头所指的解向量为满足设计要求子星座1的星座参数:2个轨道面;每个轨道面4个可见光卫星,6个SAR卫星;2个轨道面的升交点赤经分别为:113.72°、40.78°;2个轨道面第1颗可见光卫星的纬度幅角为:71.27°、52.98°,2个轨道面第1颗SAR卫星的纬度幅角为37.38°、30.22°。
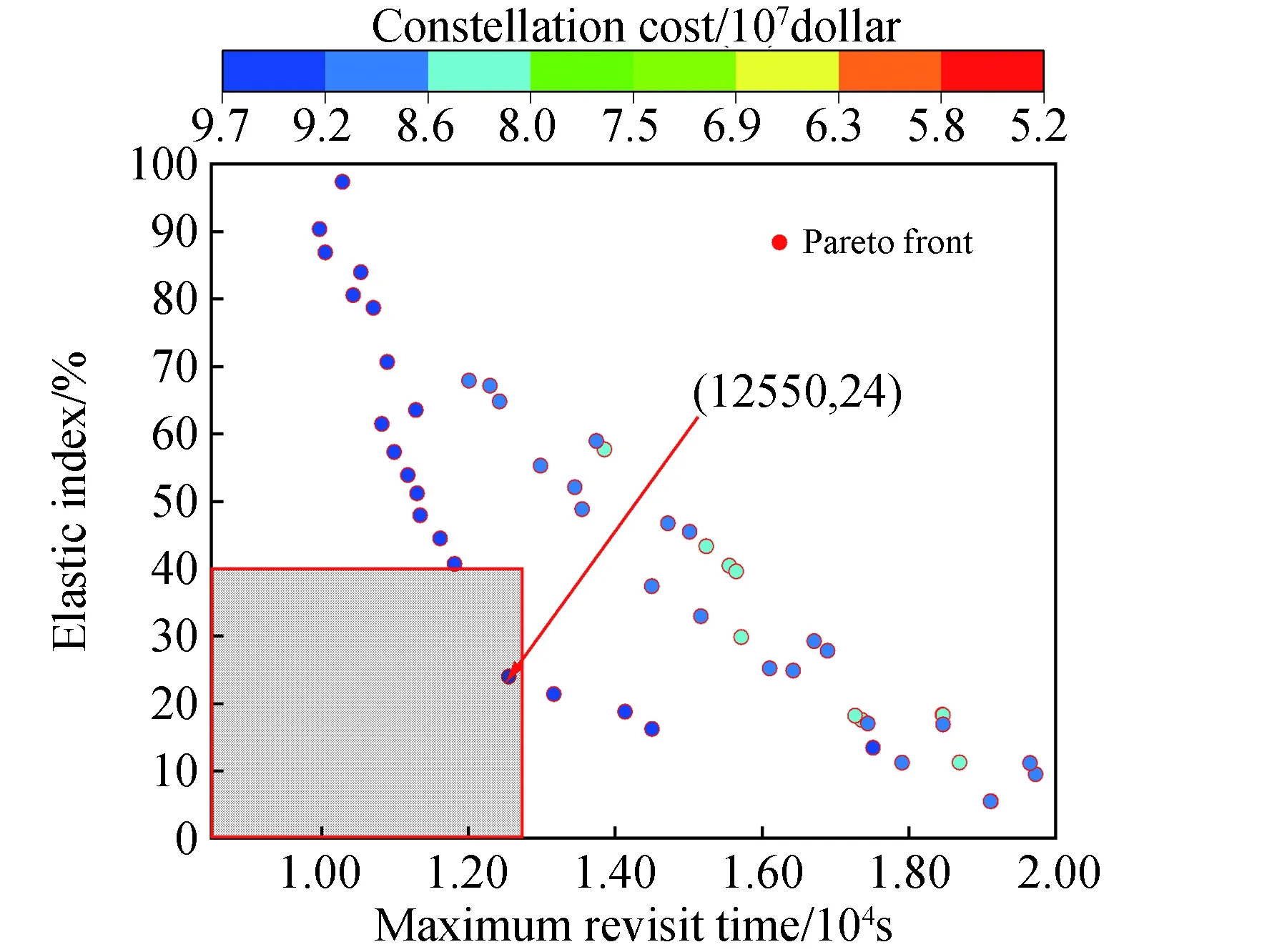
图6 2轨道面子星座1最大重访时间和弹性指数权衡对比Fig.6 Maximum revisit time and elastic index comparison of 2-orbit constellation 1
计算基础星座和子星座1组成的混合星座对Ⅰ类区域的最大重访时间为13 142 s,降阶状态下的最大重访时间为25 516 s,弹性指数为94.15%,由表1可知不满足星座对Ⅰ类区域的设计需求,需设计子星座2提升星座对Ⅰ类区域的性能。
已知Ⅰ类区域的最低纬度值为0°,由已知参数和理论分析可得子星座2的部分参数h=408.04 km,I=86.00°可见光卫星数量范围是(5,16),SAR卫星数量范围为(0,7)。根据优化模型及步骤进行优化,当轨道面数N=4时,存在满足条件的可行解,如图7所示。可行解集向XY平面投影得到的图像如图8所示。
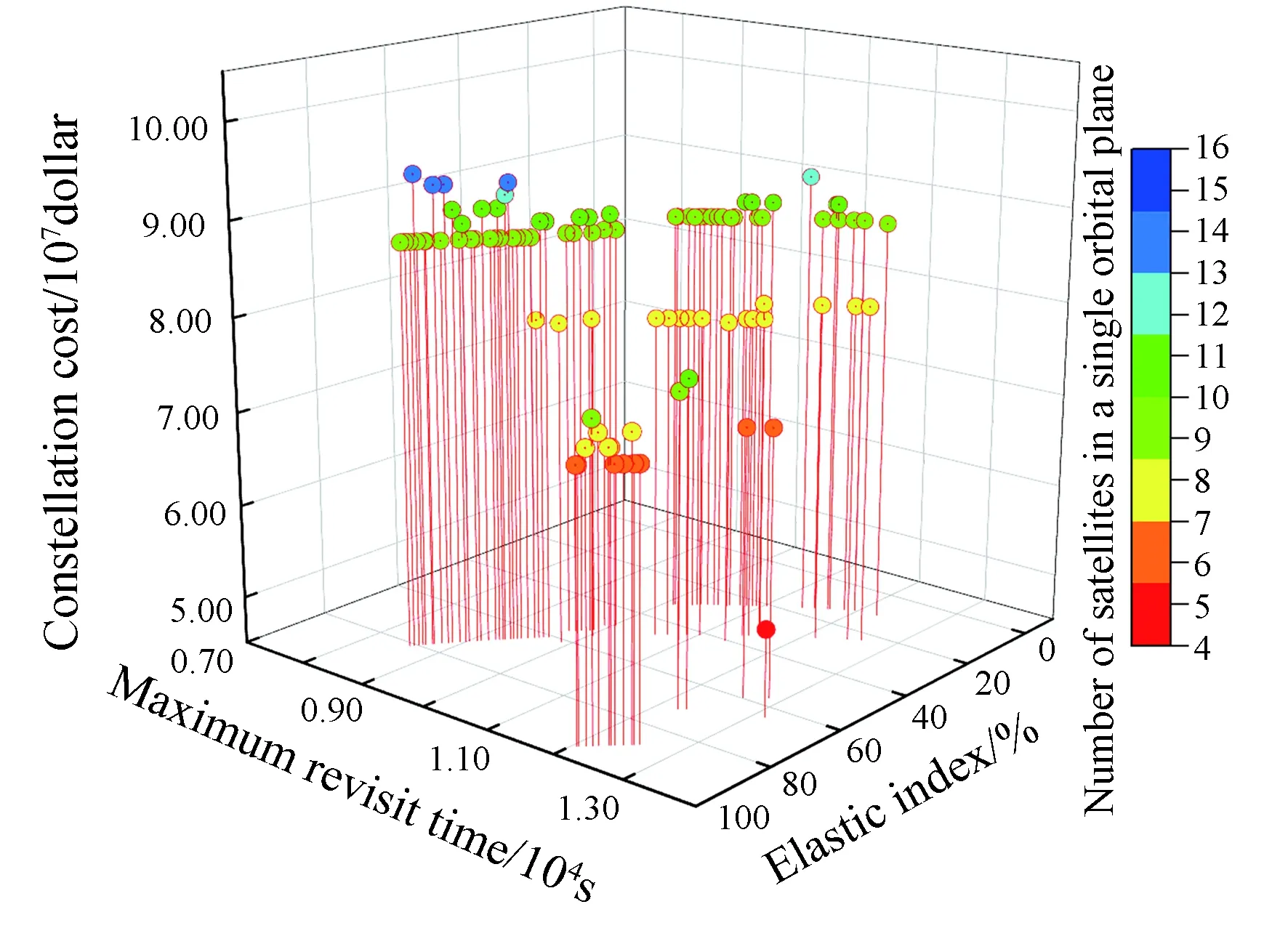
图7 4轨道面子星座2成本、最大重访时间和弹性指数权衡对比 Fig.7 Cost ,maximum revisit time and elastic index comparison of 4-orbit constellation 2
图8中红色箭头所指的解向量即为满足设计要求的子星座2星座参数:共4个轨道面,每个轨道面5颗可见光卫星、4颗SAR卫星;4个轨道面的升交点赤经分别为:128.33°、177.91°、52.63°、89.46°;4个轨道面第1颗可见光卫星的纬度幅角分别为:65.23°、70.13°、61.86°、57.11°;4个轨道面第1颗SAR卫星的纬度幅角为:68.79°、20.24°、83.29°、75.62°。
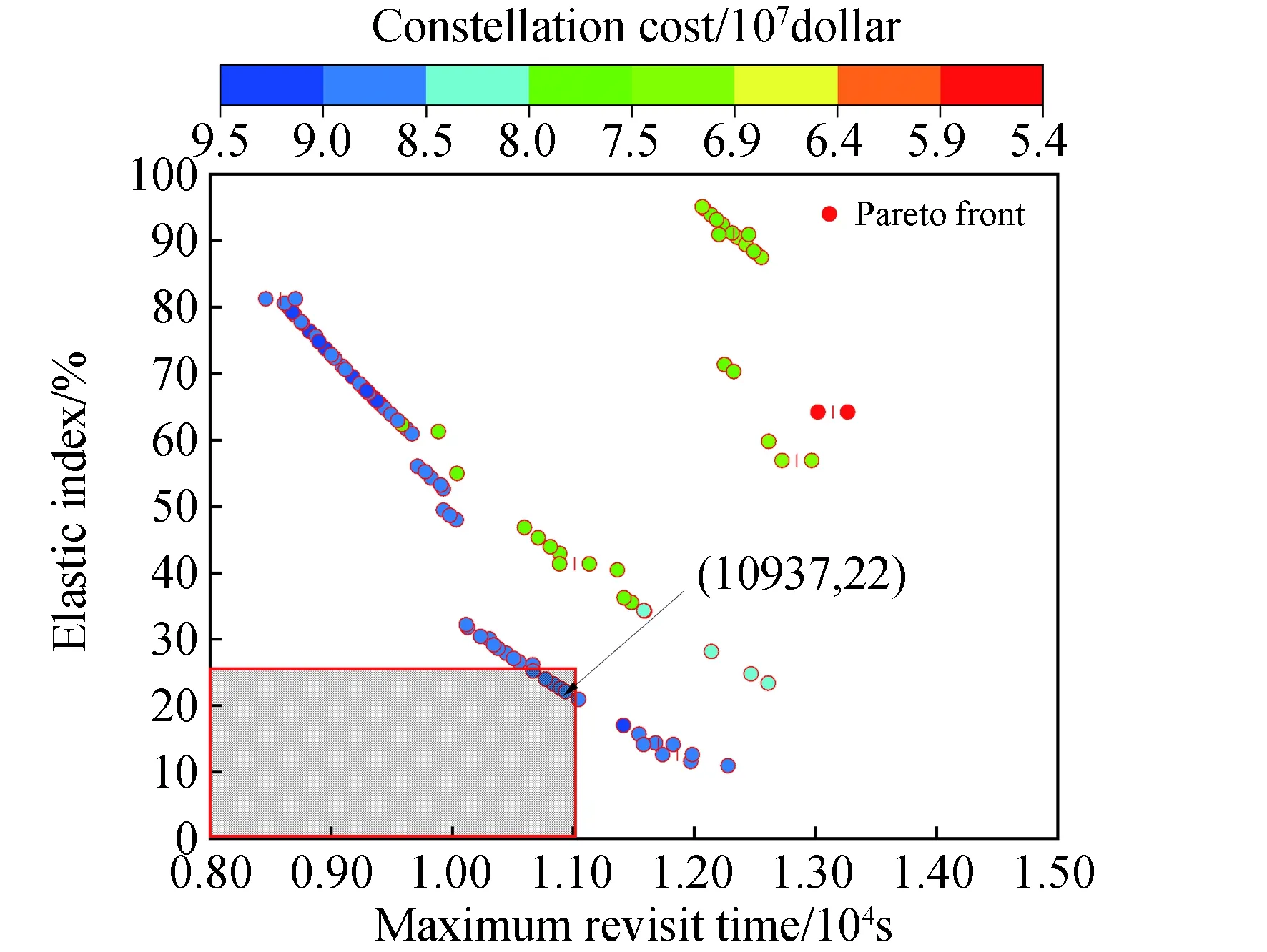
图8 4轨道面子星座2最大重访时间和弹性指数权衡对比Fig.8 Maximum revisit time and elastic index comparison of 4-orbit constellation 2
综上,最终目标星座是由基础星座、子星座1和子星座2组成的混合星座,共8个轨道面,70颗卫星。评估目标星座对Ⅰ类区域、Ⅱ类区域和Ⅲ类区域的覆盖性能,具体指标值如表2所示,由表1可知,目标星座对Ⅰ类区域、Ⅱ类区域和Ⅲ类区域的各项性能指标满足设计要求。

表2 目标星座对三类区域的各项性能
5.2 与Walker星座设计方法比较分析
为验证该类型星座及其设计方法的优越性,选择Walker型星座进行对比试验,目标区域、卫星参数、火箭参数均相同,由于Walker星座无法对区域分级,以上文中最高等级区域的设计指标要求作为Walker型星座对该目标区域的指标设计要求,按照Walker型星座构型对星座进行设计,Walker型星座的相位因子取1。建立优化模型并由改进的MOPSO算法对模型求解,可知当轨道面数为13时,存在满足设计要求的星座构型方案,优化过程如图9所示,图10为优化过程中产生的非支配解向XY平面的投影。
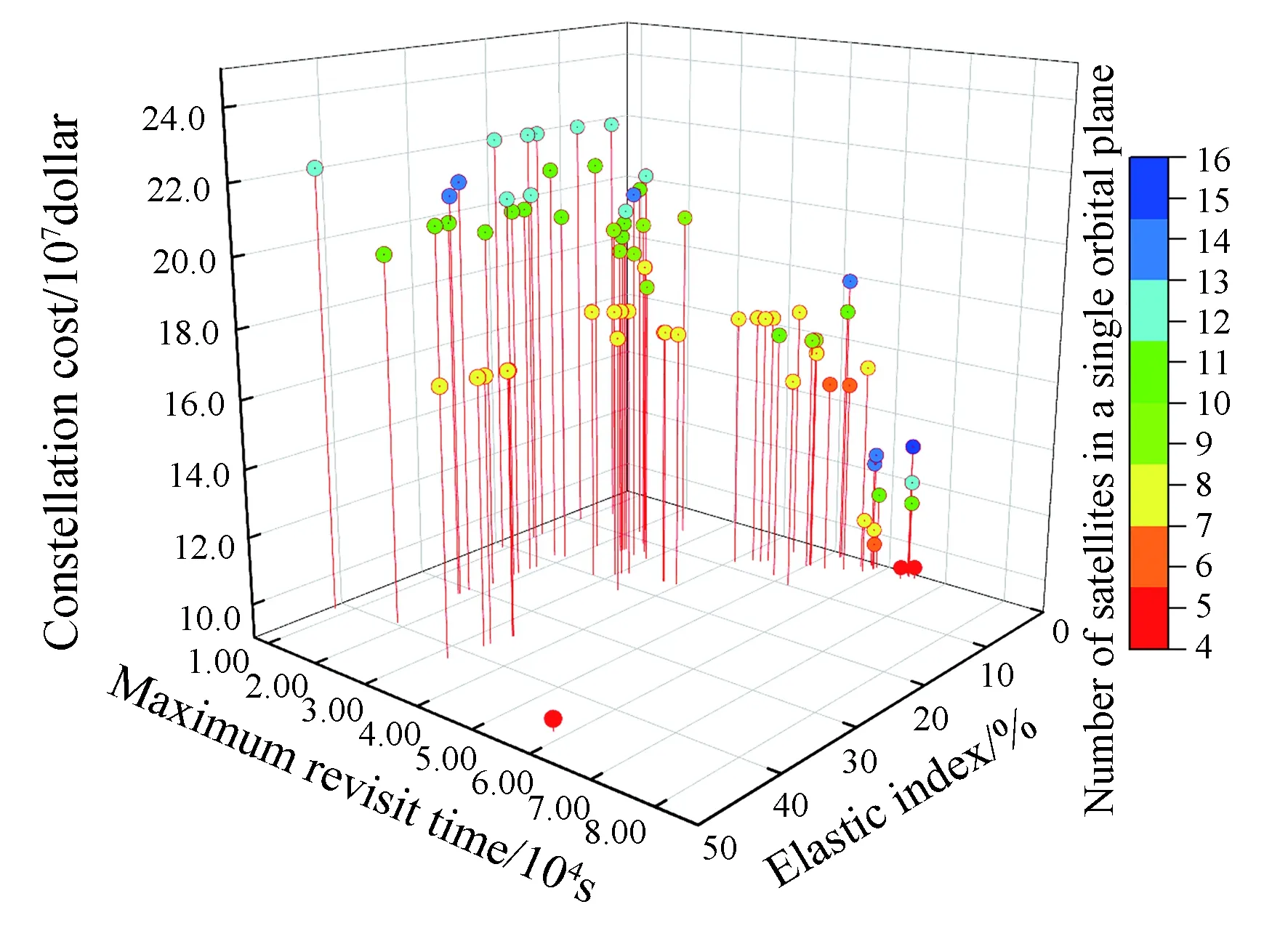
图9 13轨道面Walker星座成本、最大重访时间和弹性指数权衡对比Fig.9 Cost, maximum revisit time and elastic index comparison of 13-orbit Walker constellation
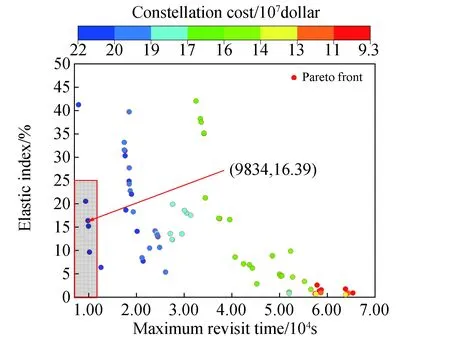
图10 13轨道面Walker星座最大重访时间和弹性指数权衡对比Fig.10 Maximum revisit time and elastic index comparison of 13-orbit Walker constellation
图10中箭头指向为最优星座构型,构型参数如下:轨道面数为13,每轨面内有5个可见光卫星和7颗SAR卫星,第1个轨道面的升交点赤经为3.66°,第1个轨道面内第1颗可见光卫星和第1颗SAR卫星的纬度幅角分别为41.05°、37.66°。
对比两种星座构型结果,可以看出多等级区域总卫星数为70,而Walker星座卫星数达156颗,高出其1倍之多。结果表明:相比Walker星座设计方法,多等级区域侦察星座设计方法对区域实现分级覆盖的同时,降低了星座成本,对区域内的目标更具有针对性。
6 结论
本文提出了多等级区域侦察弹性星座设计方法,并进行了仿真校验。结果表明:
1)利用该方法设计的多等级区域侦察弹性星座对Ⅰ、Ⅱ、Ⅲ类区域的最大重访时间为10 937 s、12 241 s、17 437 s,弹性指数为22.13%、24.20%、63.61%,实现了对不同等级区域覆盖能力和弹性能力分级,验证了设计方法的有效性。
2)在相同设计要求的前提下,对Walker星座进行设计,对比两类星座设计结果。结果表明所提出的设计方法不仅实现了对区域分级设计,还降低了星座的成本,对复杂区域目标更具有针对性,进一步证明了该设计方法的优越性。
3)下一步可将该类型星座应用于通信及导航任务中,也可以对该类型星座的重构方法进行研究。
