基于二次统计CFAR处理的目标径向尺寸估计

龚林 浣沙 张磊 盛佳恋

（1. 中山大学电子与通信工程学院软件化雷达技术研究室，广州 510006；2. 广州大学物理与电子工程学院，广州 510006；3. 上海无线电设备研究所，上海 201109）

引 言

随着雷达技术的发展，雷达工作带宽逐渐变大，由宽带雷达获得的目标回波经处理可得高分辨距离像(high resolution range profile, HRRP)[1]. HRRP中包含目标的几何结构信息，其中较为重要的是目标在雷达视线上的径向投影尺寸，其对目标的型号、大小粗分类[2-4]具有重要意义，因此，在HRRP中提取出目标的径向尺寸是一项重要工作.

径向尺寸提取关键在于找到HRRP中目标区域的起始位置和终止位置. 文献[5]提出了一种基于概率分布参数估计的尺寸估计法，通过参数估计法(如极大似然法)来估计目标尺寸，缺点是当缺少某类目标的训练数据时，无法直接从HRRP中测得目标尺寸. 文献[6]用噪声的平均水平乘以一个固定系数K来得到检测门限，缺点在于检测门限固定且K值难以确定. 文献[7-8]提出了一种基于自适应差分算子的径向尺寸提取法，运用自适应差分算子进行预处理可以抑制噪声，但文献中并没有提到径向尺寸提取的具体方法. 文献[9]先对HRRP减去噪声基底，以获得清晰的噪声-目标边界，再用阈值法确定径向尺寸；但是当目标的边缘信号较弱时易导致漏检，使得检测尺寸小于实际尺寸；当噪声区域有“野值”存在时，该方法也容易误判. 文献[10]提出了一种快速傅里叶变换(fast Fourier transform, FFT)-超分辨目标径向尺寸提取算法，需要用到多信号分类(multiple signal classification, MUSIC)算法、基于最小二乘的旋转不变技术信号参数估计(total least-squares estimating signal parameter via rotational invariance techniques, TLS-ESPRIT)算法等超分辨方法来提取目标信号点，缺点是对信噪比(signal-to-noise ratio,SNR)的要求较高且运算量较大.

针对以上问题，本文提出一种基于二次统计恒虚警(constant false alarm rate, CFAR)处理的目标径向尺寸估计方法，该方法特别对具备下述特性的HRRP有效：目标边缘弱信号点在HRRP中呈现连续较低的幅值，但又比噪声区平均幅值要高. 该方法先采用CFAR检测法从HRRP两端向中间检测，当检测器检测到可疑目标时，进行二次统计CFAR处理，采用弱信号积累准则进行判断，即连续检测到k个大于门限的点时，判断为目标. 前后两端分别检测到目标后，通过逻辑判断，将目标位置确定在幅值上升起始点所对应的距离单元，前后两端位置的差值即为目标径向尺寸. 对实验数据进行检测，结果表明，该方法可以有效避免目标边缘弱信号点的漏检，且受“ 野值”影响较小，能够准确地提取目标径向尺寸.

1 基于HRRP的尺寸估计原理

宽带雷达的距离分辨率小于目标尺寸时，目标的强散射中心会分布在不同的距离单元当中，形成一维HRRP，如图1所示. 设宽带雷达系统的距离分辨率为 ΔRx，目标区域在一维距离像中的起始点为Pb，终止点为Pe，则目标在雷达视线方向上的投影长度L为

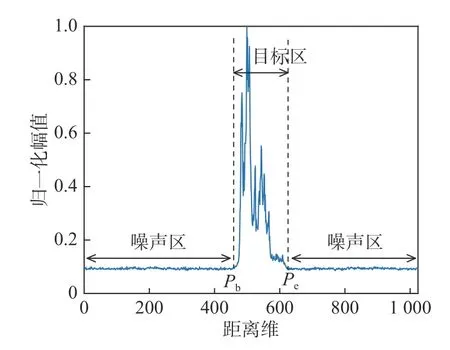
图1 距离像噪声区域与目标区域示意图Fig. 1 Schematic diagram of noise area and target area of range profile

2 CFAR检测法

CFAR检测是致力于在噪声干扰环境下提供可预知检测的技术，虚警率的定义是：在检测过程中，由于噪声存在，实际不存在目标的情况却被误判为存在目标的概率. 不同于窄带雷达目标检测中的双门限CFAR检测[11]，宽带雷达中常采用邻近单元平均CFAR检测法[12]，其基于以下假设：邻近单元所含杂波的统计特性与待测单元的一致(称为均匀干扰)，故待测单元的杂波统计特性可从邻近单元估计得到.对于基本的CFAR检测过程，主要是对检测单元的噪声电平进行估计，并根据估计值设置检测阈值，再将阈值与检测单元的信号电平进行比较，以判断是否有目标.

如图2所示，CFAR检测的滑窗包括：检测单元、保护单元和参考单元，其中参与检测单元阈值计算的只有参考单元；保护单元的作用是防止参考单元中出现目标点，否则会过度抬高检测门限，导致漏检，因此保护单元不参与门限计算. 本文分别采用前置CFAR和后置CFAR来进行目标前端和后端的检测，前置CFAR只有左半检测窗，而后置CFAR只有右半检测窗. 设虚警率为Pfa，参考单元个数为M，参考单元内的噪声平均功率为，则检测阈值T由下式确定[13]：

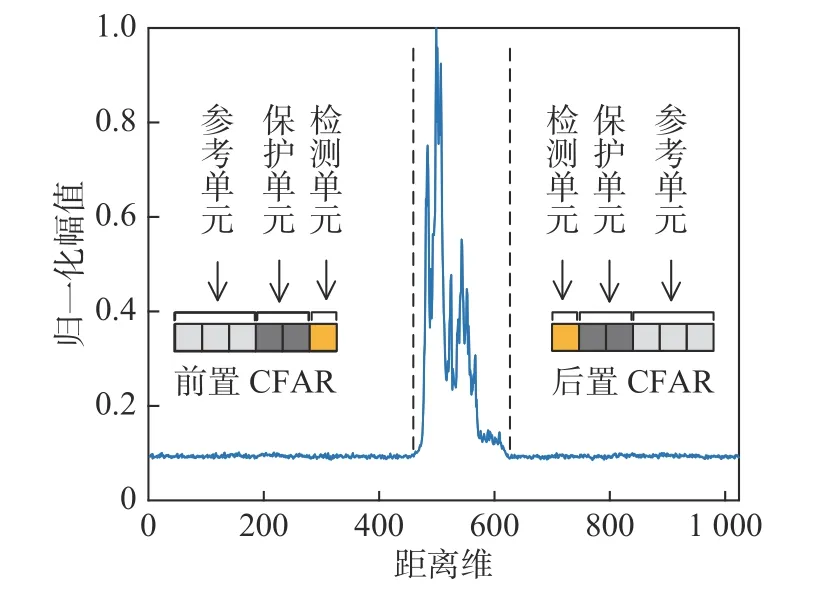
图2 一维距离像及前/后置CFAR检测窗示意图Fig. 2 Schematic diagram of range profile and front/rear CFAR detection window

将求得的检测阈值T与检测单元比较，从而做出目标存在与否的判决，当前/后置CFAR中的检测单元幅度大于门限值T时，说明可能检测到了目标，但也可能是“野值”或噪声引起的误判，因此需进行基于弱信号积累准则的判断.

3 弱信号积累判断准则

本文方法针对一种目标弱信号点在HRRP中呈现连续较低的幅值但又比噪声区平均幅值要高的特殊情况进行处理，如图3所示. 为避免目标的边缘弱信号点漏检，就要在CFAR检测时降低检测门限(对应调高CFAR的虚警率). 当虚警率增高时，传统的CFAR检测法容易因误判提前在噪声区停止检测，原因是传统的CFAR检测在检测器首次检测到大于门限的点时就停止检测，此时真实情况可能是由于噪声突变引起的误判，所以本文以连续检测到多个弱信号点为检测标准，对CFAR检测进行优化，可有效避免目标边缘弱信号点的漏检和“野值”所导致的误判.

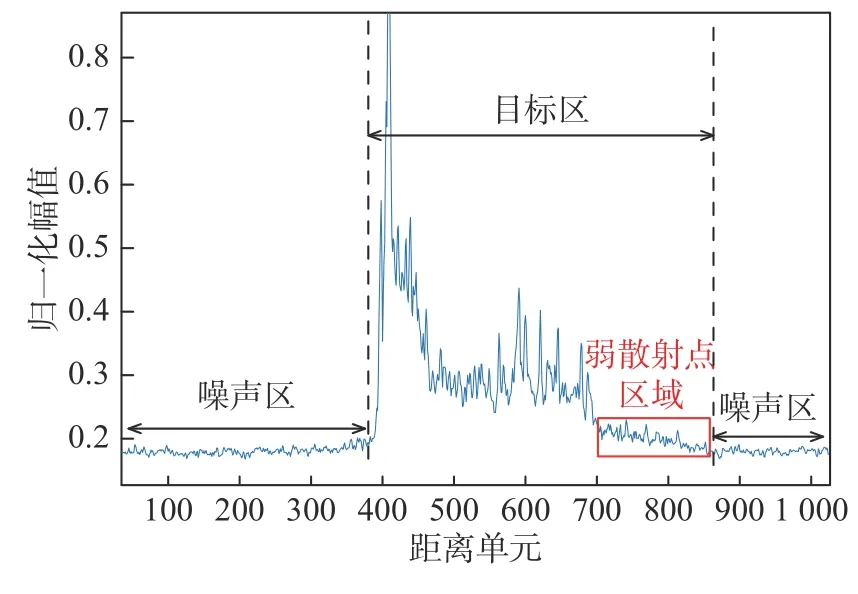
图3 带有弱信号点的HRRP示意图Fig. 3 Schematic diagram of HRRP with weak signal

基于CFAR检测法，可知检测过程中虚警率恒定，若将检测事件依次设为t0,t1,···,tk，每次检测的虚警率都为Pfa，由于每次检测之间相互独立，根据概率论知识，连续k次发生虚警的概率为

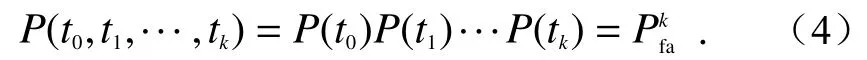
由于虚警概率Pfa∈(0,1)，累乘后的联合概率将是一个很小的值，也即连续发生虚警事件近乎为不可能事件，反之，则认为这并非发生了虚警，而是真实地检测到了目标. 当前/后置CFAR检测器连续检测到k个大于检测阈值的幅值时，则判定为检测到了目标，将这k个幅值点中的第一个取为目标区的起始点P′b/ 终止点P′e.

保护单元的设置使相邻待测点的噪声水平相差很小，当检测器检测到可疑点时，可用首个可疑点的检测阈值近似后续待测点的阈值，但以相同阈值作判决时，弱信号积累准则易将边缘点判为噪声. 对此本文的策略为：当检测到可疑点时，以首个检测门限为基准，以斜率s衰减后续的检测门限，即用衰减后的门限来进行弱信号积累准则的判断.

设首个检测到可疑目标的门限为T0，则连续判断k次的阈值分别为

如图4所示，以相同门限进行判决时(图(a))，由于HRRP边缘弱点的特性，点数积累判断条件不易满足，从而导致误判，将阈值以一定的斜率作衰减再进行判断可降低误判概率(图(b)).

采用上述检测步骤时，测得的目标位置一般在目标区上升沿，通过逻辑判断，将目标位置确定在上升起始点，可使检测边界更靠近噪声-目标分界处，优化后的目标径向尺寸更接近真实值. 边缘优化后目标区起始点更新为Pb，终止点更新为Pe，起始终止两点差值即为目标区长度. 以前置CFAR边缘优化为例，边缘优化如图5所示.

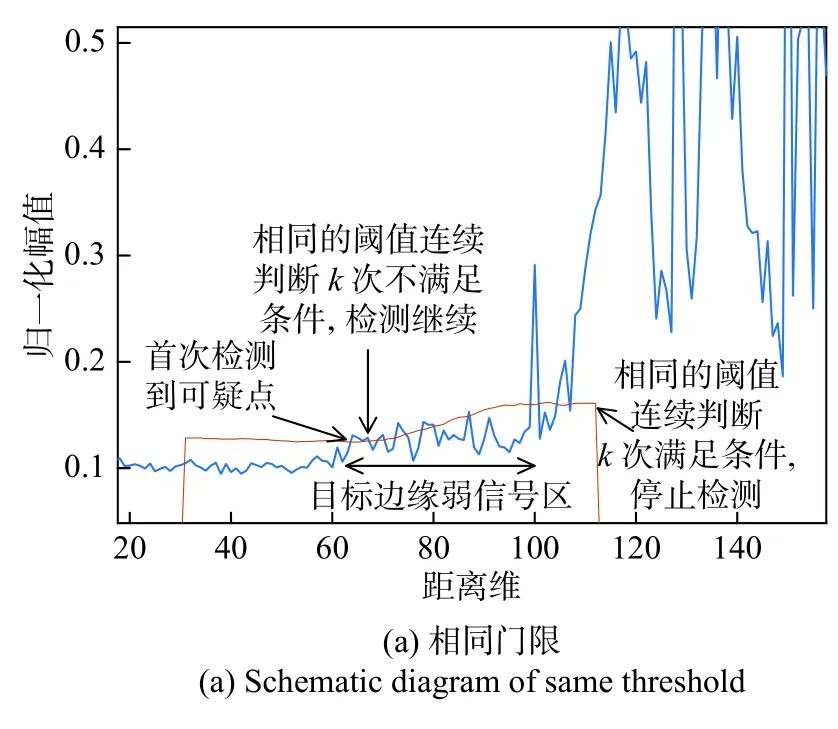
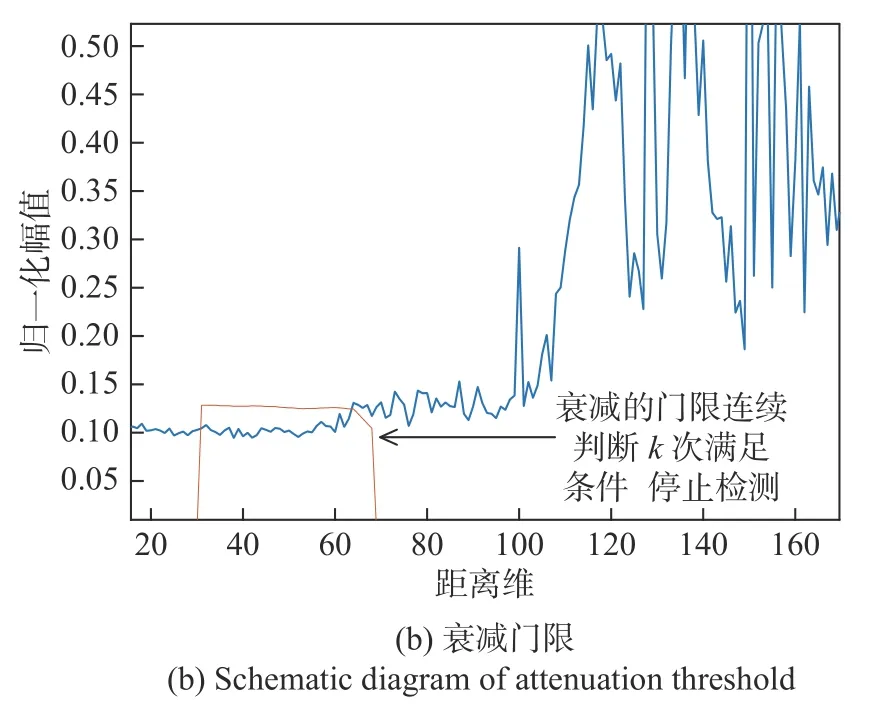
图4 相同门限与衰减门限弱信号积累判断准则对比Fig. 4 Comparison of weak signal accumulation judgment criteria between the same threshold and the attenuation threshold

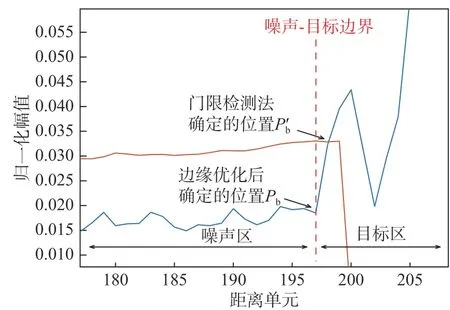
图5 边缘优化示意图Fig. 5 Edge optimization diagram

图6给出了本文的目标尺寸估计算法流程，该算法的完整步骤总结如下：

1)分别用前、后置CFAR从HRRP的两边向中间滑动检测.

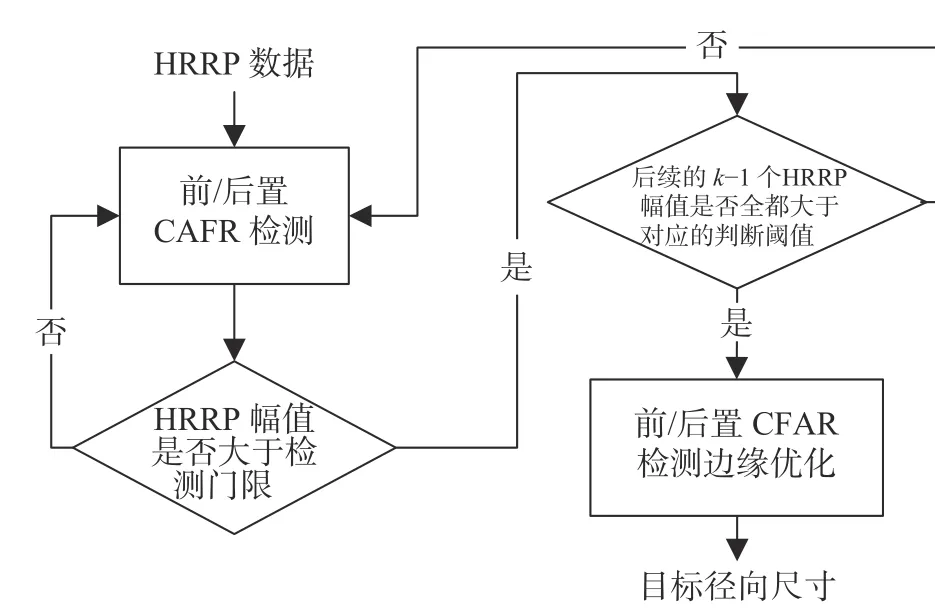
图6 基于二次统计CFAR处理的目标径向尺寸估计法算法流程Fig. 6 Algorithm flowchart of target length estimation based on quadratic statistical CFAR processing

2)当检测到大于阈值的可疑目标时，进行基于弱信号积累准则的判断，若连续检测到k个大于阈值的点，则判定为目标.

3)进行边缘优化，将检测器截取的上升沿所对应的距离单元更新为上升起始点所对应的距离单元，前后两端的差值即为目标尺寸.

4 实验分析

实验数据为实测的一维距离像，通过添加高斯白噪声的方法来改变其SNR，再分别用本文所提出的尺寸提取法与文献[9]中尺寸提取法和传统CFAR阈值检测法进行检测对比，在相同的虚警率条件下，对实验数据进行尺寸估计.

在CFAR检测中，参考单元数量为M的条件下，SNRRSN、检测概率Pd和虚警概率Pfa之间满足[14]：

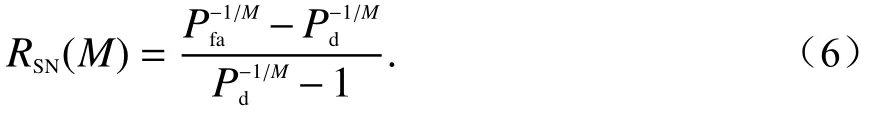
相对误差为

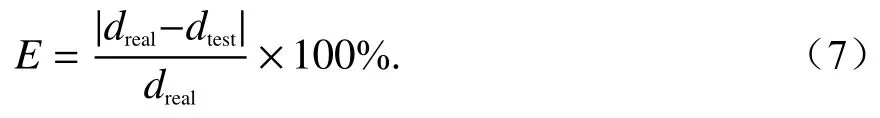
式中：dreal为目标实际尺寸；dtest为算法测得尺寸.

样本1和样本2的检测参数设置如表1所示.

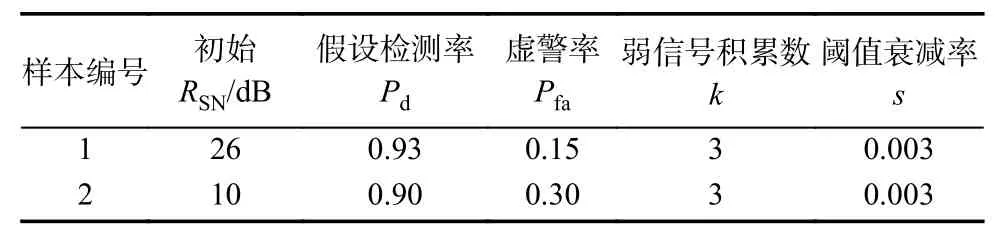
表1 基于二次统计CFAR处理的尺寸估计检测参数设置Tab. 1 Parameter setting of size estimation detection based on quadratic statistical CFAR processing

对于样本1，设M=20，k=3，Pd=0.93，s=0.003，样本1的检测结果比较如图7所示. 图(a)中，初始SNR为26 dB时，根据式(6)可设置Pfa=0.15，此时三种方法都有较好的检测效果. 图(b)中，当Pfa不变，SNR减小到10 dB时，两种对比算法因过大的噪声已提前停止检测，而本文提出的检测方法仍有较好的检测效果. 图(c)为三种方法测量相对误差，当SNR大于10 dB时，弱信号积累法的检测相对误差较小且具有稳健性，而两种对比算法在同样的虚警率设置下，SNR小于23 dB时就已失效. 图(d)～(f)给出了本文检测方法在不同Pfa和k条件下对样本1的检测性能对比.k∈[3,5]且Pfa=0.15时，具有较好的检测效果；k>5时，低SNR条件下的检测效果有所下降，原因是积累点数过多，使目标边缘点被判定成噪声，继续检测将会过度抬高检测阈值，导致目标点漏检.

图7 样本1的检测结果比较Fig. 7 Comparison of detection results of sample 1

样本2是一个边缘弱信号幅值大于噪声区幅值的典型样本，570～630距离单元上的距离像为目标边缘弱信号点，其检测结果如图8所示. 设Pd=0.9，图(a)中，初始SNR为10 dB时，根据式(6)设置Pfa=0.3，三种算法都能正确提取出目标的径向尺寸.图(b)中，SNR降至7 dB时，两种对比算法就已失效.图(c)为三种方法测量相对误差，SNR小于10 dB时，两种对比算法已失效，当SNR下降到7 dB前，本文方法仍有较好的检测效果. 图(d)～(f)给出了本文检测方法在不同Pfa和k条件下对样本2的检测性能对比. 可以看出：当k=3、4且Pfa=0.3时，在高SNR条件下算法具有良好性能，当SNR小于6.5 dB时算法的检测性能开始下降；当k=5且Pfa=0.3时，算法的准确性和稳健性最佳. 综上所述，当k=5时检测效果最佳.

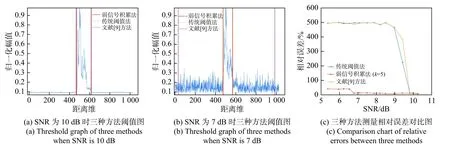
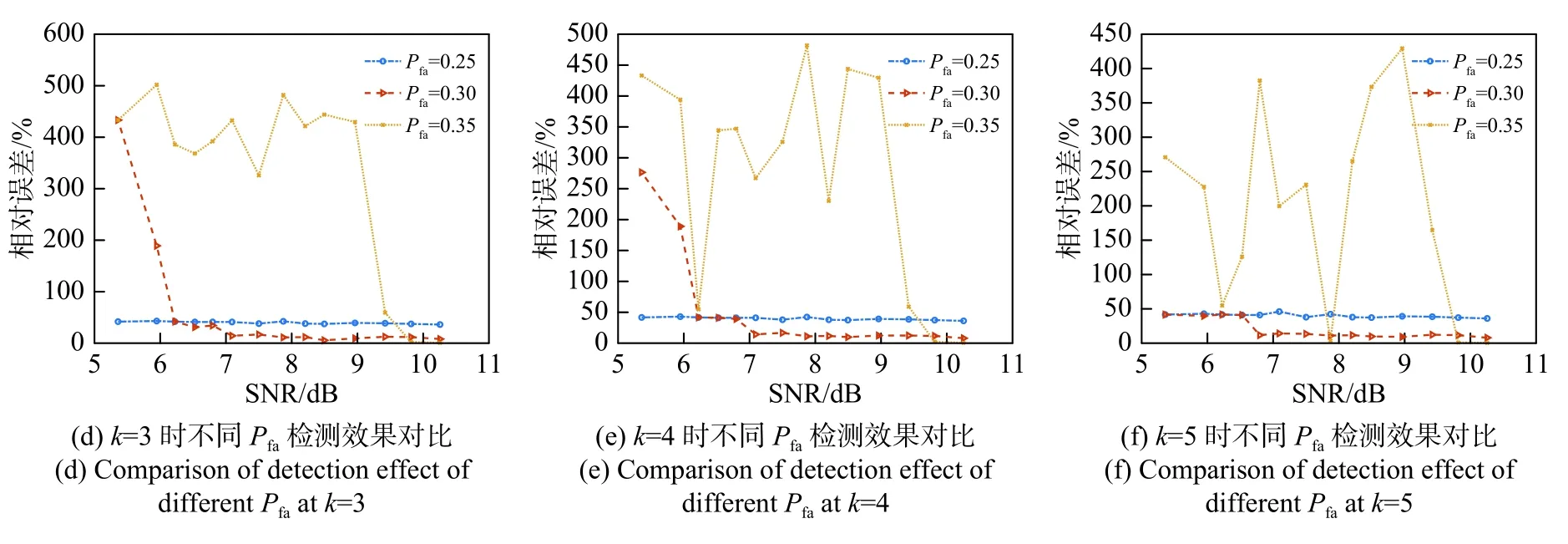
图8 样本2的检测结果比较Fig. 8 Comparison of detection results of sample 2

图9给出了样本2在Pfa=0.3和k=5的最佳检测条件下不同阈值衰减率s的检测效果. 当s∈(0.003,0.004)时，算法的准确性和稳健性最佳，s≥0.006时，检测效果开始变差，原因是过高的衰减率易导致噪声和“野值”被判断为目标. 在s=0.002条件综上所述，s∈(0.003,0.004)时，检测效果最佳.下，当SNR小于8 dB时检测的稳健性开始下降，原因是过低的衰减率易导致检测器将目标判为噪声.

图9 样本2不同s条件下的检测对比Fig. 9 Detection comparison of sample 2 under differentthreshold attenuation rates

图10所示为边缘优化前后检测到的边界对比.可以看出，优化后的检测边界更靠近噪声-目标边界.

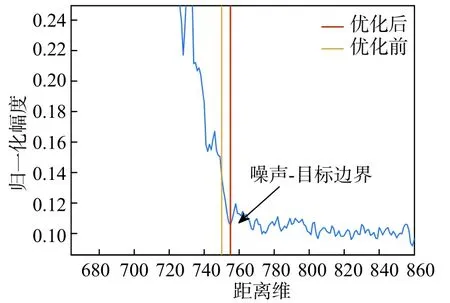
图10 边缘优化前后检测边界对比Fig. 10 Comparison of detection boundary before and after edge optimization

图11所示为边缘优化前后的误差对比. 可以看出，优化后94%样本的测量相对误差变得更小，个别样本的测量误差会稍增大. 原因是当优化前的检测边界已经取到噪声区域时，边缘优化会让检测边界更加远离噪声-目标边界，使测量尺寸略大于实际尺寸.

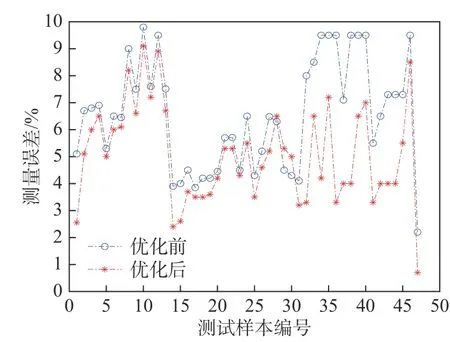
图11 边缘优化前后误差对比Fig. 11 Comparison chart of detection error before and after edge optimization

5 结 论

针对常规算法易受“野值”影响，SNR较低时，检测效果易受噪声突变影响，而降低检测虚警率又容易导致目标区边缘弱点漏检的情况，本文提出了一种基于二次统计CFAR处理的目标径向尺寸估计方法，给出了相关数学原理和具体操作步骤. 通过实验表明：对于边缘弱点连续且高于噪声平均幅值的HRRP情况，在低SNR条件下，该方法可有效避免弱信号点的漏检，并且可避免“野值”和噪声突变的影响，能快速精确地提取具有上述特征一维距离像中目标的径向尺寸特征. 提取的径向尺寸信息可以进一步为雷达目标识别提供粗分类的依据，具有一定的工程应用价值.