基于矩阵指数法的双线性Z变换PML模拟FDTD地下探测与成像

冯乃星 张玉贤 郑宏兴 曾庆生 童美松

（1. 深圳大学，深圳 518060；2. 河北工业大学，天津 300401；3. 南京航空航天大学，南京 210016；4. 同济大学，上海 200092）

引 言

在现代通信中，空中的无线电波可以为无线电、雷达、导航系统和其他应用传送信息[1-4]. 然而，在波长较短的无线电波中发现了局限性[5]，其信号在传播越来越远时变得越来越弱，甚至从不通过水传播，并且容易被岩层阻止. 例如，GPS[5]信号不能穿透水、土壤或建筑物墙壁，甚至不能传播到这些物体中. 因此，海底或地下活动，如矿产勘查，不能采用GPS信号. 此外，GPS和其他无线电信号在室内或摩天大楼之间的通信中表现出相当低的工作性能.

为了克服上述问题，可以将波长较长的甚低频(very low frequency, VLF)无线电视为一种有效的方法[6]. 众所周知，VLF波具有远距离传播和强大的能量穿透能力的优点[7]，它可以在水和地球表面上传播和跨越数百英尺，在空气中传播和跨越数千英里. 目前，VLF信号已广泛应用于军事和民用领域，如海底通信、远程通信导航、无线心率检测、地球物理研究和救灾等. 在所有的应用中，时域有限差分(finitedifference time-domain, FDTD)数值模拟中，对于VLF地球物理勘探的研究很少，因为对于三维VLF地下传感的完全匹配层(perfectly matched layer,PML)的吸收特性的研究在文献中是相当少见的.

据我们所知，FDTD方法作为一种高效的求解工具[8-9]，在求解Maxwell方程时受到了广泛的关注[10]，它可以基于一个简单的公式来避免复杂的渐近或格林函数. 目前，FDTD已被广泛应用于解决天线、波导、传播、散射等各种电磁问题[11-12]. 然而，由于计算机资源的限制，FDTD方法需要采用吸收边界条件(absorbing boundary condition, ABC)来模拟任意开域问题[13]. 作为最流行和最著名的ABC之一，Bérenger于1994年首次提出的PML是一种高效的吸收材料ABC，它可以终止由非均匀、色散、各向异性甚至非线性介质组成的FDTD问题[14].

随着Bérenger的开创性工作的演变，拉伸坐标PML(stretched coordinate PML, SC-PML)和各向异性PML(uniaxial anisotropic PML, UPML)作为两种可供选择的PML实现，是由Chew等人[15]和Sacks等人分别提出的[16]，且得到了非常广泛的应用. 然而，如文献[17-18]所述，这些SC-PMLs和UPMLs在减少后期反射和衰减低频隐失波方面效果非常差.

为了改善上述传统PML的缺点[19]，文献[20]提出了通过简单地将频率相关的极点从实轴移到复虚半平面来实现复频率偏移PML(complex frequency shifted PML, CFS-PML)的方法，其在衰减低频隐失波和减少后期反射等方面的高效性能，引起了人们的广泛关注. 随后，Berenger从理论上进一步解释了CFS-PML能够提高隐失波吸收的原因. 此外，通过在CFS-PML方法中采用递归卷积(recursive convolution, RC)技术，Roden等人开发了卷积PML(convolutional PML, CPML)，其具有与传统PML相似的计算效率[21]. 然而，由于在CPML公式中使用了不适当的时间步同步，所提出的CPML整体吸收能力在某些数值情况下有些退化. 为了解决这一问题，分别基于双线性Z变换(bilinear Z-transform, BZT)方法[22-23]、零极点匹配Z变换(matched Z-transform,MZT)方法[24]、递推积分[25]、辅助微分方程(auxiliary differential equation, ADE)法[26]、直接Z变换(direct Z-transform, DZT)方法[27]、分段线性RC(piecewise linear RC, PLRC)[25]、时间同步[28]，以及基于积分的指数时间差分(integrate exponential time difference,IETD)[29]的几种具有较高吸收效果的改进型PMLs.

虽然上述PML的吸收性能得到了改善，然而迭代形式复杂、效率较低. 为了解决这一问题，文献[30]提出了一种基于矩阵指数(matrix exponential, ME)方法的CFS-PML实现方案，该方案具有较高的精度，并为平面倒F天线(planar inverted-F antenna, PIFA)的应用保持了良好的效率. 然而，此文献中只有一个PIFA案例用于反映和分析其性能，所以我们不知道是否也可以计算其他问题并获得良好的结果. 因此，为了展示基于ME的PML实现在不同应用中的通用性，我们考虑了更多的情况.

本文提出了一种基于ME方法的CFS格式的高效、准确的BZT-PML方法，并将其应用于VLF地下传感问题. 另一方面，除了地下传感之外，还利用甚高频(very high frequency, VHF)地下成像问题来验证所提公式的完整性和稳健性. 该提案称为BZTME-PML. 由于采用了BZT方法，频域的乘法和时域的卷积均对应于Z域的乘法. 该方案结合了ME和Z变换方法的优点，既能保持较好的吸收精度，又能保持较好的效率，而且可以方便、直接地离散Maxwell方程组.

1 PML算法推导

在三维SC-PML区域中，频域Maxwell旋度方程可以表示如下：

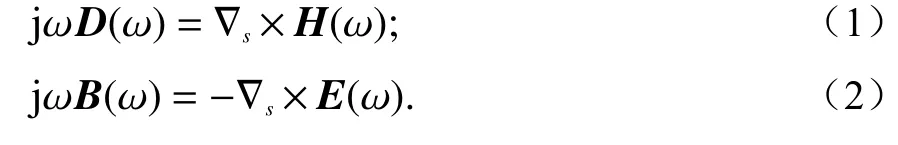
如式(1)与(2)所示，电通量D和磁通量B本构关系式可以被应用于更新电场与磁场，优点在于可以避免考虑材料的具体属性[31]，定义如下：

式中，εr(ω)和µr(ω)分别是FDTD计算域的相对介电常数和导磁率.

式(1)和(2)中的操作算子定义为

式中，Sη(η=x,y,z)是n阶复数拉伸坐标变量，且有

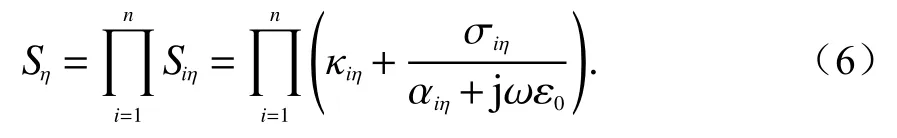
为了节省更多的内存，我们采用一阶CFS-PMLSη(η=x,y,z)，表达式为

式中：κη是大于等于1的实数；ση和αη均被假定为正实数. 接下来，重新对式(7)进行整理和简化，如下：

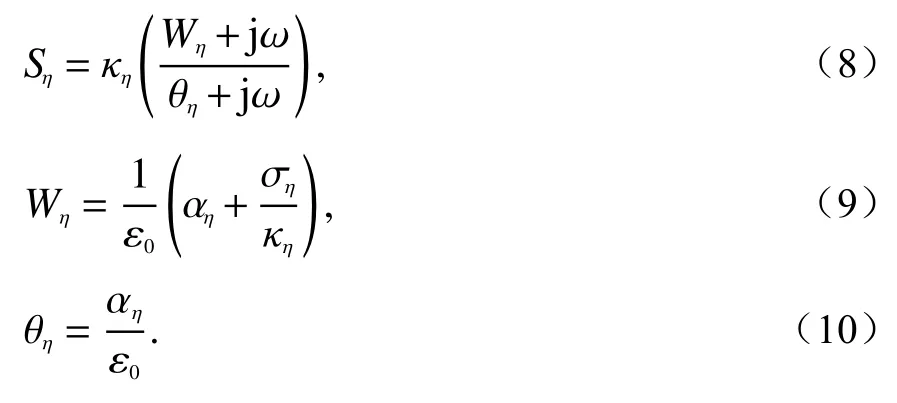
接着，将式(8)的倒数转换到s域，结合关系式jω→s, 采用如下BZT方法：

可以得到

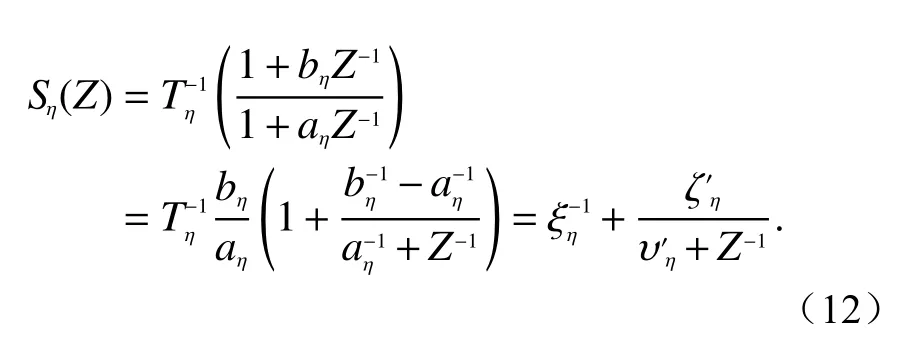
式中：至此，我们已经取得了复数拉伸变量的Z域表达式.

接下来，以x场分量为例，在笛卡尔坐标系下展开式(1)如下：

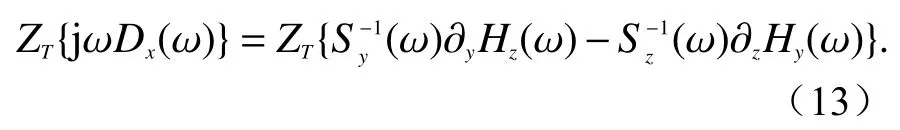
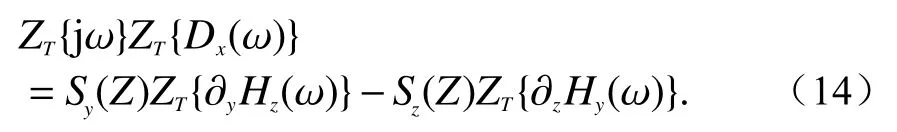
因此，在Z域中有

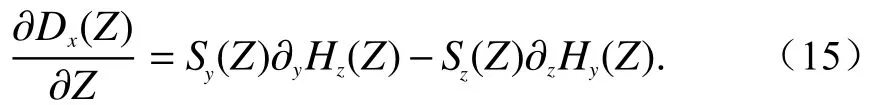
将式(12)代入式(15)，并引入辅助变量ψ，有

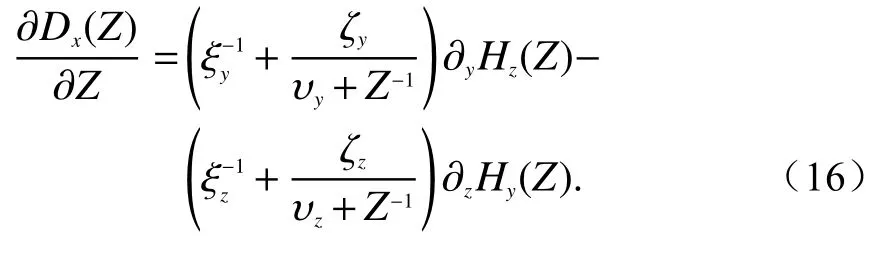
经过整理，我们得到：

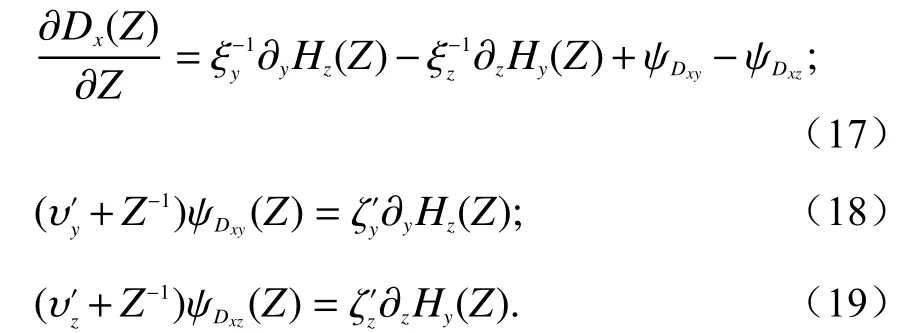
为了更加简易地采用ME方法[30,32]，需要进一步整理式(17)，并在式(18)和(19)等式左边添加ψDxy−ψDxz，然后再在两边乘以1/Δt，有：

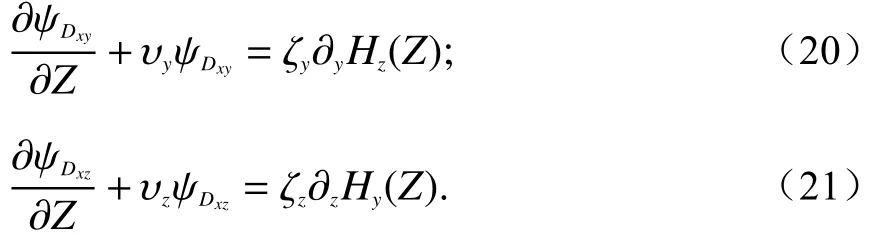
式中：

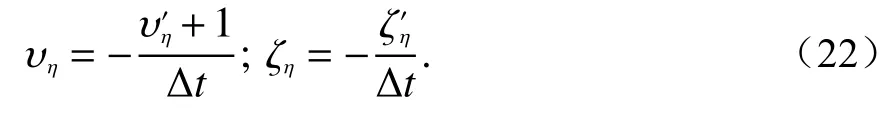
因此可以总结得到不同场量的表达通式为

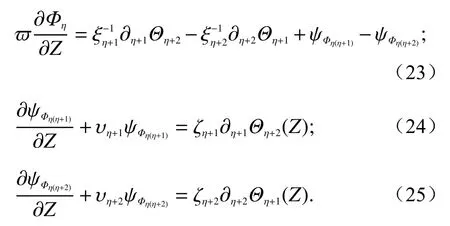
式中，Θ和Φ为FDTD迭代过程的电场和磁场的通用符号. 当Θ=E时Φ=H，当Θ=H时Φ=E，我们可以取得所有的矢量方程，如下式：

式中：

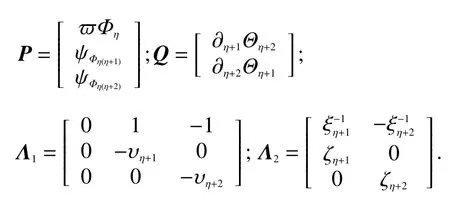
假定初始条件为t0，我们可以取得

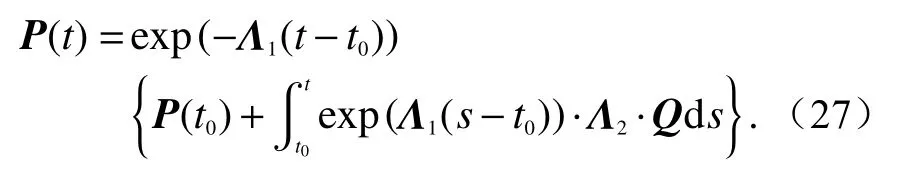
通过采用上一时间步nΔt取代t0，式(27)关于新的时间步(n+1)Δt可表达如下：

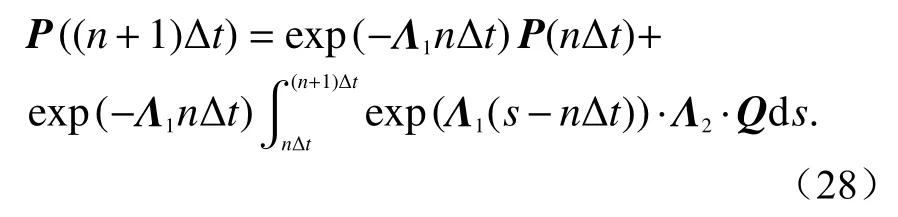
再次简化式(28)，有

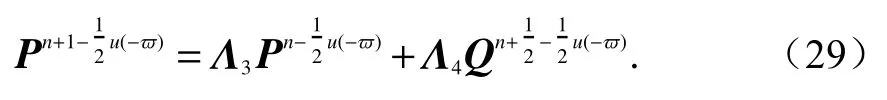
式中，

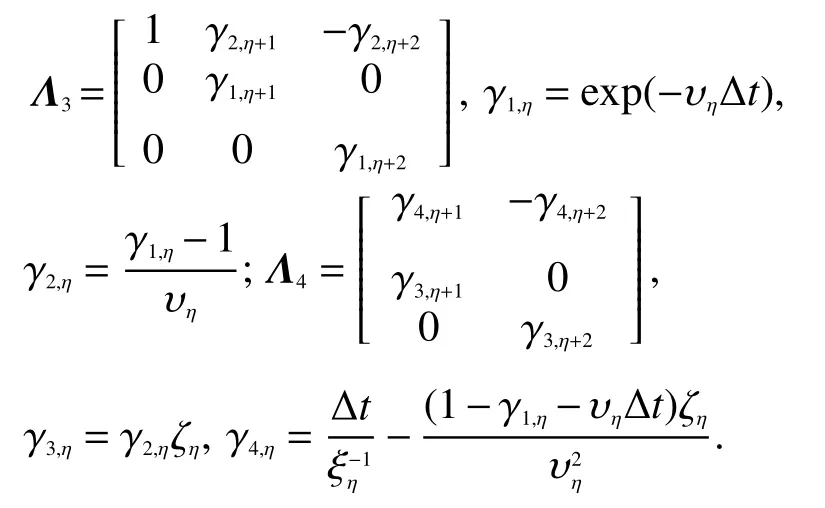
在FDTD计算中，在第nth时间步，PML区域的实现步骤如下：

第一步 边界预存储场

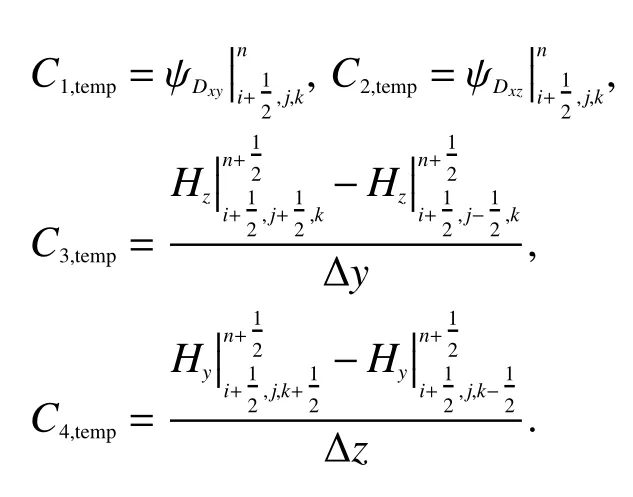
第二步 电通量场迭代(以x场分量为例)

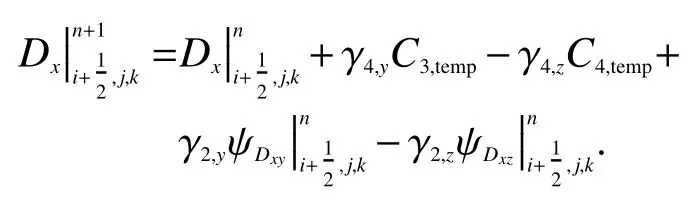
第三步 更新辅助变量

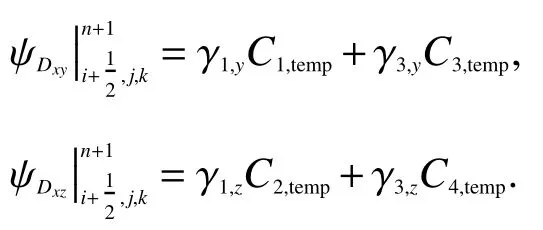
目前为止，我们已经推导得到了完整的数学表达式. 为了能够阐述所提出算法BZT-ME-PML的有效性和高效性，另外七种方法也被实现用以对比，分别是ME-PML、Conventional PML、DZT-PML、CPML、ADE-PML、BZT-PML，以及MZT-PML.

为了验证本文提出的方法在PML上的数值色散问题，在三维的数值色散关系中，必然满足

通过对正弦函数泰勒展开可以得到

考虑到一般网格在各坐标轴的方向上都取相同的厚度δ，即Δx= Δy= Δz=δ，cΔt= 0.5δ，此时

假定各方向的数值波长为λdη=λ0δ−1(η=x,y,z)，将式(32)中的高阶项消去可得

式中：

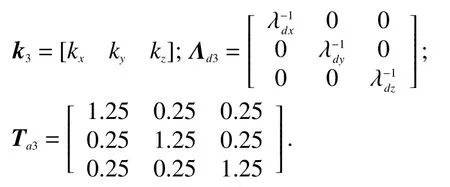
不妨令数值色散关系的特征矩阵为

发现在PML层中必然受到空间波矢(kx,ky,kz)的影响，在全局电磁空间的FDTD计算可以与矩阵K3构成数值精度上的正相关关系，在侧面上也验证了在PML-ABC层下的FDTD方法与无吸收边界的FDTD方法具有相同的数值色散关系. 因此，可以给出三维情形下的FDTD关于数值波长λdη(η=x,y,z)的评价函数为

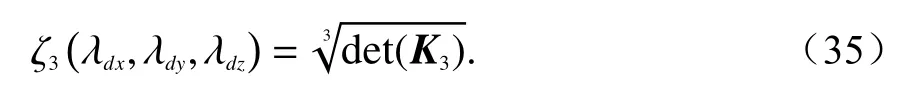
由此得到表1的列表.

表1 λdz = 25时FDTD评价函数ζ3 (λdx, λdy, 25)的取值Tab. 1 The numerical value of evaluation function ζ3 (λdx, λdy, 25) of FDTD at λdz = 25

当各方向的数值波长均大于25时，PML-ABC下的三维FDTD方法可以保持数值误差在2.867 6×10−3以下，也肯定了本文提出的PML算法能够有效收敛且计算稳定.

2 数值算例实验

2.1 TE极化电磁波与完纯导体片的相互作用问题

为了验证本文所提出算法的有效性，我们采用8G内存i7-8750H CPU的计算机进行算法验证. 首先仿真一个二维数值算例. 如图1所示，一个TE极化的电磁波与一个在z方向上无穷大而在x方向上有限长度的完纯导体片的相互作用，空间步长是Δx=Δy=1 mm，时间步长是Δt=1.178 5 ps ≈0.5×CFL ，其中CFL表示FDTD方法离散时间长度的稳定因子，一个宽度为100个元胞的PEC被自由空间所包围，10个元胞厚度的PML截断自由空间，在各个方向上PML与PEC的距离是3个元胞.

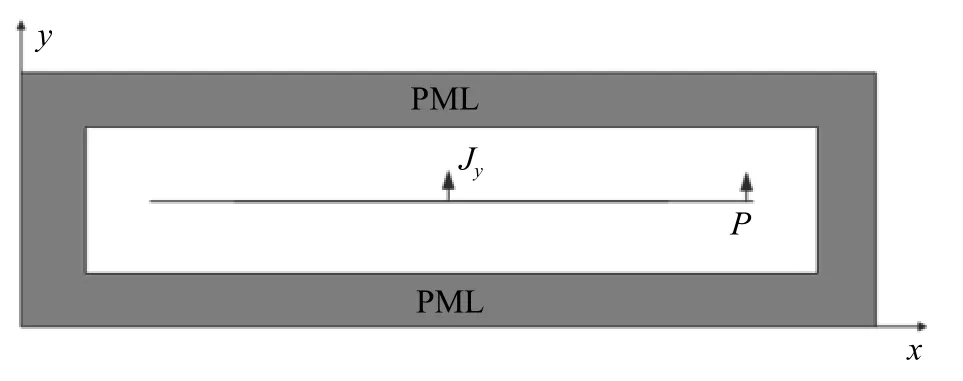
图1 二维仿真中的FDTD模型Fig. 1 The FDTD model in 2D simulation

一个在z方向上无穷长的y方向极化的线电流源被放置在中心，并且被一个微分高斯脉冲所激励[33-34]，其中tw=26.53 ps，t0=4tw. 观察点“P”选取在PEC薄片的边上. 参考解网格充分大以至于在1 500个时间步内没有来自外边界的反射波. PML参数设定如下：对于传统PML，κmax=9，σmax= 0.6σopt；对于CFS-PML，κmax= 10，σmax= 0.9σopt，αη= 0.05.

我们提出的方法与无吸收边界的传统FDTD进行对比得到的最大相对反射误差(maximum relative reflection error, MRRE)公式为

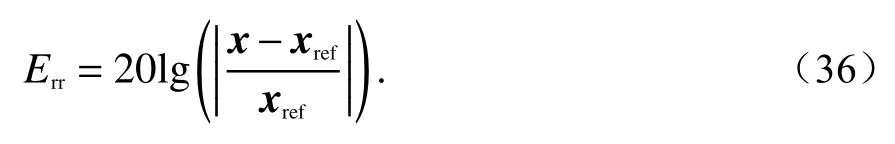
式中：x为我们提出的方法所获取到的场数据；xref为无吸收边界的传统FDTD的场数据.

相对反射误差(relative reflection error，RRE)曲线的计算结果如图2所示. 另外，对不同算法中的MRRE对应内存和计算时间(时间步=20 000)进行统计，结果如表2所示. 图2和表2表明，二维算例结果验证了所提算法的有效性. 从图2看出，所提出的算法比首次提出的基于辅助微分方程的ME-PML在吸收精度上有些许提高，比其他的PML方法在吸收精度上有明显提高.

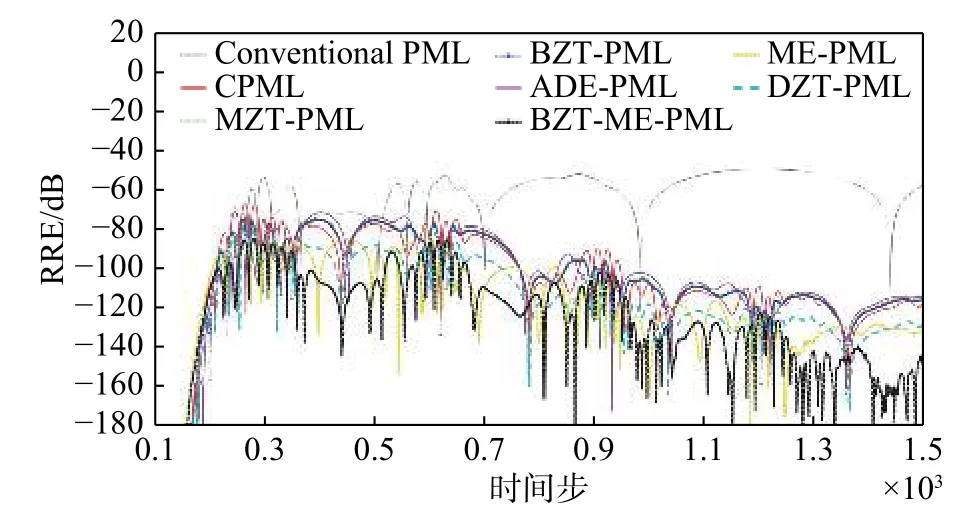
图2 二维FDTD情况下不同时间步数下的RRE曲线Fig. 2 The RRE curve under the different time steps in 2D FDTD cases

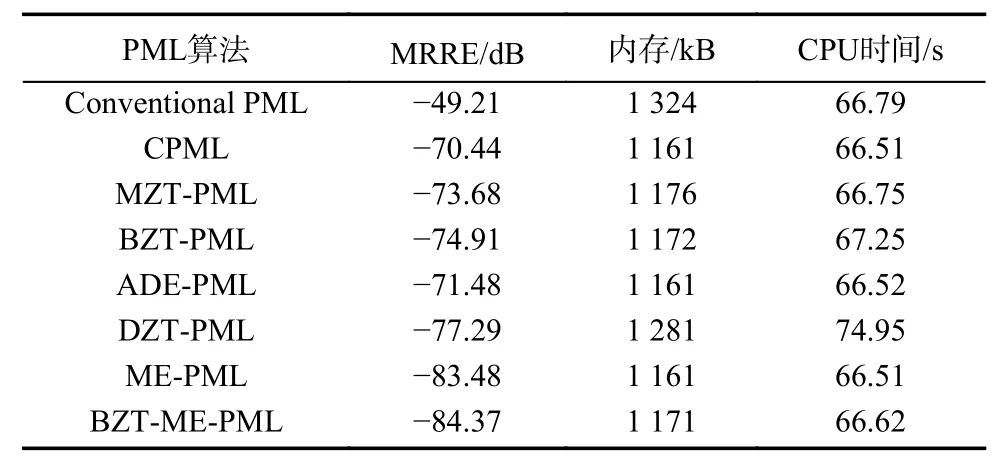
表2 二维FDTD情况下不同PML算法实现的性能对比Tab. 2 The computation comparison in those different PML methods in 2D FDTD cases

2.2 金属薄板嵌入在有耗电介质中的三维模型

为了进一步验证所提出算法的有效性，一个100 mm× 25 mm的金属薄板(被仿真为完纯导体)嵌入在本构参数为ε和σ的有耗电介质中的问题被采用[23]. 有耗电介质的本构参数被假设为εr=7.73和σ=0.273. 三维FDTD计算域(图3)是106× 31× 6，空间步长和时间步长分别是Δx=Δy=Δz=1 mm和Δt=5.3 ps. 在每个方向上再用厚度为10个元胞的PML去截断FDTD计算域. 在PML区域，ση和κη采用PML内部中本构参数分布，其中m=4；而αη是常数，即不会随着空间位置发生变化. 一个在垂直方向上极化的激励源Js被放置于金属薄板中的左上角，其中，tw=83 ps，t0=4tw. 观察点“P”放置于金属薄板的对角线上.

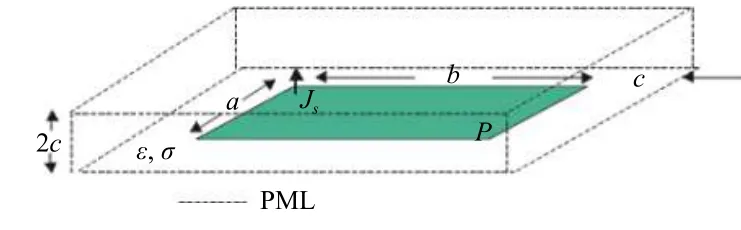
图3 三维仿真中的FDTD模型Fig. 3 The FDTD model in 3D simulation

PML参数设定如下：对于传统PML，κmax= 14，σmax= 0.56σopt；对于CFS-PML，κmax=11，σmax= 0.4σopt，αη= 0.05.

由图4和表3可知，在处理三维问题时，所提出的算法的有效性得以进一步验证.

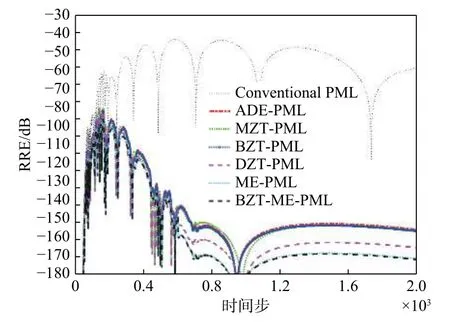
图4 三维FDTD情况下不同时间步数下的RRE曲线Fig. 4 The RRE curve under the different time steps in 3D FDTD cases

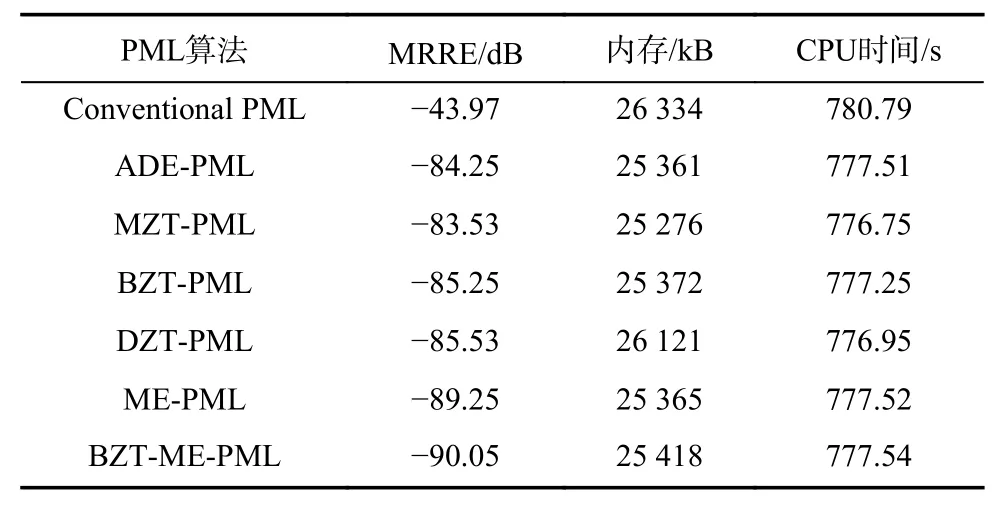
表3 三维FDTD情况下不同PML算法实现的性能对比Tab. 3 The computation comparison in those different PML methods in 3D FDTD cases

2.3 三维VLF地下探测问题

目前为止，二维和三维算例已经被用于验证所提出算法的有效性和稳定性. 接下来，为了进一步验证所提出算法的优势：高精度(ME技术)、易操作和粗空间网格设置(BZT变换)，两个三维VLF地下探测和一个三维VHF地下成像问题被采用.

众所周知，一个高效的ABC应该被使用截断带有高损耗媒质的FDTD计算区域，用以模拟开域空间问题，使得电磁波相互作用的解可以被精确计算.为此，一个三维色散半空间问题被实现，如图5所示，可以看到三个矿体分布在不同的内部区域.

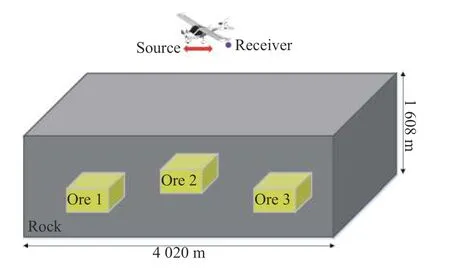
图5 三维情形下的内嵌立方矿体的半空间几何模型Fig. 5 The half-space geometry with three different cubic ores in 3-D cases

整个FDTD计算区域分别包含空气、围岩(电导率σrock=0.005 S/m)，以及矿体(电导率σore=4 S/m). 三个立方体矿体(大小为268 m× 268 m× 268 m)内嵌在岩石区域，且它们的几何中心位置坐标分别为(2 010, 1 608, 670) m、(2 010, 2 010, 804) m、(2 010, 2 412,670) m. 空间离散元胞大小为Δx= Δy= Δz= 67 m. 整个FDTD计算区域大小为4 020 m× 4 020 m×2 010 m. 激励源采用的是磁点偶极子源，位于(2 010,2 010, 1 742) m的空气中. 接收点位于(2 077, 2 077,1 809) m.如图6，一个频率为25 kHz的双极性方波脉冲被采用，是因为该激励是适合应用于航空瞬变电磁系统问题. 如图7所示，横坐标为0.16 ms的时间窗被用于展示所提出算法与其他算法在接收点处的吸收性能.

图6 频率为25 kHz的双极性方波脉冲(上升期是0.005 ～0.015 ms，下降期是0.025 ～ 0.035 ms)Fig. 6 Bipolar square wave pulse with frequency of 25 kHz(rising period at time = 0.005−0.015 ms, falling at time = 0.025−0.035 ms)

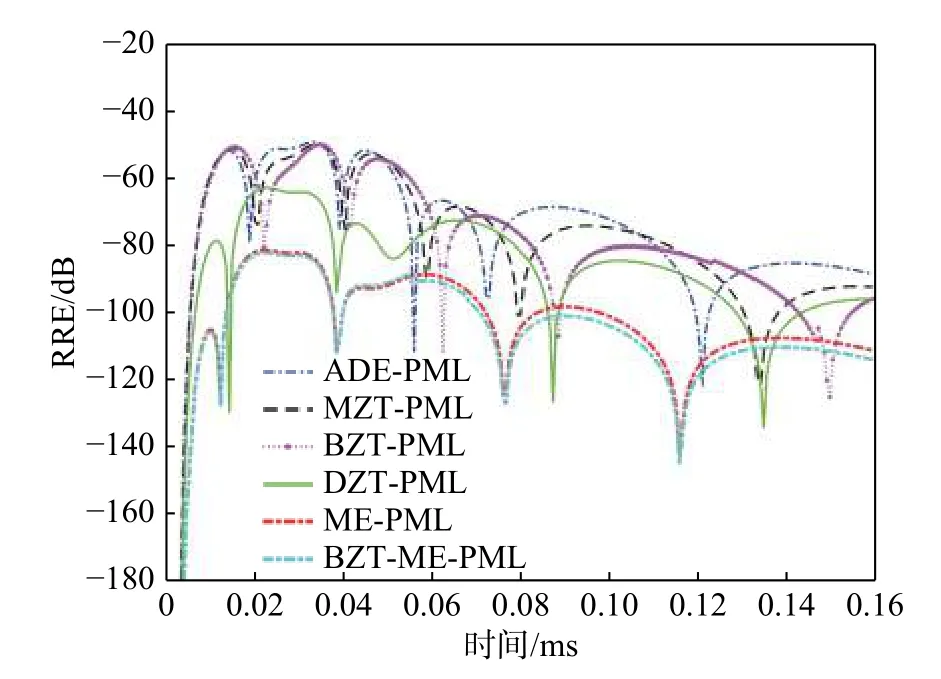
图7 在内嵌立方矿体的半空间几何模型下的RRE曲线Fig. 7 The RRE curves under the half-space geometry with three different cubic ores

为了观察比较MRRE，一个参考解需要被提供，即在原先计算模型的大小上向各个方向拓展100个元胞，最外层采用相同个数的PML截断计算区域.观察点处的MRRE可以通过式(30)计算得出.

由图7可知，所提出算法与其他算法的MRRE分别是ADE-PML (−49.19 dB)、MZT-PML (−49.74 dB)、BZT-PML (−49.98 dB)、DZT-PML (−62.90 dB)、MEPML (−81.29 dB)，以及BZT-ME-PML (−82.09 dB).

为了更加符合真实环境中不规则的地形分布，地面不规则模型被模拟，其中三个矿体也是不规则地分别内嵌在岩石层中，如图8所示，整个计算区域大小为4 020 m× 4 020 m× 2 010 m，而地下岩石的探测区域为1 608 m. 激励源采用的是电线源，坐落在岩石层表面，脉冲仍然是双极性方波脉冲. 空间元胞大小为Δx= Δy= Δz= 67 m.

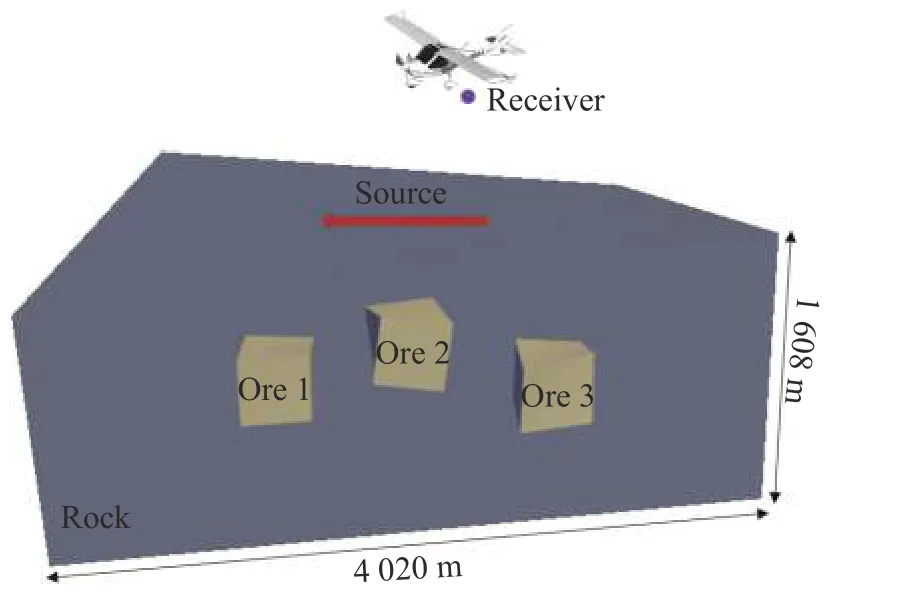
图8 三维情形下的不规则的半航空瞬变电磁几何模型Fig. 8 The electromagnetic geometry for irregular semiaeronautical transients in 3-D cases

采用同图7一样的时间窗进行观察，结果如图9所示. 可以看到，不同PML算法的MRRE分别是ADE-PML (−95.81 dB)、MZT-PML (−95.71 dB)、BZTPML (−95.16 dB)、DZT-PML (−109.2 dB)、ME-PML(−113.2 dB)、BZT-ME-PML (−114 dB).

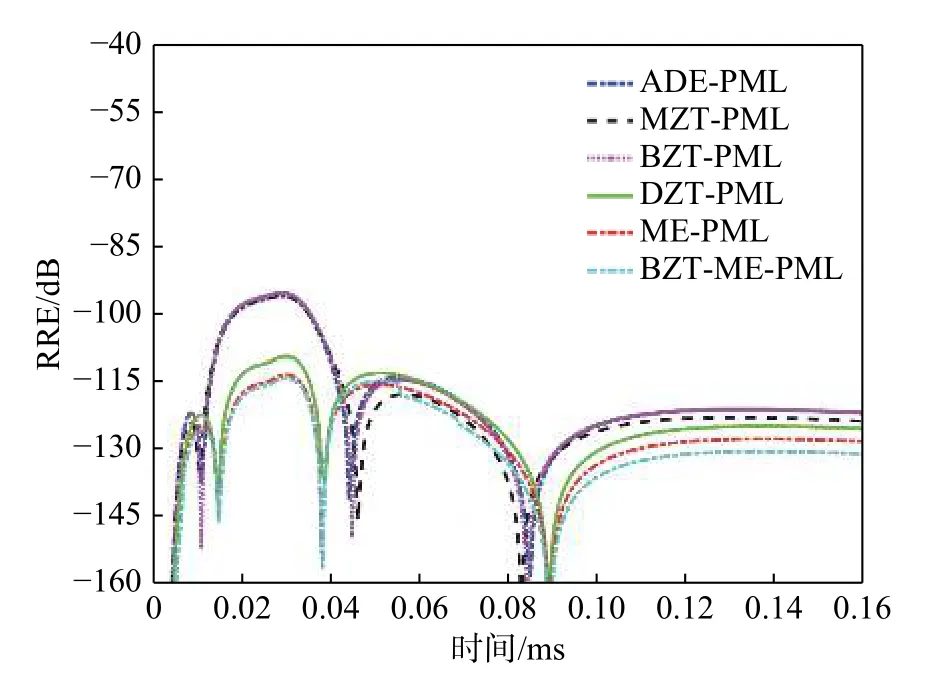
图9 在不规则半航空瞬变电磁几何模型下的RRE曲线Fig. 9 The RRE curves under the electromagnetic geometry for irregular semi-aeronautical transients

2.4 三维VHF地下成像问题

为表明所提出算法的鲁棒性和完整性，一个三维VHF地下成像问题被考虑. 据我们所知，嫦娥5号探测工程项目即将发射升空对月球表面进行探测，并在不久的将来采样回地球. 因此，在地球上进行高分辨率地下成像是非常有必要的. 在过去的研究中，月球表面土壤的相对介电常数默认为εr= 3[35-37]. 为了模拟月球环境，我们采用相对介电常数为εr= 3的火山灰替代月球表面土壤作为嵌入目标体的背景，以此在地球上进行月球探测的实测实验.

如图10所示，来自实测月球探测系统嫦娥五号的两个单站实验数据被提取，填充了火山灰的地下实验模型大小为2.5 m × 2.0 m × 1.0 m.

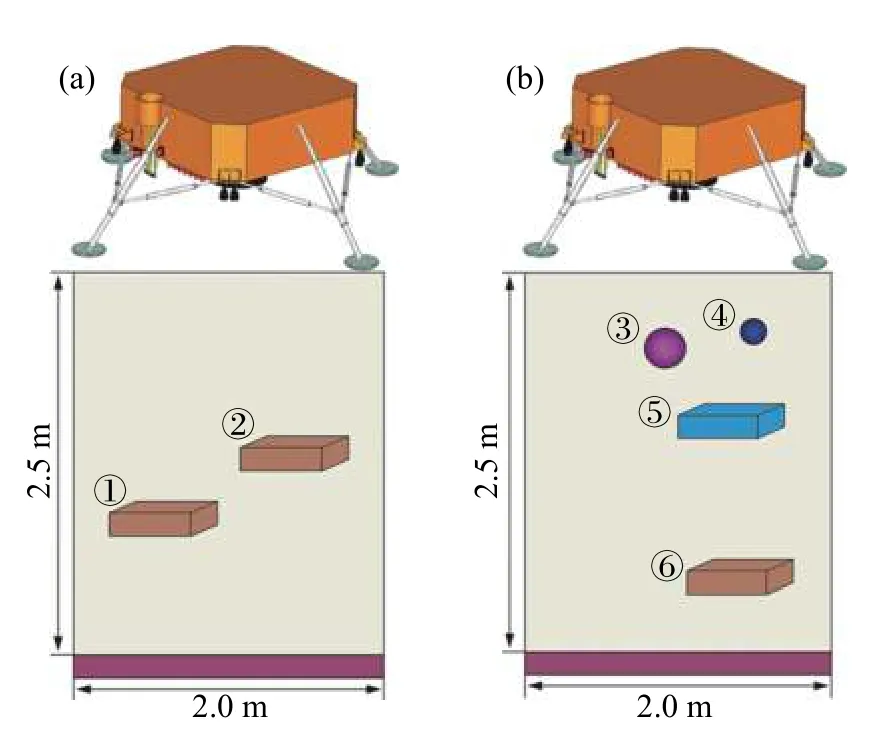
图10 嫦娥五号提供的两个单站实验室数据采集系统Fig. 10 The data-acquisition systems of two single station provided by Chang’e-5

在实测实验中，激励信号从嫦娥五号超宽带雷达系统中发射，并在多道天线中记录. 在嫦娥五号实测结束之后，所提出的BZT-ME-PML算法被应用于实现地下成像，如图11 所示. 因此，这也进一步证明了所提出算法的有效性和稳定性.

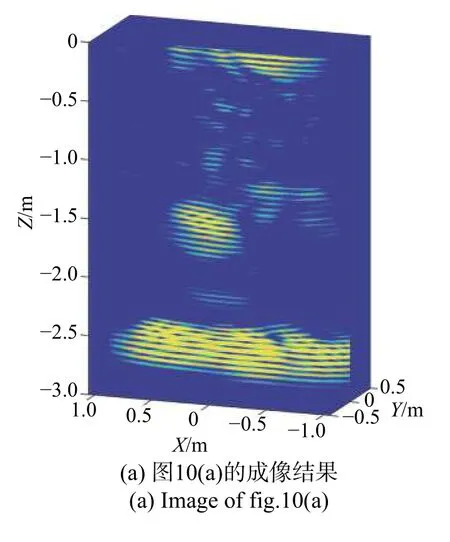
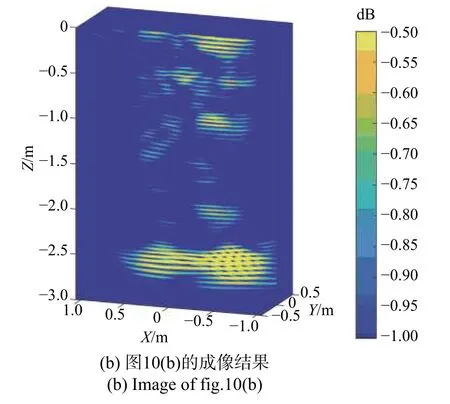
图11 嫦娥五号超宽带系统实测数据的逆时偏移成像结果Fig. 11 Reverse time migration imaging results of Chang’ E-5 UWB system measured data

3 结束语

利用ME方法，所提出的紧凑型BZT-ME-PML算法能够高效地求解VLF地下探测和VHF地下成像问题. 所提出的算法具有避免进行公式重整理、卷积操作和变量替换等优势，使得计算过程变得高效.此外，由于采用了BZT方法，无论是频域相乘还是时域卷积都可以对应到Z域相乘，使得所提出的算法具有易操作性. 因此，同时结合ME技术和Z变换方法，所提出的BZT-ME-PML算法不仅具有较好的吸收性能和高效率，而且易于直接离散Maxwell旋度方程. 最后，理论推导及算例表明该方法有效可行的.