几种抛物方程形式的相位误差分析

蒲玉蓉 王丹丹 席晓莉 刘江凡

（1. 西安理工大学自动化与信息工程学院，西安 710048；2. 山东科技大学电子信息工程学院，青岛 266590）

引 言

近年来，抛物方程(parabolic equation，PE)方法作为一种有效的数值计算方法，被广泛地应用于电波传播[1-8]和水声传播[9-10]等领域. PE是根据波的单向传播过程，对亥姆赫兹方程作近轴近似得到的一种抛物型偏微分方程形式，因此不同的近轴近似方式就得到不同的PE形式. 尽管相较于亥姆赫兹方程，PE的求解更为方便，但由于近轴近似的引入，使得PE存在自身固有的相位误差[10]. 该固有相位误差会导致PE方法所模拟的电/声波波数与传播方向相关，呈现出空间各向异性特性. 通常，电/声波传播仰角越小，仿真波数与真实波数越接近，即表现为近轴传播特性[1]. 多年来，为了减小PE的固有相位误差，以增加PE的计算仰角范围，学者们提出了一系列的PE形式，从早期的标准PE(standard PE, SPE)[11]和Tappert型PE[12]到后来的Feit-Fleck型PE[13]、Claerbout型PE[14]、Greene型PE[15]和Lin-Duda型PE[16]. 1978年，Feit等人提出近似误差限的思想[13]，用于比较SPE和Feit-Fleck型PE的精度，并表明Feit-Fleck型PE的精度明显优于SPE. 1983年，Thomson等人采用该近似误差限方法评估了水下声波传播环境中SPE、Tappert型PE和Feit-Fleck型PE的精度[17]，进一步验证了Feit-Fleck型PE的优越性，并表明Tappert型PE并没有明显改善SPE的精度. 随后，Clearbout提出了一种更为严谨的色散分析方法[18]，用于研究水下声波传播环境中PE的精度，但是该方法并没有引起学者们的关注. 直到2020年，我们将该色散分析方法推广到起伏地形移位映像PE(shiftmap PE, SMPE)的相位误差分析中[19]，并得出与传统认知不同的结论，即Feit-Fleck型SMPE精度并非总是优于标准SMPE.

本文将进一步采用色散分析方法，评估现有的六种PE形式在对流层电波传播、水下声波传播和森林电波传播三种典型应用场景中的相位误差特性.首先，推导了各PE形式的色散关系；然后，基于色散关系，评估出三种典型场景中折射率与传播仰角对各PE形式相位误差特性的影响；最后，通过相位误差分析，得出各PE形式的精度，并给出固定相位误差限下各PE形式的适用仰角范围.

1 几种典型的PE形式

由于水下声波传播和电波传播所满足的PE形式完全相同，为了简化，这里仅从电波满足的二维标量波动方程出发推导几种典型PE的形式. 在直角坐标系中，设ψ表示矢量场的任一直角坐标分量，且满足ψ与y无关，则ψ满足二维标量波动方程

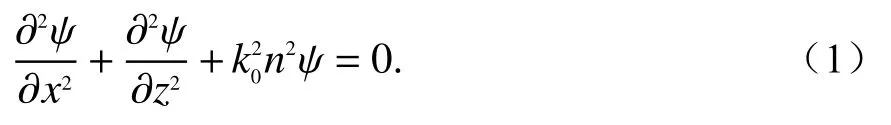
式中：k0为真空中的波数；n为媒质的折射率.

根据文献[20]，假设在电磁场传播过程中，折射率n几乎不随x变换，则可将式(1)分解为

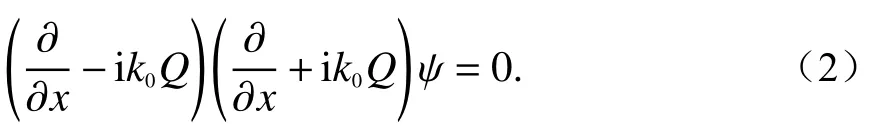
定义沿x轴正向传播的波函数为[20]

将式(4)代入式(3)中，可得前向傍轴波动方程为[1,20]

为方便数值计算，需对Q作近似处理. 对Q作不同形式的近似，使式(5)简化为不同形式的PE. 但同时，近似处理的引入会导致PE存在自身固有的相位误差，即表现出明显的近轴传播特性. 下面，介绍六种典型的PE形式：

1)SPE(也称Taylor型PE)[11]，其通过对Q取一阶Taylor展开得到.

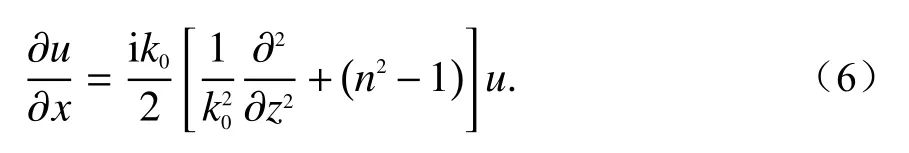
2)Tappert型PE[12]，由Tappert提出不久后又放弃的一种PE形式.

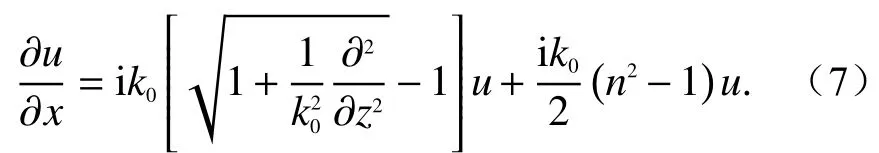
3)Feit-Fleck型PE[13]，由Feit和Fleck提出，并用于研究光纤中的电波传播问题.

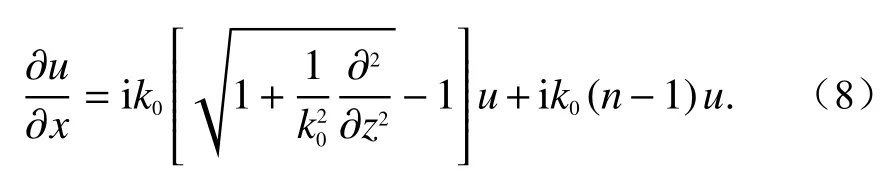
4)Padé型PE[14]，最早由Claerbout在研究地球物理问题时提出.

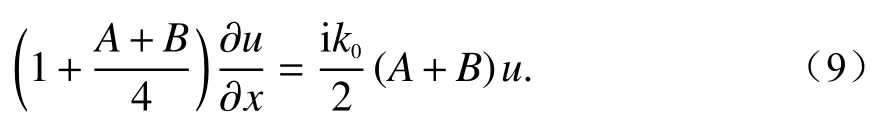
5)Greene型PE[15]，是Greene在研究水下声波、电波传播问题时，通过对Padé型PE优化系数而得到的.

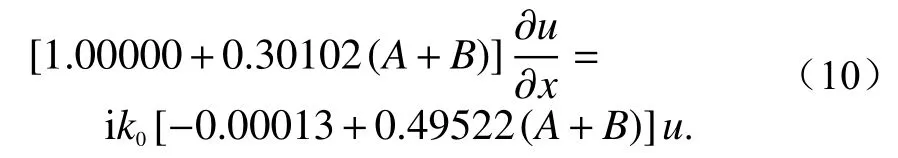
6)Lin-Duda型PE[16]，由Lin和Duda提出用于水声学传播问题的一种高阶PE.

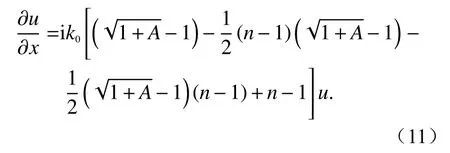
2 各PE形式的色散关系

色散分析方法的基本思想是将任意单位平面波解代入到PE中推导出色散关系，然后量化评估色散关系中每个因素与传播波数之间的关系. 忽略初始条件和边界条件的影响，式(1)所描述的齐次波动方程的单色平面波解可表示为

式中，θ为平面波的传播方向角. 将式(12)代入式(4)中，可得

接着，将式(13)代入式(5)中，可得

式(14)对应于均匀媒质中解析方法的色散关系，其表明，对于均匀媒质，前向傍轴波动方程不存在相位误差. 使得PE表现出近轴传播特性的原因是源于对伪微分算子Q的近似处理，下面将通过PE的色散特性来具体说明. 为此，首先推导PE所满足的色散关系.

根据式(13)形式，可假设PE所描述的平面波解为

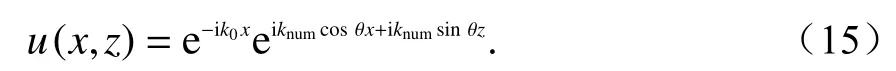
式中，knum为数值波数. 将式(15)分别代入式(6)～(11)，可依次得到：

1)SPE的色散关系

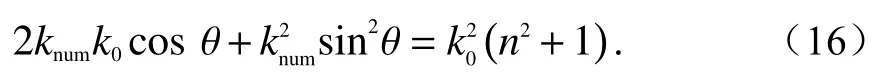
2)Tappert型PE的色散关系

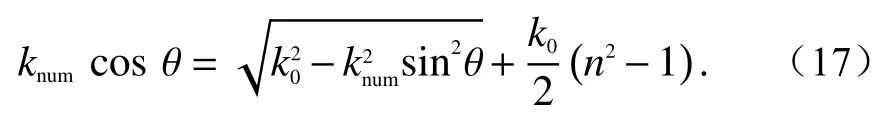
3)Feit-Fleck型PE的色散关系

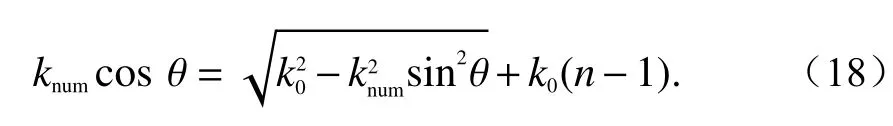
4)Padé型PE的色散关系

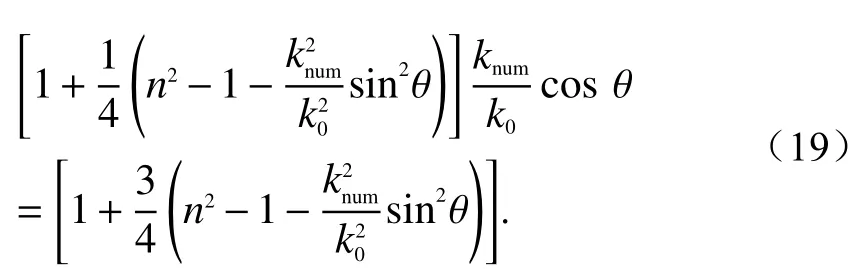
5)Greene型PE的色散关系

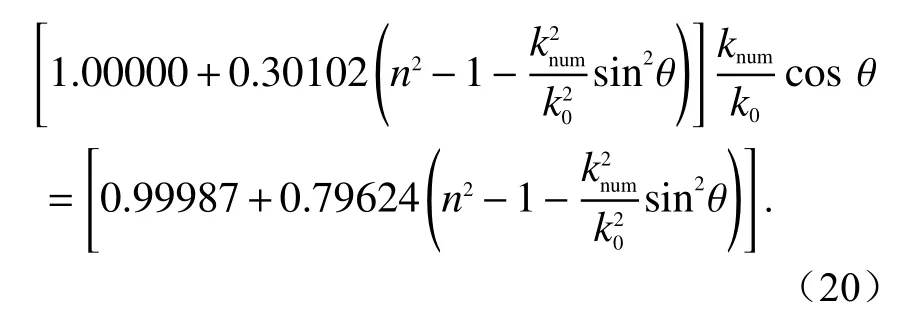
6)Lin-Duda型PE的色散关系

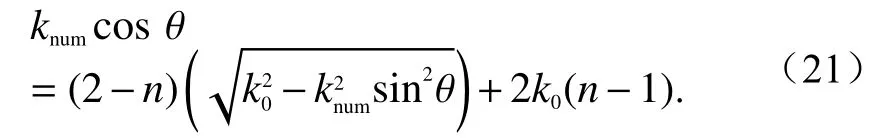
式(16) ～(21)表明，在各PE形式的色散关系中，数值波数knum同时与折射率n和传播方向θ相关. 这种非物理的色散现象必然会使得PE存在自身固有的相位误差，从而导致PE方法所模拟的电磁波波数与传播方向相关，呈现出空间各向异性特性. 并且，通常电磁波传播仰角越小，仿真波数与真实波数越接近，即表现为近轴传播特性.

3 相位误差分析

PE的色散关系给出了平面波的数值波数knum与折射率n和传播方向θ之间的关系，由此关系出发，可定量评估出这些因素对相位误差的影响，从而分析出各PE形式的精度. 定义相位误差函数为[19]

在常用的对流层电波传播、水下声波传播和森林电波传播场景中，三者折射率n的取值范围存在较大差异，并且水下声波传播中的波速度c也与其他两个电波传播场景不同，因此会使得三种场景中PE形式的相位误差特性存在差异. 目前在说明PE形式的精度时，经常会将多种应用场景中不同PE形式的分析结果放在一起讨论，这种做法缺乏合理性. 因此，下面将系统分析三种典型应用场景中，各PE形式的相位误差特性，以及各PE形式的计算仰角范围.

3.1 对流层电波传播场景

对于对流层电波传播环境，真空中的波速为2.997 924 58×108m/s，折射率n的上限取为1.001，其已远远超过地表观测到的大气折射率最大值，可以充分描述折射率的大小变化情况[1]. 图1给出了折射率n=1.0、1.000 1和1.001时，各PE形式的相位误差随传播仰角θ的变化曲线.

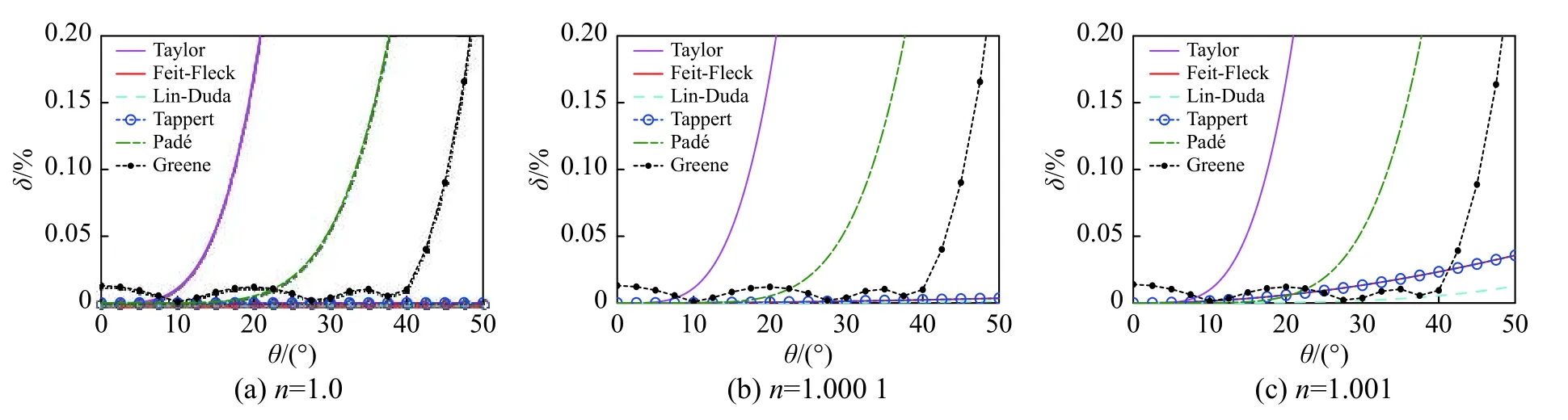
图1 对流层电波传播场景中不同折射率n时各PE形式的相位误差随传播仰角的变化曲线Fig. 1 Phase error as a function of the propagation angle for different refractive index n in tropospheric electromagnetic wave propagation scenario

由图1可以看出，SPE(即Taylor型PE)和Padé型PE的相位误差均随着传播仰角θ的增大而增大，且几乎不随折射率n变化；Greene型PE优化了Padé型PE中的系数，使得其相位误差约在40°以内的传播仰角都保持在较低的水平，且同样不受折射率n变化影响；Feit-Fleck型PE、Tappert型PE和Lin-Duda型PE均在n=1.0时，不存在伪微分算子Q的近似，即没有相位误差，而随着折射率n的增大，相位误差逐渐增大，并随传播仰角θ呈现出明显的空间各向异性特性. 进一步地由图1可得，对于均匀大气环境，Lin-Duda型PE是六种PE形式中精度最高的，而SPE是精度最低的；Feit-Fleck型PE和Tappert型PE的精度几乎完全相同，且高于Padé型PE，这与传统的近似误差限方法分析结论不同；通过对Padé型PE系数的优化，Greene型PE的全局误差明显低于Padé型PE. 此外，需说明的是Greene型PE的提出，为研究高传播仰角PE提供了新思路，其通过优化现有PE的系数，使得一定仰角范围内的全局相位误差最优，并且针对某些特定的电波传播问题，可使得目标传播角度范围内的相位误差最小.

为了更为直观地给出各PE的适用性，图2给出了各PE形式的相位误差与折射率n和传播仰角θ关系的等值线图. 由图2可知，各PE形式的适用仰角范围与其相位误差密切相关. 对于任意的折射率n，当相位误差限固定为0.02%时，SPE、Feit-Fleck型PE、Tappert型PE、Padé型PE和Greene型PE的适用传播仰角分别可达12°、37°、37°、25°和41°左右，而Lin-Duda型PE的适用传播仰角可大于50°.

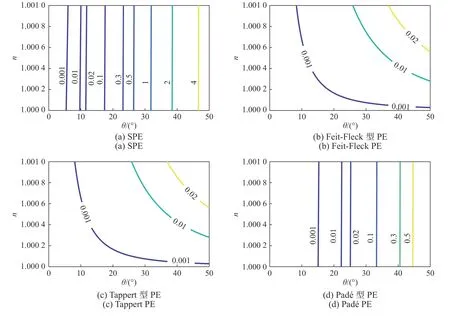
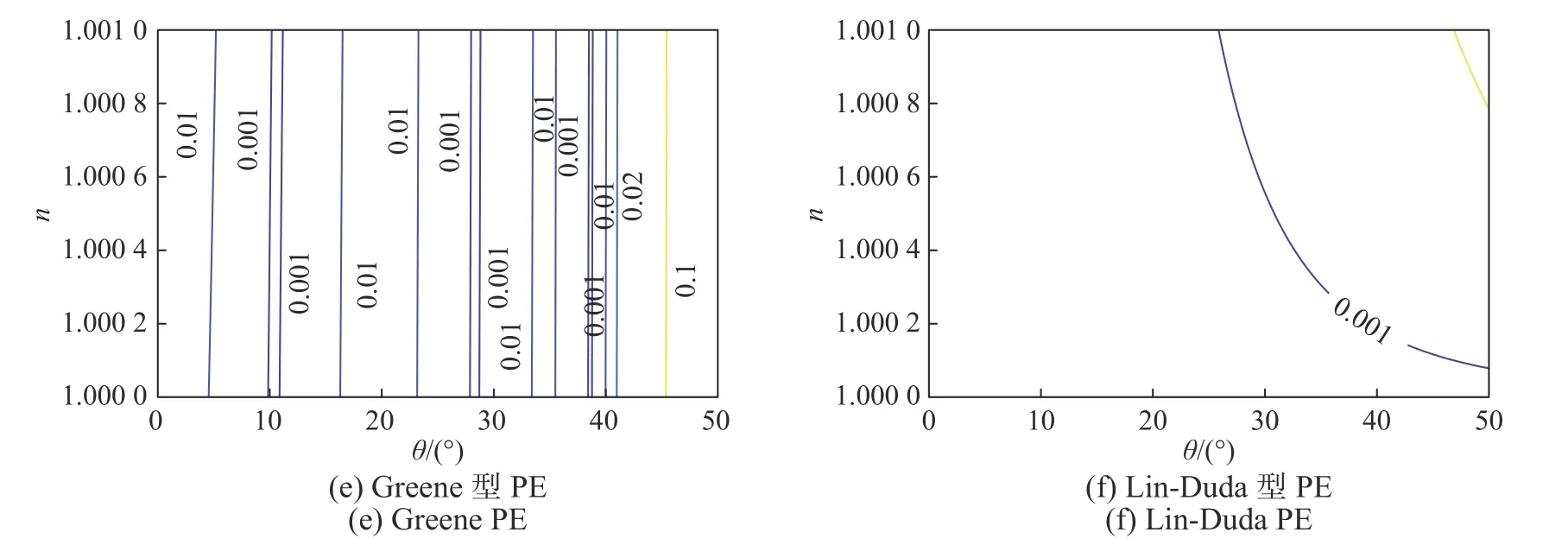
图2 对流层电波传播场景中各PE形式的相位误差随传播仰角/折射率变化的等值线图Fig. 2 The phase error as a function of the propagation angle/ terrain slope as a contour map for each PE form in tropospheric electromagnetic wave propagation scenario

3.2 水下声波传播场景

对于水下声波传播场景，通常将折射率n上限取为1.1，其远大于海洋环境中观测到的典型折射率值，水中声速取参考值1 500 m/s[17]. 图3给出了折射率n=1.0、1.01和1.1时各PE形式的相位误差随传播仰角θ的变化曲线. 由图3可以看出，水下声波传播场景中PE的相位误差特性比对流层电波传播场景中的更为复杂. 此时，各PE形式的相位误差特性同时与折射率n和传播仰角θ密切相关，其中：SPE、Tappert型PE和Greene型PE随着折射率n的增加，其相位误差极小值点由低传播仰角向高传播仰角偏移；Feit-Fleck型PE和Lin-Duda型PE在n=1.0时为解析形式，而在n大于1.0时，其相位误差同时随着传播仰角和折射率的增加而增加；Padé型PE的相位误差特性较为特殊，随着折射率n的增大，其相位误差总体减小. 进一步从图3可得：总的来说，对于水下声波传播场景，Padé型PE和Lin-Duda型PE的适用性是最好的；尽管Greene型PE全局误差总体较低，但是在折射率较大时，其目标仰角范围发生了偏移，这与其优化时所选取的折射率和仰角范围需求相关；由于SPE、Tappert型PE及Feit-Fleck型PE的精度对折射率的依赖性很强，致使其在水下声波传播场景的适用性受限，尤其是SPE和Tappert型PE，当折射率增大时，整体相位误差明显变大，且目标传播仰角范围向较高的传播仰角偏移.

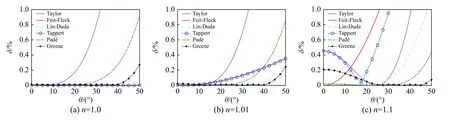
图3 水下声波传播场景中不同折射率n时各PE形式的相位误差随传播仰角的变化曲线Fig. 3 Phase error as a function of the propagation angle for different refractive index n in underwater acoustic propagation scenario

同样地，为了更直观描述各PE的相位误差与传播仰角θ和折射率n的关系，图4给出了三者之间关系的等值线图. 由图4可见，各PE形式的相位误差随传播仰角和折射率呈现出更为复杂的空间各向异性特性. 对于任意的折射率n，若相位误差限同样固定为0.02%时，由于目标传播仰角范围的偏移，SPE、Tappert型PE以 及Greene型PE均 不 适 用；Feit-Fleck型PE、Padé型PE以及Lin-Duda型PE的适用传播仰角分别可达3°、25°和23°左右.

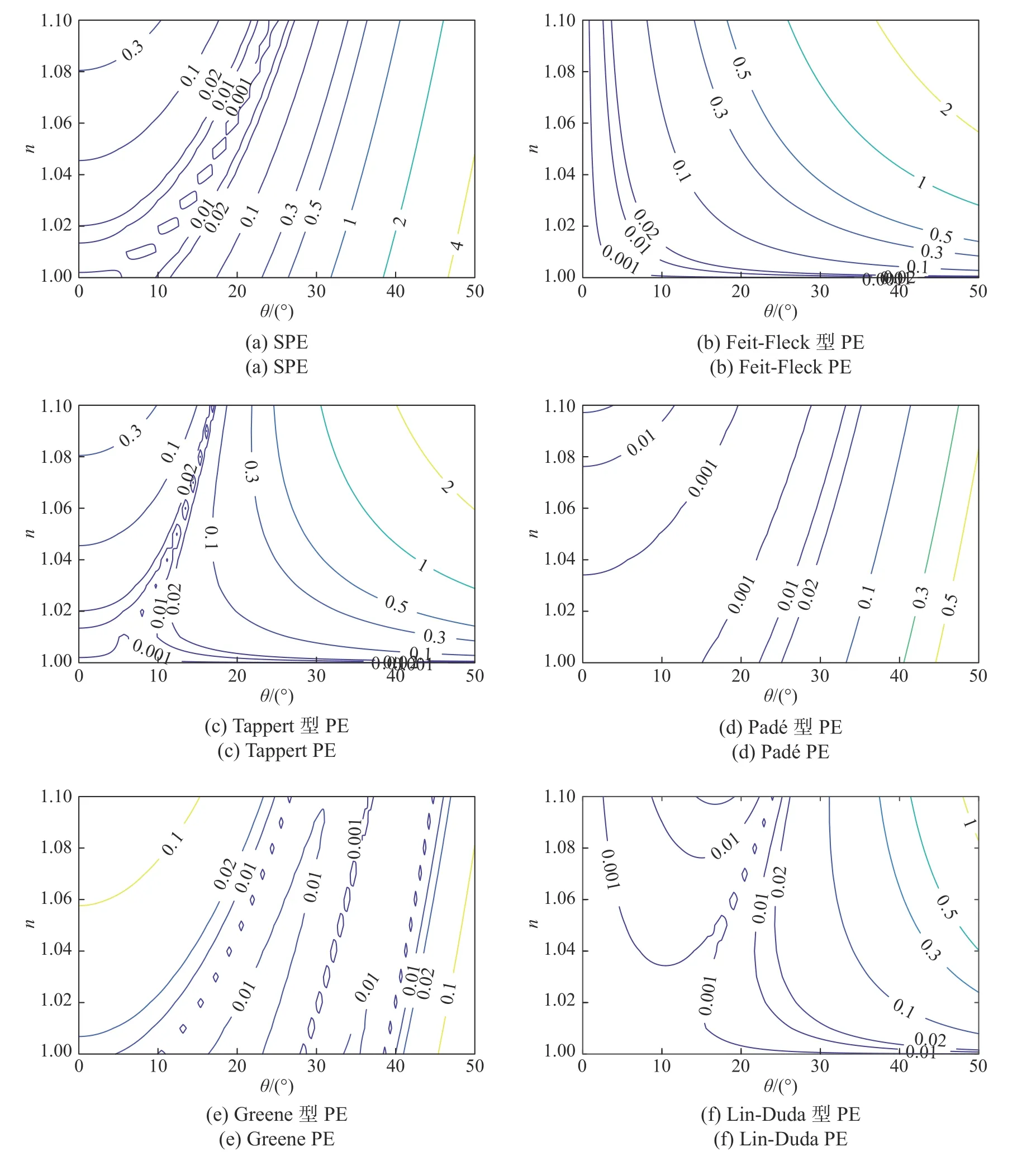
图4 水下声波传播场景中各PE形式的相位误差随传播仰角/折射率变化的等值线图Fig. 4 The phase error as a function of the propagation angle/ terrain slope as a contour map for each PE form in underwater acoustic propagation scenario

需要指出的是，目前各PE形式的精度比较结论多来自于水声学研究，且假定近似误差一定是随着折射率n的增大而增大，因此，一般取在n=1.1时分析各PE形式的精度，并得出：Padé型PE精度最高[1]，Feit-Fleck型PE精度高于SPE和Tappert型PE，且Tappert型PE没有明显改善SPE的精度[17]. 然而，由于PE的相位误差随着折射率n的增加并非单调递增变化，因此该分析结论存在自身局限性.

3.3 森林电波传播场景

相较于对流层电波传播场景和水下声波传播场景，森林电波传播场景往往更为复杂. 通常，PE方法在森林环境中应用时，是将森林植被对电波传播的影响等效到折射率n中考虑的，且不同于其他两种典型应用场景，森林场景中等效折射率n2变化范围往往更大，从1.01+0.01i到1.5+0.6i[8]，且通常为复数形式. 图5给出了等效折射率n2=1.01+0.01i、1.25+0.3i和1.5+0.6i时，各PE形式的相位误差随传播仰角θ的变化曲线.

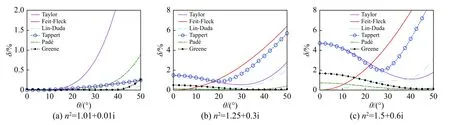
图5 森林电波传播场景中不同等效折射率n2时各PE形式的相位误差随传播仰角的变化曲线Fig. 5 Phase error as a function of the propagation angle for different effective refractive index n2 in forest electromagnetic wave propagation scenario

由图5可以看出：Feit-Fleck型PE和Lin-Duda型PE的相位误差同时随着传播仰角和折射率的增加而增加，即对于任意的等效折射率n，这两种PE形式适用于低仰角问题；SPE、Tappert型PE、Padé型PE和Greene型PE均随着折射率n的增加，出现相位误差极小值点向高传播仰角偏移现象，即适用目标传播仰角偏移问题. 进一步由图5可得，对于森林电波传播环境，Lin-Duda型PE的精度相对来说是最高的，但该PE形式也仅仅对于等效折射率较小的情况有效，而在等效折射率较大的情况下，适用性明显受限.

同样地，为了更为直观地分析各PE的适用性，图6给出了各PE形式的相位误差与折射率n和传播仰角θ关系的等值线图. 这里对等效折射率n2从1.01+0.01i到1.5+0.6i均匀采用，由于复数n2是一个二维概念，无法在单一坐标轴呈现复折射率，因此图6中采用折射率n的实部来表示复折射率n. 由图6可见，与前两种电波传播场景相比，森林电波传播场景中各PE形式的相位误差明显更大，适用角度范围明显减小. 这是由于森林场景中等效折射率n的取值通常比其他两种场景更大，且存在虚部导致的. 对于任意的等效折射率n，若相位误差限同样固定为0.02%时，SPE、Tappert型PE以及Padé型PE及Greene型PE均不适用；Feit-Fleck型PE和Lin-Duda型PE的适用传播仰角分别可达2°和4°左右.

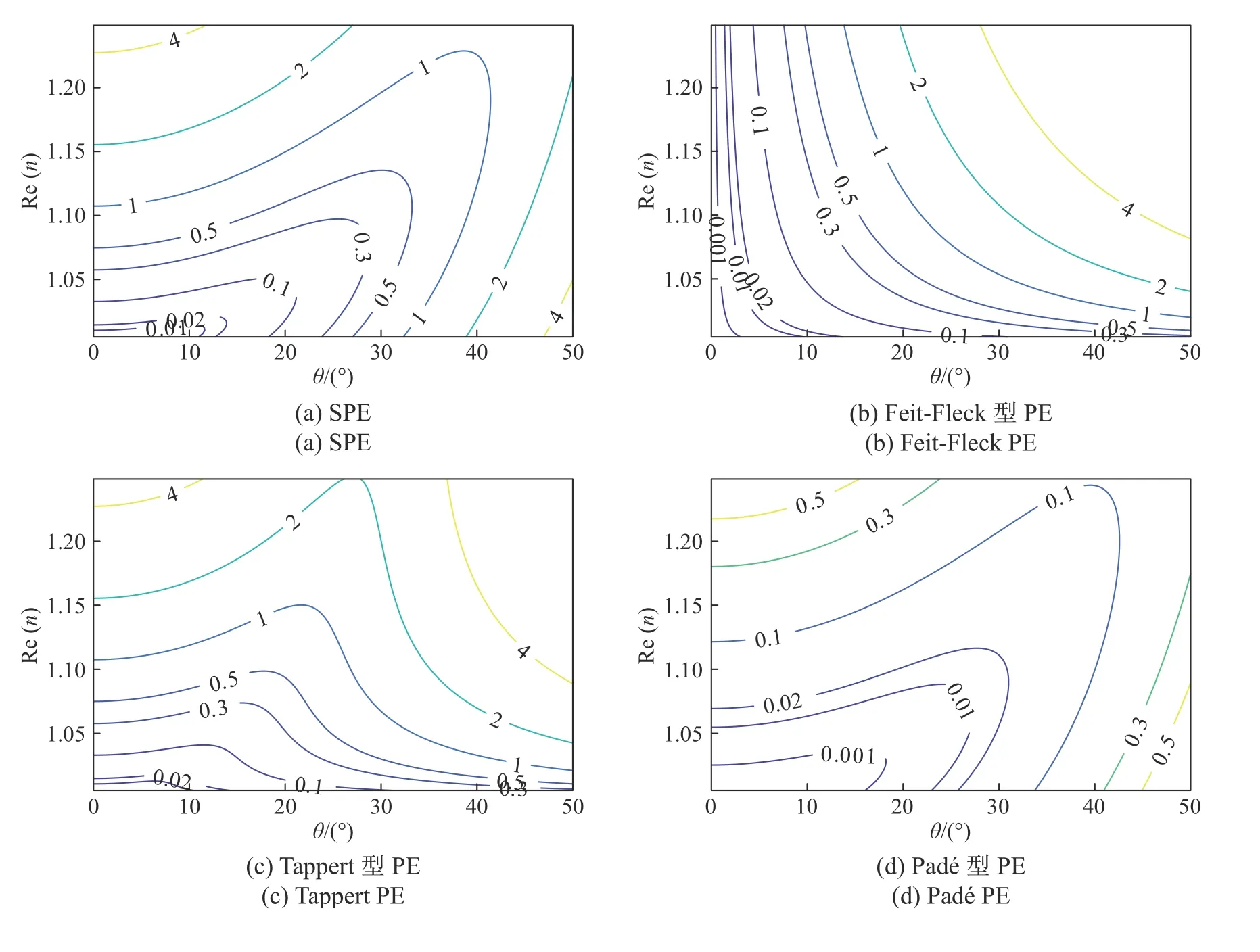
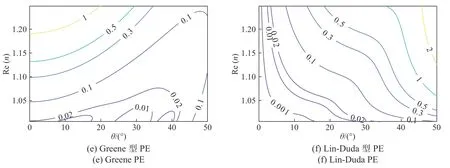
图6 森林电波传播场景中各PE形式的相位误差随传播仰角/折射率变化的等值线图Fig. 6 The phase error as a function of the propagation angle/ terrain slope as a contour map for each PE form in forest electromagnetic wave propagation scenario

4 结 论

本文采用色散分析方法，通过研究现有六种PE的相位误差特性，分析出对流层电波传播、水下声波传播和森林电波传播三种典型场景中各PE形式的精度. 研究表明：对于对流层电波传播场景，Lin-Duda型PE的精度最高，而SPE的精度最低；Feit-Fleck型PE和Tappert型PE的精度几乎完全相同，且高于Padé型PE；系数优化的Greene型PE全局误差明显低于Padé型PE. 对于水下声波传播场景，Padé型PE和Lin-Duda型PE最 为 准 确；Greene型PE全局误差较低，但在较大折射率时，存在目标传播仰角偏移现象；Feit-Fleck型PE、Tappert型PE和SPE型PE在此场景的精度都很有限. 对于森林电波传播场景，Lin-Duda型PE的精度依旧是最高的，但也仅对折射率较小的情况有效.

进一步地，通过固定相位误差限给出了三种场景中各PE形式的适用仰角范围. 对于对流层电波传播场景，SPE、Feit-Fleck型PE、Tappert型PE、Padé型PE和Greene型PE的适用传播仰角分别可达12°、37°、37°、25°和41°左右，而Lin-Duda型PE的适用传播仰角可大于50°. 对于水下声波应用场景，Feit-Fleck型PE、Padé型PE及Lin-Duda型PE的适用传播仰角分别可达3°、25°和23°左右，而SPE型PE、Tappert型PE以及Greene型PE均不太适用. 对于森林电波应用场景，各PE形式的适用性均受限，最高精度的Lin-Duda型PE的适用传播仰角仅为4°左右. 本文的研究可为选取适合目标场景中的最优PE形式提供理论依据.