基于深度学习的全球电离层TEC预测

张富彬 周晨 王成 赵家奇 刘祎 夏国臻 赵正予

（1. 武汉大学电离层实验室，武汉 430072；2. 北京航空航天大学前沿科学技术创新研究院，北京 100191；3. 哈尔滨工业大学（深圳）空间科学与应用技术研究院，深圳 518055）

引 言

电离层总电子含量(total electron content，TEC)是电离层研究过程中的一个非常重要的参数[1]. 从理论研究意义上来说，分析电离层的活动以及电离层的不同时空尺度的变化规律，包括电离层的逐日变化、电离层扰动等现象，这些研究都可以基于TEC参数的获取和研究[2]；从应用角度来看，TEC的建模和预报对于卫星定位、导航、测控、时频传递等星地链路电波传播有着至关重要的意义[3-4].

电离层TEC的建模研究最早采用的是经验模型方法. Rawer等人首次提出了国际电离层参考(international reference ionosphere，IRI)模型，它是统计预报模型[5]，被空间研究委员会(Committee on Space Research,COSPAR)和国际无线电科学联盟(International Union of Radio Science, URSI)共同主导，而且此项目一直在不断更新. 由于众多学者的共同努力和新的建模技术的使用，IRI模型已经得到了很大的完善和改进[6-7]. 2015年，Aa等人提出使用卡尔曼滤波的数据同化算法对中国及其邻近地区的TEC进行建模，极大地改进了经验模型的预报效果[8].

人工神经网络的出现，为TEC建模提供了新的研究方向. 人工神经网络能够学习不同变量之间的复杂性，通过大量的神经元把输入的向量与输出结果建立函数映射关系. 正是因为这个特性，神经网络逐渐地被应用到电离层TEC的建模中[9-11]. 1997年，Cander等人开始利用神经网络来分析预测非线性时间序列，使用多层感知机的方法对不同电离层参数进行建模[12]. 2011年，Habarulema等人针对南非地区的电离层TEC建模，提出了一个基于神经网络的预测模型，该模型具有一个输入层、两个隐含层和一个输出层[13]. 2018年，Song等人提出一种遗传算法改进的神经网络进行中国区域TEC的预测，它克服了传统神经网络容易陷入局部最优的问题，预测误差在5～8 TECU左右[14]. 2020年，Cesaroni等人使用神经网络的方法对全球范围内不同地理位置的台站TEC进行预测，误差在3～5 TECU左右[15].

深度学习是一种特定类型的机器学习，它是在传统人工神经网络基础上的升级，可以使用训练网络自动提取数据的特征. 它的网络层数相比传统的神经网络更多，从理论上可以实现任意函数的拟合.2017年，Sun等人采用长短时记忆(long short-term memory, LSTM)网络的方法对北京地区的TEC进行预测，误差在3～4 TECU左右[16]. 2019年，Chen等人将深度卷积生成对抗网络(deep convolutional generative adversarial networks, DCGAN)应用到空间物理领域的TEC图片补全，通过添加一个额外的判决器以及使用IGS (International GNSS Service)提供的TEC地图作为先验知识，提出了一种基于正则化的DCGAN[17]. 文献[18]对电离层TEC预测的滑动平均自相关法、LSTM以及encode-to-decode(即编码器-解码器)[19-20]三种方法进行比较，结果显示在地磁活动频繁时期模型的预测效果都会变差，但是LSTM在磁暴时期会取得更好的效果.

本文采用深度学习的基本方法来进行电离层TEC的预测，时间精度相比以往的大部分论文来说更高，为1 h. 预测的TEC空间尺度是全球，空间经度分辨率为5°，纬度分辨率为2.5°，即每个TEC map的形状尺寸为71行、73列. 神经网络采用的是编码器-解码器结构[19]，其中，使用卷积层并且配合池化层来进行特征提取和降维便于加快网络训练和减小数据规模，中间层使用基于卷积操作的LSTM网络——ConvLSTM网络来实现时间序列预测的功能[21].

1 数据和实验方法

1.1 数据来源和预处理

电离层TEC数据集为IGS提供的标准IONEX(IONosphere map EXchange format)文件格式生成的全球电离层TEC数据. 时间分辨率是1 h；空间经度范围从西经180°到东经180°，分辨率是5°；纬度范围从北纬87.5°到南纬87.5°，分辨率是2.5°. 数据集的时间范围从1998-01-01—2018-12-31，每一天的数据构成一个文件. 根据以上信息即可得到全球TEC map网格点的规模是71×73.

另外，根据电离层TEC数据存在周期性的日变化规律，我们可以把一天的TEC map数据，即24个按时间顺序的TEC map合并作为一个单个样本的输入，该样本的输出为下一天的24个TEC map. 按照这种结构对所有的原始IONEX格式文件进行提取、拼接和重新设置矩阵维度信息等操作，我们可以得到一个五维张量，它的各个维度的大小是(number, 24,71, 73, 1). 其中：number代表了数据集的总样本个数；24代表每个样本包含24个小时，即24张如图1的TEC map；71和73则是每个整点时刻的TEC map的维度；1表示该map的颜色通道数目，因为每个经纬度的TEC是一个一维的数值.

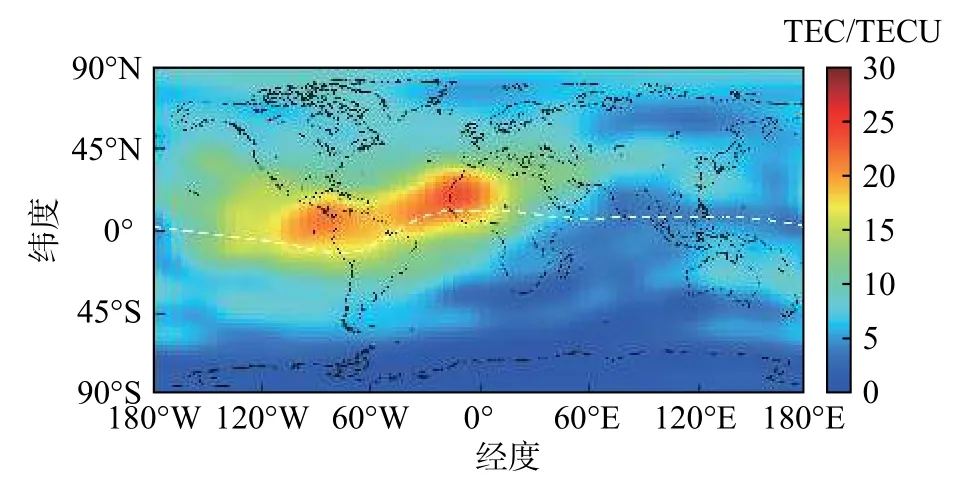
图1 2018-07-07T18:00的全球TEC mapFig. 1 The global TEC map of 2018-07-07T18:00

我们可以很容易地使用Python代码把一个时间序列数据转变成一组有监督学习的数据样本，数据序列的变化如图2所示，其中的每个数字代表了一整天24个整数时刻的TEC数据，是一个(24,71, 73, 1)形状的四维张量，且这些数据是按日期顺序递增排列的. 例如，图中的数字1,2,3可以表示为2017-01-01—03的TEC数据.

图2 时间序列数据转换为有监督数据的过程Fig. 2 Transform a time series data into a set of supervised learning data samples

本文选取1998-01-01T0:00—2017-12-31T23:00的数据作为训练集(占据总数的95%)和验证集(占据总数的5%)，2018-01-01T0:00—12-31T23:00的数据作为测试集，数据集划分和每个样本的输入及输出维度具体如表1所示.

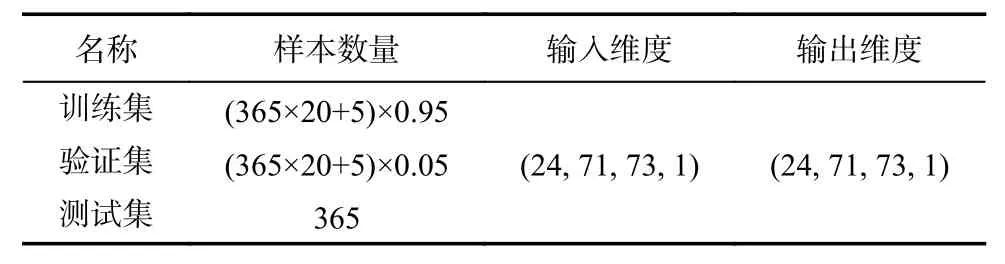
表1 数据集划分及样本维度Tab. 1 The scale and division of data set

1.2 神经网络模型的选取

本文采用深度学习的方法来对全球电离层的TEC map进行预测，使用经典的编码器-解码器框架来搭建深度神经网络[19]. 这个框架也被称为自编解码器，它主要的目的就是将输入网络的向量通过编码器转换为维度更低的中间向量，再利用解码器把这个中间变量转换为输出变量. 在深度学习中，编码器实现了特征降维的功能，相当于一个特征提取器；解码器会把编码的结果还原为需要的数据. 在图像处理领域，如手写数字的识别，自编解码器有着非常广泛的应用.

编码器-解码器的典型结构如图3所示. 其中：xi表示输入此框架的原始数据展开成一维后的第i个分量，pi表示经过编码器结构后得到的向量的第i个分量，yi表示通过此框架后输出的向量的第i个分量.

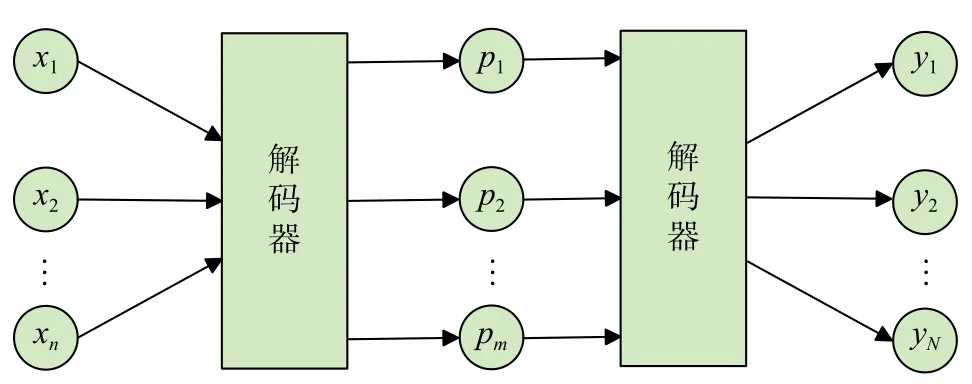
图3 编码器-解码器模型结构Fig. 3 The structure of encoder-decoder model

目前深度学习常用的网络模型是卷积神经网络(convolutional neural networks, CNN)和循环神经网络(recurrent neural network, RNN)，从它们的实现原理来看，前者更擅长提取空间结构信息，后者比较适合处理时间序列数据. RNN模型的众多实现中包括独立循环神经网络(independently recurrent neural networks，IndRNN)、门控循环单元(gate drecurrent unit, GRU)、LSTM网络等结构. LSTM网络凭借它的性能和效率成为了使用最广泛的一个网络模型. 但是单纯的LSTM网络对于同时存在时间和空间特征的电离层TEC数据就存在一定的局限性，所以本文采用了施行健等人[21]在2015年提出的ConvLSTM网络模型，其原理如图4所示. 它通过将矩阵乘法更改为元素卷积的方式实现了对空间局部特征的提取.

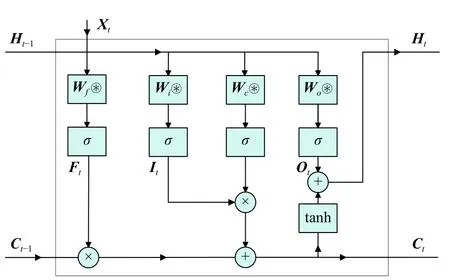
图4 ConvLSTM网络原理框图Fig. 4 The functional block diagram of ConvLSTM网络

LSTM网络使用输入门、输出门、遗忘门以及与隐藏状态相同的记忆细胞来记录额外的信息. 所有门的输入均由当前时刻t的输入Xt与上一时刻t−1的隐藏状态Ht−1组成，用W与b表示各部分的权重和偏置系数，Ct表示t时刻的状态，Ft为经过遗忘门后的输出结果，It为经过输入门后的输出结果，Ot为经过输出门后的结果，图4中的×表示元素对应位置点乘，公式中使用符号⊙表示，⊛表示卷积，根据原理框图有以下式子成立：

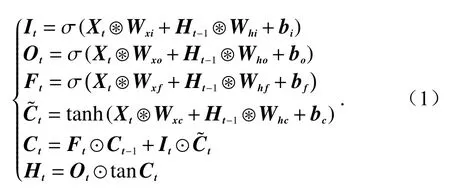
1.3 网络模型的构建和网络参数的选取

本文采用基于深度学习的神经网络结构，主要可以分为三个部分：第一部分为编码器，也就是卷积层和池化层的成对组合，它们可以将输入的电离层TEC map进行下采样，有效提取出数据的空间关键特征，同时池化操作也可以降低数据的维度，此操作可以减少神经网络的训练参数来加快训练过程；第二部分是一层ConvLSTM网络和一层批次标准化Batch Normalization，前者是实现时间序列预测的关键部分，可以提取出TEC map的时序特征，后者是对数据进行规范化，还可以防止过拟合；最后一个部分是根据编码器-解码器框架创建的与第一部分对应的卷积层和上采样层的成对组合，即解码器. 图5是构建好的网络模型结构.

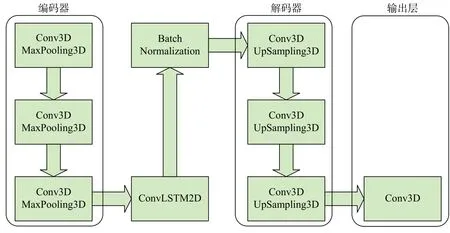
图5 本文搭建的模型结构Fig. 5 The structure of deep learning model in this paper

每一层的激活函数均采用elu函数，然后进行编译. 编译主要涉及损失函数、优化器和指示列表三个参数. 本文调整参数多次试验最终确定损失函数采用均方误差(mean-square error, MSE)，优化器使用改进后的自适应调整学习率的Adamax算法[22]. 训练轮数为100，批次大小为32.

2 结果和分析

按照图5中的网络结构框图，使用Python语言基于高度抽象的Keras库编写深度学习代码(后端采用TensorFlow)，搭建神经网络. 通过不断地调整每一层的内核大小以及滤波器数目最终得到训练好的模型，图6为训练过程中损失函数随轮数的变化曲线，可以看出验证集误差和训练集误差都随训练轮数的增加而逐渐下降并最终趋于水平稳定.

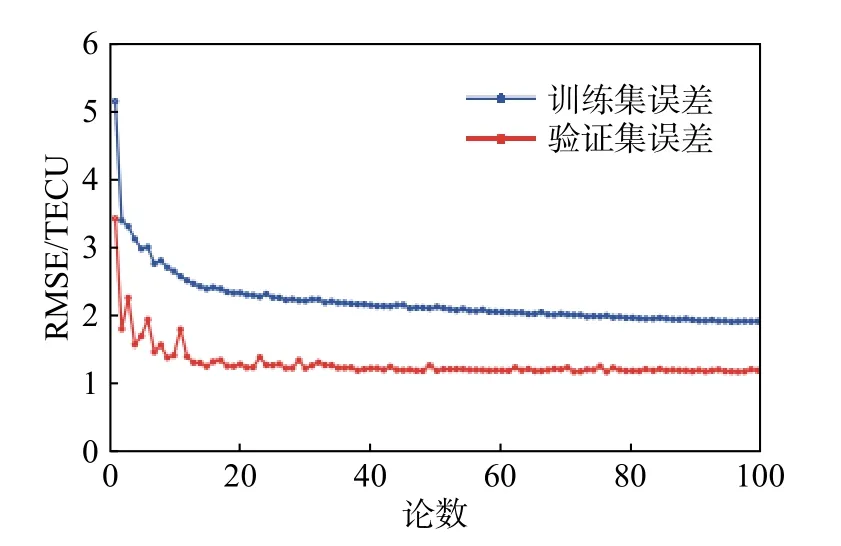
图6 训练误差随轮数的变化Fig. 6 The relationship between loss and epoch

本文采用每个TEC map的均方根误差(root mean square error, RMSE)来对模型的性能进行评价，RMSE公式为

式中：N表示每一个TEC map的数据个数，即71×73；TECp表示预测得到的TEC map；TECr表示根据实测数据得到的TEC map；i表示此TEC map的第i个数据点. 另外，由于模型的输入和输出为某一天的TEC数据，即24个TEC map，所以我们定义模型的RMSE公式为

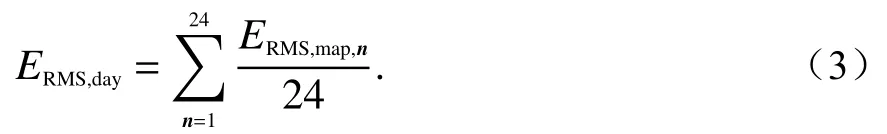
式中，ERMS,map,n表示第n个TEC map的RMSE.

下面讨论在不同情况下本文模型对全球TEC分布图的预测性能.

文中使用地磁活动指数Dst来判断是否处于磁暴时期[23-24]，如表2所示.

表2 磁暴类型的划分Tab. 2 The thresholds for storms

1)模型在训练集上，且处于磁平静时期(无磁暴)，提前1天的预测结果(图7). 图7(a)表示训练集上，当输入样本为2017-12-13的TEC数据时，即输入24×71×73×1的四维张量，模型预测得到的下一天的数据. 它与输入数据的维度是相同的，其中包含24个时刻的TEC map，即从当天的0:00到23:00，图中我们选择10:00的TEC map进行展示. 2017-12-14T10:00的实际台站观测并处理得到的TEC数据如图7(b)所示，使用公式(2)计算得到预测的RMSE为1.366 8，这表明预测的结果与实际TEC的数据误差很小.

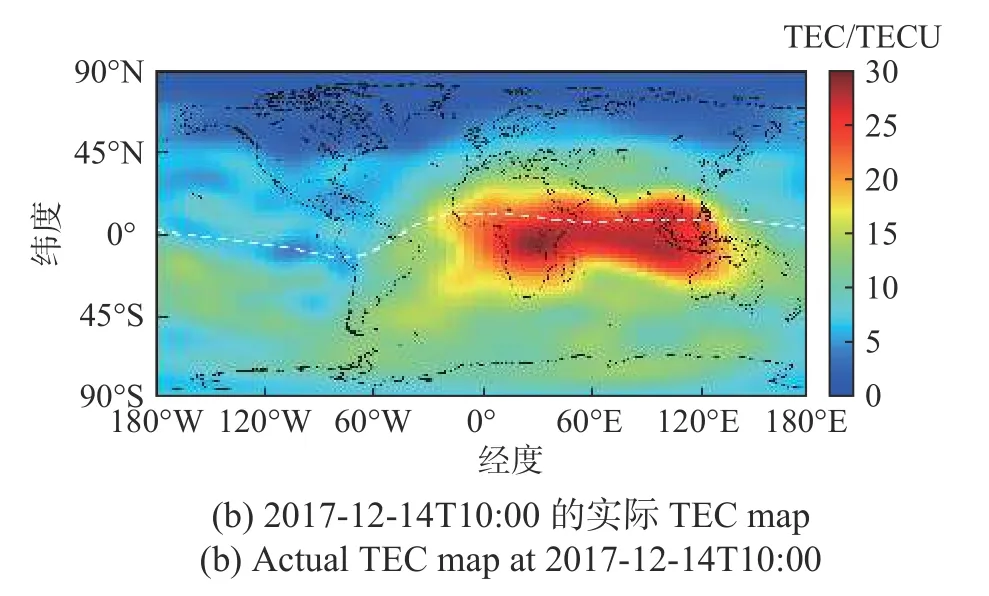
图7 磁平静时期在训练集的提前1天的预测结果(RMSE=1.366 8)Fig. 7 The one-day-prediction of model during the geomagnetic quiet time on the training set(RMSE=1.366 8)

2)模型在训练集上，且处于磁平静时期，提前2天的预测结果(图8). 模型在训练过程中的输入是前一天的24张TEC map数据，输出是神经网络预测得到的当天的24张TEC map数据. 在这里，我们把预测得到的这一天内的TEC map当作模型的输入，再次使用模型来进行预测，此时我们就可以得到提前2天的预测结果. 当模型的输入数据仍然是2017-12-13的TEC数据，根据这一方法，我们可以预测得到2017-12-15的数据. 图8(a)是这个数据在18:00的TEC map，图8(b)是实际观测的TEC数据.

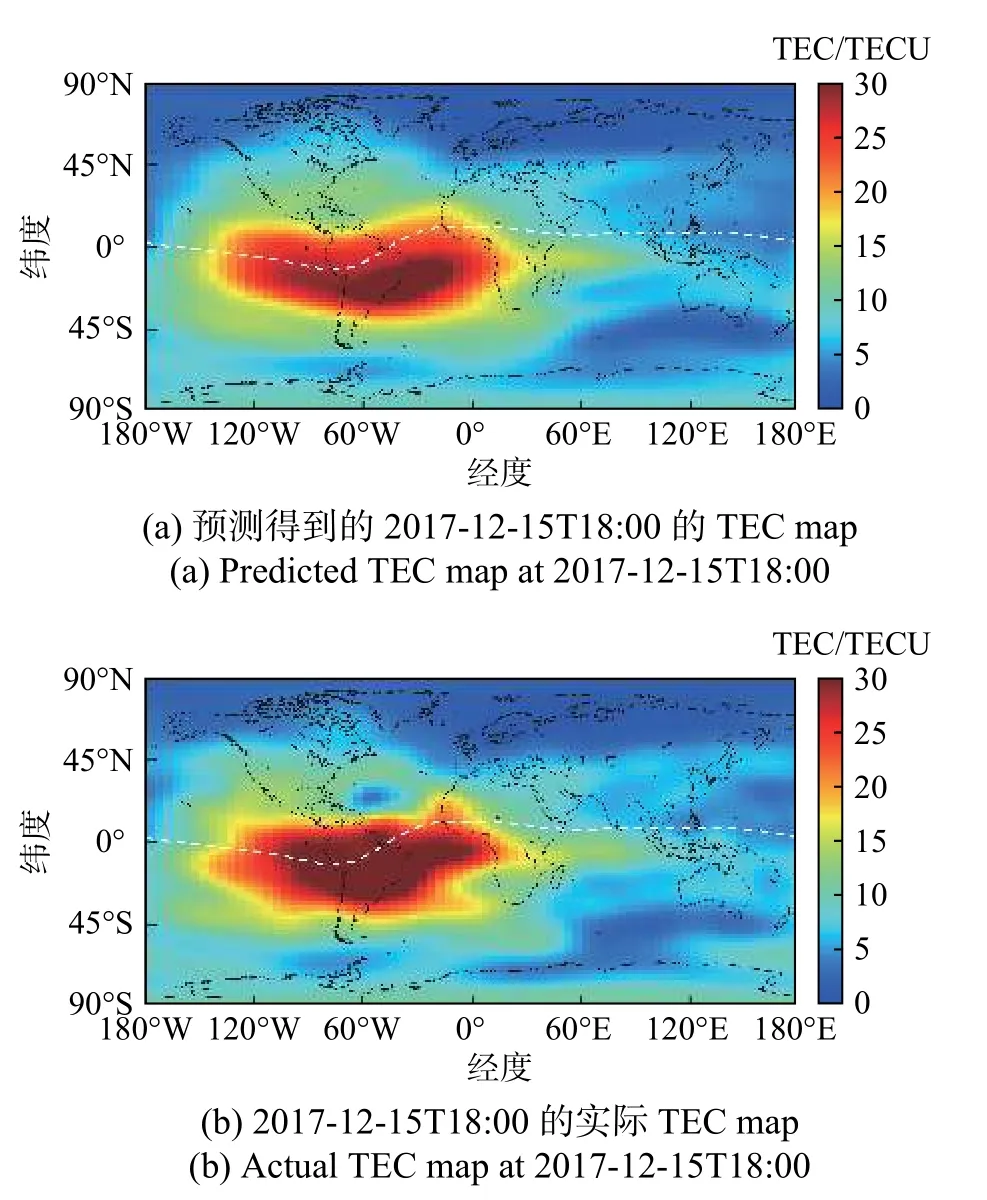
图8 磁平静时期在训练集的提前2天的预测结果(RMSE=1.564 4)Fig. 8 The two-day-prediction of model during the geomagnetic quiet time on the training set(RMSE=1.564 4)

3)模型在训练集上，且处于磁平静时期，提前7天的预测结果(图9). 其中输入样本仍为2017-12-13的TEC数据，模型预测得到2017-12-20的数据，图9(a)是这个数据在22:00的TEC map，图9(b)是实际观测的TEC数据.

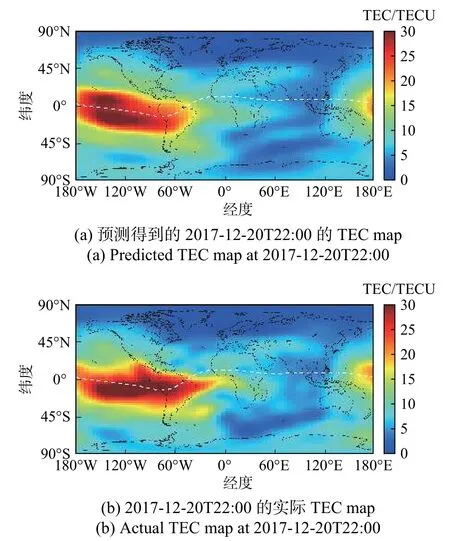
图9 磁平静时期在训练集的提前7天的预测结果(RMSE=2.129 1)Fig. 9 The seven-day-prediction of model during the geomagnetic quiet time on the training set(RMSE=2.129 1)

使用已经训练好的模型对整个测试集的数据进行提前1天的电离层TEC预测误差分析，利用式(3)得到每次预测的RMSE，误差的分布直方图如图10所示.

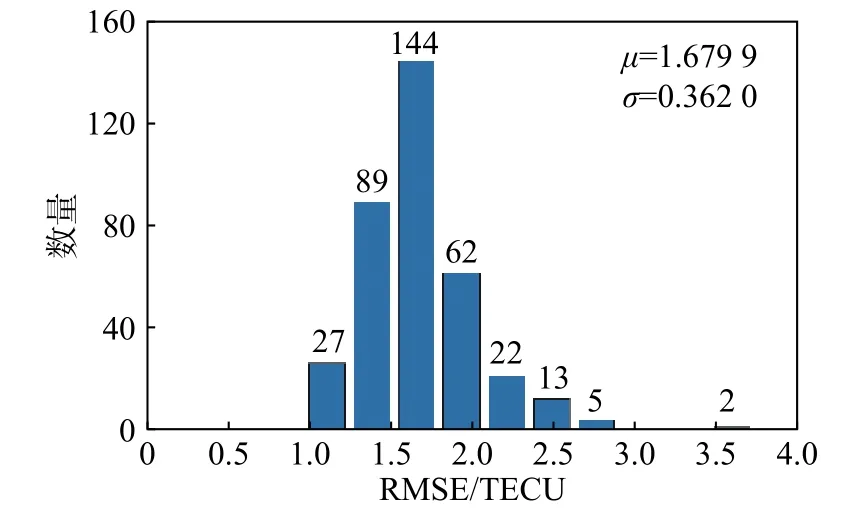
图10 模型在测试集上的预测误差分布直方图Fig. 10 the histogram of prediction error on the test set

从图10可以看出，模型在测试集上的误差的均值为1.679 9 TECU，而且误差的标准差为0.362 0 TECU，这表明模型的预测效果很稳定. 图中误差在3.5 TECU的两次预测是在中等磁暴和强磁暴的情况下得到的预测结果. 模型在弱磁暴和磁平静时期的预测效果非常稳定，而且误差很小，下面给出了在不同地磁活动水平下模型的预测效果.

1)模型在测试集上，且处于磁平静时期，提前2天的预测结果(图11). 其中输入为2018-12-15的TEC，预测得到2018-12-17的数据，图11(a)是这个数据在5:00的TEC map，图11(b)是实际观测的TEC数据.

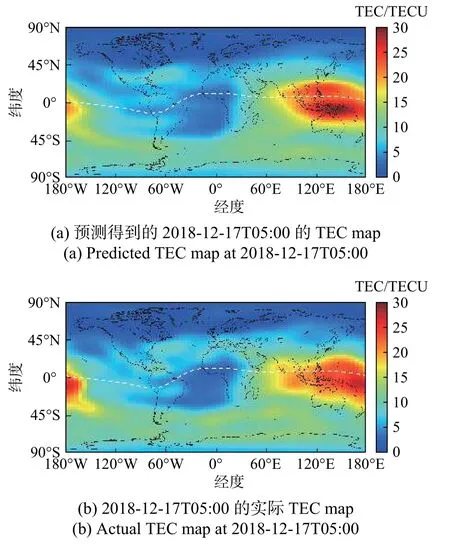
图11 磁平静时期在测试集的提前2天的预测结果(RMSE=1.426 0)Fig. 11 The two-day-prediction of model during the geomagnetic quiet time on the test set(RMSE=1.426 0)

2)模型在测试集上，且处于弱磁暴时期，提前1天的预测结果(图12)，其中输入样本为2018-09-10的TEC数据，模型预测得到2018-09-11的数据，图12(a)是这个数据在5:00的TEC map，图12(b)是实际观测的TEC数据.

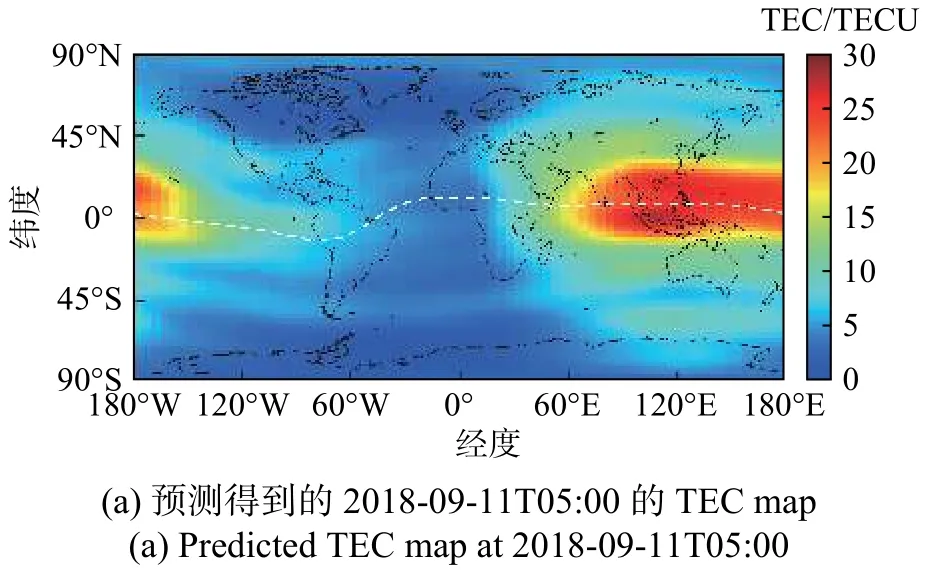
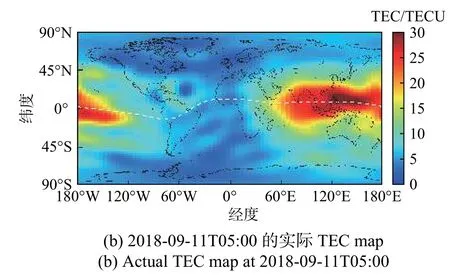
图12 弱磁暴时期在测试集的提前1天的预测结果(RMSE=2.204 7)Fig. 12 The one-day-prediction of model during the geomagnetic small storm on the test set(RMSE=2.204 7)

3)模型在测试集上，且处于中等磁暴时期，提前1天的预测结果(图13). 其中输入样本为2018-04-19的TEC数据，模型预测得到2018-04-20的数据，图13(a)是这个数据在5:00的TEC map，图13(b)是实际观测的TEC数据.

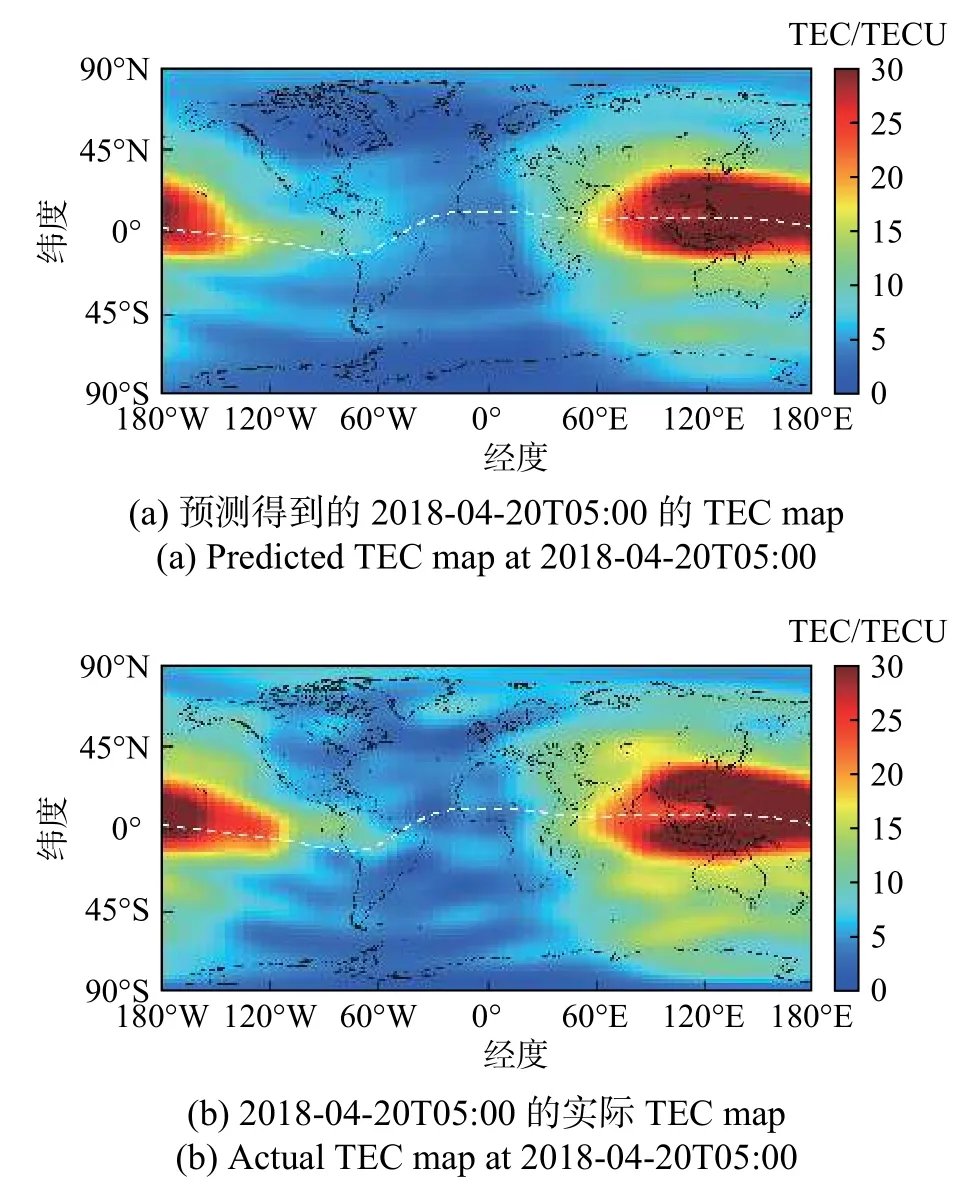
图13 中等磁暴时期在测试集的提前1天的预测结果(RMSE=2.441 7)Fig. 13 The one-day-prediction of model during the geomagnetic moderate storm on the test set, RMSE=2.441 7

4)模型在测试集上，且处于强磁暴时期，提前1天的预测结果(图14). 模型预测得到2018-08-26T5:00的TEC map为图14(a)，图14(b)是实际观测的TEC数据.

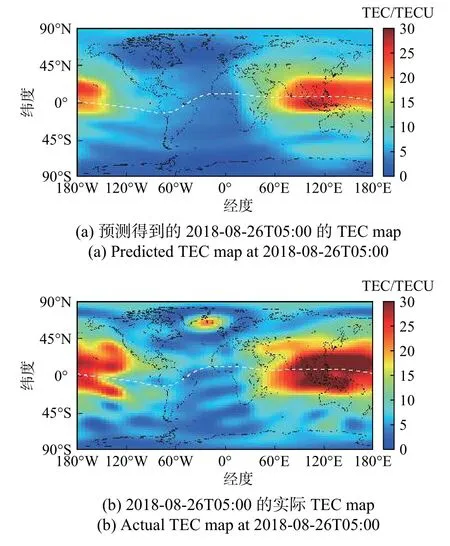
图14 强磁暴时期在测试集的提前1天的预测结果(RMSE=4.549 1)Fig. 14 The one-day-prediction of model during the geomagnetic intense storm on the test set(RMSE=4.549 1)

图7～14表明模型在训练集和测试集取得相近的效果. 另外，模型对于提前1天的TEC预测效果要好于提前2天和7天的预测效果，即随着天数的增加，模型的预测效果会逐渐变差；模型在磁暴时期的预测相对于磁平静时期误差更大. 图11～14是在不同的地磁活动条件下，模型对于提前1天预测得到的24个TEC map的其中一张与实际进行对比并计算误差. 图15是对这24张TEC map的每个时刻分别计算误差，可以看出随着磁暴的剧烈程度增加，模型的预测效果也会变差.

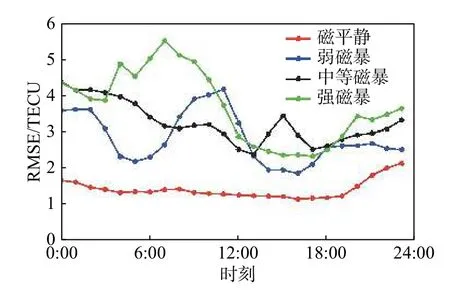
图15 不同磁暴条件下提前1天预测的不同时刻的RMSEFig. 15 One-day prediction of RMSE at each hour in different storms

下面研究同一天不同经纬度位置下模型提前预测1～7天的结果，如图16所示. 可以看出，模型在高纬度的预测效果要优于低纬度的预测效果.

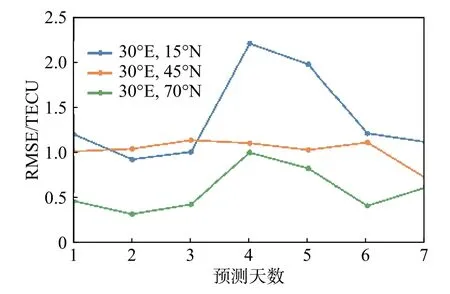
图16 模型在不同纬度连续提前7天预测的RMSEFig. 16 Seven-day prediction of RMSE at different latitudes

接下来研究模型进行提前1天TEC预测时的误差与当天不同时刻的关系. 图17中的每条曲线是模型提前1天预测的RMSE，曲线上的点表示在特定时刻的误差，mean_rmse表示图中5次预测误差的平均值. 这表明模型对于TEC数据的预测效果基本不会受到一天不同时间段的影响.

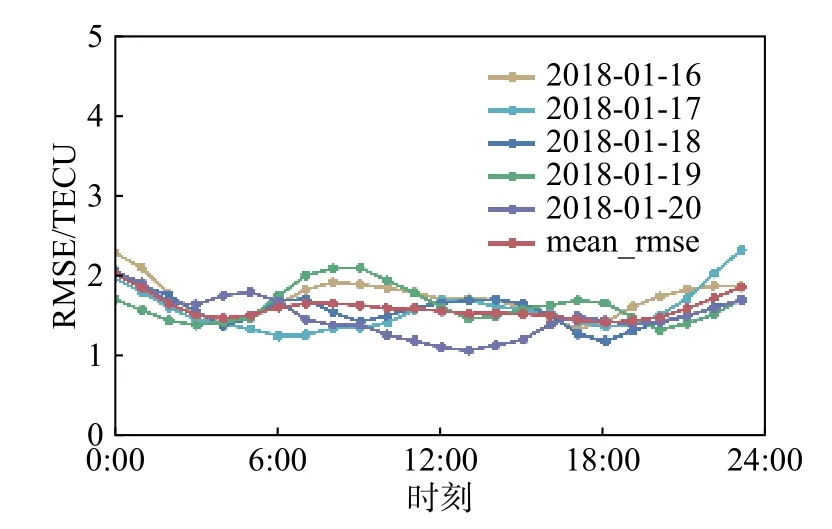
图17 提前1天预测的不同时刻的RMSEFig. 17 One-day prediction of RMSE at every hour

3 结 论

针对全球电离层TEC的时空预测问题，本文提出了一种基于深度学习方法的全球电离层TEC预测模型，采用编-解码器结构配合卷积优化的长短时记忆网络(ConvLSTM)实现了全球TEC数据的高时间精度和空间分辨率的预测. Song等人使用遗传算法改进的神经网络对中国地区TEC的预测误差在5～8 TECU，Cesaroni等人使用神经网络的预测误差在3～5 TECU. 本文将全球范围的TEC预测误差下降到1.5 TECU左右，这一方面得益于CNN能够代替人工对数据进行特征工程，适合处理具有局部关联性和统计平稳性的数据，可以提取得到样本的空间特征；另一方面是运用ConvLSTM将卷积结合到LSTM网络实现了对数据的时序预测功能. 两者结合并选用合适的参数，最终得到了更好的预测效果.

通过研究模型在训练集和测试集上以及在不同磁暴条件和不同纬度下的效果，我们可以得到以下结论：

1)模型的预测误差随着预测时间的增加而逐渐变大. 对于提前1天的TEC预测，RMSE基本稳定在1.5 TECU以下；对于提前2天甚至7天的TEC预测也具有相当令人满意的结果.

2)随着磁暴的剧烈程度增加，模型的预测效果也会变差.

3)模型在高纬度下的预测效果要优于低纬度的预测效果，而且对于TEC数据的预测效果基本不会受到一天不同时间段的影响.

但是，模型对于磁暴时期的TEC数据预测还存在较大误差，需要进一步的研究工作：一方面，电离层与太阳风、磁层以及电离层不同纬度区之间有着复杂的耦合过程[25]，可以考虑将太阳风等参数加入模型来进行训练；另一方面，目前除了ConvLSTM网络以外还有Attention机制、GRU以及Transform等内容可在深度学习算法中使用，可以借助相关技术实现更高精度的TEC预测.