基于自相关函数的SRSF信号感知矩阵优化方法
2021-09-02吕明久许鹏程陈文锋杨军赵欣
吕明久 许鹏程 陈文锋 杨军 赵欣
(空军预警学院,武汉 430019)
引 言
基于压缩感知(compressed sensing,CS) 理论[1]的随机步进频率(random stepped-frequency, RSF)信号高分辨成像技术通过对目标固有稀疏特性的利用,可以实现在较少发射子脉冲条件下的高概率目标重构,适用于现代雷达系统多工作模式以及干扰条件下的高精度成像. 其中,性能优越的量测矩阵是提升稀疏重构性能的重要保证,因此通过对量测矩阵进行优化来减少观测数据与提升稀疏重构性能已成为学者专注的热点领域[2-3].
当前,已经提出多种量测矩阵的优化设计方法.其中,减小感知矩阵(量测矩阵与稀疏基)的互相关性是较为常见、有效的优化手段,主要采用包括高斯[4]、亚高斯[5]以及Chaotic[6]等随机性较强的量测矩阵来保证感知矩阵的互相关性要求[7-9]. 这类矩阵在实际运用中具有产生困难、系统实现难度大的问题. 此外,这一类的感知矩阵优化通常是基于一个选定初始矩阵的迭代优化过程,因此并没有考虑通过对发射波形参数的优化实现重构性能的提升. 而对于稀疏RSF(sparse RSF,SRSF)信号,其随机稀疏发射过程与CS的随机量测过程相一致,即量测矩阵为随机部分单位阵,因此可以避免引入新的量测矩阵,而是直接将感知矩阵设计问题转化为对SRSF信号的波形设计问题[10]. 文献[11-12]中以感知矩阵互相关性为目标,自适应地构造发射波形和测量矩阵,达到了提升重构性能的目的. 这也是目前基于波形优化的感知矩阵设计常用的手段之一. 实际上,传统波形优化设计问题大都从信号匹配处理的角度出发研究如何设计和产生模糊函数(ambiguity function,AF)最优的发射信号,这类方法具有理论体系完善、物理意义明确以及实现简单等优点[13]. 从表面上看,感知矩阵性能优化与传统基于AF的波形设计方法具有明显的差别. 前者是一种基于凸优化理论的优化,其性能主要由感知矩阵的互相关性决定. 而后者是一种基于匹配滤波理论的波形设计方法,波形的分辨性能和测量精度与模糊图的主峰尖锐程度以及旁瓣高低有关. 文献[14]从AF的角度分析了不同波形的稀疏重构,文献[15]指出选择具有较低旁瓣AF的波形可以提高MIMO雷达的成像质量,文献[16]中也对上述问题进行了初步研究,可以看出,AF同样会影响信号的稀疏重构性能. 但从目前来看,对这两者之间的内在联系分析还并不深入,值得进行进一步的研究与探索.
针对上述问题,本文基于感知矩阵优化理论并结合步进频率波形特征,提出了一种基于自相关函数(AF的零多普勒切面)的RSF信号感知矩阵优化方法. 首先,在构建稀疏重构模型的基础上,分析了SRSF信号波形参数与感知矩阵构造方式的内在联系,得出了感知矩阵互相关系数矩阵为对称Toeplitz矩阵的结论. 然后,证明了互相关系数矩阵与信号AF矩阵的关系,得出在特定条件下,两者等价的结论. 因此,将SRSF信号重构的二维感知矩阵优化问题转化为基于一维自相关函数的波形优化设计问题. 最后,为验证上述结论,给出了一种基于自相关函数最大旁瓣与均值旁瓣联合约束的稀疏波形设计方法. 本文的研究揭示了感知矩阵优化理论与传统AF波形优化理论的内在关系,进一步丰富了稀疏波形设计方法. 此外,由于将二维矩阵优化转换为一维向量设计问题,因此,给出的稀疏波形设计方法具有物理意义明确、计算量小、容易实现等优点. 理论分析与仿真实验验证了所提方法的有效性.
1 基于SRSF信号的稀疏重构模型
SRSF信号可以视为传统步进频率信号的随机抽取样式,文献[17]中给出了步进频率信号的回波采样形式,假设目标已经经过运动补偿,此时第n脉组内的回波采样信号可以写成

式中:σk为散射点强度;K为散射点个数;Rk为第k个散射点与雷达的初始距离;wn为噪声;载频步进fn表达式为
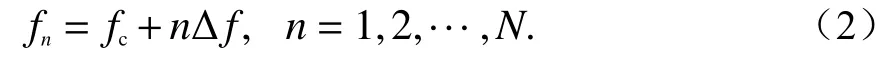
式中:fc为载频;Δf为步进频率间隔;N为子脉冲个数. 将目标在距离域划分为[R1,R2,···,RP]个网格,可得到一个P×1维的目标距离像矩阵. 此时,式(1)可以表示为

式中,

式(3)写成矩阵形式可表示为

式中:x=[R1,R2,···,RP]T∈RP×1为距离像;W′为噪声向量;Ψ为N×P(N≤P)维稀疏基矩阵,构造方式为

对于SRSF信号,假设用矩阵Φ表示信号随机稀疏发射的规律,则发射规律Γ可以表示为

式中:Π=[1,2,···,N]T为传统步进频率信号子脉冲发射规律;Γ=[Γ0,Γ1,···,ΓM−1],Γi∈[1,N]且|Γ|=M,M≤N,|·|表示集合的势,即包含的非零元素个数;矩阵ΦM×N=[ϕi,i′]的构造方式可以写成如式(8)所示的随机部分单位阵形式.

此时依据式(5),SRSF信号的稀疏表示形式可以写成

从上述分析可知,量测矩阵Φ可以视为对传统步进频率信号的随机量测,因此不需要再设计新的量测矩阵. 另外,Φ是根据SRSF信号的随机稀疏情况进行设置,与信号的随机发射规律、发射子脉冲个数等相关,因此通过对SRSF信号进行波形设计可以改变量测矩阵Φ的构造方式,进而影响信号的稀疏重构性能. 下面基于上述稀疏重构模型,研究基于波形设计的优化方法,实现SRSF信号稀疏重构性能的提升.
2 基于波形设计的感知矩阵优化
2.1 感知矩阵互相关性与自相关函数的关系
为定量化描述基于CS理论的稀疏重构性能,Donoho[18]提出了感知矩阵Θ的非相关性约束条件.其中,最大互相关系数µmax以及平均互相关系数µκ_ave能够较为全面、客观地描述感知矩阵的互相关性,µmax用于衡量感知矩阵Θ中各列之间的相关性,而µκ_ave则是衡量感知矩阵Θ平均互相关性能的重要指标. µmax和µκ_ave越小,表明Θ的整体相关性较弱,相应的稀疏重构性能便越好[19]. µmax和µκ_ave分别定义为:

式中:Θi代表矩阵Θ的第i列;〈·,·〉表示内积;µi,j为矩阵Θ第i列与第j列数据的互相关系数值;κ∈[0,1],当κ=0时,µκ_ave表示感知矩阵Θ中所有列之间互相关系数的均值.
实际上,感知矩阵Θ的最大互相关系数也可表示为感知矩阵所对应的Gram矩阵G中非对角线上元素的最大值[19]. 对于SRSF信号的稀疏重构模型式(9),其Gram矩阵G展开形式为

此时,Gram矩阵G中的元素分别代表感知矩阵Θ的第i列与第j列的互相关系数µi,j. SRSF信号载频步进方式可以视为RSF信号载频随机置零形式. 需要注意的是,未发射脉冲的位置可以视为相应位置载频fn为0. 因此,µi,j可以表示为

式中,ΔR为 距离维离散间隔. 此时,最大互相关系数可以表示为
从式(13)可以看出,在距离离散间隔确定的情况下,µi,j的取值主要由 (i−j)确定. 对于Gram矩阵G每个对角线上的元素,其 (i−j)的取值是相同的,因此,Gram矩阵G中任何一条对角线上的元素取值相同,由此可知Gram矩阵G为Toeplitz矩阵. 又由于,因而Gram矩阵G为对称Toeplitz矩阵. 根据对称Toeplitz矩阵的定义可知,其第一行元素就可以完全描述整个矩阵的性能[20]. 此时,Gram矩阵G中第一行元素可以表示为
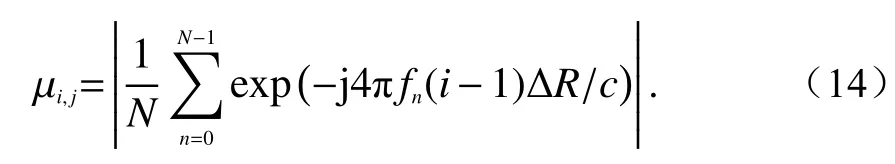
而根据AF理论,SRSF信号的AF可以表示为[13]
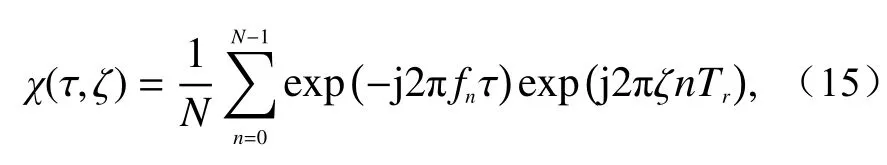
Tr为子脉冲周期.
假设在一个脉冲周期内,距离域、多普勒域的离散采样点数分别为P、Q. 此时式(15)可以转化为

式中,Δτ与Δζ分别为时延、多普勒域离散采样间隔.根据时延、多普勒域与距离、速度域的对应关系,式(16)可以化为

式中,Δr与Δυ分别为距离、速度域离散采样间隔. 当p=q=0时,χ(τp,ζq)取最大值,也即AF的峰值位置;当p、q不等于0时,χ(τp,ζq)表示AF的旁瓣.
依据式(17),当速度为零时,信号的互相关函数(AF的零多普勒切面)可以表示为

对比式(14)与式(18)可知:在距离离散采样间隔相等的情况下,感知矩阵的互相关系数与信号的自相关函数具有相同的表达形式,两者是等价的. 此时感知矩阵Θ的最大互相关系数µmax可以用自相关函数表示为

从式(19)可以看出,感知矩阵最大互相关系数µmax即对应着自相关函数最高旁瓣的绝对值.
根据式(11),平均互相关系数µκ_ave也可以用信号自相关函数表示为

此时,感知矩阵Θ的平均互相关系数µκ_ave等价于信号自相关函数旁瓣的均值.
从以上分析可知SRSF信号的自相关函数与感知矩阵的互相关系数具有等价关系. 因此,这也为SRSF信号的感知矩阵优化提供了一种新的设计思路,即可以将感知矩阵优化问题转化为基于自相关函数的SRSF信号波形优化设计问题,通过对SRSF信号自相关函数旁瓣水平进行优化设计,不仅能够避免引入新的量测矩阵,而且可以优化感知矩阵,达到提高信号稀疏重构性能的目的. 基于上述分析,下面提出一种基于波形设计的SRSF信号感知矩阵优化方法.
2.2 基于自相关函数最大旁瓣与均值旁瓣联合约束的遗传寻优方法
由上一节分析可知,对Gram矩阵G的优化问题可等效为对稀疏信号自相关函数的优化. 此时感知矩阵优化目标可以转化为使得稀疏信号自相关函数峰值为1,旁瓣最低. 基于此,本节给出一种基于自相关函数最大旁瓣与均值旁瓣联合约束的感知矩阵优化方法.
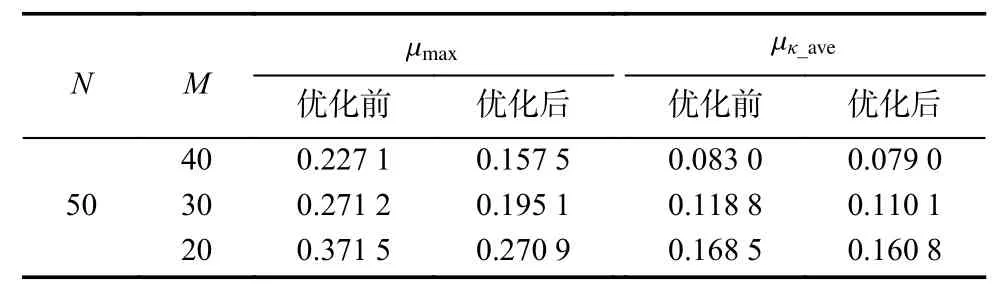
对SRSF信号进行波形设计主要包括子脉冲步进方式以及子脉冲稀疏的位置等两个参数. 从式(18)可以看出,SRSF信号的自相关函数为求和形式,子脉冲的跳变顺序并不会影响最终的结果,因此在进行SRSF信号波形设计时,主要考虑在确定发射子脉冲个数M(M 图1 SRSF信号波形设计示意图Fig. 1 Waveform design diagram of SRSF signal 目前,用于衡量信号自相关函数旁瓣水平的指标主要有积分旁瓣比、均值旁瓣比,这两种指标分别基于自相关函数的最大旁瓣以及均值旁瓣,其对应的计算方法可以表示为: 当PSLR、ISLR值越小时,说明旁瓣水平越低.为提高信号自相关函数设计的鲁棒性与有效性,此处给出一种峰值旁瓣以及均值旁瓣联合约束条件下的波形优化方法,对应的载频步进序列优化目标函数可以表示为 式中:λ∈[0,1]表示权重系数,可以根据实际情况实时调节各优化因素的权重;N为子脉冲个数;表示需要优化的M个发射子脉冲序列;O(ΓM) 表示ΓM中元素的个数. 对于式(23)所示的优化问题,目前有多种求解算法,如梯度下降法、蚁群算法以及遗传算法等. 由于上述问题非凸,其中遗传算法能以最大概率搜索到全局的最优解,因此本文利用遗传算法对上述优化问题进行寻优. 算法实现主要流程可表示为[21]: 1) 初始化. 首先根据子脉冲个数M,在集合[1,···,N]中随机产生初始种群,即产生L组随机编码序列,记 2) 评价. 以自相关函数的最大旁瓣以及均值旁瓣水平为适应度函数,对种群进行适应度评价. 此时的适应度函数可以表示为 由于自相关函数最大旁瓣以及均值旁瓣值较小,且随着优化过程会变得更小,为提高优化的效率,此处通过设置惩罚函数 γ(0<γ<1)以及倒数形式为新的自适应函数,可以表示为 此时,第l个序列对应的选择概率可以表示为 3) 选择. 按照选择概率对种群进行选择操作,选择适应性强的编码序列并保存. 4) 交叉与变异. 采用单点交叉以及均匀多点变异方式对种群进行交叉与变异操作,并设置交叉概率和变异概率(本文中设置交叉概率为0.6,变异概率为0.5). 5) 对上述步骤2~4进行循环操作,当最大旁瓣以及均值旁瓣达到设计要求或者循环达到最大遗传代数时输出最终结果. 通过上述遗传寻优方法,可以得到自相关函数旁瓣电平优化后的SRSF信号,根据信号自相关函数与感知矩阵的关系,也即得到性能更优的感知矩阵,从而提升SRSF信号的稀疏重构性能. 本节主要对SRSF信号自相关函数与感知矩阵之间的关系进行仿真验证,并对提出的优化方法进行仿真. 首先给出信号采样率计算方式为α=M/N,即发射子脉冲信号越多,信号采样率越高. 估计误差计算方式为,其中x、xˆ 分别为参数的真实值与估计值,‖·‖F表示范德蒙范数. 仿真中采用正交匹配追踪(orthogonal matching pursuit, OMP)算法进行稀疏重构. 假设SRSF信号载频f0=10 GHz ,子脉冲脉宽T为1 µs,子脉冲重复频率PRF=2 000 Hz. 在合成带宽为250 MHz不变的条件下,设置子脉冲N为50,信号距离维离散点数P=1.2N. 此时构建相应的感知矩阵Θ并依据式(10)可以得到感知矩阵Θ的最大互相关系数值µmax,其结果如表1所示. 图2给出了随机发射部分子脉冲个数条件下相应的SRSF信号自相关函数结果,图中标示出了最大旁瓣的位置与幅值. 表1 SRSF信号最大互相关系数Tab. 1 The max mutual coherence of SRSF signal 对比表1以及图2的结果可以看出:在不同的发射子脉冲个数条件下,通过感知矩阵计算出的最大互相关系数值µmax与自相关函数的旁瓣最大值均相同. 因此,仿真验证了感知矩阵互相关系数与自相关函数旁瓣之间的关系. 图2 随机发射部分子脉冲个数条件下的自相关函数Fig. 2 The autocorrelation function of different transmitting subpulses 下面对所提的SRSF信号自相关函数优化方法进行仿真实验. 信号参数设置与3.1节相同,设置权重系数λ=0.3,初始种群个数L设置为50. 表2为优化前后感知矩阵最大互相关系数以及均值旁瓣值互相关系数(κ=0)的比较. 表2 优化前后的互相关系数变化Tab. 2 Variation of mutual coherence before and after optimization 从表2的结果可以看出:在不同的稀疏条件下,通过本文所提方法对自相关函数进行优化后的旁瓣水平均得到显著降低. 当M=20时,优化前最大旁瓣峰值为0.371 5,通过优化后的旁瓣峰值降低至0.270 9.因此本文所提基于自相关函数的SRSF信号波形设计方法可以显著优化自相关函数的旁瓣水平. 其他条件保持不变,采样率α=0.4,信噪比为20 dB,图3给出了有10个非零散射点条件下优化前后的SRSF信号稀疏重构结果对比. 为显示所提方法的有效性,设置同等维度的降维随机矩阵(M×N),采用文献[18-19]以及文献[22]中所提的方法进行感知矩阵优化(下文称之为Elad方法以及Saprio方法),利用优化后的随机矩阵进行稀疏重构. 图中目标散射点的位置与幅度值均为随机产生. 从仿真结果可以看出,在相同的稀疏度条件下,优化前稀疏信号的重构结果存在较多的虚假重构点,且在目标位置的幅度重构也存在较大的误差. 虽然通过Elad方法以及Saprio方法设计的随机量测矩阵进行稀疏重构时,重构结果的虚假重构得到一定程度的抑制,且重构幅度误差也进一步下降,但利用本文信号自相关函数的优化,SRSF信号重构结果的虚假点明显少于优化前的信号,真实位置的幅度重构误差也得到了显著减小,计算得到的误差分别为0.254 5、0.141 1、0.111 0以及0.041 2. 另外,Elad方法以及Saprio方法并没有通过对稀疏波形进行优化而提升重构性能,相比较而言本文方法利用波形稀疏信息进行感知矩阵设计,不仅提升了重构性能,且更适合于实际装备用于优化资源调度,从而显示了所提方法的优越性. 为进一步验证自相关函数优化后的SRSF信号稀疏重构性能,图3(e)给出了目标稀疏度K为10时,在不同信噪比条件下优化前后重构误差对比,蒙特卡洛次数设置为500. 从图3(e)的仿真结果可以看出,通过对不同稀疏度条件下的SRSF信号自相关函数进行优化,稀疏重构误差均得到了有效减小. 且随着稀疏度的降低,优化后的稀疏信号稀疏重构误差改善的幅度明显变大,这是由于通过波形设计减小了感知矩阵互相关系数(自相关函数旁瓣峰值),从而能够精确重构稀疏度更大的信号,这也验证了所提优化方法的正确性. 图3 不同方法稀疏重构结果对比Fig. 3 Comparison of reconstruction results via different methods 本文对SRSF信号自相关函数与SRSF信号稀疏重构所需感知矩阵互相关系数矩阵之间的关系进行分析,得出两者具有等价关系的结论,并基于此给出了一种基于自相关函数最大旁瓣以及均值旁瓣联合约束下的SRSF信号波形设计方法,验证了上述结论的正确性. 本文的研究结论将基于凸优化理论的系数重构性能优化方法与基于传统AF的波形设计方法相统一,拓展了稀疏波形设计方法范畴. 同传统基于凸优化的波形设计方法相比,本文所提方法具有物理意义明确、计算量小、容易实现等优点. 此外,基于互相关函数与信号稀疏重构性能的关系,可以进一步设计AF旁瓣水平更低的优化算法,提升稀疏波形的优化性能,这也是下一步需要重点研究的方向.

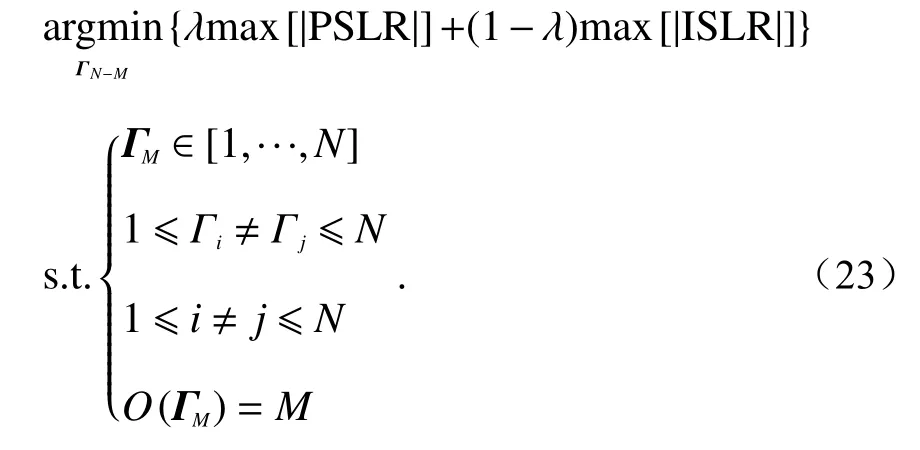


3 仿真分析与验证
3.1 自相关函数与感知矩阵互相关系数关系验证


3.2 基于波形优化的稀疏重构性能仿真


4 结束语
