基于Kriging修正模型的铁路捣固镐优化

王 杰，王 滔，叶 爽，郑慧珍，方 涵

（四川大学机械工程学院，四川成都610065）

随着我国铁路的迅速发展，运输量和运输频率逐渐增加，对铁轨的可靠性和安全性提出了更高的要求。内燃冲击捣固镐是一种广泛应用于铁路施工、维修作业中的小型养护机械，主要用于铁路道碴捣固作业［1］。冲击系统是捣固镐的核心部分，在作业过程中以高压气体为动力，驱动压气活塞及冲击内筒往复运动，将气体能量转化为机械能，使得轨枕底部道碴重新排列［2］，在特殊路段及偏远地区发挥着不可替代的作用。针对捣固镐的结构优化问题，因无法直接获得自变量与因变量的显示表达式，往往需要进行大量的计算，导致在实际工程优化中难度较大。而代理模型方法能显著提高工程优化问题的效率，具有计算量小、不降低精度等优点，在航空航天领域得到了广泛应用［3］，并逐渐发展成为一种结构优化方法。苏瑞意等［4］使用1阶多项式和2阶多项式响应面模型对客车车身骨架进行了设计优化，但1阶多项式和2阶多项式响应面对复杂非线性问题拟合度较差。徐兴伟等［5］使用Kriging响应面对门式起重机主梁进行优化设计，并采用有限元法验证了该代理模型结果的有效性。巩博瑞等［6］基于Kriging模型对水下检测装置的齿轮副机构进行了失效分析，表明了分析结果与工程经验相符。目前常用的代理模型有标准2阶型、Kriging、神经网络等。合理的响应面模型能根据少量的样本点数据建立起精确的设计变量与输出变量之间的关系。由于Kriging模型对非线性问题具有良好的效果，在计算效率和精度上有一定优势［7］，并且广泛应用于工程结构优化。鉴于此，本文以捣固镐冲击系统的零件模型为研究对象，提出一种多层修正Kriging方法，通过试验设计获取足够多具有代表性的样本数据，利用响应面全局精度检验点以及局部误差较大区域细化点作为修正Kriging模型的依据，不断更新以提高Kriging模型精度，直至满足精度要求，最后利用仿真平台验证了修正方法的可行性，为该类产品的设计及性能改进提供理论依据。

1 捣固镐工作原理

内燃捣固镐结构简图如图1所示。捣固镐作业时，将镐钎14插入轨枕下的石碴中，镐钎与冲击内筒8接触。发动机1输出的转速和扭矩，通过摩擦离合器2传递给齿轮减速机构3，减速机构调整转速和扭矩，并通过曲柄4带动连杆5运动，将回转运动转换为压气活塞7在冲击内筒中的往复运动。曲柄及连杆的原理为曲柄滑块机构。冲击内筒与压气活塞之间为密闭工作腔，工作腔中介质为空气。工作腔在压气活塞的往复运动作用下产生周期性变化的压强，不断吸附和驱动冲击内筒在外筒6中做直线往复运动，镐钎受到冲击内筒的周期性冲击，最终完成冲击能的输出。

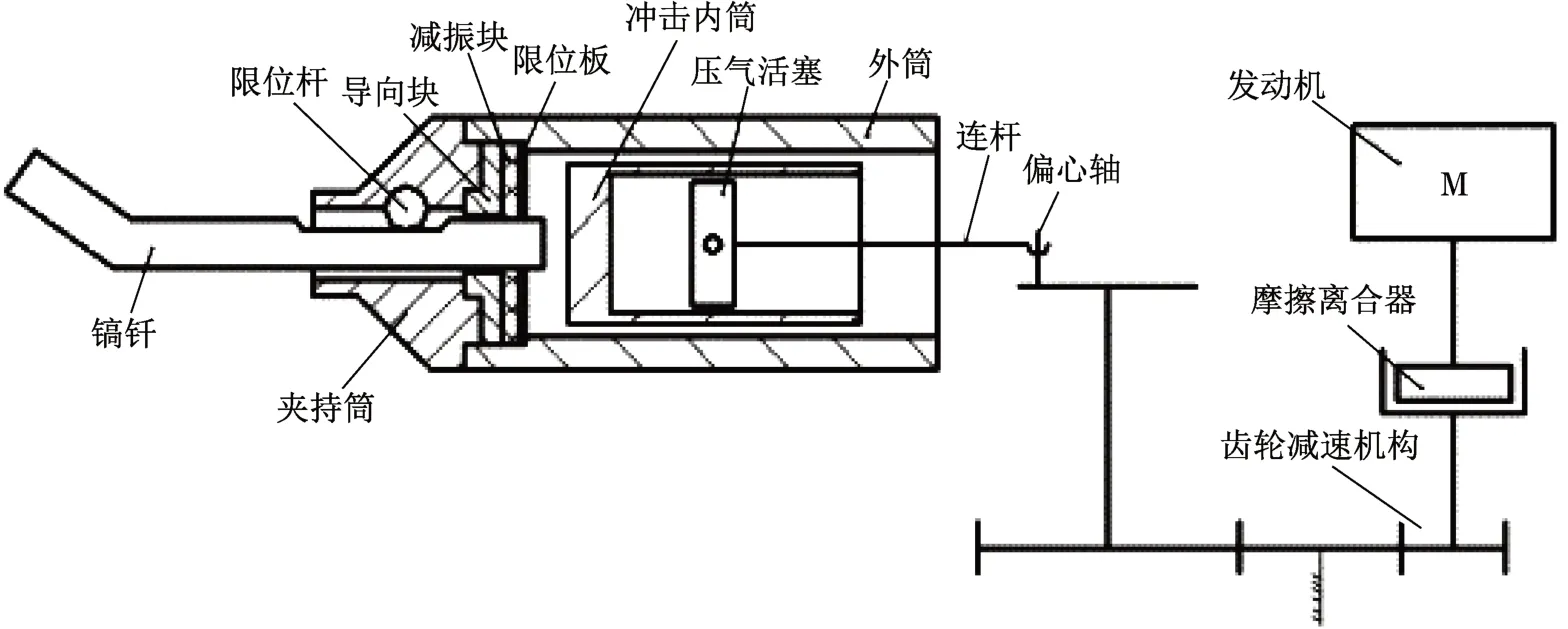
图1 捣固镐结构简图Fig.1 Structure of tamping pick

冲击系统是机具连续输出冲击能的核心，承受着周期性变化压强所产生的作用力，机具在捣固作业时，冲击频率较高，一般为770～1 800 r/min，对冲击系统零件的强度、疲劳寿命等有着较高的要求。冲击系统主要零件包括冲击内筒和压气活塞，由于冲击内筒结构相对简单，而压气活塞质量较小，承受交变载荷容易产生疲劳破坏，以压气活塞为研究对象，使用三维建模软件将模型导入ANSYS平台进行分析。

2 代理模型及修正

2.1 Kriging模型

Kriging模型是一种基于估计方差最小的线性回归技术，包含了非参数部分和线性回归部分，模型假设系统的响应值与自变量之间的真实关系可以表示成如下形式：

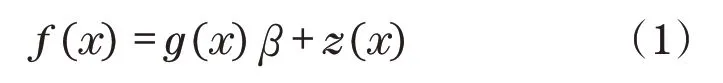
式中：g（x）为符合全局函数期望的线性回归函数，是Kriging模型的确定性成分，称为确定性漂移，且满足E［g（x）］=g（x）；z（x）为高斯随机函数，称为涨落。

其期望、方差及协方差为

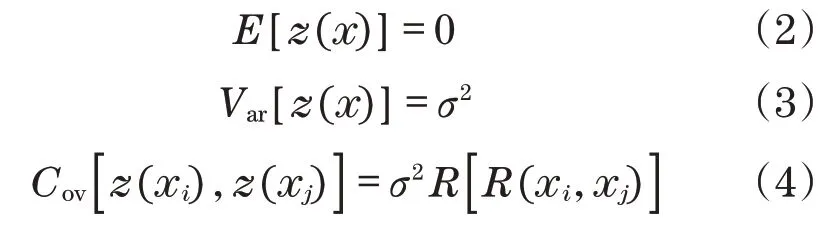
式中：R(xi，xj)为样本点xi和xj的相关函数，通常采用高斯函数。

为了获得响应面的最佳估计，所建立的模型应满足式（2），并同时使式（3）中的方差达到最小［8］。

假设建立f(x)的估计式为

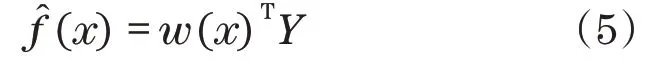
式中：w=(w1，w2，…，wn)T为待求权系数向量；Y=(y1，y2，…，yn)T为已知的样本点数据。

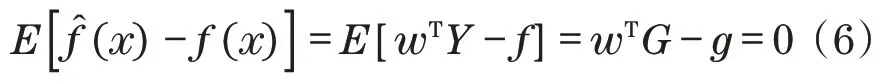
式中：G=(g(x1)，g(x2)，…，g(xn))T。

式（6）可以转换为

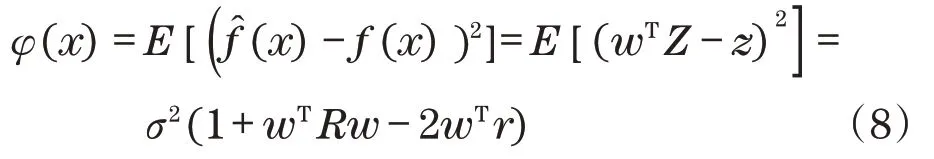
式 中：R=[Rij]=[R(c，xi，xj)]，(i，j=1，2，…，n)；r=(R(c，x，x1)，…，R(c，x，xn))T，R(c，x，xi)是使用核函数为高斯函数的相关函数，

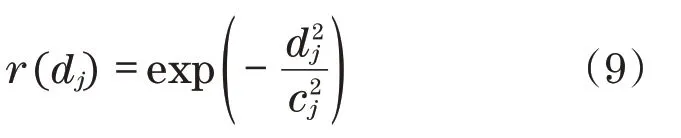
式中：dj为表征待测点与样本点间的距离关系；cj为核函数在样本点第j个方向的常数参量，各个方向上取值可以相同，也可以不同，此处取dj=|xj-|，(j=i，…，m；i=1，2，…，n)，其中，xj为待测点在第j个方向的坐标，为第i个样本点在该方向的坐标［9］。

由于Kriging响应面模型要求预测方差达到最小，所以求解式（5）中权系数w的问题最后转化为求解式（8）在式（7）的等式约束下的极值问题。求解得到最终结果如下：

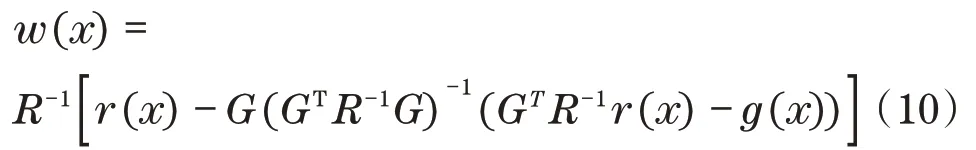
将其代回式（5）得

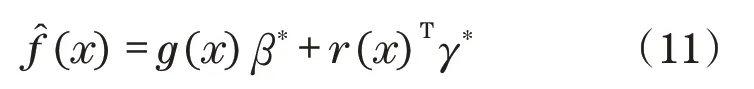
2.2 模型建立及修正方法

基于响应面的优化方法能够将具体的结构转化为数学模型，该模型是按照一定的方法抽样获取数据样本建立起来的，即试验设计（Design of Experiment，DOE）。试验设计是在整个设计空间中选取有限个试验点，通过合理布置试验点的位置，使其能够利用少量数据就能得到较高精度的响应面。目前常用的试验设计方法包括中心复合试验设计（Central Composite Design，CCD）、拉丁超立方试验设计（Latin Hypercube Sampling Design，LHS）以及最优空间填充设计（Optimal Space-Filling Design，OSF）等。这些方法都能按照一定的方式获取数学样本，但具有不同的特点。最优空间填充设计在整个空间内均匀分布，允许用户指定设计点数，具有更好的空间填充能力，且较适用于后续的Kriging响应面模型。模型修正的基本思路是在全局以及局部最大误差区域加入样本点，将响应面全局精度检验点、局部误差较大区域加密点和最优解样本点作为修正Kriging模型的数据，更新代理模型以确保最优解的精度满足要求，通过这些样本点的修正，能够提高模型全局寻优能力，避免在寻优过程中陷入局部最优的伪最优解，基本流程如图2所示。

图2 Kriging模型优化设计流程Fig.2 Kriging model optimization design process

具体步骤如下：

步骤1基于最优空间填充抽样获取样本点建立Kriging响应面。

步骤2检验Kriging响应面精度，若不满足精度要求，插入检验点和局部误差较大区域加密点修正响应面，再次检验响应面精度，直到满足要求为止。

步骤3根据已建立的响应面，使用多目标遗传算法求解最佳设计参数。

步骤4检验最佳设计参数处的响应面精度，若最佳设计参数处的响应面精度不满足精度要求，则重复进行步骤2～4，直到满足精度要求为止。

3 捣固镐优化设计

3.1 参数选择

因为压气活塞的外圆面要与冲击内筒配合，所以压气活塞的外圆尺寸已经确定，不具有优化空间。因此，压气活塞主要优化结构分布在前端凸台以及活塞内部。参数化尺寸选取如图3所示，表1列出了参数的变化范围。利用有限元软件获取样本点，将零件质量、活塞疲劳寿命及活塞最大变形等作为输出参数。

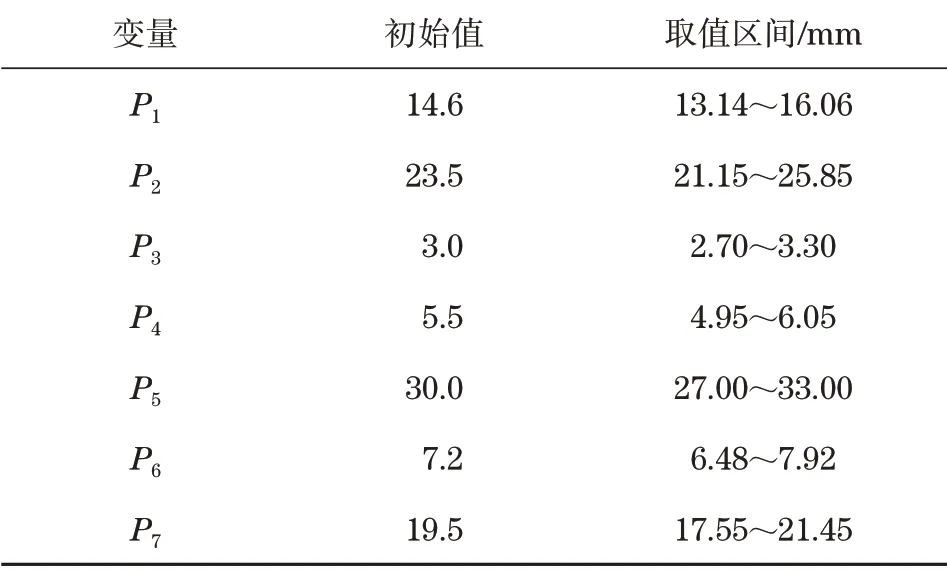
表1 各个参数变化范围Tab.1 Variation range of each parameter

图3 初始输入参数Fig.3 Initial input parameters

使用采样比较均匀的最优空间填充设计抽样方法，7个初始参数对输出参数的灵敏度如图4所示。

对图4分析可知，某些输入参数对输出变量影响不大，可在后续分析中省略。选择对零件质量P8、疲劳寿命P9和最大等效应力P10都有较大影响的输入参数，因此，选择关键参数为P1、P2、P4、P7、P8、P9和P10。

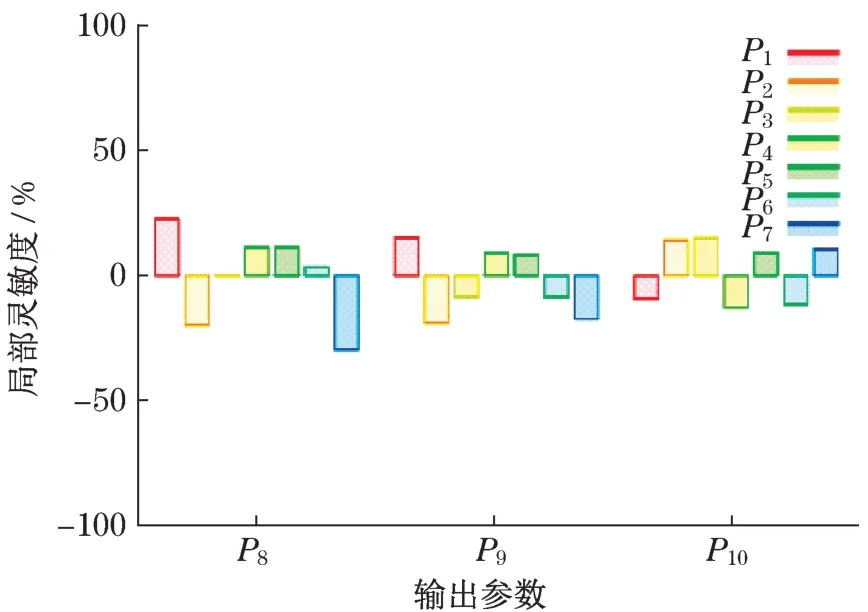
图4 灵敏度示意图Fig.4 Sensitivity diagram

3.2 优化模型构建

内燃捣固镐稳定运行时，压气活塞的冲击频率约为1 500 r/min，利用仿真软件［10］测得压气活塞与冲击内筒的运动速度及工作腔作用力如图5和图6所示。

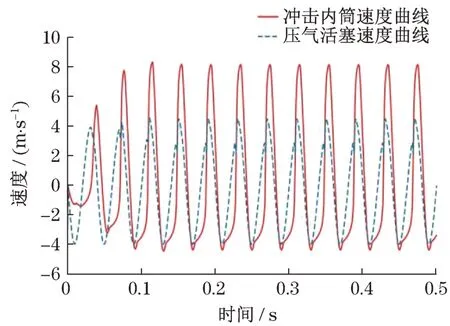
图5 冲击内筒与压气活塞速度曲线对比Fig.5 Speed contrast between impact inner cylinder and compressor piston

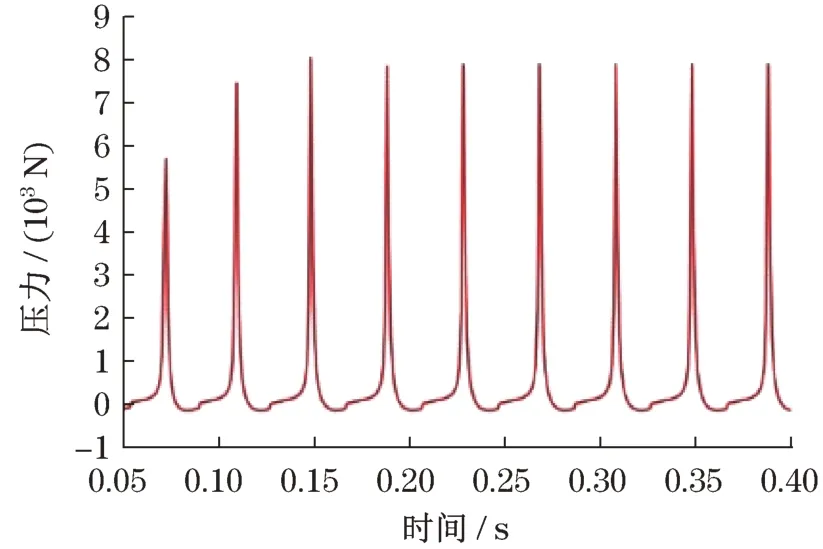
图6 工作腔压力曲线Fig.6 Force of cylinder working chamber

利用该仿真结果计算得出，捣固镐在该频率下的理论输出冲击能为56.42 J，与产品实际值55 J存在一定误差，但误差仅为2.59%，故仿真结果具备较高的可信度。使用该仿真结果作为压气活塞的外在条件。活塞所受压力变化频率高，虽然零件所承受的最大应力值远低于零件的屈服极限，但长期在高频周期性变化应力的作用下，也容易发生疲劳破坏。此外，该型捣固镐使用说明书中明确规定：捣固镐累计作业100 h后，应由专业人员进行检修，更换易损配件。其中，易损配件包括有压气活塞，因此，将零件疲劳寿命以及最大等效应力定为约束条件，将零件质量优化定为设计目标。建立优化模型如下：

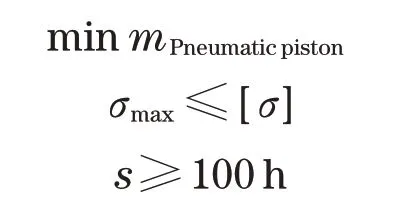
式中：σ为零件应力；s为零件使用寿命。其中，影响各指标的设计变量在规定的取值空间内变化，构建的优化模型通过多目标遗传算法求解。

3.3 优化求解与结果分析

利用最优空间填充设计抽样方法，在设计域空间抽取初始样本点集，基于该点集采用高斯相关函数构建Kriging响应面。通过相对最大绝对误差和均方误差对模型精度进行更新，直到满足精度要求再进入下一步骤。图7为迭代前后响应面模型对样本点和验证点的拟合图。

图7 迭代前后精度对比Fig.7 Precision comparison before and after iteration

对比图7（a）、图7（b）发现，经过多次迭代更新后的拟合效果较好，基本满足响应面精度要求。基于多目标遗传算法搜索3个最优解如表2所示，综合对比知方案2疲劳寿命最高，故将其作为最终的优化结果。取P1=15.1，P2=23.9，P4=5.3，P7=20.3，代入原模型分析，模型最大等效应力从56.3 MPa降低至53.9 MPa，降低了4.26%；模型疲劳寿命从原来的465 h提升到519 h，提高了11.6%。

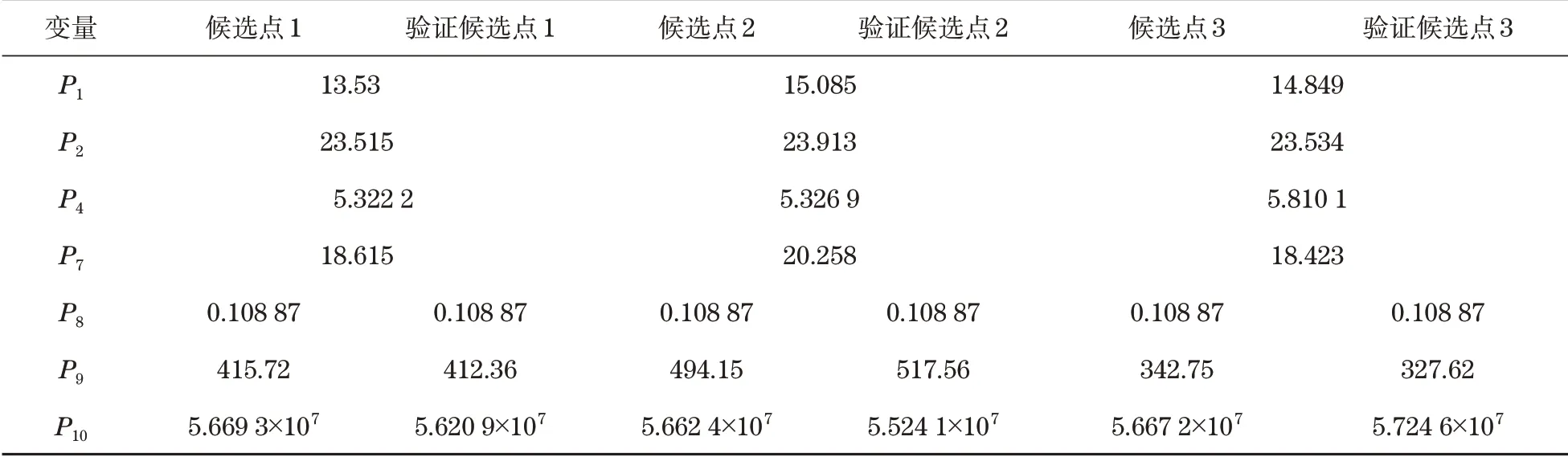
表2 方案及验证Tab.2 Scheme and verification

方案2的应力、疲劳寿命如图8和图9所示。

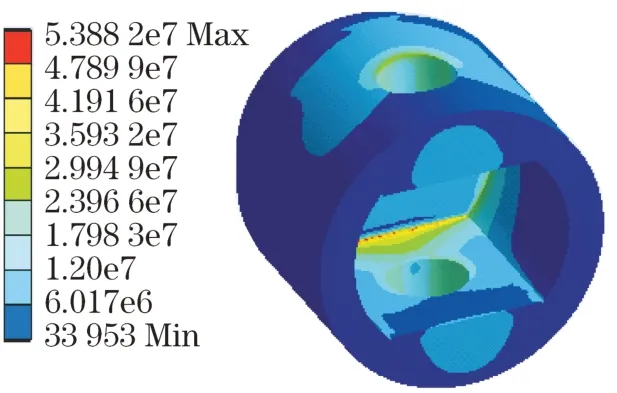
图8 等效应力云图Fig.8 Equivalent force nephogram

图9 疲劳寿命云图Fig.9 Fatigue life nephogram

4 结论

（1）区别于直接使用Kriging响应面模型进行结构优化，该方法基于最优空间填充设计，运用全局区域优化以及近似最优解局部加密处理等更新思想，建立了在全局空间和局部位置都具有较高精度的Kriging模型。在此基础上，基于多目标遗传算法得到优化问题的3个Pareto最优解，并根据不同的侧重点得到了最优参数。

（2）内燃捣固镐作为一种高频冲击设备，通过分析其物理结构及工作原理，建立仿真模型，经过上述方法的优化设计，所获得的压气活塞模型在满足强度、刚度的前提下，虽然质量未减小，但疲劳寿命有明显提高，也达到优化设计的目标。

（3）经过上述实例表明，该方法具有一定的实用价值，可为该类型产品的设计优化提供理论参考。