一种矿用变频器异步电动机参数离线辨识方法

蒋德智， 荣相， 陈雯雅， 王越， 连超

(1.中煤科工集团常州研究院有限公司，江苏 常州 213015；2.天地(常州)自动化股份有限公司，江苏 常州 213015)

0 引言

矿用变频器广泛应用于煤矿企业采、掘、运、通等过程，其性能优劣直接关系到煤机装备的安全稳定运行[1-2]。在无速度传感器条件下，变频器调速性能与异步电动机参数密切相关，而电动机厂家提供的铭牌参数仅表现了电动机的外部特性，因此，需要基于变频器逆变电路获取电动机内部参数[3-4]。

异步电动机参数辨识方法可分为在线辨识和离线辨识。离线辨识是在电动机投入运行之前，在电动机静止及空载状态下预先辨识参数。在线辨识是在电动机运行状态下进行参数测量和计算[5-6]。在线辨识依赖于离线辨识获得的电动机初始模型，且负载的扰动影响辨识准确性，因此,仅作为离线辨识的补充，在实际应用中仍需针对不同负载进行不断验证和改进[7-8]。离线辨识采用瞬态响应法测量漏感和转子电阻，采用稳态响应法测量定子电阻、自感和互感，避免了负载扰动的影响，是目前矿用变频器产品采用的主要参数辨识方式。目前对离线辨识方法的研究不断完善，如考虑铁损、电流的趋肤效应、死区时间、逆变电路器件压降及非线性特性等影响[9-10]，然而，现有方法大多采用快速傅里叶变换等计算电流幅值和相位，存在频谱泄漏和栅栏效应，易导致测量误差。

针对上述问题，本文基于两电平三相逆变电路，将电动机等效电路作为负载，用PWM(脉冲宽度调制)信号控制IGBT(绝缘栅双极型晶体管)，从而控制负载端激励电压，通过电流传感器检测定子电流，计算定子电阻、转子电阻、定转子互感、漏感等参数，实现异步电动机参数离线辨识。

1 异步电动机等效电路

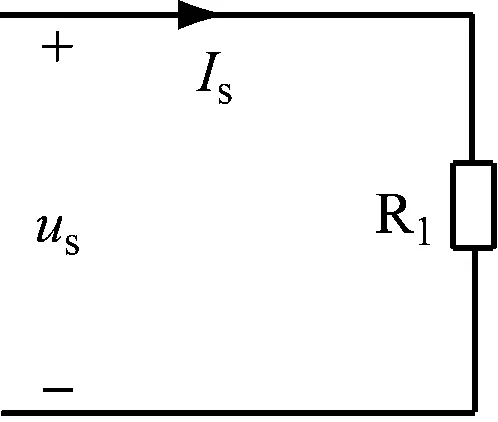
异步电动机一相绕组等效电路如图1所示，其中us为定子电压，R1为定子电阻，Lσ1为定子漏感，Lσ2为转子漏感，R2为转子电阻，Lm为定转子互感，s为转差率。该等效电路将转子侧参数折算到定子侧[11]。电动机参数辨识在该等效电路的基础上实现。

图1 异步电动机一相绕组等效电路

2 异步电动机参数辨识方法

2.1 定子电阻辨识方法

基于稳态响应法，通过直流试验进行定子电阻辨识。通过PWM信号控制逆变电路，在任意一相与另外一相或两相绕组之间施加一定的等效直流电压，检测绕组电流，计算出定子电阻[12]。当两相之间施加直流电压时，定转子互感、漏感相当于被短接，单相等效电路和实测时的两相等效电路如图2所示。其中uuv为U相和V相之间施加的定子电压,Is为定子电流，Ru，Rv，Rw为三相等效定子电阻。测试期间W相上下桥臂一直处于关断状态，W相定子电阻处于悬空状态。

(a)单相等效电路

当直流电压施加到定子侧时，相当于直流母线电压udc经过逆变器开关器件和定子电阻形成回路[13]。U相和V相之间施加的电压uuv波形如图3所示，其中t为时间，D为占空比，ta为调制载波周期。在0～Dta时间段内，U相上桥臂导通、下桥臂关断，V相上桥臂关断、下桥臂导通，uuv=udc；在Dta～ta时间段内，U相上桥臂关断、下桥臂导通，V相上桥臂导通、下桥臂关断，uuv=-udc。

图3 定子电阻辨识过程中的电动机电压波形

由图3可知，输出等效直流电压u满足如下关系：

udcDta+(1-D)ta(-udc)=uta

(1)

u=(2D-1)udc

(2)

结合图2和式(2)可得

u=IsR1

(3)

(4)

通过控制PWM信号的占空比调节输出电压，从而调节定子电流。由式(2)可知，若占空比D由50%开始向上调节，则输出等效直流电压由0开始增大，电动机电流随之逐渐增大。在Matlab/Simulink仿真环境下，按照上述方法在定子侧施加直流电压并调节，得到定子电流响应波形，如图4所示。可见,稳态时U相电流和V相电流大小相等、极性相反。

图4 定子电阻辨识过程中的电流响应波形

为了保证异步电动机的安全，同时使定子电流在可准确测量的范围内，调节等效直流电压，使电动机定子电流分别达到100%，150%电动机额定电流。设定子电流达到100%电动机额定电流时的占空比为D1，使占空比固定不变，多次采样直流母线电压并求取平均值udc1，多次采样电动机定子电流并求取平均值i1。同理可得定子电流达到150%电动机额定电流时对应的占空比D2、直流母线电压平均值udc2、电动机定子电流平均值i2。将2次输出电压差值与2次电流差值的比值作为实际的定子电阻值：

(5)

与采用单次采样值直接计算的方式相比，采用2次采样值差值计算的方式可减小因逆变器IGBT器件压降引起的测量误差[3]。

2.2 转子电阻和漏感辨识方法

2.2.1 方法原理

由图1可知，当通入角频率为ω的交流电压时，互感抗为

ZLm=ωLm

(6)

当通入方波阶跃电压时，理想状态下，阶跃瞬间电压交流分量角频率ω为无穷大，则互感抗ZLm为无穷大，此时电动机单相等效电路如图5(a)所示。控制逆变电路U相上桥臂IGBT器件开通和关断，V相和W相下桥臂IGBT器件始终处于开通状态，此时电动机等效电路如图5(b)所示。互感相当于开路，因此,电动机没有电磁转矩，与堵转的情况相同。此时定转子漏感之和为Lσ=Lσ1+Lσ2，定转子电阻之和为R=R1+R2，则电动机三相阻抗Zu，Zv，Zw为

(a)单相等效电路

Zu=Zv=Zw=R+jωLσ

(7)

由图5可知，在等效电路中，单相总阻抗Z的电压uz为

(8)

由式(7)和式(8)可得

(9)

式中：iu为施加电压后等效电路中的直流电流，取2次电流测量值的平均值；Δiu为施加电压后等效电路中的电流变化量，取2次电流测量值的差值；id为施加的电压断开后等效电路中的直流电流，取2次电流测量值的平均值；Δid为施加的电压断开后等效电路中的电流变化量，取2次电流测量值的差值。

通常认为定转子漏感相等，则有

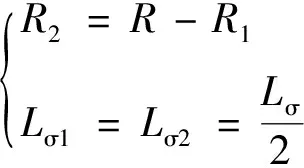
(10)

式(9)中，udc可通过仿真环境获得，占空比D和载波周期ta可由仿真调节过程得到。进行转子电阻和漏感辨识时，每次发出N个PWM波，获得2N个采样电流值In,n为采样次数。根据采样电流值可求得Δiu，Δid，iu，id：

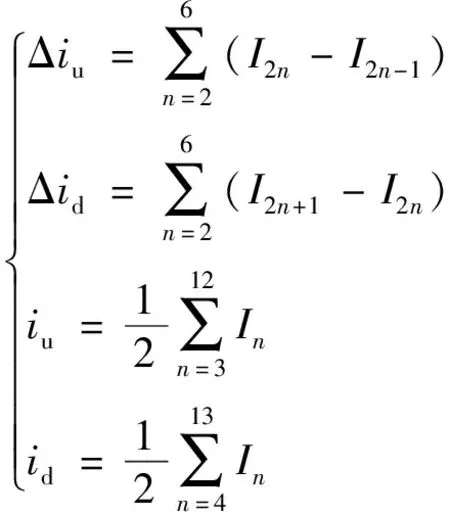
(11)

将式(11)代入式(9)、式(10)，求得1组转子电阻和漏感。求取多组转子电阻和漏感，去掉最大值和最小值，求平均值，得到最终的转子电阻和漏感。

2.2.2 仿真验证

通过Matlab/Simulink平台对上述方法进行仿真验证。异步电动机模型参数如下：电动机功率P=2.2 kW，额定电压为380 V，定子电阻R1=3.92 Ω，定转子漏感Lσ1=Lσ2=11.90 mH，互感Lm=215.87 mH，转子电阻R2=1.52 Ω。

仿真时，控制器连续按组发出PWM波，每组7个脉冲。在电感储能作用下，每组第7个脉冲发出时，电动机电流达到峰值。调节占空比，使电流峰值达到电动机额定电流后，保持占空比恒定，对电压、电流进行采样并计算转子电阻和漏感。占空比恒定后，定子电压波形和电流响应波形如图6所示。

(a)电压波形

转子电阻和漏感辨识的1组仿真采样数据见表1，一共获取6组数据，每组14次采样，组与组之间间隔80 ms。结合采样数据，通过转子电阻和漏感辨识方法求得转子电阻R2≈1.50 Ω，定子漏感Lσ1≈11.80 mH，与Matlab/Simulink给定的电动机模型参数相符，验证了转子电阻和漏感辨识方法的准确性。

表1 转子电阻和漏感辨识仿真采样数据

2.3 定转子互感辨识方法

进行三相异步电动机恒压频比空载实验时，电动机转速接近同步转速，转差率s近似等于0，转子电流近似等于0，可认为转子侧开路。定转子互感辨识等效电路如图7所示[14]。

图7 定转子互感辨识等效电路

三相异步电动机通入三相交流电压信号，使异步电动机在额定频率下旋转。等效电路中互感Lm和定子总电感L、定子漏感Lσ1的关系为

Lm=L-Lσ1

(12)

在恒压频比模式下，逆变电路通过SVPWM调制输出三相对称的等效正弦电压，电动机定子将产生旋转磁场，因此与同步旋转坐标系下的异步电动机模型相符[15]。根据图7可得到M-T同步旋转坐标系下的异步电动机电压、电流如图8所示,其中ISM,IST分别为定子电流矢量Is在M轴、T轴方向的分量。

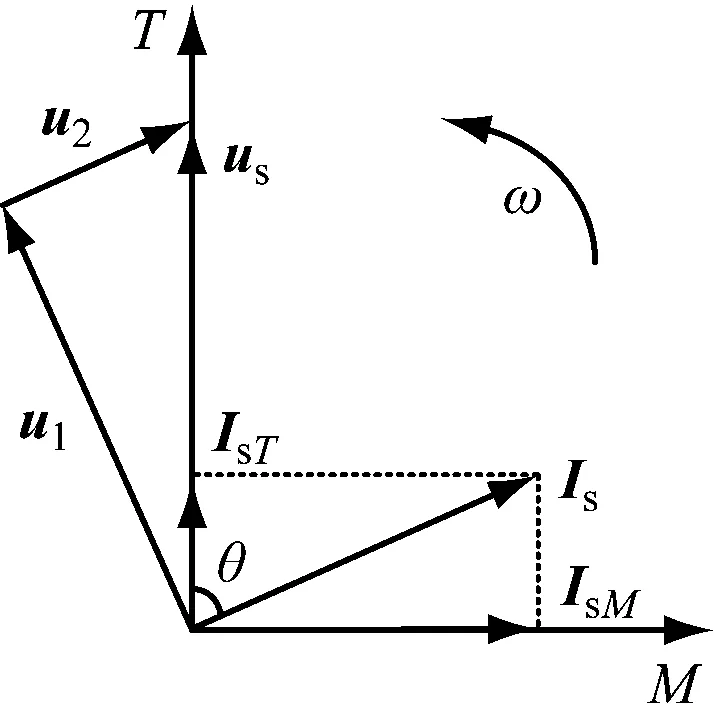
图8 同步旋转坐标系下异步电动机电压、电流相量图

M-T坐标系和电压矢量us以正弦信号角频率ω旋转，若取T轴参考方向与电压矢量us参考方向相同，将电压矢量us分解为平行于Is的电压矢量u2和垂直于Is的电压矢量u1，则有

(13)

式中θ为功率因数角。

空载电流Is为空载状态下采样的定子电流信号，由式(13)可得电动机定子总电感：

(14)

在计算出漏感数据的基础上，结合式(12)，可求得异步电动机定转子互感Lm。

3 电动机参数辨识结果验证

3.1 电动机参数辨识实验

一般实验室采用市电供电，由于电源容量所限，验证平台上的电动机功率为2.2 kW，因此，前期验证采用380 V/2.2 kW三相异步电动机。搭建380 V/2.2 kW变频器机芯，对参数辨识方法的准确性进行初步验证。

2.2 kW电动机参数辨识过程中的电压波形如图9所示。定子电流采用2 000∶1霍尔电流传感器测量，通过400 Ω采样电阻上的分压来反映。定子电压采用高压差分衰减探头直接测量,示波器已经调整探头衰减比例,图中定子电压幅值为实际值。

(a)定子电阻辨识波形

在异步电动机参数辨识过程中，变频器施加给电动机的电压信号得到了正确的电流响应，与仿真结果一致。

实测2.2 kW电动机完整参数见表2。由偏差情况可知，测量过程可重复性较好，辨识结果是收敛的。

表2 实测2.2 kW电动机完整参数

3.2 电动机参数辨识和变频器控制效果

搭建660 V/90 kW矿用变频器机芯，采用本文提出的参数辨识方法进行参数辨识，将辨识出的电动机参数输入变频器矢量控制软件，验证能否达到整机性能指标要求。矿用变频器机芯和性能测试平台如图10所示。

(a)矿用变频器机芯

实测90 kW电动机完整参数见表3。将该参数作为矢量控制算法的常量，用于电流解耦和励磁、转矩闭环控制。

表3 实测90 kW电动机完整参数

变频器控制电动机在100%额定转矩下带载启动并达到稳定运行状态，电动机转速、转矩、输出频率和电流波形如图11所示。转矩、转速通过加载系统的转矩、转速传感器测量，输出频率、电流通过电能质量分析仪测量。电动机启动成功后持续输出额定转矩并运行30 min，变频器加速到额定转速的时间为30 s，为了体现带载启动时的低频转矩输出能力，仅记录前32 s启动过程。为了观测方便，将输出频率曲线放大10倍显示。由图11可知，将辨识出的电动机参数用于矿用变频器矢量控制系统，变频器能够在额定转矩下带载启动并持续稳定运行。

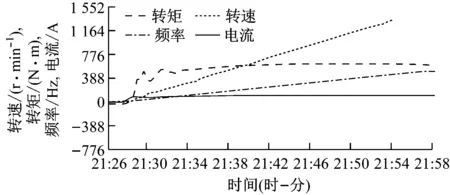
图11 电动机转速、转矩、输出频率和电流波形

4 结论

(1)基于稳态响应法，通过直流试验进行定子电阻辨识。采用2次采样值差值计算的方式得到定子电阻，与采用单次采样值直接计算的方式相比，可减小因逆变器IGBT器件压降引起的测量误差。

(2)采用瞬态响应法辨识转子电阻和漏感，Matlab/Simulink仿真结果表明，转子电阻和漏感参数辨识结果与给定的电动机模型参数相符，验证了参数辨识方法的准确性。

(3)建立同步旋转坐标系下的电动机模型，在恒压频比空载运行状态下，对电流瞬时值进行旋转坐标变换，计算电流幅值和相位，进而辨识定转子互感和空载励磁电流。

(4)实验及测试结果表明，电动机参数辨识过程可重复性较好，辨识精度较高，可满足矿用变频器矢量控制要求。