基于Hilbert-Huang变换的抗冰导管架平台损伤识别研究

王铭基，孙珊珊，谢孜源，王延林

（1.大连理工大学运载工程与力学学部，辽宁大连 116024；2.大连理工大学海洋科学与技术学院，辽宁盘锦 124221；3.大连理工大学物理学院，辽宁盘锦 124221）

0 引 言

海洋石油平台远离陆地，其一旦发生意外，不但会造成巨大的经济损失及人员伤亡，而且还将对海洋环境造成灾难性的破坏，因此海洋石油平台的安全问题尤为重要。寒区海上油气开发中，海冰对油气开发设施的破坏能力要远远高于波浪、海流、风等其它常规环境荷载。冰荷载是冰区海洋结构设计与使用过程中需要重点考虑的外荷载，是冰与结构作用发生破碎而产生的[1]。海冰与柔性导管架平台作用会引起导管架结构的冰激振动问题，冰振进而会引起平台主体结构以及上部设备与管线的疲劳破坏，同时会影响平台上部工作人员的舒适度，降低工作效率[2]。寒区抗冰导管架平台在服役期间受到海冰的长期作业，动冰荷载会使结构产生疲劳损伤问题。同时波浪荷载、风荷载、环境的腐蚀等其他环境荷载长期积累也会引起结构不同程度的损伤问题。这种损伤往往是隐性的，需要定期对结构进行检测，以保证结构的安全。传统的损伤检测方法主要有声波法、超声波法、磁场检测法、X 射线检测法和电涡流检测法等[3]。但导管架平台是一个复杂的大尺度的结构物，利用传统的检测方法不但效率低且实时性差。当结构发生损伤时，结构的刚度、强度、阻尼等结构特征参数会发生改变，从而使结构响应的时域、频域、时频域特征发生改变，所以可以通过监测到的结构冰激振动响应实现对结构的损伤识别、定量和定位。冰荷载引起的结构振动响应相对于风、波浪等常规载荷要大一个甚至几个量级，是十分容易监测到的，因此更易通过响应进行损伤识别。这种方法相对于传统的结构检测方法效率高，且可以实现对损伤的长期实时监测。

海冰与导管架平台作用是一个随机过程[4]，得到的结构响应是一个非线性非平稳的信号。常见的振动响应信号处理方法包括傅里叶变换和小波变换，但是这两种信号处理方法都具有一定的局限性。傅里叶变换是把信号展开为一系列三角函数的和，代表信号的全局性质，难以捕捉突变的信号。小波变换的信号分析结果依赖于小波基函数的选取。HHT（Hilbert-Huang Transform）是一种针对非线性非平稳信号的处理方法[5]，其可以根据信号的特点自适应地产生固有模态函数，并不受测不准原理制约，适合突变信号，可以较好地分析信号的瞬时特性，被广泛应用于地震信号分析[6]、海洋结构损伤检测[7]中。

本文应用HHT 方法对结构振动响应信号进行分析和处理，通过结构损伤前后Hilbert边际能量谱的变化构建损伤指标，利用该指标对JZ20-2MUQ 平台模型进行损伤识别，通过对有限元仿真得到的响应数据的分析处理，实现冰荷载作用下的抗冰导管架平台模型的损伤识别，并探讨海冰的冰速、冰厚对该损伤指标的影响，探究利用HHT对抗冰导管架平台进行损伤识别的可行性。

1 基于Hilbert-Huang 变换的响应信号的损伤特征量的构造

1.1 经验模态分解（EMD）

Hilbert-Huang 变换包含两部分，第一部分为经验模态分解（EMD），它是由Huang 提出的；第二部分为Hilbert谱分析（HAS）。HHT处理非线性非平稳信号的基本过程是：首先利用EMD 方法将给定的信号分解为若干固有模态函（IMF），这些IMF是满足一定条件的分量；然后，对每一个IMF进行Hilbert变换，并表示在时频域中，联合这些变换结果得到信号的时频特征；最后，利用信号的时频特征进行损伤特征量的构造。

经验模态分解（EMD）方法的实质是通过特征时间尺度来识别信号中所内含的所有振动模态。其分解出的固有模态函数（IMF）是根据信号本身特性决定的。EMD 分解方法是基于以下假设条件：数据至少有两个极值，一个最大值和一个最小值；数据的局部时域特性是由极值点间的时间尺度唯一确定；如果数据没有极值点但有拐点，则可以通过对数据微分一次或多次求得极值，然后再通过积分来获得分解结果。

EMD 方法的分解过程其实是一个数据选择的过程，这个数据选择过程依据信号特点自适应地把一个复杂信号分解为一列固有模态函数（IMF）。它满足如下两个条件：信号极值点的数量与零点数相等或相差是一；信号由极大值定义的上包络和由极小值定义的下包络的局部均值为零。

其数据选择过程如下：

1.2 Hilbert变换

对信号经过经验模态分解（EMD）得到的每一阶固有模态函数（IMF）ci(t)进行Hilbert变换，对信号进行卷积，即

基于此变换，建立解析函数zi，并得到信号的瞬时幅值ai和瞬时相位函数φi：

瞬时频率ωi定义为瞬时相位φi对时间t的导数：

信号x(t)被表示为

在这里忽略了原始信号的残差部分rn，Re代表级数展开的实部部分，把上述公式的右边部分叫做Hilbert谱，即

将式（9）与时间积分得到的希尔伯特边际谱为

将H(w,t)的平方对时间积分得到的希尔伯特能量边际谱为

希尔伯特边际谱代表对应信号的瞬时频率波动的幅值分布，希尔伯特能量边际谱代表对应信号的瞬时频率波动的能量分布，两种谱均具有很高的时频分辨率，对损伤前后信号的变化十分敏感。

1.3 基于响应信号的损伤特征量的构造

当结构产生损伤时，结构的特征参数（刚度、阻尼）会发生改变，同时这些改变会影响结构的响应，海洋结构的响应信息主要包括位移、倾角、振动加速度等。抗冰导管架平台的桩腿在振动时可以看作一个多自由度系统，当桩腿发生微小损伤时，特别是在海冰荷载这种较大的激励时，其损伤位置周围测点的结构响应会比平时剧烈，这时的结构响应信息肯定会比平时更有利于损伤的检测。所以我们可以利用结构的响应信息对抗冰导管架平台进行损伤识别，利用Hilbert-Huang 变换对结构损伤前后的希尔伯特能量边际谱进行比较。相比于边际谱中的信号振幅，希尔伯特能量边际谱可以将因结构损伤产生的信号能量变化放大。对于像海洋平台这种大尺度结构，有利于对结构很微小损伤的识别。因此基于希尔伯特能量边际谱，定义信号的能量变化DI为

式中，Eh(ωi)和Ed(ωi)分别为健康的海洋结构和损伤的海洋结构的信号在各时刻的希尔伯特能量边际谱值。通过式（12）可以看出，当DI值为0 时，结构响应信号希尔伯特能量边际谱前后没有变化，表明结构没有损伤；而当DI值大于0时，说明结构响应信号在各频带上会发生变化，DI值越大，说明和健康结构的响应信号能量差异越大，说明结构损伤越大。因此，利用响应信号的希尔伯特能量边际谱变化量可以判断结构是否有损伤发生。

2 损伤指标的仿真分析

2.1 结构参数

本文选取的平台原型是位于渤海海域辽东湾北部的JZ20-2MUQ 平台，其为4 桩腿加锥的抗冰导管架结构。该平台所处海域设计水深为15.6 m，平台水上部分高为39 m，水下部分为17 m，4 个桩腿间距为14 m，桩腿本身有5°左右斜度，桩腿直径约1.5 m。平台整体质量为2 700 t，其中自重约1 000 t，上部结构等效质量约1 700 t。桩腿水面位置装有抗冰锥体，锥体斜面为60°，锥体交界处的最大锥径为4 m。本文通过ANSYS 建立有限元模型，平台为钢结构，杨氏模量为200 GPa，材料密度为7 800 kg/m3，泊松比为0.3，利用MASS21单元模拟上部质量，利用Pipe20 单元模拟桩腿的水上和水下部分，利用Beam188单元来模拟导管架中的斜撑部分，导管架底部约束采用6 倍桩径法[8]，不考虑桩土的相互作用，结构阻尼比为0.025。抗冰导管架平台有限元模型如图1所示。

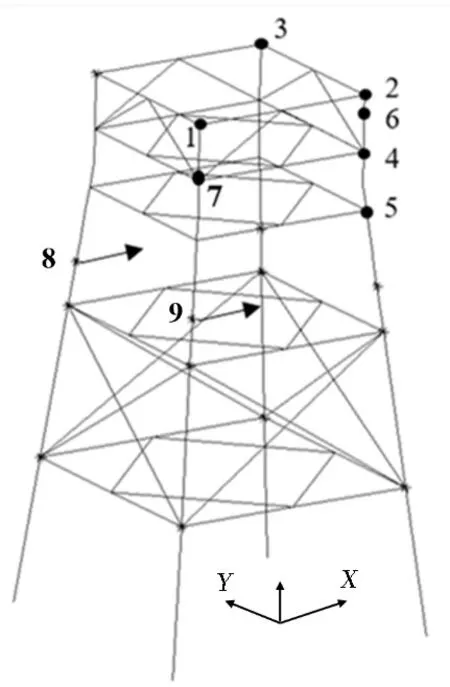
图1 抗冰导管架平台的有限元模型Fig.1 Finite element model of ice-resistant jacket platform

2.2 结构冰荷载

寒区海上油气开发过程中，海冰对油气开发设施的破坏能力要远远高于其它常规环境荷载。海冰与锥体的作用是一个周期性过程，由于海冰与锥体结构作用的特殊性，海冰会在加载一段时间后断裂，会发生加载和卸载循环的状态。针对锥体结构的冰荷载，可以采用岳前进等[9]根据大量现场实测数据得到的锥体的确定性冰力函数来计算，如图2所示。用公式可以表达为

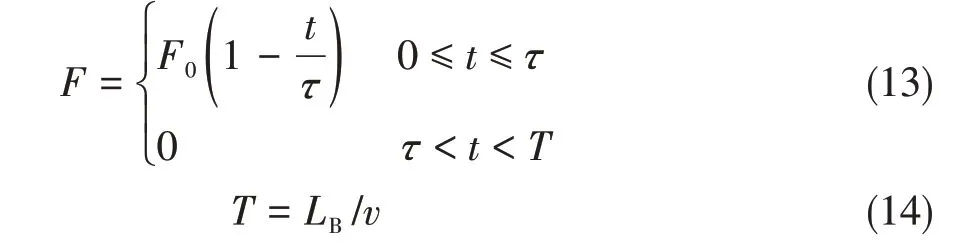
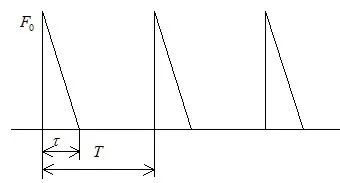
图2 确定性冰力函数Fig.2 Determined ice force function

式中：F0为锥体结构极值静冰力，可近似等于锥体水平冰力FH；T为冰力周期，τ取冰力周期T的1/3；LB为冰板的破碎长度，一般取7倍的冰厚[10]；v为海冰速度，单位为m/s。

针对锥体结构的极值静冰力计算，我们采用Hirayama-Obara 冰力计算模型[11]的弯曲破坏项对现场试验得到的冰力数据进行修正[12]。选取这一公式的主要原因是在Hirayama-Obara 的室内试验中，结构形式与渤海的锥体比较接近。由于我们分析的锥体较窄，冰力公式中只包括冰的弯曲破碎分量。Hirayama-Obara给出的冰力弯曲破碎分量计算公式为

式中：B为待定系数，渤海取3.7；σf为冰的弯曲强度，取渤海辽东湾设计值700 kPa；h是冰的厚度，单位为m；D为冰作用处锥体直径，取4 m；E为海冰弹性模量，单位为Pa；ρw为海水密度，单位为kg/m3；g代表重力加速度，单位为m/s2，ν为海冰的泊松比。

在仿真分析中，把对应工况下冰力时程进行离散化处理并导入ANSYS 中形成插值形式的冰力时程曲线，冰力正向（沿着X方向）作用于平台两个桩腿的入水点处（节点8、9），由于考虑屏蔽效应，因此只作用于两个桩腿。

2.3 损伤指标分析

为了研究本文构建的损伤指标对损伤识别的效果，本文在荷载和损伤位置不变的情况下，比较不同损伤程度时损伤指标的变化情况。常用的模拟损伤的方法有：改变壁厚和减小杨氏模量。本文采用减小壁厚来模拟损伤，损伤位置为图1 中的点6，是长为0.1 m 的单元，设置七种损伤情况来对损伤指标进行分析，详见表1。首先对导管架平台模型进行模态分析，选取结构一阶平动和一阶扭转自振频率计算得到结构瑞利阻尼系数为：α=0.143 0，β=0.004 4。因为结构的损伤相对结构整体而言很微小，所以可以认为结构的瑞利阻尼系数是不变的。利用2.2 节中的理论，把冰荷载输入到ANSYS 中，其中海冰的厚度为20 cm，速度为0.5 m/s，冰荷载正向作用于平台两个桩腿（沿着X方向），加载的时程为10 个冰力周期，利用ANSYS 瞬态动力学分析对结构模型进行动力响应分析，由于冰荷载作用于X方向，所以结构的主要动力响应都发生在X方向上。在真实的结构监测过程中，传感器往往布置在海洋平台的每一层甲板上，同时为了研究损伤的定位，我们选定平台的1、2、3、4、5、7点作为测点，上述测点测量的均是结构在X方向上的振动加速度，采样频率为100 Hz，分析损伤指标的敏感程度，以及纵向、横向的定位能力。分析得到结构各测点的振动加速度响应信号后，选取平稳数据段对其进行Hilbert-Huang 变换，并计算各个工况下损伤指标DI值。下面以6 点处未发生损伤和6 点处损伤35%（损伤情况7）两种状态下测点2 的振动加速度响应值为例，说明对信号进行Hilbert-Huang 变换和计算DI值的过程。

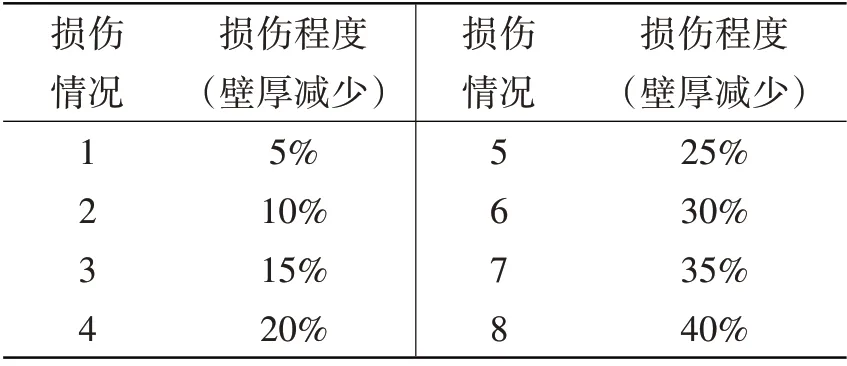
表1 损伤程度Tab.1 Damage degree

把测点2 输出的加速度响应时程信号导入MATLAB 对其进行经验模态分解。图3 和图4 分别显示了健康和损伤35%（损伤情况7）状态下，测点2处原始响应信号及其经验模态分解（EMD）的结果。

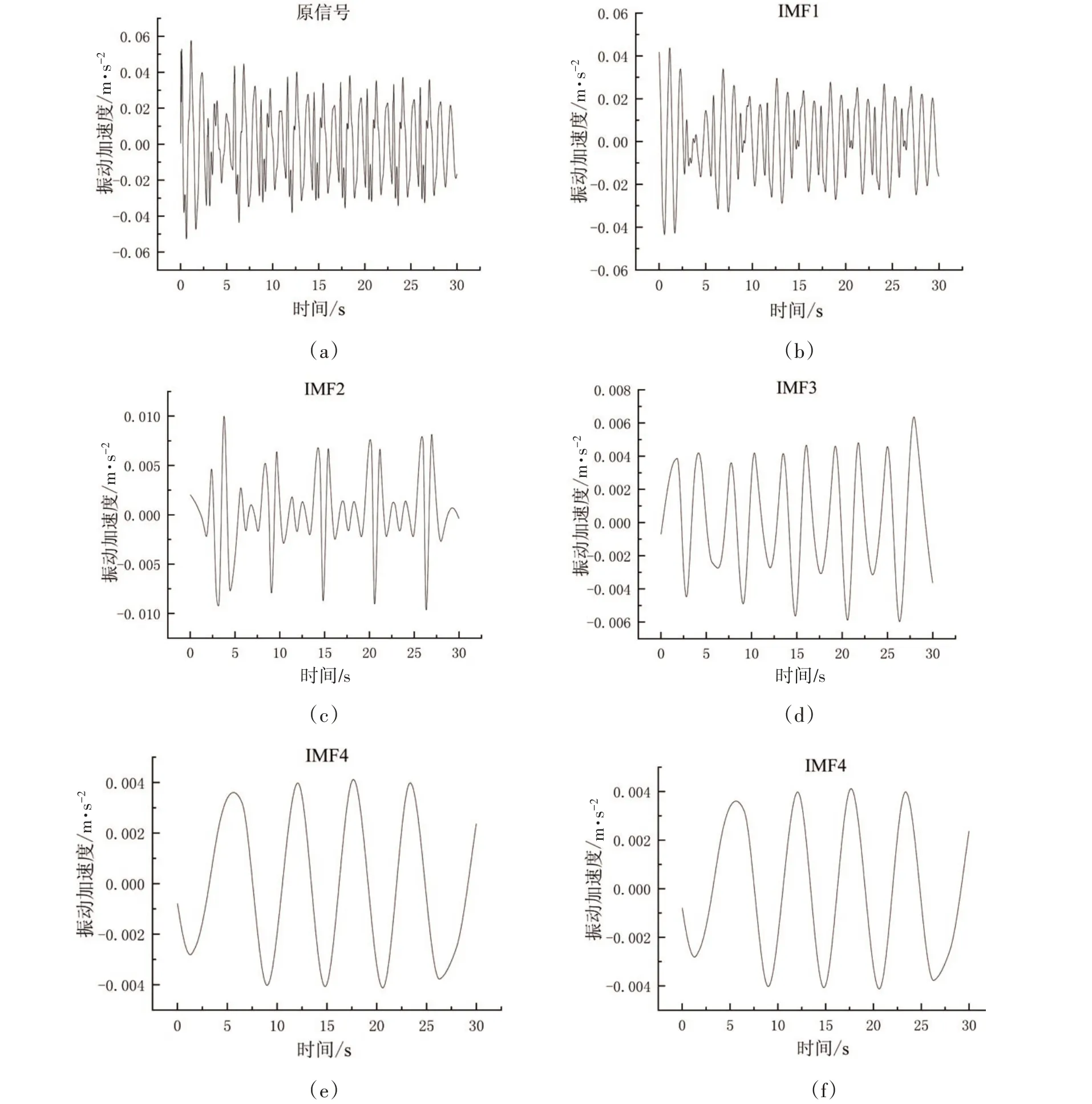
图3 健康状况下原始信号与EMD分解的结果Fig.3 Results of original signal and EMD decomposition in healthy condition

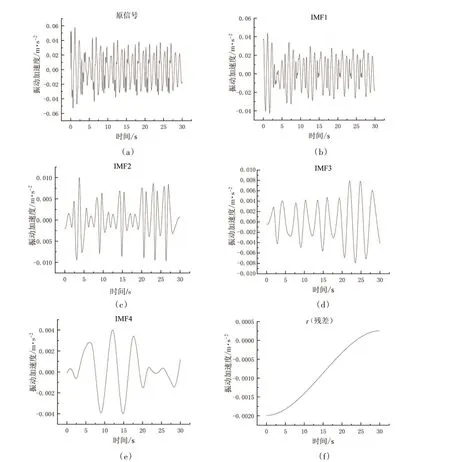
图4 损伤情况7下原始信号与EMD分解的结果Fig.4 Results of original signal and EMD decomposition under Damage Condition 7

通过对各阶IMF 分量进行Hilbert 变换得到信号的Hilbert 谱，其频率分辨率为0.01 Hz。对Hilbert谱在时域内先平方再积分得到信号的Hilbert能量边际谱，Hilbert能量边际谱显示了信号在0～2.5 Hz频率范围内的能量分布。图5（a）和图5（b）分别为点6处未发生损伤和点6处损伤35%（损伤情况7）两种状态下测点2 的Hilbert 能量边际谱，可以看出信号的频率成分主要集中在1 Hz 左右，与结构水平方向低阶自振频率相符。

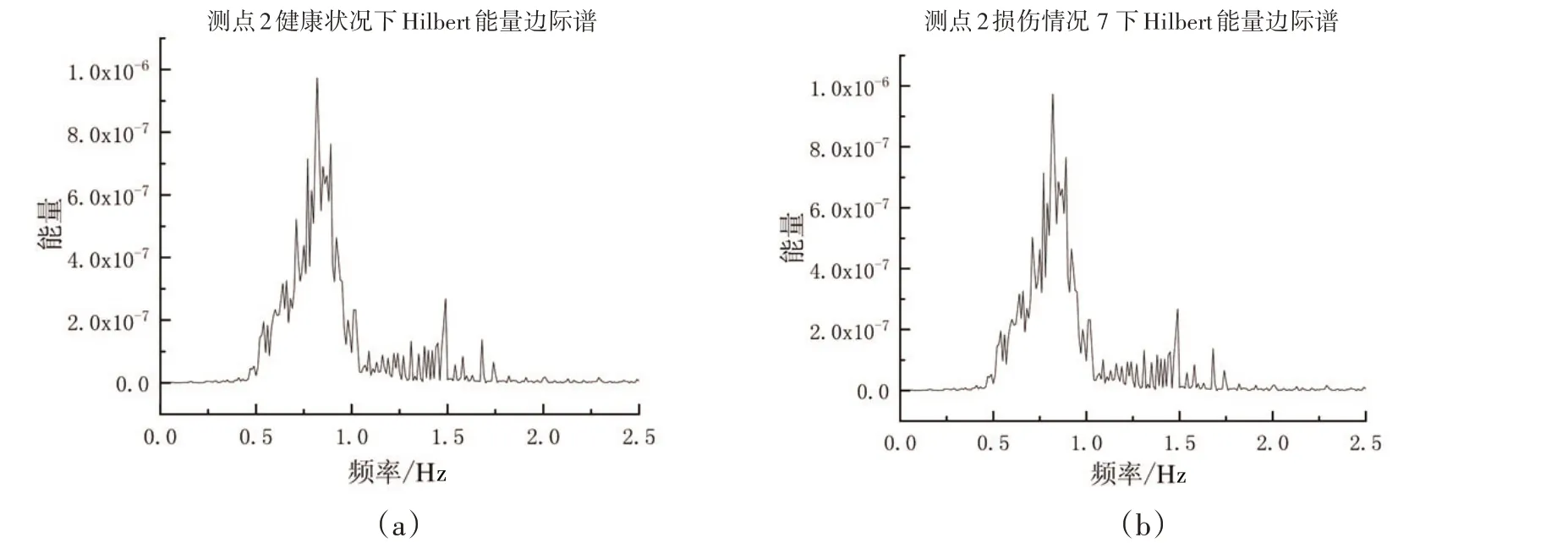
图5 两种情况下Hilbert能量边际谱Fig.5 Hilbert energy marginal spectra in two conditions

由式（12）计算得到在损伤情况7 下测点2 处损伤指标DI值为0.006 6，与健康状态相比有很大变化。对各种损伤情况下每个测点的响应信号均按上述过程分析处理，得到DI值如图6～7 所示。从图中可以看出，损伤指标与损伤位置和损伤程度成正相关关系，其表现出的规律如下：

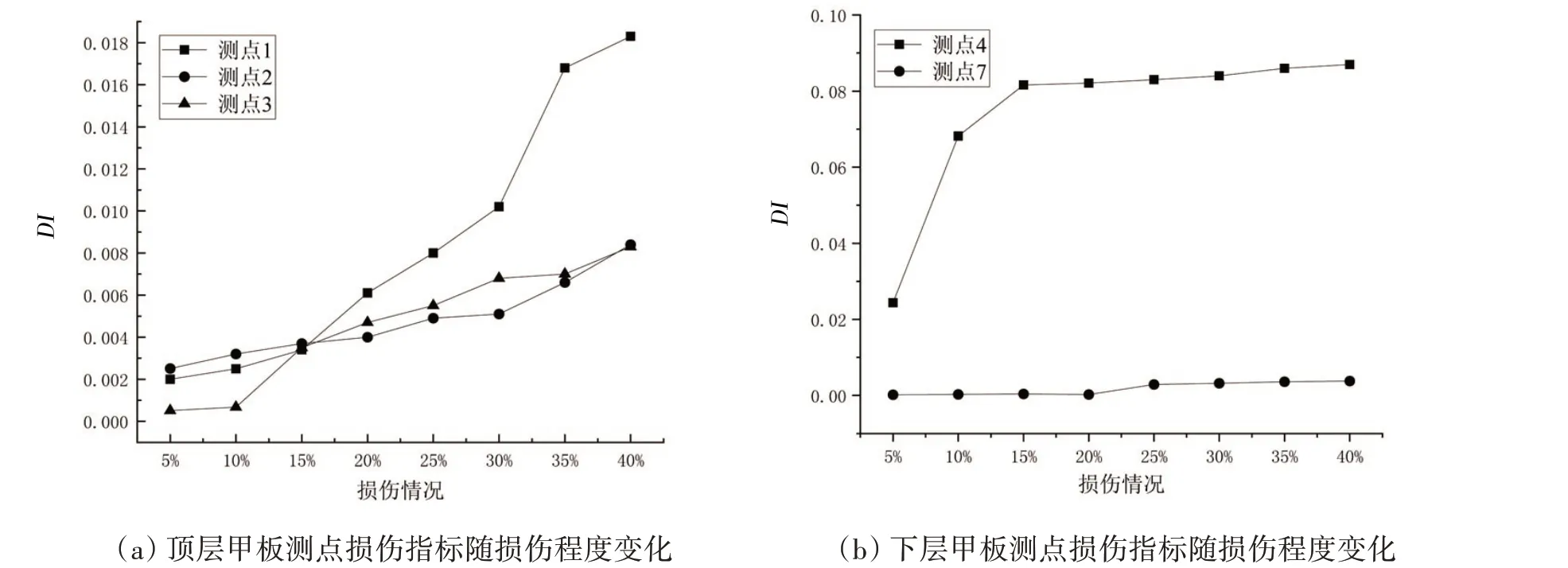
图6 同层甲板测点损伤指标随损伤情况变化Fig.6 Damage index of the monitoring points changing with damage degree on same deck

（1）如图6（a）所示，在冰荷载作用下，顶层甲板随着损伤位置的损伤程度的增加，当损伤比较小的时候，靠近损伤位置6点的测点2损伤指标DI值比较大，当损伤比较大时，靠近冰荷载冲击的测点1 的损伤指标DI值变化更明显。如图6（b）所示，下层甲板测点7的损伤指标DI值始终远小于靠近损伤位置6 点的测点4，在结构监测的过程中可以选择海冰漂流方向顶层甲板布置传感器，去评估损伤程度，选择下层甲板布置传感器，可以识别出损伤横向位置。

（2）如图7 所示，在冰荷载作用下，不同层甲板随着损伤位置的损伤程度的增加，远离损伤位置的测点5的损伤指标DI值始终小于靠近损伤位置6点的测点2和4，可以识别出损伤纵向位置。

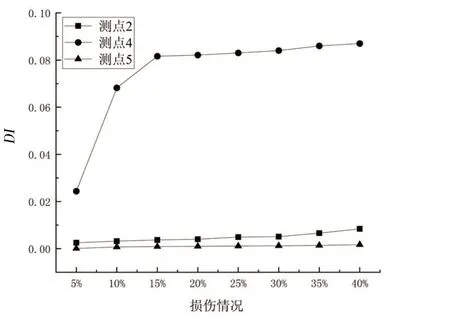
图7 不同层甲板测点损伤指标随损伤程度变化Fig.7 Damage index of monitoring points changing with damage degree on different decks

（3）由损伤情况下各个测点的DI值可以看出，损伤位置一定（点6）时，随着损伤程度的增加，DI值变大，说明DI值与模型结构的损伤程度存在着正相关关系。

2.4 冰厚对损伤指标的影响

冰厚影响着冰荷载的极值大小，是最重要的海冰参数之一。保持冰速0.5 m/s、损伤位置（点6）、损伤程度（10%）不变，根据中国海海冰条件及应用规定[13]，此海洋平台所在海域最大冰厚为35 cm，所以改变冰厚分别为20 cm、25 cm、30 cm、35 cm，取10个周期计算各个测点处的损伤指标DI值，计算结果如图8所示。从图中可以看出，当冰层较厚时，由于激励频率降低，极值冰力的增大，上层甲板靠近海冰激励的测点1的DI值会有较大的变化，下层甲板靠近损伤位置的测点4的DI值会有较大的变化，对于不同层甲板测点2、4、5，靠近损伤位置的测点DI值始终大于远离损伤位置的点。所以，损伤指标在不同冰厚下均是有效的，可以明显识别出损伤位置。

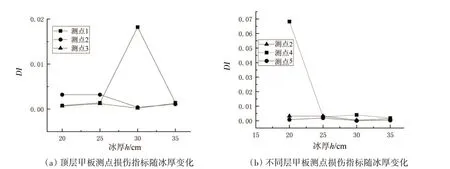
图8 测点损伤指标随冰厚变化Fig.8 Damage index of monitoring points changing with ice thickness

2.5 冰速对损伤指标的影响

冰速影响着冰荷载的频率，是最重要的海冰参数之一。保持冰厚20 cm、损伤位置（点6）、损伤程度（10%）不变，根据中国海海冰条件及应用规定[13]，此海洋平台所在海域平均冰速为0.4 m/s、最大冰速为1 m/s，改变冰速分别为0.4 m/s、0.6 m/s、0.8 m/s 和1 m/s，取10 个周期计算各个测点处的损伤指标DI值，计算结果如图9所示。从图中可以看出，随着冰速变快，激励频率的加快，其他测点损伤指标DI值影响不是很大，但是靠近损伤位置的测点4会有巨大变化，且对于不同层甲板测点2、4、5，靠近损伤位置的测点DI值始终大于远离损伤位置的点，所以损伤指标在不同冰速下均是有效的，可以明显识别出损伤位置。

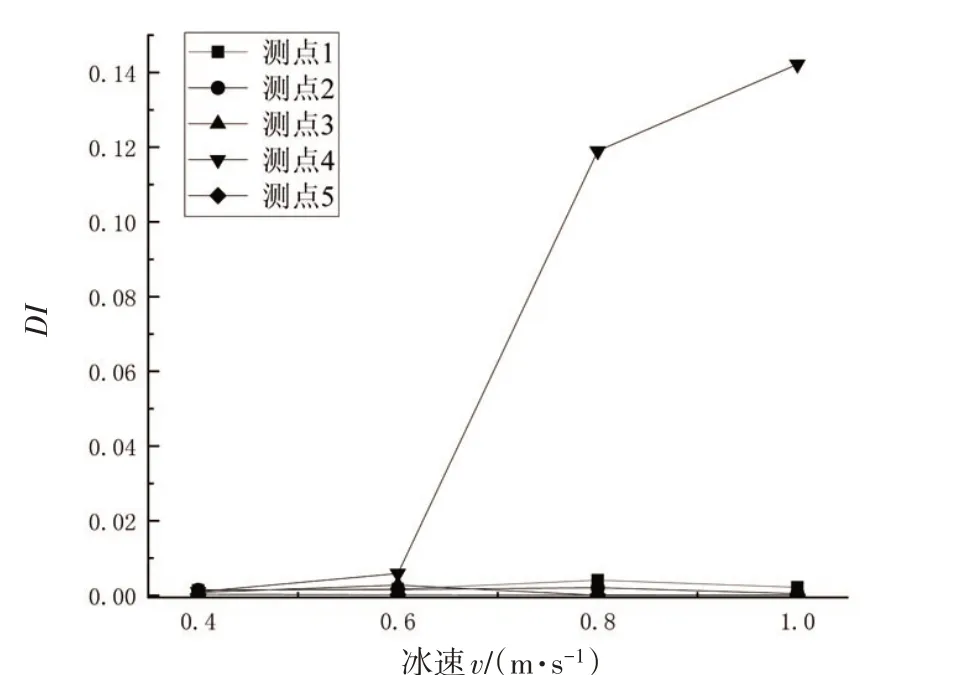
图9 测点损伤指标随冰速变化Fig.9 Damage index of monitoring points changing with ice velocity

3 结 论

本文应用Hilbert-Huang 变换对抗冰导管架平台有限元模型损伤前后的振动加速度响应信号进行了分析，探讨了损伤程度、海冰参数对该损伤指标的影响，得到了以下结论：

（1）当结构某部位发生损伤时，激励力作用下得到的结构各测点的振动响应信号的模态成分都会发生变化，顶层甲板靠近海冰激励的位置测点随损伤程度的变化损伤指标变化更加明显，从而实现损伤程度的识别。损伤位置下层甲板横向测点和不同层甲板测点之间距离损伤部位较近的测点DI值比较大，DI值可以表征靠近损伤位置和远离损伤部位的差异，从而实现损伤位置的识别。不同损伤程度、海冰厚度和海冰速度下该指标的有效性不受影响。

（2）在同一损伤位置，随着损伤程度的增加，损伤指标DI值相应变大，DI值与模型的损伤程度存在着正相关关系。

（3）损伤指标在不同冰厚、冰速下均是有效的，可以明显识别出损伤位置。海冰厚度的改变对损伤前后能量边际谱的影响主要集中在损伤位置周围和受到海冰激励方向的上层甲板测点，会使损伤指标有较大的波动。海冰速度对损伤位置下层甲板的DI值的影响十分明显，当冰速比较大时，损伤位置下层甲板的DI值远远高于其他测点的，当冰速较大时，更有利于此方法对损伤的识别定位。

基于响应信号Hilbert能量边际谱构造的损伤指标DI值能够实现结构损伤的定位识别，并能根据其大小对损伤严重程度进行定性判断，相比于传统方法更加方便简单，但对于损伤程度和位置的更准确的识别，还需进一步改进优化算法。