波浪冲洗对多浮冰耦合运动影响特性研究

朱仁庆，张 曦，李志富

（江苏科技大学船舶与海洋工程学院，江苏镇江 212001）

0 引 言

有证据表明北极地区海冰覆盖面积随着全球气候变化整体呈现出减小趋势，使得北极航线的开通和自然资源的大规模开发成为可能[1]。冰缘区处于开阔水域和海冰的交界处，受波浪影响十分显著。掌握冰缘区内海冰与波浪相互作用的规律，对于正确认识冰区内波浪传播特性以及合理开发北极具有重要的指导意义。

现阶段研究波浪与海冰的相互作用主要采用模型试验和数值模拟的方法。在模型试验方面，Montiel等（2013）[2]开展了浮冰在波浪中运动的试验研究，并对理论预报结果与实测数据之间差别的可能来源进行了分析。Bennetts 和Williams（2015）[3]利用理论与试验相结合的方法，对波浪经冰区的传播规律进行了研究，并发现散射是造成波能衰减的主要原因。Bennetts等（2015）[4]通过试验研究发现，波浪透射能量一般随着入射波波陡的增加而减小，并且在入射波波长等于浮冰特征长度时达到最小极值。Yiew等（2016）[5]对规则波中浮冰的三自由度运动响应进行了试验分析，发现波浪冲洗现象可以明显抑制浮冰的运动响应。Yiew 等（2017）[6]利用试验研究了在不同波长和波高的规则波激励下两个薄圆盘的运动，并且基于Slope sliding 理论预测了圆盘的运动，其中浮冰只限于单一方向水平运动。在数值模拟方面，Susan等（2001）[7]实测了巴伦支海浮冰的六自由度运动响应，并通过谱分析方法研究了浮冰在不同波频下的幅值特征。Bennetts 和Squire（2009）[8]建立了冰缘区内波浪的三维散射模型，研究发现浮冰厚度，浮冰行对齐方式、行间距以及浮冰半径都对波浪的反射现象有影响。随后，Bennetts 等（2010）[9]利用冰缘区内的三维波浪散射模型预测了波浪衰减率，研究发现，波浪衰减与入射波角度呈指数关系，其中斜入射波衰减最快。浮冰形状、分布以及其吃水对波浪衰减的影响很小。Montiel等（2015）[10]给出了一种多个浮冰作用下的波浪散射模型，通过改变浮冰随机分布密度证明了单个浮冰是影响波浪散射的主要因素，仅需三个浮冰即可解释浮冰的多重散射效应。倪宝玉等（2019）[11]利用Fluent软件研究了多浮冰与波浪的相互作用，研究发现浮冰数目的增多抑制了浮冰运动，浮冰的存在一定程度上阻碍了波浪运动。

目前，对于波浪与多浮冰作用问题，尽管已有相关研究，但是有关多浮冰耦合运动过程中的波浪冲洗效应研究还十分有限。基于此，本文建立了二维粘流数值水池，模拟了波浪作用下多浮冰的耦合运动，并重点对比研究了不同浮冰数目条件下波浪冲洗冰体表面现象对浮冰垂荡、纵摇运动的影响规律。

1 数值计算方法

1.1 控制方程

为了有效计及湍流影响，在求解流体控制方程时将控制方程中的各项分解为时间平均值和相对于这些平均值的脉动值两部分，即雷诺时均方程组，其表达式如下：

1.2 数值造波理论

本文采用速度入口造波方式完成造波任务，在入口处采用松弛区域消波技术，以消除浮冰引起的波浪反射对造波的影响；出口处采取阻尼消波方法来达到消波目的。本文选取斯托克斯五阶波[12]，以精确模拟冰体上浪等非线性现象。在造波边界处的速度和波面瞬时升高满足以下条件：

x方向速度为

z方向速度为

波面瞬时升高为

式中各系数如下：

其中，ω、d和k分别为圆频率、水深和波数。定义c=coshkd、s=sinhkd，其余各项系数参见文献[13]。

在入口处采取松弛区域消波方法，通过在动量方程中添加源项qϕ使得波浪在近速度入口时逐渐变为入射波，源项表达式如下：

式中：γ为强迫系数，其中γ= -γ0cos2( πx*/2 )，它使得在指定入口消波区内强迫消波的力度逐渐变大；ϕ为数值模拟计算出的动量输运方程的结果；ϕ*为原动量方程的理论解。

在出口处应用阻尼消波的方法，通过在波浪运动的垂直方向添加阻尼实现消波，其阻尼项表达为

为适应未来城市化加速发展、工业化深化发展、土地、耕地和水等资源日益短缺、国内人口流动规模不断加大、国际游客不断增多等的态势，新世纪我国养猪业将朝着优质、高效、安全的目标发展，养猪生产将以适度规模化、规范化、标准化、生态循环经济模式为主体，多项技术的综合配套利用是提高养猪业整体生产水平和效益的关键。下面将从育种、营养、猪肉安全生产等方面探讨我国新世纪养猪业的发展。

式中：xsd为消波区起始位置的坐标；xed为消波区结束位置的坐标；f1、f2、nd为阻尼消波模型的参数；w为坐标轴z方向的速度。

1.3 浮体运动方程

在随浮体进行平移和旋转的运动坐标系中，浮体的运动方程为

式中，m为浮体质量，I为浮体转动惯量，f为流体施加于浮体的合外力，M为浮体受到的合外力矩。

2 算例设置

2.1 二维模型和网格划分

本文选用RKE 2L湍流模型[14]来对控制方程进行封闭求解。离散方法选用有限体积法，采用PIMPLE 算法将压力速度进行耦合。采用VOF 法对自由液面进行捕捉。如图1所示，水池左边界、上边界以及下边界设置为速度入口条件；前后两侧边界设置为对称边界条件；右侧边界设置为压力出口条件。入口消波区和出口消波区长度分别取为一个波长长度。

图1 流域边界Fig.1 Sketch of the computational domain

计算区域长10.5 m、高0.8 m，水深0.5 m。在水池中加入浮冰模型，如图2 所示，处于中间位置的浮冰放置于距离入口4.25 m 处。位于中间浮冰的位置不变，在中间浮冰两侧以对称的方式逐渐增加浮冰数目，其中相邻浮冰中心间隔0.75 m。本文中的浮冰运动被视为刚体运动。如图3所示，浮冰模型采用了两种简化模型，浮冰模型长为0.5 m，冰厚为0.05 m，浮冰密度为600 kg/m3，入水深度为0.03 m。为了防止流体冲洗冰体表面，在圆柱上表面增加了一圈薄护栏，护栏高度为0.05 m，理论研究表明添加护栏对浮冰运动的影响可忽略不计[4]。波浪参数设置如表1所示。

表1 波浪参数Tab.1 Wave parameters

图2 二维数值水池Fig.2 Two-dimensional numerical wave tank

图3 二维浮冰模型Fig.3 The geometry of two-dimensional ice floes

本文采用动网格技术来模拟浮冰运动。为了精确地模拟浮冰以及波浪运动，在数值水池中对自由液面区域进行加密，并且对浮冰运动区域也进行了网格加密。图4为工况2的网格示意图。

图4 动网格示意图Fig.4 Diagram of the dynamic mesh method

2.2 网格及时间步收敛性分析

结合极地冰缘区历史波高和周期的概率分布，以及波浪参数（见表1）与浮冰直径的无量纲比例关系，在给定波浪要素的前提下，研究不同浮冰数目条件下的冰体耦合运动，其中波长为1 m，波高为0.04 m。

选择数值水池中处于中间浮冰所在位置作为液面升高探测点，选取给定的入射波波浪要素来记录该点处液面升高时历，与斯托克斯五阶波理论解进行对比。对于波幅（A）较小的波浪来说，沿着波高（H）方向的网格大小（Δx）对造波效果起着决定性作用。因此，本文选取自由液面波高方向三组不同网格大小，设置不同时间步（Δt）来对造波效果进行收敛性分析，波高方向网格大小分别为Δx=H/5，Δx=H/10，Δx=H/15。同时，沿波长方向的网格分布与波高方向网格分布之比为4:1。具体网格与时间步设置如表2所示。

表2 网格与时间步设置Tab.2 Settings of grid size and time step

3 计算结果及分析

浮冰在波浪中的耦合运动与浮冰之间的分布形式密切相关。为了进一步探索浮冰与入射波相互作用时，浮冰数目对耦合垂荡、纵摇运动响应的影响，本文对不同浮冰数目工况中处于中间位置的浮冰垂荡（η3）和纵摇（η5）运动响应进行了频谱分析。

3.1 遮蔽效应

为了消除波浪冲洗冰体表面的影响，通过模拟有护栏浮冰在波浪中的运动来分析其与波浪的相互作用。在研究中发现，当流体域中存在多个浮冰时，不同位置处的浮冰个体与波浪的相互作用存在差异。位于前侧的浮冰阻碍了波浪的运动，使得位于后侧的浮冰与波浪的相互作用较弱。

图7 是工况3 的一个周期内运动示意图，位于前侧的浮冰与波浪发生了较强的相互作用，表现出较剧烈的摇荡运动。位于后侧的浮冰运动状态相较于前侧的浮冰，其摇荡运动较小。同样地，后侧浮冰窄缝内的波浪运动相比于前侧浮冰窄缝内的波浪运动逐渐趋于平坦，波浪产生明显衰减。

图7 一个周期的浮冰运动Fig.7 Motion response of ice floes in one wave period

图8提取了各个工况中位于中间位置浮冰的垂荡和纵摇运动，在波浪激励频率下，图8（a）中浮冰的垂荡运动幅值随着浮冰数目的增多而减小。随着浮冰数目的增多，海冰对波浪的传播产生越来越严重的阻碍作用，使得波浪发生明显的耗散，浮冰接收到的波浪能量也因此发生很大程度的衰减，导致浮冰受到波浪的作用较小。随着浮冰个数的减小，波浪受到的传播阻碍变小，波浪传递给浮冰的能量变大，浮冰与波浪的相互作用变强，因此使得浮冰在波浪激励频率下的运动变大。同样地，图8（b）中，随着浮冰数目的增多，波浪激励作用对中间位置的浮冰纵摇运动影响变小，其纵摇幅值减小，纵摇运动的变化趋势与垂荡运动变化趋势相似。

图8 不同浮冰数目下有护栏浮冰运动幅值对比Fig.8 Motion amplitude of the middle ice floe with barrier at different ice floe numbers

因此，由上述分析可知，由于多浮冰与波浪的相互作用以及多浮冰的耦合效应，浮冰对波浪具有一定的遮蔽和衰减作用。随着浮冰数目的增多，位于中间位置的浮冰运动相应变小。浮冰窄缝距离波浪入口越远，窄缝间的波浪运动也趋于平缓。

3.2 波浪冲洗现象

在真实海况中，海冰受到波浪的作用会发生剧烈运动，并出现一定量的流体涌上冰体表面的现象。本文通过数值模拟发现，由于波浪冲洗现象的出现，无护栏浮冰运动与有护栏浮冰运动有明显差异。随着浮冰数目的增加，处于中间位置的浮冰受到的波浪冲洗程度也有减小。

图9 分别对应处于工况1 和工况5 中间位置浮冰冰表面所受到的波浪冲洗现象。图9（a）对应工况1，浮冰上表面明显被流体覆盖，并且入射波浪有再次冲洗的趋势，表现出较强的波浪冲洗现象；图9（b）对应工况5，浮冰上表面几乎没有流体覆盖，波浪相较于工况1 较平缓，没有呈现上浪趋势，相较于前者，工况5没有出现波浪冲洗现象。

图9 不同浮冰数目工况中波浪冲洗冰体表面过程Fig.9 Overwash phenomena at different ice floe numbers

图10中给出了工况2的浮冰垂荡、纵摇的频谱分析图。波浪激励频率下，无护栏浮冰的垂荡运动幅值小于有护栏浮冰垂荡运动幅值。在纵摇运动响应中，其与垂荡运动响应具有相同的趋势，无护栏浮冰在波浪激励频率处的运动幅值也远远小于有护栏浮冰。表3提取了各个工况中波浪激励频率下的浮冰运动幅值。经过对比发现，无护栏浮冰与有护栏浮冰出现幅值差异的原因主要是波浪冲洗冰体表面，堆积在冰体表面的水阻碍了浮冰的运动。

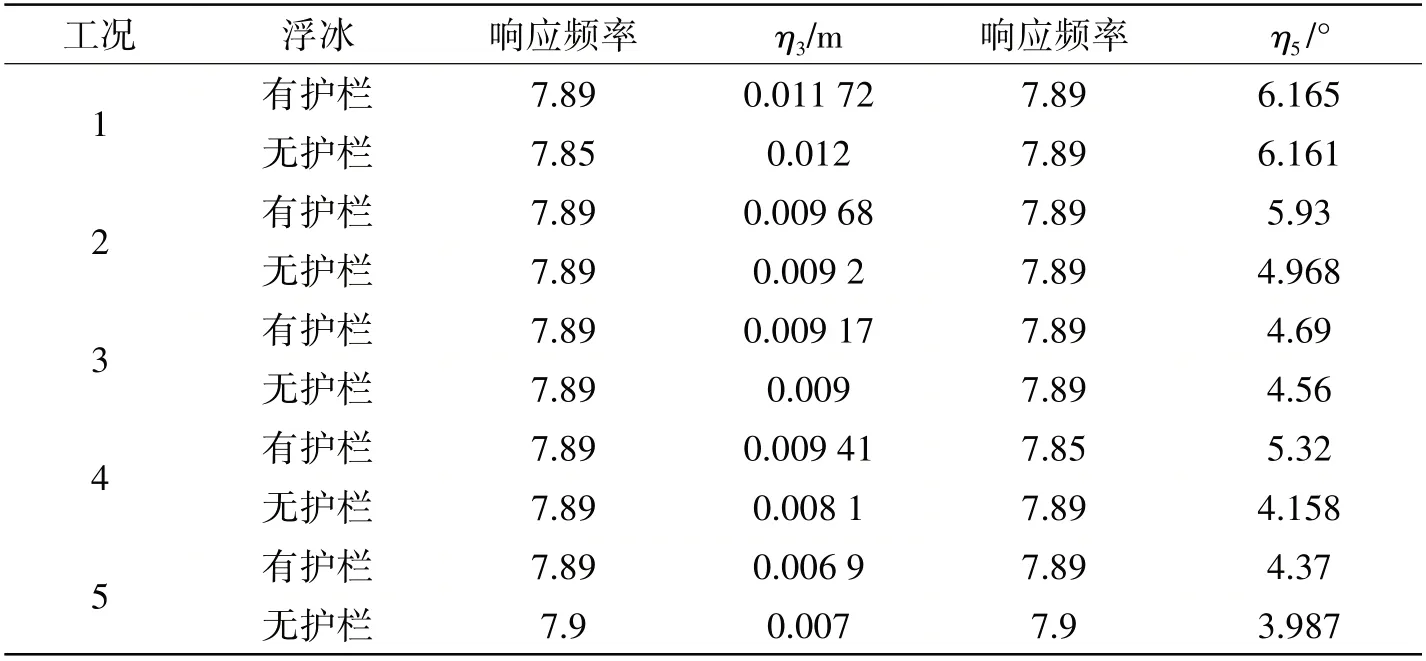
表3 中间浮冰运动幅值Tab.3 Motion amplitude of the middle ice floe

图10 工况2中间浮冰运动幅值对比Fig.10 Motion amplitude of the middle ice floe corresponding to Case 2

图11给出了工况1至工况5中位于中间位置无护栏浮冰的垂荡、纵摇运动响应频谱分析图，即不同浮冰数目工况中出现的波浪冲洗现象对中间位置浮冰运动的影响。由图11可知，随着浮冰数目的增加，浮冰对波浪的遮蔽作用以及衰减作用变强，中间位置浮冰接受到的波浪能量减少，导致波浪激励频率下浮冰的垂荡运动与纵摇运动减小。当浮冰数目较少时，由于存在较明显的波浪冲洗现象，浮冰运动幅值差异较大。随着浮冰数目的增多，波浪能量衰减较大，浮冰受到的波浪冲洗现象减小，浮冰运动幅值减小。

图11 不同浮冰数目对无护栏浮冰的运动响应影响Fig.11 Comparison of the motion amplitudes of the ice floe without barrier at different ice floe numbers

综上可知，无护栏浮冰由于受到波浪冲洗的作用，其运动幅值明显小于有护栏浮冰。同时，随着浮冰数目增加，中间浮冰受到的波浪冲洗现象减弱，该浮冰运动幅值的差异也逐渐缩小。

4 结 论

本文通过建立二维数值水池模拟了两种浮冰模型（带护栏/无护栏）在波浪中的运动，分析了有/无波浪冲洗现象对浮冰垂荡与纵摇运动的影响。研究发现：

（1）由于多浮冰与波浪的相互作用以及多浮冰的耦合相互干扰，浮冰对波浪具有一定的遮蔽和衰减作用，随着浮冰数目的增多，位于中间位置的浮冰运动相应变小，浮冰窄缝距离波浪入口越远，窄缝间的波浪运动也趋于平缓；

（2）无护栏浮冰由于受到波浪冲洗的作用，其运动幅值明显小于有护栏浮冰。同时，随着浮冰数目增加，中间浮冰受到的波浪冲洗现象减弱，该浮冰运动幅值的差异也逐渐缩小。

本文通过二维数值模型研究了浮冰有/无上浪现象对浮冰运动的影响，研究发现，上浪导致的冲洗现象对浮冰运动具有一定的抑制作用，随着浮冰数目的增多，波浪冲洗现象减弱，其对浮冰运动的抑制作用也减弱。为了考虑冲洗现象对浮冰运动的影响，可参照本文采用有/无护栏浮冰模型来模拟浮冰的运动。本文计算中采用的加护栏的浮冰模型对于研究浮冰在波浪下的运动具有一定的参考意义。此外，当流场和浮冰运动具有明显三维特征时，可参照本文建立的分析方法在三维物理场内开展相关研究。另外，对于大尺度浮冰还需进一步考虑其在流场动压力作用下的弹性效应与破碎。