船体结构冰载荷的时域反卷积识别算法及信号采样周期选取
2021-09-02田于逵崔洪宇季顺迎
孔 帅,田于逵,崔洪宇,季顺迎
(1.中国船舶科学研究中心,江苏无锡 214082;2.大连理工大学工业装备结构分析国家重点实验室,辽宁大连 116024)
0 引 言
冰区船舶作为运输和破冰利器,在极地科学考察、通航和资源开采中都必不可缺[1]。为保证冰区船舶结构的安全性,不仅需要有严格的建造标准,更需要设计人员了解船体冰载荷分布规律以优化设计结构[2-3]和分析冰激疲劳损伤特性[4]。冰载荷的实船测量是开展冰载荷研究和保障其冰区航行安全的重要手段[5-7]。在实船测量时,冰载荷通常是利用测得的结构响应(加速度、速度、位移和应变等信号)和载荷识别模型来识别的,其识别载荷过程对应动力学中的第二类反问题。因此,适宜的冰载荷识别模型是冰载荷精细化测量的核心[8-10]。
船舶在冰区航行时,其肋骨是海冰与船体碰撞过程中的主要承力构件,因而肋骨常作为冰激应变的监测构件[8,10-12]。Suominnen等[11]通过绞盘机装置对肋骨进行了加载,结果表明其加载力和肋骨剪切应变之间成正比。因此,船体结构冰载荷识别中常采用影响系数矩阵的形式将冰载荷与肋骨剪切应变关联起来,该算法核心为结构的局部应变仅为外载荷静力作用下产生的变形,不考虑结构的阻尼特性。冰载荷作为典型冲击载荷,其动载荷识别技术尚未有学者做有效考虑。时域反卷积算法是目前时域载荷识别法中较为常用的方法,其适用的识别载荷类型较为广泛,包括平稳载荷、非平稳载荷和冲击载荷[13-15]。然而,时域反卷积法的核函数矩阵在所求载荷数目较大时会导致矩阵规模较大,且其基于递推连锁计算格式的算法对初值的敏感性较高,初值选取不当会导致较大的累积误差。为控制载荷识别中出现的求解不稳定问题,可采用结合正则化算法[16]和相关正则化参数优选理论[17]的方法进行控制。
冰载荷识别中信号采样周期设定具有较强的经验性和主观性,如Ritch 等[18]在CCGS Terry Fox 号冰山撞击测试时选用的采样频率为500 Hz;Kotilainen 等[19]在PSRV S.A.Agulhas II 号于波罗的海测试时的采样频率设置为200 Hz;Kwon 等[20]在ARAON 号于阿蒙森海测试时选用的采样频率为50 Hz。而事实上,冰激应变信号采样周期是影响冰载荷监测系统识别精度、稳定性和预报及时性的关键因素。当采样周期过大时,其识别结果可能会严重偏离真实冰载荷,造成冰载荷监测系统的错误报警。而采样周期过小时,其识别载荷的精度未必会提升[21],且其识别效率也会大幅度降低,延误报警时机。针对动态载荷识别,不同采样周期准则的原理差异性较大。如唐秀近[21]建立的采样周期准则依据于信号的采样定理;文祥荣等[22]针对精细逐步积分方法建立了等步长采样周期选取准则;蔡元奇等[23-24]则从缩小解的空间和增加约束条件的方式建立了采样周期选取准则。
为确定船体结构冰载荷监测中信号采样周期,本文将结合Green核函数和Tikhonov正则化方法建立冰载荷识别模型,根据实测冰载荷数据、船体外板自振特性和采样原则进行讨论分析,并通过分析算例中的载荷识别精度对优选的采样周期的适用性作评估。
1 基于时域反卷积算法的船体冰载荷识别模型
基于时域反卷积法的冰载荷识别模型是一种典型的动载荷识别模型,可有效考虑结构阻尼等高频载荷特征[13-15]。为确定冰载荷的分布规律,对每个监测子区域上的冰载荷要通过多源冰载荷识别算法进行识别分析。根据线性时不变系统的叠加原理可知,对任意动态载荷引起的应变响应可用一系列单位冲击载荷的响应叠加而成。船体结构在多源载荷作用下的响应是各个监测子区域上载荷引起的响应的线性叠加,因此可将多源冰载荷识别问题表示为如下矩阵形式:
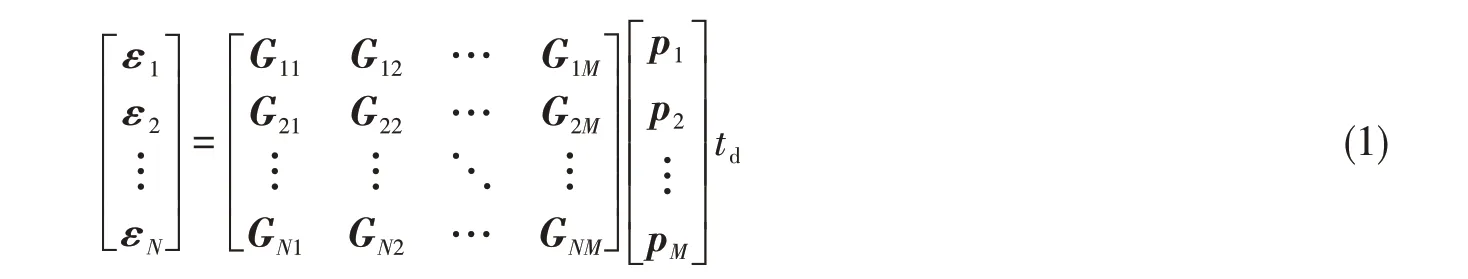
式中:M为需要监测子区域的数目;N为测点的数目;pi为每个监测子区域上的冰载荷时程;εi为测点上的应变时程;td为时域反卷积算法的离散时间间隔,该时间间隔可与信号采集时间间隔相一致;Gij为i监测子区域上冰载荷与j测点应变之间的Green核函数矩阵。
实际工程中的反问题稳定求解应满足三个条件,即解的存在性、解的唯一性和解的稳定性。而在载荷识别中,求解问题的不适定通常指的是解的不稳定性。在早期的动载荷识别中,学者通常采用直接求逆的办法,导致载荷识别结果往往与真值相差较大。为提升识别结果的稳定性,常用的技术手段是引入正则化方法。正则化方法是由苏联学者Tikhonov[16]提出,为处理病态的反问题提供了坚实的理论基础。基于变分理论的Tikhonov 方法也是目前载荷识别中应用最为广泛的正则化算法[16],可有效识别桁架结构[25]、壳体结构[26]及轴系[7]所受载荷。为提升求解的稳定性,采用Tikhonov正则化算法后的解可写作:
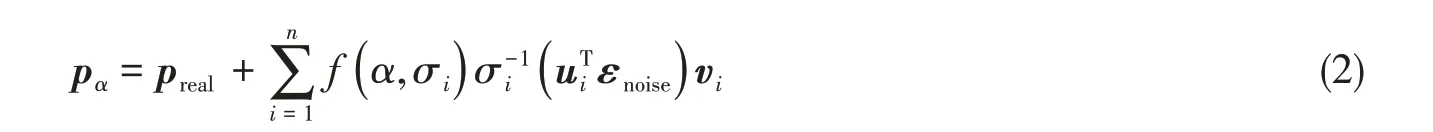
式中:pα为采用正则化算子后获得的解;preal为真实解;σi为矩阵G的奇异值;vi为核函数矩阵G的右奇异向量;ui为核函数矩阵G的左奇异向量;G由式(1)中Gi j组装形成;εnoise为测试应变信号的噪声部分;f(α,σi)为Tikhonov正则化算子,其定义如式(3)所示:

正则化算法载荷识别精度和稳定性与正则化参数α相关性很强,可采用广义交叉检验法(generalized cross validation,简称GCV)进行正则化参数优选[17]。GCV 准则基本思想是在测量值中的任意一数据点被移除时,所选择的正则参数能预测到移除数据所导致的变化。由于移除数据没有被包含在内,可作为独立观察项。将直接识别得到的解与移除数据得到的解进行比较并得到预测误差,然后对其它测量项重复这个过程。GCV 将整体预测误差的平方和最小作为正则化参数α优选的标准。GCV 可以等效为求解GCV 函数最小值问题,图1 为采用GCV 准则确定最优正则化参数α的示意图。GCV 函数V(α)可由式(4)求得:
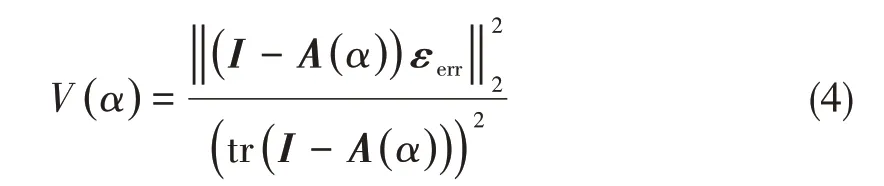
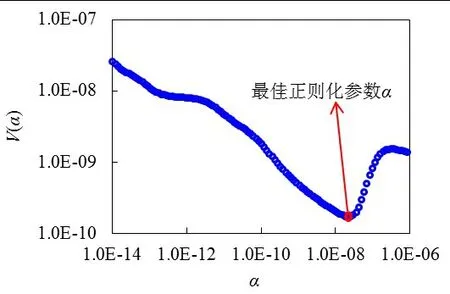
图1 基于广义交叉验证准则的正则化参数优选Fig.1 Optimization of regularization parameters based on the generalized cross validation criteria
式中:tr( · )为矩阵的迹,即矩阵主对角上各个元素的总和;I为单位矩阵;A(α)为中间变量,A(α)=G(GTG+αI)-1GT。
2 信号采样周期的选取分析
实际分析表明,信号采样周期的设定对载荷识别结果的影响很大,采样周期的随意设定可能造成识别载荷信号的严重失真,且其计算量也难以控制。因此,冰载荷识别过程中采样周期的设定应具有良好的普适性[21,24],但学者对冰载荷识别问题中的采样周期选取标准尚未进行讨论。
为完整保留原始信号信息,采样定理规定采样频率必须大于连续信号最高频率的二倍。因系统的振动特性也应是识别动态载荷的关键,唐秀近[21]在采样定理的基础上又增加考虑了结构的自振特性,即:

式中,ff为冰载荷最高频率;fn为根据实际需要确定的结构最高模态频率。
为进一步保证载荷识别中求解的精度和稳定性,蔡元奇等[24]从识别问题的不适定性角度出发建立了新的采样周期选取准则:

式中:Δt为采样周期;δ为单位为%的常量,用于控制求解的精度,本文将其设定为1%。
综合式(5)和式(6)优点,笔者建议的采样周期为

式中,fT为兼顾了结构自振特性和输入载荷频率的变量。
综上可知,计算采样周期时,冰载荷频率和结构自振特性的范围是十分重要的。
首先,考虑船体结构冰载荷频率。实际上,海冰通常存在多种类型,且在洋流热力动力作用下重叠冰、冰脊等复杂冰型出现几率较高,影响海冰的均匀性。另外,破冰船虽然具有一定的破冰能力,但在极区航行时通常选择冰间水道,尽量避免与海冰碰撞。这些因素导致冰载荷周期在参数分析和分布拟合分析时具有较大难度。因此,目前仅有极少数学者从事船体冰载荷周期研究[5]。分析南北极现场航行影像资料可知,破冰船与海冰之间的作用是随机的,并不是确定性事件。泊松分布适用于描述单位时间内某随机事件发生的次数。泊松分布也常被用于船舶结构冰载荷的空间分布和时间分布分析,如Kujala 和Arughadhoss[6]对MT Uikku 号的冰池及现场试验结果分析后可知特定面积内海冰碰撞单元数目满足泊松分布;Suyuthi 等[5]对KV Svabard 号于2007 年在巴伦支海航行时冰载荷峰值进行了统计,发现其也满足泊松分布。泊松分布概率密度函数为

式中:P(n)为概率密度函数;n为单位时间内发生船冰碰撞事件的次数;γ=λsh,表示统计时间内随机事件出现的次数;h为事件统计时间;λs为单位时间内随机事件发生的平均次数。
由统计学知识可知,事件的发生若满足泊松分布,则其事件间的时间间隔可采用指数分布的形式进行描述。针对冰载荷峰值时间间隔指数分布的概率密度函数f(t)可写作[5]:

式中:λ= 0.236 为指数函数参数;t为对应冰载荷峰值的时间间隔,可由峰值自动提取程序确定[27]。
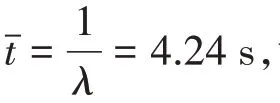
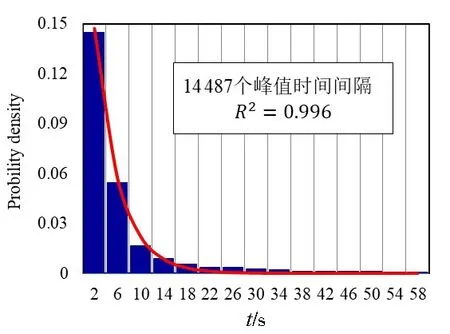
图2 峰值时间间隔的对数概率分布[28]Fig.2 Exponential probability distribution of time intervals between the subsequent extremes[28]

式中,F(t)为对应式(8)定义概率密度函数的超越概率。
其次,考虑冰区船外板结构的自振特性。基于整合了不同船级社规范及指导手册的外板结构一阶固有频率预估方法可知[29],外板结构的自振频率远高于冰载荷的最高频率。因而,由式(7)和式(8)定义的采样周期选取准则决定因素为外板结构的自振频率。
因冰区船外板结构尺寸比例、加筋方式和板厚等变量的不同,船体外板结构固有频率具有差异性,如中国极地科考破冰船“雪龙2号”破冰船、中远冰区运输船“天恩号”和Kõrgesaar 等[30]研究中采用的外板结构,其固有频率分布在23 Hz 至26 Hz 之间。另外,通过ANSYS 模态分析可知Kõrgesaar 等[30]采用的外板结构第五阶固有频率为25.08 Hz。综合考虑外板结构自振特性的离散范围和时间步处理的便捷性,由式(7)和式(8)计算的采样频率可选取到250 Hz,后续计算均采用此值。
3 基于冰载荷识别算例分析的采样周期准则评估
在基于Green核函数和正则化方法建立冰载荷识别模型的基础上,可通过外板结构载荷识别算例对采样周期选取准则的适用性进行评估。
3.1 船体外板结构模型
各国的冰区船舶外板结构因依据不同的冰级规范建造而导致差别较大。本文采用的结构模型主要参考“雪龙2 号”外板结构和其他学者[30]采用的外板结构,建立的外板结构由肋骨、强肋骨、纵桁和外板组成,其具体尺寸信息标记于图3。在冰载荷识别过程中,船体结构假设处于线弹性阶段。结构阻尼选择为比例阻尼。弹性模量为206 GPa,泊松比为0.3,结构钢材密度为7 850 kg/m3。边界条件参考ABS 冰级船规范标准,在模型的上下界面内边的边界设置为在x方向自由,左右界面内边的边界设置为关于yoz面对称[30]。模型中间部分采用较为精细的网格,网格尺寸为50 mm×50 mm,为提升计算效率,其余部分采用尺寸为150 mm×150 mm的网格。
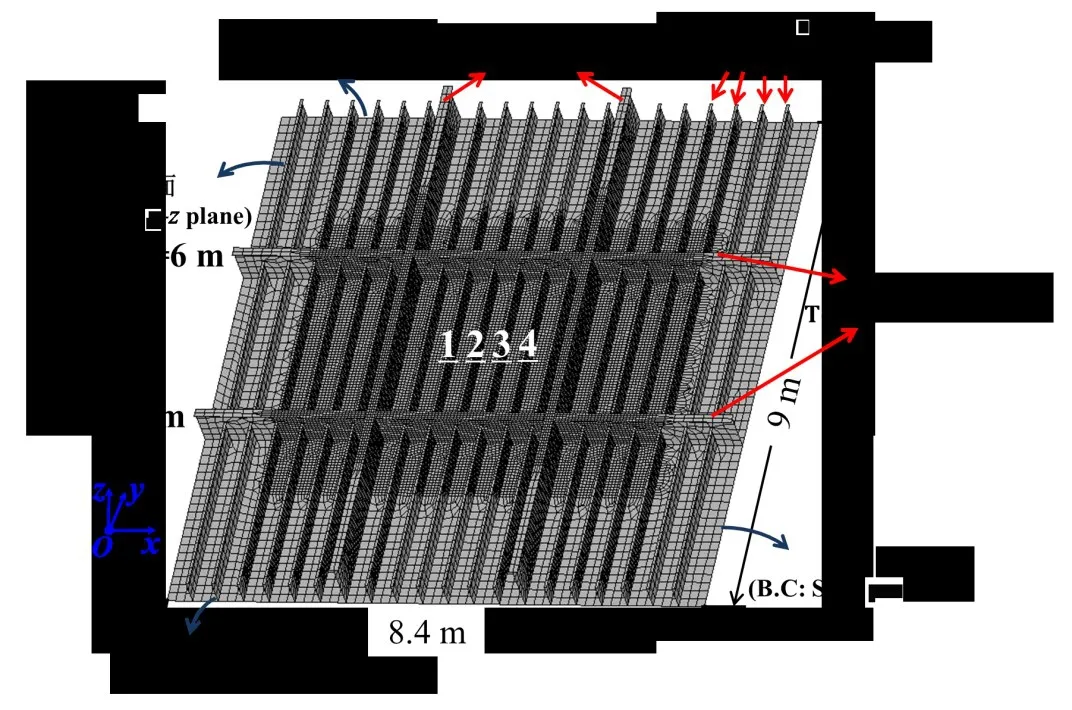
图3 典型冰区船舶外板结构有限元模型Fig.3 FE model of typical shell structure of ice-going vessel
3.2 载荷识别工况构造
船体冰载荷监测系统的建立需预先根据监测需求设定监测子区域。通常假设如图4(a)中监测子区域中a、b两点之间的冰载荷是一个均匀分布的载荷,即p1。本文采用的监测子区域分布如图4(b)所示,在Frame 1至Frame 4上划分四个子区域,其子区域的面积为0.4 m×0.4 m。基于肋骨冰激应变监测的冰载荷识别是目前主流技术手段[8,10-11,18]。分析外板结构试验中冲击载荷-应变信号可知,当应变测试位置靠近肋骨边缘且测试方向平行于外板时相关性最佳[31],故选择图4(b)右侧黑圆点为冰激应变监测点。
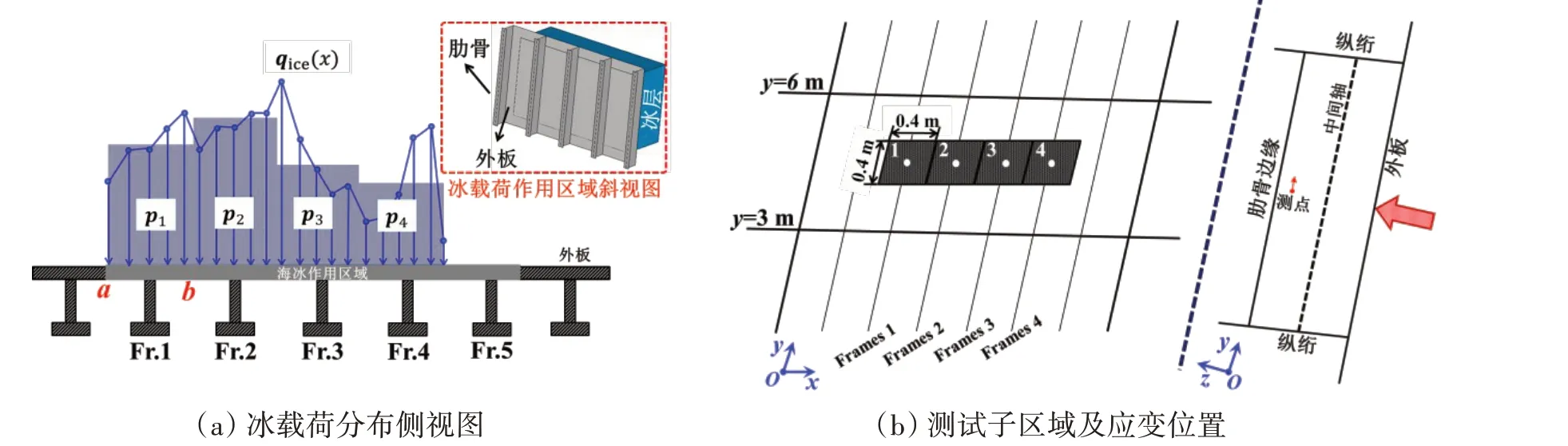
图4 肋骨上子区域和应变传感器的布置Fig.4 Layout of sub-panels and strain sensors on the frames
为分析采样周期对冰载荷识别精度的影响,需要根据冰载荷特征构造施加载荷时程。破冰船破冰过程中,海冰在船体的持续作用下发生碰撞、翻转和滑移等过程,其中海冰与船体刚发生接触时至海冰断裂过程中,冰载荷一直稳步上升直至海冰发生断裂,这时冰力达到最大值。之后,冰载荷会在海冰翻转过程中逐步降低。海冰最终将会顺着船体水线处滑移开,此时冰载荷对应最小值。图5(a)所示为PSRV S.A.Agulhas II 号于2012 年在波罗的海实测的一个冰载荷周期的时程曲线[19],从图中可看出冰载荷呈现出三角波的形式。典型破冰船外板冰载荷承载能力研究工作中也采用三角波的形式模拟冰载荷时程[32]。因此,冰载荷时程数值分析可采用式(12)定义的三角波,图5(b)所示为对应的三角波形式的施加载荷时程。
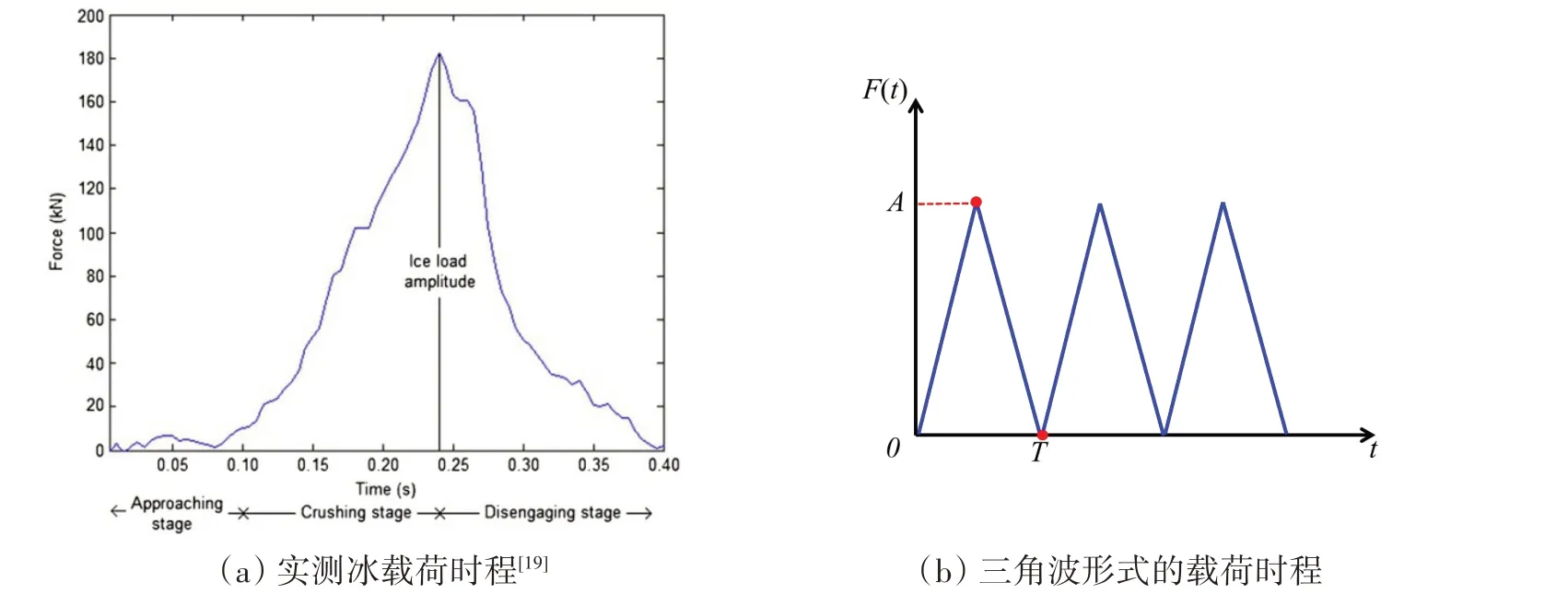
图5 PSRV S.A.Agulhas II号测量的冰载荷和数值模拟中施加的载荷时程Fig.5 Ice loads measured on PSRV S.A.Agulhas II and history curve of applied loads in numerical study
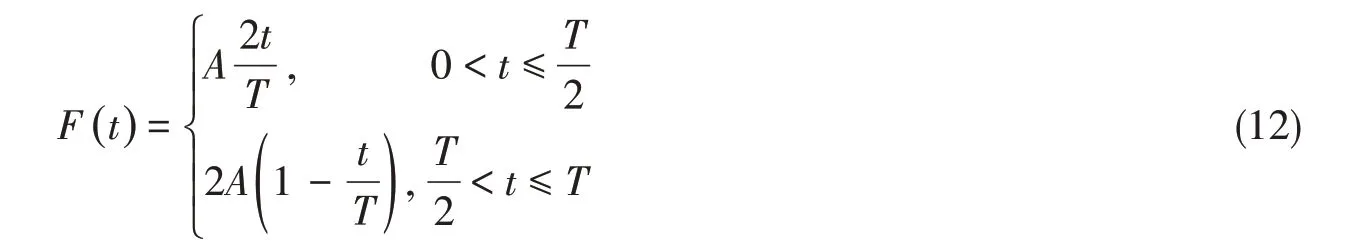
式中,F(t)为施加载荷时程,A为三角波的幅值,T为三角波周期。
实船冰载荷测量中,其冰激响应信号始终存在噪声的干扰,噪声信号会对识别数值产生较大的干扰。为分析噪声信号对冰载荷识别模型干扰程度,采用加性噪声的形式进行添加,其实际结构测量的应变信号可写作[13]:

式中:ε为结构的冰激应变信号;εerr为含有噪声信号的应变信号;lnoise是一个百分数,表示噪声水平;std(ε)为ε标准差;rand( -1,1 )为( -1,1 )之间的随机数。
3.3 采样周期选取准则的评估分析
为分析由式(7)和式(8)定义的采样周期的适用性,将三角波频率分别设置为2.0 Hz 和4.0 Hz,其幅值均设置为1 000 kPa。同时向图4(b)中设定的四个监测子区域施加载荷时程,并构建不同噪声水平的信号,其中噪声水平从0%增至10%,增加步长为1%。图6(a)和图6(b)分别为在不同噪声水平信号干扰下采用两种采样周期识别载荷的相对误差,可知载荷识别误差受信号噪声水平影响较大。两种工况中识别误差的平均值分别为4.61%和4.85%,可知由式(7)和式(8)定义的采样周期识别普适性较好。另外,施加载荷频率的提升对载荷识别误差也有影响,而船体结构冰载荷的频率具有一定的随机性,实际载荷测试中应采用更小的信号采样周期,建议其测试频率设置在300 Hz至500 Hz之间。
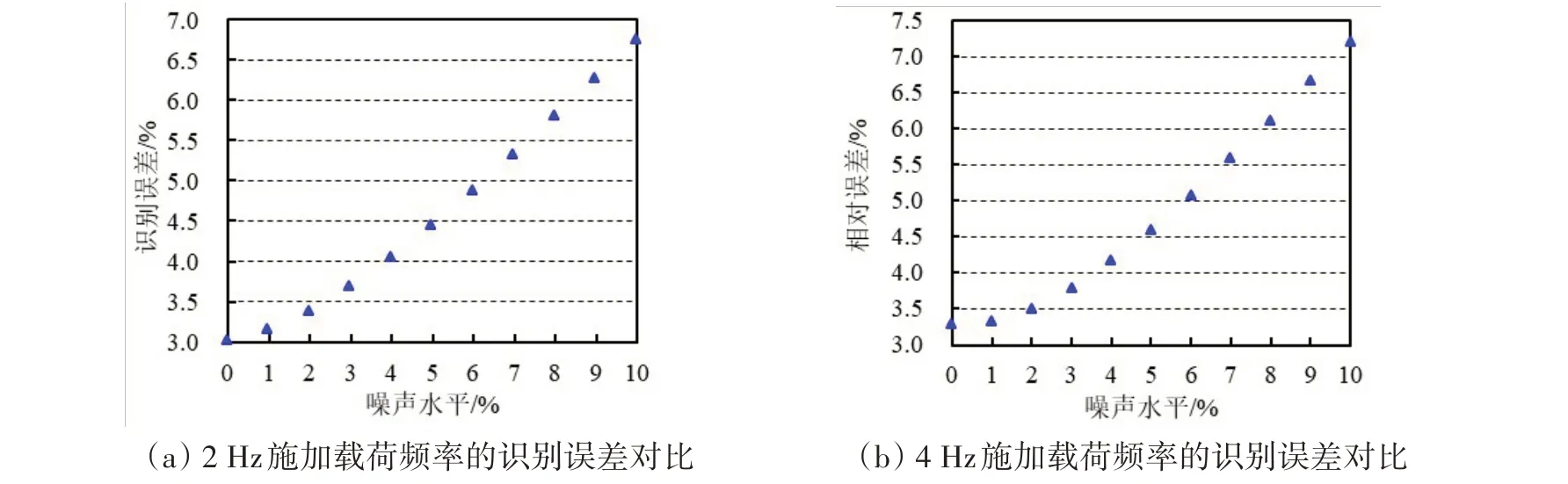
图6 两种施加载荷频率模拟工况中不同采样周期对识别精度的影响Fig.6 Influence of different sampling time on the identification error in the two simulated cases with different frequencies of applied loads
为评估选取的采样周期在施加载荷随机性更强工况中的适用性,识别图7中粗实线所示的各肋骨上施加的载荷。实船冰载荷监测系统是准实时系统,其冰载荷识别效率直接影响其预警的及时性。冰载荷识别程序由MATLAB 2014a运行,CPU处理器为Intel Core i5-3470。若载荷分析频率为200 Hz,则运行时间为13.25 s;若载荷分析频率为40 Hz,则运行时间为1.32 s。图7 中的载荷分析频率为40 Hz,可以看出,对于常见的三角波形式的冰载荷时程而言,其识别载荷可较好地对应上施加载荷时程(对应整体识别误差为7.2%),并能较为准确地识别出载荷峰值,故建议实船冰载荷监测系统中的分析频率不必设置过高。另外,工业界常用的影响系数矩阵法会因周边肋骨或外板上的冰载荷而干扰其对应位置上识别数值[33],而本算例中每个肋骨识别的载荷均未受到周边结构上施加载荷的影响,该方法在实际应用中可有效提升冰载荷分布特征提取。
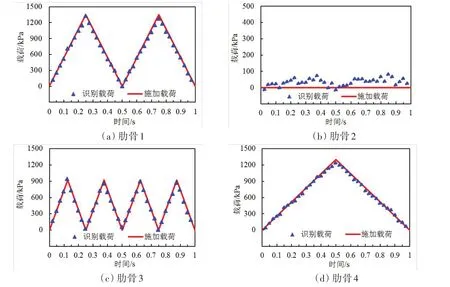
图7 数值算例中识别载荷与施加载荷对比Fig.7 Comparison between the identified loads and applied loads in the numerical cases
4 结 论
本文结合Green核函数、Tikhonov正则化算子和广义交叉检验正则化参数优选法等方法建立了船体结构冰载荷识别模型,并对其采样周期选取进行了研究,可得出以下结论:
(1)本文提出的结构冰载荷采样周期选取准则(式(7)和式(8))既考虑到冰载荷频率,又考虑了船体结构的固有频率特征,其中δ的选取又保证了波形的重现度;该准则集合了式(5)和式(6)的优点,具有较好的工程适用性。
(2)随着信号噪声水平增加,载荷识别误差也随之增加。随着采样频率的增加,结构冰激响应信号的失真程度会减小,同时也可能会引入不必要的噪声。随着采样频率的增加,时域反卷积算法的求解时间会延长,其连锁递推迭代算法也会对噪声起放大作用。
(3)后续将采用更为高级的低通滤波器和随机噪声数字滤波技术以进一步屏蔽噪声信号;利用形函数模型以减小反求矩阵的奇异性,采用高性能算法以提升冰载荷识别模型的实时性。
