基于环向裂纹法的气垫平台破冰载荷数值模拟

金江杰，周 利，丁仕风

（江苏科技大学船舶与海洋工程学院，江苏镇江 212000）

0 前 言

北极地区的重要性日益凸显，其不仅拥有丰富的矿产资源，还可以给货物运输提供便利航道。现已探明的北极自然资源大部分位于浅水的大陆架附近，由于水深的限制，常规的破冰船无法进入这些水域进行破冰，因此有必要研究一种适用于浅水水域的破冰工具，以增加我国在北极区域的通行能力[1]。气垫船凭借其独特的构造，可以出色完成破冰、运输、救援等任务。

近年来，国内外部分学者对气垫船破冰进行了研究。Muller[2]通过理论分析建立了气垫船低速破冰时冰层的受力模型，并提出了气垫船在高速与低速下的破冰机理。Hinchey和Colbourne[3]进行了气垫船低速破冰的模型试验，分析了气垫船低速破冰时的阻力；Hinchey[4]进行了冰层下气腔扩散的模型实验，基于实验结果提出重力流模型更适合描述冰层下空气腔的传播，从而否定了水下爆炸的传播模型。本文介绍了基于环向裂纹法[5-6]对低速下气垫船的破冰载荷进行的模拟，以及结合数值计算模型，对冰力时历曲线的分析。

1 理论模型

1.1 破冰机理

气垫平台破冰模式可以分为两种，即低速模式和高速模式，又可称为静态破冰和动态破冰。在低速模式下，气垫平台在全垫升状态从水中低速接近冰层时，气垫船的高压气体喷向水面，会将气垫船附近的水排开，形成凹陷的圆面，并且会辐射至附近冰面的下方，在冰层下方形成气腔，形成冰层悬臂梁效应。随着气垫平台不断接近冰层，冰层下方形成的气腔长度不断增加。当气垫平台首部围裙开始接触冰面时，气腔长度达到最大。接触面积随着船的前进而增大，当船对冰层合力达到冰层所能承受的最大力时，冰层将发生破坏。因此，气垫平台低速模式下破冰的基本原理就是通过高压气体取代冰层下方的水，形成悬臂梁效应，使冰层更加容易破裂。

1.2 环向裂纹法

在平整冰与船体相互作用的过程中，冰块会承受竖直方向的拉压作用和水平方向的拉伸作用。在这两种应力的作用下，冰块会发生平行于接触面方向的环向裂纹或者垂直于接触面方向的径向裂纹。基于这种物理现象所进行的数值模拟被称为环向裂纹法。

假定冰块在竖直方向上发生断裂，其接触表面是平的，接触面积可由接触长度和接触深度来确定。平整冰破碎后产生的浮冰的几何形状可假设为扇形，破碎扇形冰角度为θ，破冰半径可根据文献[7]给出的表达式来计算：

式中，Ei为海冰的弹性模量，hi为冰层厚度，ν为泊松比，ρw为水密度，g为重力加速度。

1.3 船-冰作用数学模型

随着气垫平台的前进，气垫围裙与海冰接触面积逐渐增大，对冰产生的挤压力也逐渐增大。在弯曲破坏发生前，发生在接触面的挤压力垂直于接触面向下，其挤压力计算公式为

式中，σc为海冰挤压强度，Ac为接触面积。

气垫平台的高压气体把冰下的水排开，形成一个气腔。此时，冰还受到自身重力G以及气体对冰向上的支持力Fc，当冰发生破碎时，形成的开角为θ的楔形冰块，因此，所受重力计算公式为

式中，θ为扇形角度。

当高压气体作用在水面时，水面会有一个向下的凹陷，凹陷深度d与气垫船的气垫压力有关。

式中，p为气垫压力，ρw为水的密度。

另外，冰层浮在水上，水面下的厚度为水面上的9 倍。因此当凹陷深度小于0.9 倍的冰厚，即d＜0.9hi时，冰层下方将无法形成气腔。因此，只有在水面凹陷深度d＞0.9hi时，冰层下方才会形成气腔，有利于气垫平台破冰。在Hinchey 的实验中，观测到空气腔在冰层下方向的外辐射呈半圆形，假设冰破碎半径就等于半圆的半径，在不考虑空气泄流的情况下，扩散半径与气腔高度的关系为

式中，h'为气腔高度，κ为实验确定的常数，取κ= 0.35。

根据Hinchey的实验结果得到冰下空气腔各处的压力符合流体静力学，即空气腔内压强为

式中，r为气垫半径。

因此，在气腔扩散半径等于扇形冰破碎半径时，高压气体对冰向上的支持力Fc在数值上可表示为

式中，A'为破碎扇形海冰的面积，R为破碎冰半径。

1.4 海冰失效判断

海冰的失效模式有挤压破碎模式和弯曲失效模式两种。在船冰作用时，海冰失效情况复杂，可能只发生单一失效，也可能两种失效模式混合发生。海冰的失效模式受多种因素的影响，主要有结构物倾斜角度、冰厚、结构物宽度，以及冰-结构物相对速度等。本文以气垫平台为研究对象，在气垫平台向前运动过程中，数值模拟中船体节点与海冰的相对速度，气垫围裙与海冰接触面的宽度都是变量。因此，文中冰的失效模式只考虑结构物（即气垫围裙）的倾斜角度。

在气垫平台运动时，与冰接触部分的气垫围裙和冰接触相互作用过程中，根据公式（5）和式（7），

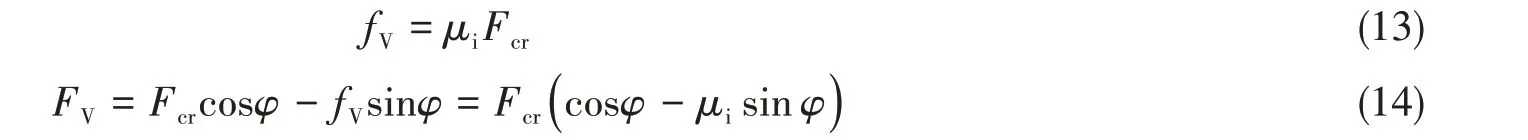
由上式可知，结构物倾斜角度的极限值与摩擦系数有关。当破冰结构的坡度角大于极限角时，冰发生破碎失效；当破冰结构坡度角小于极限角时，冰发生弯曲失效。当北极海冰与船体结构的摩擦系数0.05≤μi≤0.15[7]时，根据极限角与摩擦系数关系图可知极限角82°≤φ≤87°。因此，在坡度大于80°时，海冰不再发生弯曲失效模式，而是发生挤压破碎模式[8]。气垫平台通过气垫围裙与冰接触，文中气垫围裙的坡度一律取45°。因此，文中的海冰皆发生弯曲失效模式。

平整冰在破冰结构的作用下若发生弯曲失效，将形成一个开角为θ的楔形冰，楔形冰顶端受到的承载能力的估算式[9]为

式中，Cf为经验参数，σf为海冰的弯曲强度。

1.5 船舶运动方程

一般运动方程设（X,Y,Z）为右手坐标系，Z垂直向上，X向前运动，原点为船体重心。六个线性耦合的运动微分方程可以写成如下形式：

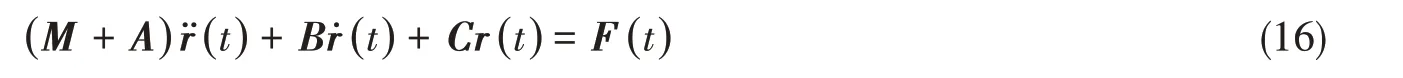
假设船舶横向对称，那么

式中，M为气垫平台的质量，I66为Z方向上的转动惯量。且在这三维体系中，阻尼与恢复力假定为0。

1.6 冰力计算方程

在气垫平台运动过程中，三维冰力的计算公式[10]为

1.7 推力计算方程

因为本次模拟气垫平台无自航能力，需要一艘船舶给气垫平台提供动力。假设推力在传递过程中没有损耗，那么气垫平台受到的推力即为母船的推力。净推力计算公式为

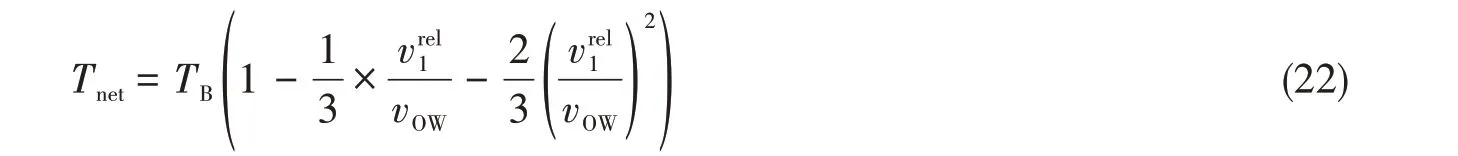
式中：TB为系柱拉力，一般在数值上取主机功率的1.5%[8]；vOW为敞水速度；是船与冰之间的相对速度前进方向的分量。因此，由螺旋桨和舵产生的力和力矩可以简单地写成

1.8 水动力计算方程

在计算水动力时，常用以下经验公式来计算：

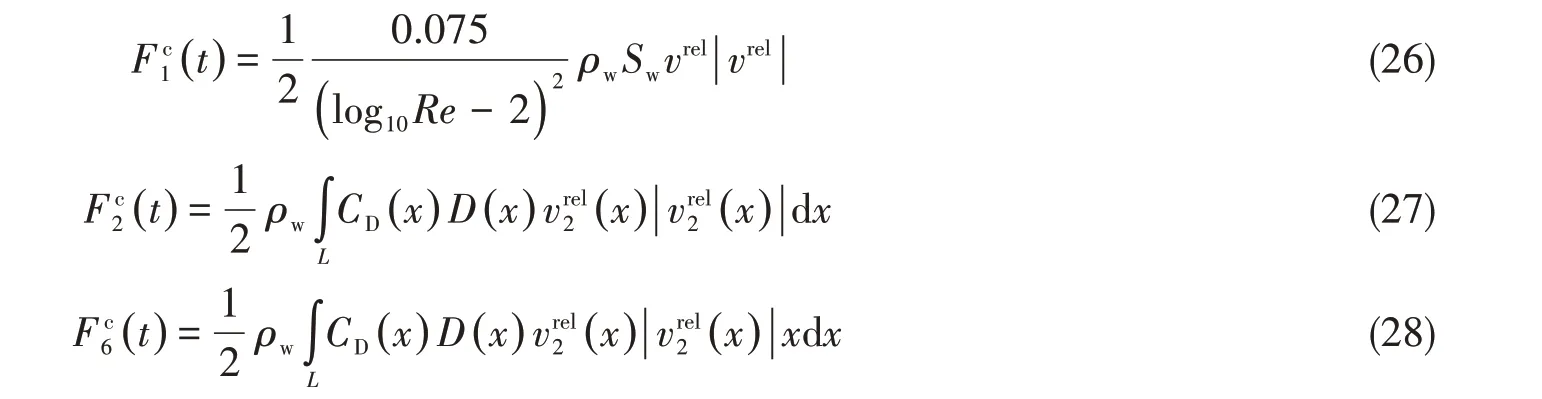
式中，积分域L为气垫平台长度，Re为雷诺数，Sw为气垫平台湿面积，CD为阻力系数，D为吃水。

在实际计算时，Tnet的计算中已经考虑了气垫平台运动方向的水动力，因此不考虑F1c(t)。

1.9 激发力方程

最后，激发力可以简单表示为冰力、螺旋桨力、水动力的合力：

2 数值模拟

2.1 数值模拟参数

本文数值模拟对象是直径为50 m 无自航能力的气垫平台，气垫船示意图见图1，船-冰模拟初始位置图见图2，船型参数见表1，海冰参数见表2。

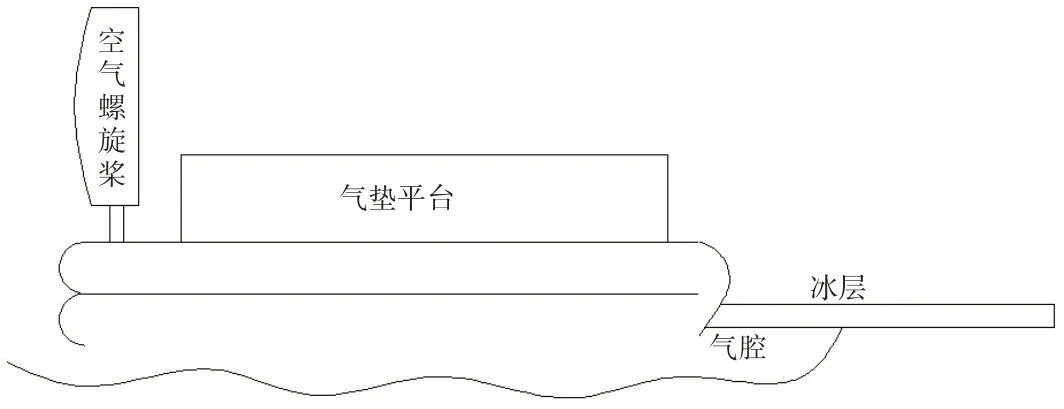
图1 气垫船示意图Fig.1 Diagram of hovercraft

图2 船-冰模拟初始位置图Fig.2 Ship-ice simulation initial position

表1 船型参数表Tab.1 Main parameters of ship

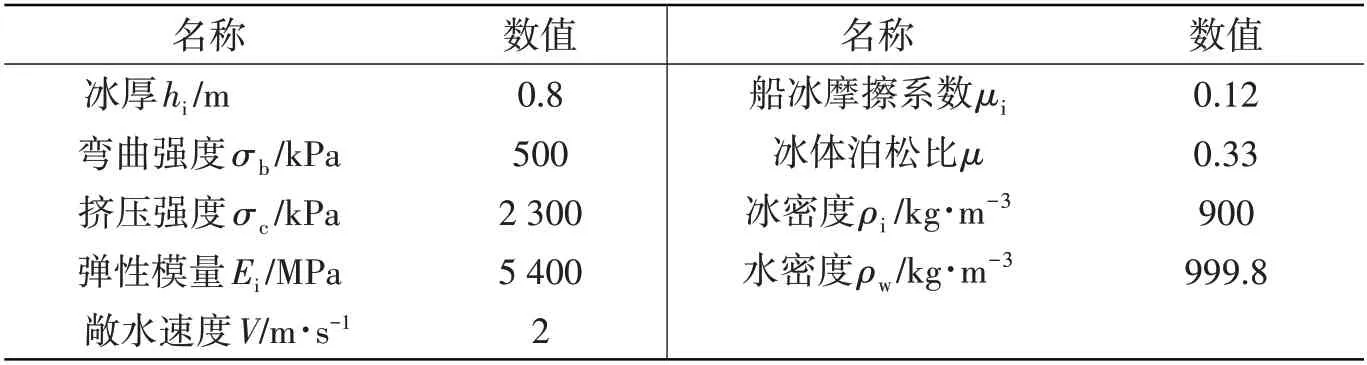
表2 海冰参数表Tab.2 Sea ice parameters

2.2 数值模拟结果

在冰下气腔扩散半径与冰破碎半径相同的情况下，以初速为0 m/s，冰厚为0.8 m，系柱推力为8×105N进行数值模拟。破冰速度维持一个动态平衡，平均速度为1.61 m/s，如图3所示；横向冰力时历曲线中冰载荷时历曲线具有一定的随机性，变化幅度较大，平均值为235.13 kN，如图4所示；纵向冰力时历曲线基本维持动态平衡，平均值为2.0 kN，如图5 所示；艏摇冰力矩平均值为21.19 kN·m，如图6 所示。

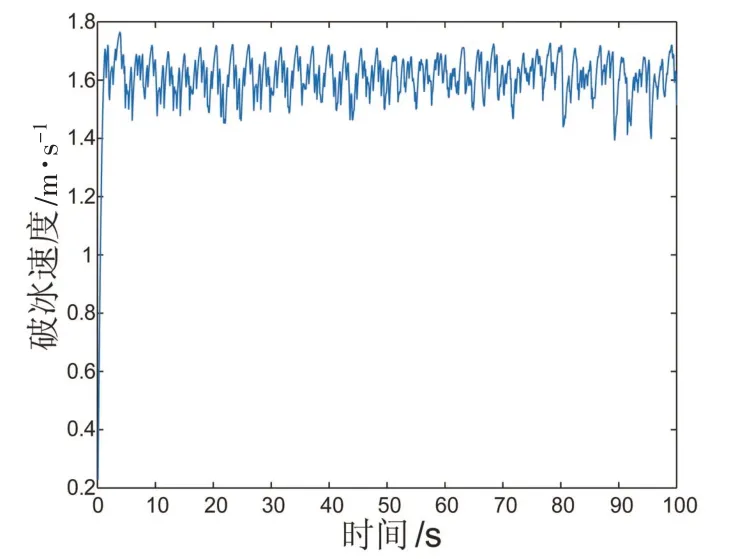
图3 破冰速度（有气腔）Fig.3 Ice breaking speed(with air chamber)

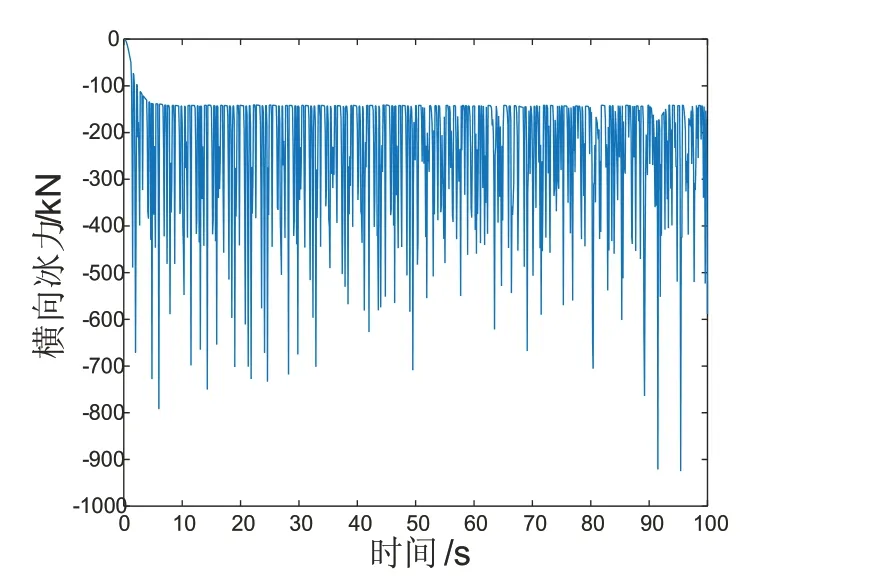
图4 横向冰力时历曲线图（有气腔）Fig.4 Ice force in surge direction(with air chamber)

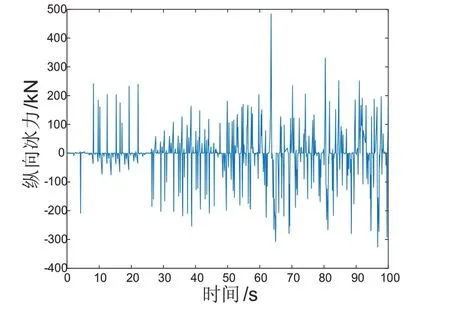
图5 纵向冰力时历曲线图（有气腔）Fig.5 Ice force in sway direction(with air chamber)

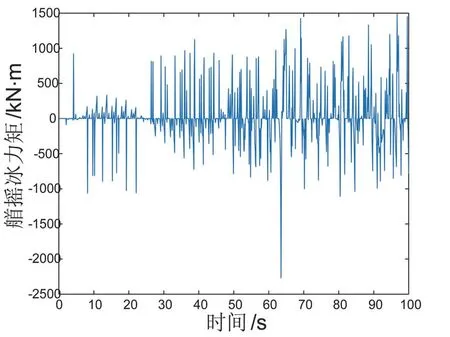
图6 艏摇冰力矩时历曲线图（有气腔）Fig.6 Ice moment in yaw direction(with air chamber)

当气垫平台气垫压力不足以在冰下形成空气腔时，即气垫船下方水面凹陷深度小于0.9 倍冰厚时，破冰速度较有气腔时，波动更大，更不稳定，平均速度为1.48 m/s，如图7 所示；横向冰力时历曲线平均值为300.44 kN，如图8所示；纵向冰力时历曲线平均值为10.13 kN，较有气腔时更大，如图9所示；艏摇冰力矩平均值为105.62 kN·m，如图10所示。横向、纵向平均冰力以及艏摇平均冰力距较有气腔时更大，且时历曲线波动明显，更不稳定。说明气腔可以减少气垫平台在破冰过程中Y方向上的位移，有利于提高气垫平台破冰的稳定性。

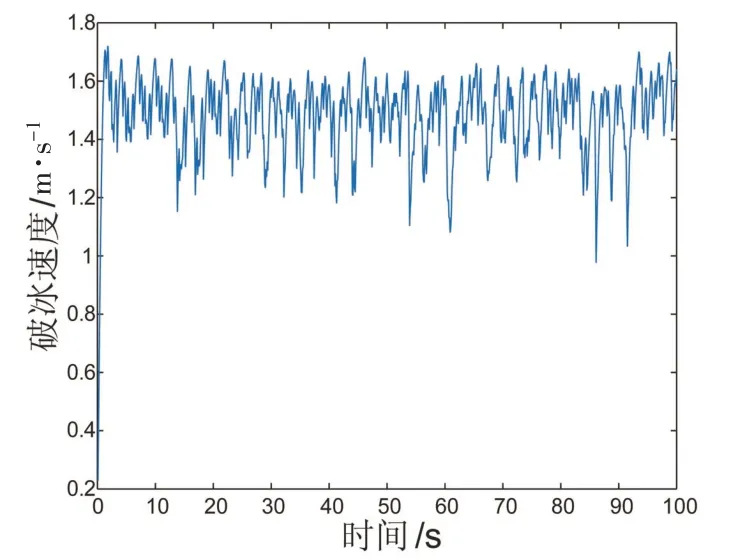
图7 破冰速度（无气腔）Fig.7 Ice breaking speed(without air chamber)

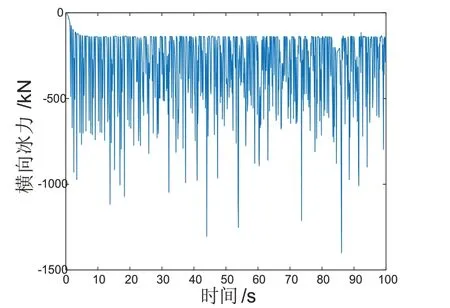
图8 横向冰力时历曲线图（无气腔）Fig.8 Ice force in surge direction(without air chamber)

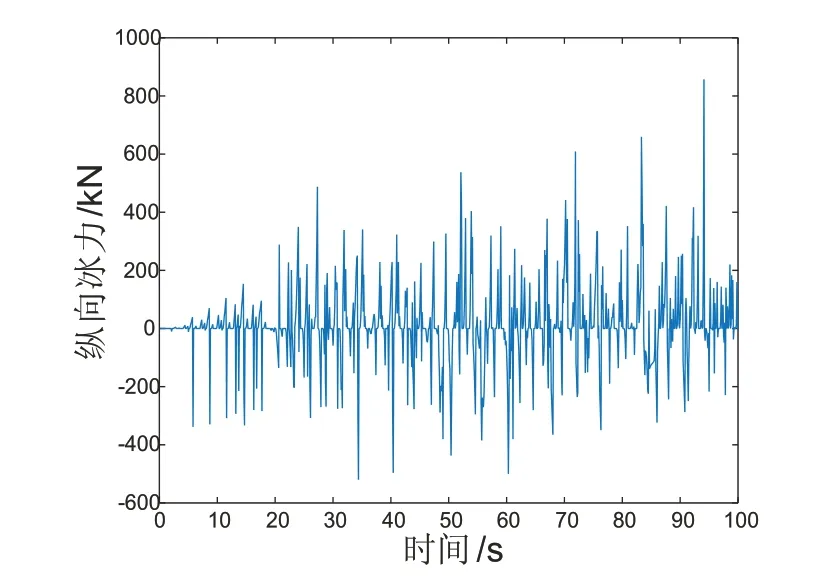
图9 纵向冰力时历曲线图（无气腔）Fig.9 Ice force in sway direction(without air chamber)

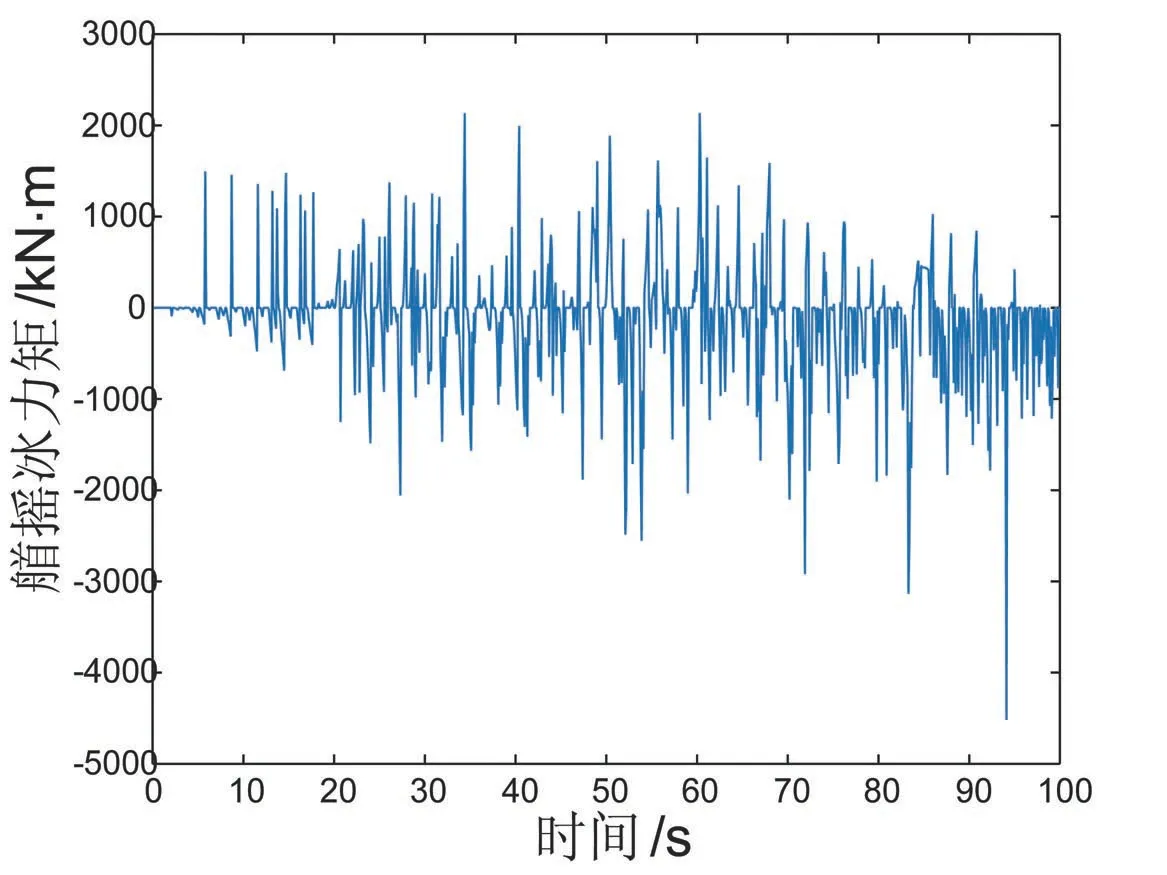
图10 艏摇冰力矩时历曲线图（无气腔）Fig.10 Ice moment in yaw direction(without air chamber)

对两种情况下的冰力进行对比，气垫平台的气垫压力只有在将水排开的深度大于冰厚时，才能在冰下形成气腔，从而帮助气垫船破冰。冰下有气腔与无气腔时的横向平均冰力与艏摇平均冰力矩如表3所示。

表3 模拟冰力以及冰力矩均值对比表Tab.3 Mean value of ice force and ice moment

根据文献[4]，假设气垫平台下方气垫压力均匀分布，且气垫压力p的变化会使气腔高度以及气腔扩散半径发生变化，从而使冰力发生变化。在不同气垫压力下冰力时历曲线如图11所示。

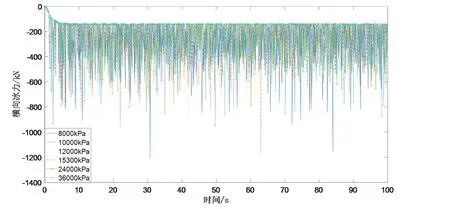
图11 不同气垫压力工况下冰力时历曲线图Fig.11 Ice force under different cushion pressures

2.3 结果分析

此次数值模拟中，不同气垫压力下的平均冰力与最大冰力见表4；平均冰力随气垫压力变化趋势见图12；最大冰力随气垫压力变化趋势见图13。分析数值模拟结果可以得知气垫平台在15.3 kPa 的压力下，能以1.61 m/s的速度破0.8 m 厚的冰。气垫压力在15.3 kPa时，冰下气腔扩散半径等于海冰碎裂半径，此时平均冰力达到最小，为235.13 kN。在此情况下，最有利于气垫平台进行破冰。在气垫平台的气垫压力不足以形成气腔时，即在相同条件下普通破冰船冰力为300.44 kN时，横摇力矩更大，不利于破冰，且破冰速度比有气腔时更慢。

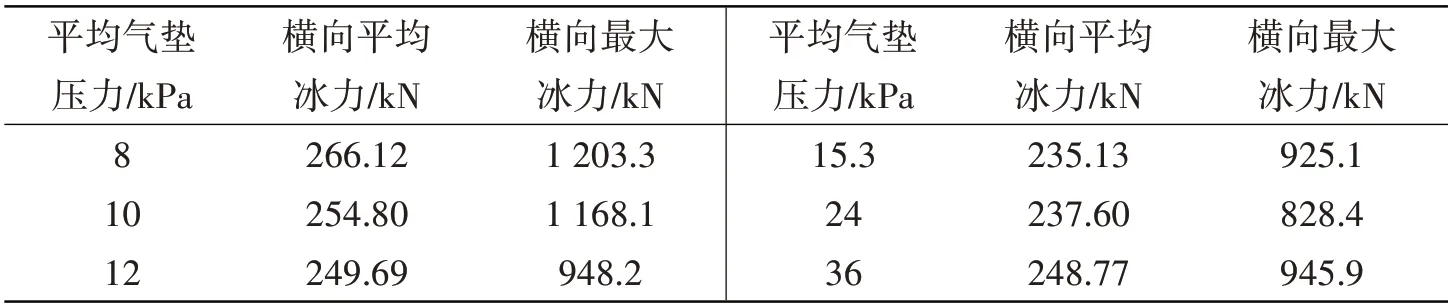
表4 不同气垫压力工况下平均冰力Tab.4 Mean value of ice force under different cushion pressures

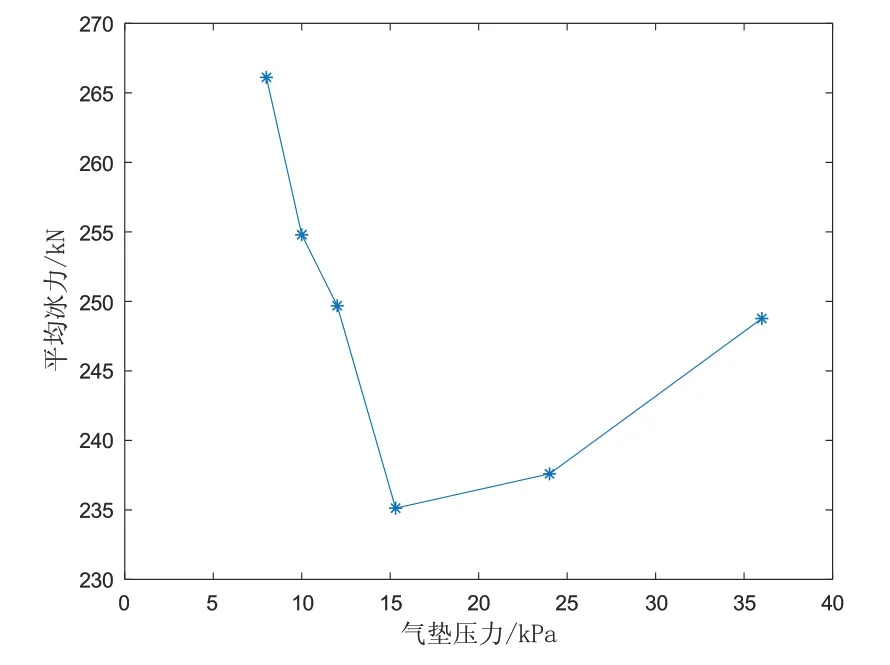
图12 平均冰力随气垫压力变化Fig.12 Mean value of ice force versus cushion pressure

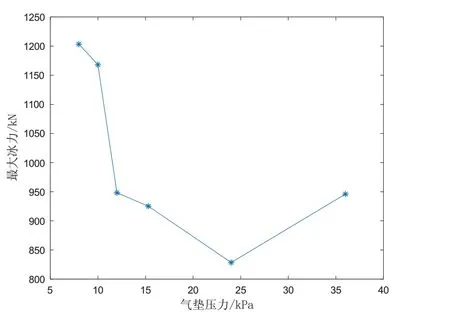
图13 最大冰力随气垫压力变化Fig.13 Maximum ice force versus cushion pressure

同时，气垫压力的变化会影响冰力的大小，在气腔扩散半径小于破冰半径时，即7 kPa＜p≤15.3 kPa，冰力会随气垫压力的增大而减小。当气腔扩散半径大于破冰半径时，即p＞15.3 kPa，冰力会随气垫压力的增大而增大。

3 结 语

本文基于环向裂纹法对气垫平台低速下破冰过程进行了数值模拟。在理想化假设下，对气垫平台低速破冰过程中冰体受力进行了分析，对气垫平台的破冰机理以及海冰失效模式进行了研究，获得了气垫平台低速下在给定冰厚下的最佳气垫压力数值，以及气垫平台在低速下的冰力随着气垫压力改变的变化趋势，即气垫平台的破冰能力在一定条件下与气垫压力有关，这是因为气垫压力的改变会使气腔扩散半径以及气腔高度也随之发生改变，这会使冰块碎裂的最小冰力发生变化，从而影响气垫平台的破冰能力。

本文的研究工作对冰区气垫破冰平台设计和研发具有一定的指导意义。然而，具体的冰载荷数值预报结果还需与具体实验数据进行对比，需要开展深入的研究。