卫星姿控飞轮电机锁相环稳速非线性协同控制

魏鸿超，王志强

(北京航空航天大学 仪器科学与光电工程学院，北京 100191)

0 引 言

反作用飞轮通过精确地跟踪姿控系统力矩信号给定指令，达到调整卫星姿态或者补偿系统干扰力矩的目的[1-2]。当给定零转矩指令时，要求飞轮电机的转速具有较高的稳速精度，而锁相环稳速控制技术是高精度磁悬浮反作用飞轮工作在速率保持模式下的最佳控制方案。

锁相环控制技术主要目的是改善电机动态性能和提高系统抗干扰能力。在最初阶段，锁相环控制系统采用的是通过模拟电路实现的单一锁相控制，控制方案简单。采用MC4044鉴频鉴相器(以下简称PFD)的直流电动机控制方案在1973年第一次被提出，并且分析了其稳态精度达到0.01%的可能性。Tal首先建立了电压泵PFD的线性离散模型，并且从稳定性分析入手，得到了存在低速极限及其与环路参数的关系。20世纪80年代以来，随着电力电子、微电子技术以及控制技术的发展，对电动机调速系统性能的要求也越来越高，主要表现为：转速稳定精度高、动态调速性能好、抗干扰能力强等[3]。锁相调速虽然在稳态精度方面有独特的优势，但是在动态性能和抗干扰能力方面有明显的不足[4]，因此，对锁相环技术的研究主要针对这两方面。现代的电机锁相控制已发展成一个包括软硬件的控制系统，作为一种相位检测手段的锁相环技术，能够与其它先进的控制技术相结合，共同作用提高调速系统的综合性能[5-8]。

本文建立了锁相环稳速控制系统的动力学模型，首先采用环路参数模型参考自适应方法，改善锁相环系统的抗干扰性能，在此基础上设计了双模转速控制器。然后，基于协同控制理论对磁悬浮飞轮电机的转矩进行高动态、强鲁棒控制。最后对速率模式下磁悬浮反作用飞轮自适应锁相环协同控制方法进行了实验研究。

1 磁悬浮飞轮电机锁相环稳速控制系统模型

锁相环是频率和相位的同步控制系统，目的是实现输入参考信号和反馈信号的相等和相位差的恒定。利用锁相环技术能够实现数字信号的同步，将此策略融入到电机转速控制系统中，则可以实现转速控制中的高精度稳速控制。

电动机转速控制中应用的锁相环和通讯中应用的锁相环，两者之间有着根本上的差别。在电动机控制系统中，电机测速器通常作为有惯性的电压控制振荡器。锁相环转速控制(以下简称PLSC)系统主要由PFD、LPF及VCO等3个基本部件组成，其中，鉴相器是锁相环的核心元件。根据信号形式划分，锁相环可分为最初的模拟锁相环[9]、后继出现的数模混合锁相环[10]和各种不同性能的全数字锁相环路[11-13]，以及近几年出现的纯软件锁相环[14-15]。

文献[16]提出了一种基于PFD的锁相调速系统模型，并建立了PFD的非线性数学模型，但该模型中不包含转矩控制器，锁相环的动态响应特性较差。针对磁悬浮反作用飞轮工作在速率保持模式下，锁相环转速控制系统对转矩扰动的鲁棒性要求，本文引入了转矩控制器，以提高锁相环的动态响应速度和对转矩扰动的鲁棒性，控制系统的结构如图1所示。

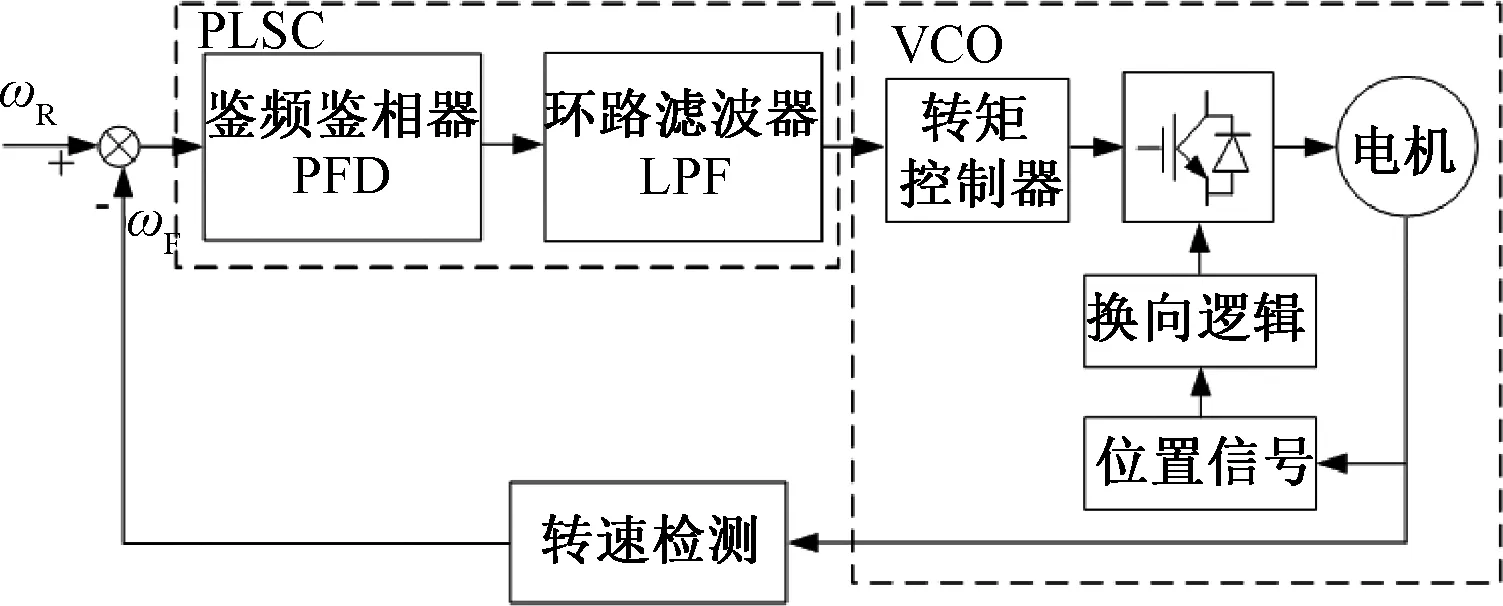
图1 锁相速度控制系统结构

PFD的输出通常表现为非线性，只有在锁相环靠近锁定的状况下能够表现出线性比例特性。在锁相调速系统中，电动机、转矩控制器和光电码盘共同组成带有惯性的VCO，电动机转速的输出通过霍尔传感器或者光电码盘转化为与电动机的转子转速成比例的脉冲信号，PFD比较参考输入脉冲信号与霍尔传感器或光电码盘输出的脉冲信号相位。

根据电动机的动态特性，锁相调速系统被认为比电子锁相环更高一级的系统。锁相调速系统在动态特性的性能和要求上与电子锁相环存在明显的差异，相较于电子锁相环，锁相调速系统频率低、时间常数大并且调速范围宽。电动机的机械惯量大，系统带宽变窄，系统时间常数比电子锁相环时间常数大，所以系统靠频率牵引作用入锁难度大。当磁悬浮反作用飞轮工作在速率保持模式下时，需对转速采用双模控制，双模控制系统的结构如图2所示。

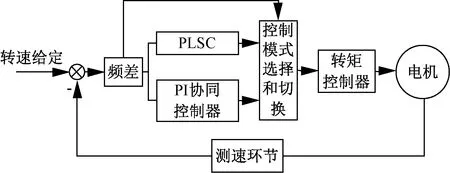
图2 双模锁相速度控制系统结构

如果系统转速误差的绝对值比设定的误差带大，则系统在转速PI协同控制作用下，电机迅速进行加速或者减速。当系统转速误差绝对值比设定的误差带小时，系统切换成锁相控制模式，系统处于稳定状态时只有锁相环控制作用，使系统获得较高的稳态精度。

假设磁悬浮飞轮电机三相对称，忽略换相转矩脉动的影响，则PLSC系统可用如下的微分方程组描述：

(1)

式中：F(θ,ω)=

式中：θ为相位差；ωR为参考信号频率；ω为电机输出转速；τd、τf为滤波时间常数；kp为PFD增益；Vc为滤波器输出；J为转子转动惯量；KT为飞轮电机转矩系数；Ke为飞轮电机反电动势系数；B为阻尼系数；Td为未补偿电机内扰动转矩；im为永磁无刷直流电机绕组相电流；Lm为绕组相电感；Rm为绕组相电阻；ΔVT为功率开关管通态压降；i为Buck DC-DC变换器的输入电流；Uo为Buck DC-DC变换器的输出电压；UDC为电源供电电压；L为Buck DC-DC变换器滤波电感；C为Buck DC-DC变换器滤波电容；u1为控制输入；N为码盘的刻线数或电机极对数与转子位置传感器数量的乘积。

PFD的输入/输出特性如图3所示。

图3 PFD输入/输出特性

2 锁相环自适应协同控制

采用双模转速控制是改善锁相环控制动态性能和扩大转速调节范围的有效途径[17-18]。双模转速控制避开了鉴相器的非线性工作区，不但具有良好的动态特性，还获得了较高的稳态精度。为了使双模控制系统从PI协同控制切换到锁相环控制后，环路能够快速入锁，就要求锁相环的快捕带大于误差带。此外，即使采用了双模控制，锁相环在飞轮电机内扰动转矩的作用下仍可能失锁[19-20]。当双模转速控制器运行于锁相控制方式时，系统结构见图2。在锁相环调速系统中引入转矩控制器，能够不同程度地改善环路的动态性能和抗干扰能力[21]。磁悬浮反作用飞轮在速率保持模式下，电机工作在正向或反向电动状态下。

定义状态向量x=(x1，x2，x3，x4，x5，x6)=(θ，Vc，ω，im，i，Uo)，则由式(1)所描述的微分方程组可得到锁相环系统的非线性状态空间模型：

(2)

因包含环路滤波器，所以在θ∈[0,2π]时，

F(x1,x3)=

k=0,1,2,…

(3)

2.1 正相位差时的锁相环自适应协同控制

当θ∈[0,2π]时，相差为正，锁相环的状态空间模型为线性。式(3)代入式(2)得到：

(4)

由式(4)可知，基于PFD的PLSC系统在θ∈[0,2π]时，相位误差在线性范围内。

环路的增益直接影响锁相环的稳速精度和带负载能力，增益增大则抗干扰的能力强，但稳态精度降低；增益减小则抗干扰的能力减弱，但稳态精度提高。在锁相环工作过程中，如果可以依据速度和相位误差的大小自动调整环路增益，则可以自动适应稳态精度和抗转矩扰动。在转矩控制器中引入协同控制器能够有效地提高转矩的动态跟踪能力。

磁悬浮反作用飞轮电机锁相环模型参考自适应控制器框图如图4所示。

图4 磁悬浮反作用飞轮电机锁相环模型参考自适应控制器

调节系统：

(5)

式中：θe为相位差。

参考模型：

(6)

式中：φe为相位差；KR为参考模型增益，在控制过程中不断更新。

采用模型参考自适应方法调节环路增益，当扰动转矩发生变化，飞轮电机的电磁转矩也相应改变来保证电机的稳定运行。常见的锁相环控制是控制增益恒定，通过相位误差的改变来调整转矩给定。而式(6)的参考模型定义了恒定的相位误差，通过调节环路增益，改变电磁转矩给定。

采用Lyapunov理论推导自适应律，选择Lyapunov函数：

(7)

式中：ξ为正常数。V对时间的导数：

(8)

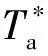
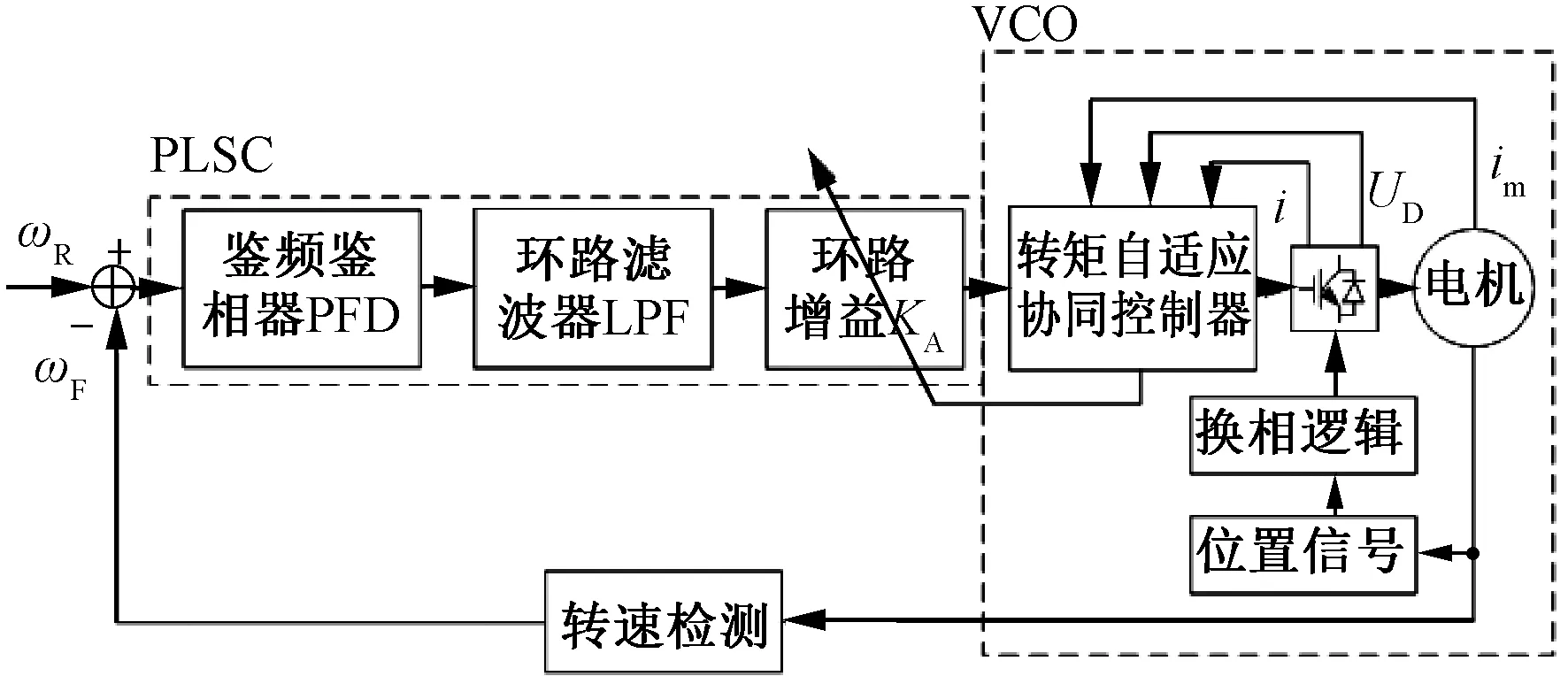
图5 锁相环自适应协同控制器框图

在转矩参考作用下，飞轮速率保持模式的转矩协同控制系统宏函数可定义为电机电磁转矩、Buck DC-DC变换器输入电流与其参考值的线性组合：

ψ1=k1(Ta-KAx2)+k2(x5-ir)

(9)

式中：k1和k2为权系数，Ta为飞轮电机电磁转矩的参考值；ir为Buck DC-DC变换器的输入电流参考值。定义流形的期望动态特性方程：

(10)

式中：趋近率T1是根据ψ1确定的，其决定了系统向流形面ψ1=0运动并且最终达到流形面的收敛速度。

飞轮电机的电磁转矩：

Ta=KTim

(11)

将式(11)代入到(10)得：

k1(KTim-KAx2)+k2(x5-ir)=0

(12)

将式(4)代入式(12)中，得到飞轮加速运行的协同控制律：

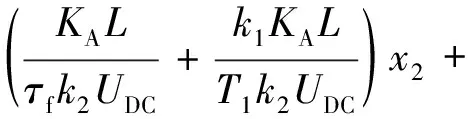
(13)

式(13)构成磁悬浮反作用飞轮电机速率保持模式的锁相环转矩协同控制规律。

2.2 负相位差时的锁相环自适应协同控制

当θ∈[-2π,0)时，相差为负，锁相环的状态空间模型是非线性的。

(14)

由式(14)可知，基于PFD的PLSC系统在θ∈[-2π,0)时，虽然相位误差在线性范围内，但PFD的输入/输入特性仍具有强非线性。

在快捕带内，锁相环的参考转频和反馈转频同步，因此可将式(14)的状态空间模型转换：

(15)

当θ∈[-2π,0)时，锁相环的模型参考环路增益自适应控制与θ∈[0,2π]时的算法相同。在转矩参考作用下，飞轮速率保持模式的转矩协同控制系统宏函数仍定义为式(9)的电机电磁转矩、Buck DC-DC变换器输入电流与其参考值的线性组合。

将式(14)代入式(12)中得到：

(16)

式(16)构成磁悬浮反作用飞轮电机速率保持模式的锁相环自适应协同控制规律。

3 实验验证

3.1 基于FPGA的全数字锁相环设计

鉴相器通常被划分成两大类，第一类为乘法器(或称组合逻辑电路)，第二类为时序电路。第一类鉴相器的输出是信号的输入波形和本地振荡器的波形做乘后所得乘积的平均值。第二类鉴相器输出的有用误差电压仅根据输入信号波形的翻转与磁悬浮飞轮电机转速波形的翻转两者之间的时间间隔决定，与其他信息无关。

在电机锁相环转速控制系统中，最重要和最著名的时序鉴相器是PFD，本文采用的PFD模型如图6所示，模型由两个D触发器、一个与门和一个接在反馈回路中的延迟组成。D触发器的数据端始终接逻辑高电平。两个D触发器的时钟端输入分别为参考转速的翻转和反馈信号的翻转。两个D触发器的输出一个标记为OUP，另一个标记为ODN。正确极性的时钟沿把它与相连的D触发器置1。当与门判断出OUP和ODN同时为真时，通过反馈把两个D触发器同时置0。PFD的时序逻辑采用FPGA实现。

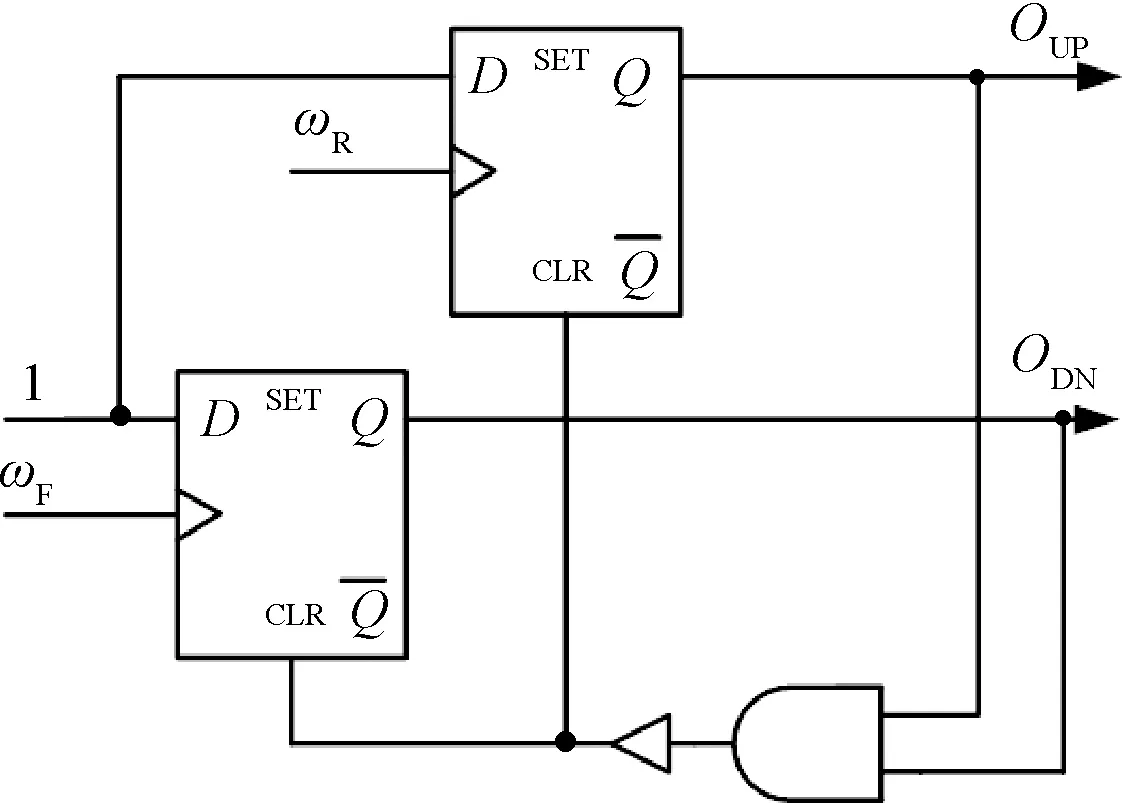
图6 锁相环的PFD

OUP的有效输出反馈转速相位滞后于参考信号，ODN的有效输出反馈转速相位超前于参考信号。OUP和ODN的有效输出指出了相位误差的方向。而相位误差的大小则由OUP和ODN脉冲的宽度来确定，PFD的波形如图7所示。

图7 锁相环的PFD

在通常情况下，PFD发挥着驱动电荷泵的作用，电荷泵的作用是在每个相位比较周期区间，根据相位误差配给环路滤波器相应的电荷量。基于电荷泵的锁相环的PFD输出是包含在OUP和ODN脉冲的宽度里面的，而脉冲宽度是连续变化的模拟量。因此，采用PFD和电荷泵组合结构的锁相环仍然是模拟锁相环，而不是数字锁相环。

本文采用可逆计数器代替锁相环中的电荷泵，将可逆计数器的输出进行数字积分，并把双模控制切换前的PI协同控制器的输出与可逆计数器数字滤波后的输出求和，作为锁相环的控制量输出。自适应算法和协同控制算法在FPGA中做数值运算，自适应协同控制的输出量与载波比较生成PWM。

3.2 实验验证

磁悬浮反作用飞轮工程化实验验证平台如图8所示。实验平台包括28 V直流电源、15 N·m·s磁悬浮反作用飞轮、飞轮电机磁轴承控制系统、飞轮电机数字控制系统等，霍尔转子位置传感器提供磁悬浮飞轮的转速信息。磁悬浮反作用飞轮的主要技术指标如表1所示。

图8 磁悬浮飞轮实验平台

表1 磁悬浮反作用飞轮主要技术指标

在磁悬浮反作用飞轮速率保持模式的锁相环自适应协同控制下，锁相环系统在捕获带内不同频率下的环路滤波器输出波形如图9所示。给定参考转频666 Hz，图9(a)是反馈转频滞后时的环路滤波器输出波形，图9(b)是反馈转频超前时的环路滤波器输出波形。

图9 锁相环环路滤波器的输出

图10是在随机扰动转矩作用下锁相环自适应协同控制系统电流的动态响应。

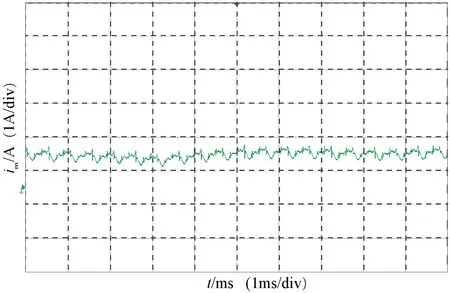
图10 电流的动态响应

图11是磁悬浮反作用飞轮在速率保持模式下的锁相环自适应协同控制系统稳速曲线，飞轮电机的转速稳定度优于1×10-4。

4 结 语

本文首先建立锁相环稳速控制系统的动力学模型，采用环路参数模型参考自适应方法，以保证在扰动转矩作用下仍能维持较高的稳速精度。然后，基于协同控制方法设计了磁悬浮飞轮电机的高动态转矩控制器，提高了锁相环的响应速度和抗扰动能力。设计了基于FPGA的数字锁相环自适应协同控制器，在FPGA控制器上实现了锁相环自适应协同控制算法，最后对磁悬浮反作用飞轮速率保持模式锁相环自适应协同控制方法进行了实验研究。