定子齿顶开槽减小开关磁阻电机振动和噪声分析
2021-09-02黄朝志段锦锋周满国
黄朝志,段锦锋,周满国,谢 威
(江西理工大学 电气工程与自动化学院,赣州 341000)
0 引 言
开关磁阻电机(以下简称SRM)以其结构简单、功耗小以及低速大转矩等诸多优点,在许多领域表现出广阔的应用前景,目前已广泛应用于纺织、冶金、交通运输等行业[1]。然而,由于双凸极结构、非线性磁饱和特性以及定转子间周期性的径向电磁力导致定子发生形变,SRM在工作过程中会产生较大的振动和噪声,这个缺点对电机自身的功能造成一定的影响,同时也限制了其在许多噪声敏感领域的应用[2-3]。因此,从电机本体结构出发抑制SRM的振动噪声成为该领域的研究热点[4-6]。
SRM产生振动噪声的主要原因是定子的振动,转子位置角变化和绕组电流通断产生的周期性径向力使定子和转子不断发生相对运动,使得SRM定子发生形变[7]。迄今为止,关于SRM的振动噪声研究主要集中在控制领域。基于转矩分配[8]和直接转矩控制[9]的方法可使得SRM的电磁转矩更为平稳光滑;电流双限幅斩波控制方式在SRM低速运行时可有效降低振动和噪声[10]。这些控制方法都增加了控制器和控制方法的复杂性,使电机的制造成本增加。近年来,国内外专家也开始重视基于电机本体结构来降低SRM的振动和噪声。文献[11-12]通过改变SRM定子和转子的结构来减小转矩脉动,文献[13-14]研究了SRM定子结构对振动和噪声的影响,文献[15]研究了不均匀气隙对SRM振动和噪声的影响,文献[16]研究了定转子斜槽对单相SRM振动和噪声的影响。这些基于本体的方法大多适用于特殊场合,通用性不强且电机的制造成本高。在SRM多场耦合对振动的分析研究中,文献[17-19]建立了SRM定子的有限元分析模型,并分析计算出定子没有任何约束时的自由振型和固有频率;文献[20]研究了机壳、绕组、端盖等因素对SRM的振动模态的影响;文献[21]分析了双定子SRM的机械振动以及振动噪声。
本文从SRM本体结构出发,研究了一种结构简单、制造成本低的新型定子结构,通过改变定子结构来改变定子表面的磁密方向,削弱径向磁密,增大切向磁密,从而削弱了SRM径向力,通过多场耦合仿真分析,得到传统定子和开槽定子的固有频率、振动响应频率以及声压,仿真结果验证了开槽定子对抑制SRM振动噪声的有效性。
1 SRM定子齿顶开槽的原理分析
SRM工作时,定转子间周期性的电磁力可导致定子发生形变,是SRM振动和噪声的主要原因。电磁力分成径向电磁力和切向电磁力,径向电磁力是产生振动的主要因素,若能减小径向电磁力,SRM振动和噪声也会有效降低。本文在定子极顶开槽,增大了该位置气隙磁阻,产生了开槽效应,使得本该垂直进入转子磁极的磁力线被挤压到磁阻更小的未开槽区域,而原来该区域的磁力线被挤压到定子齿外,这样可以减小径向电磁力,从而削弱SRM振动噪声。
根据虚位移公式[22],得到SRM径向力表达式:
(1)
式中:W′m是磁共能,g是气隙长度。当磁路为线性时,磁化曲线是一条直线,电机内部的磁场储能和磁共能刚好相等,故磁共能可表示:
(2)
式中:i是绕组电流,N是线圈匝数,磁导Λ=1/Rm,磁阻Rm的表达式:
(3)
式中:μ0是真空磁导率,S是定转子的重叠面积。当电流i恒定时,整理式(1)~式(3),得到径向力表达式:
(4)
式(4)中,S=lstkrθ=lstkt,气隙长度g和重叠长度t影响径向电磁力,即径向电磁力随着定子齿和转子齿重叠面积的增大而增大,当定子和转子完全重叠时,其径向力达到最大。负号是因为气隙长度g和径向电磁力Fr呈负相关,适当增大气隙长度g,则可以减小径向电磁力。
根据图1参数计算,得到传统定子和开槽定子径向力Fr1和Fr2:
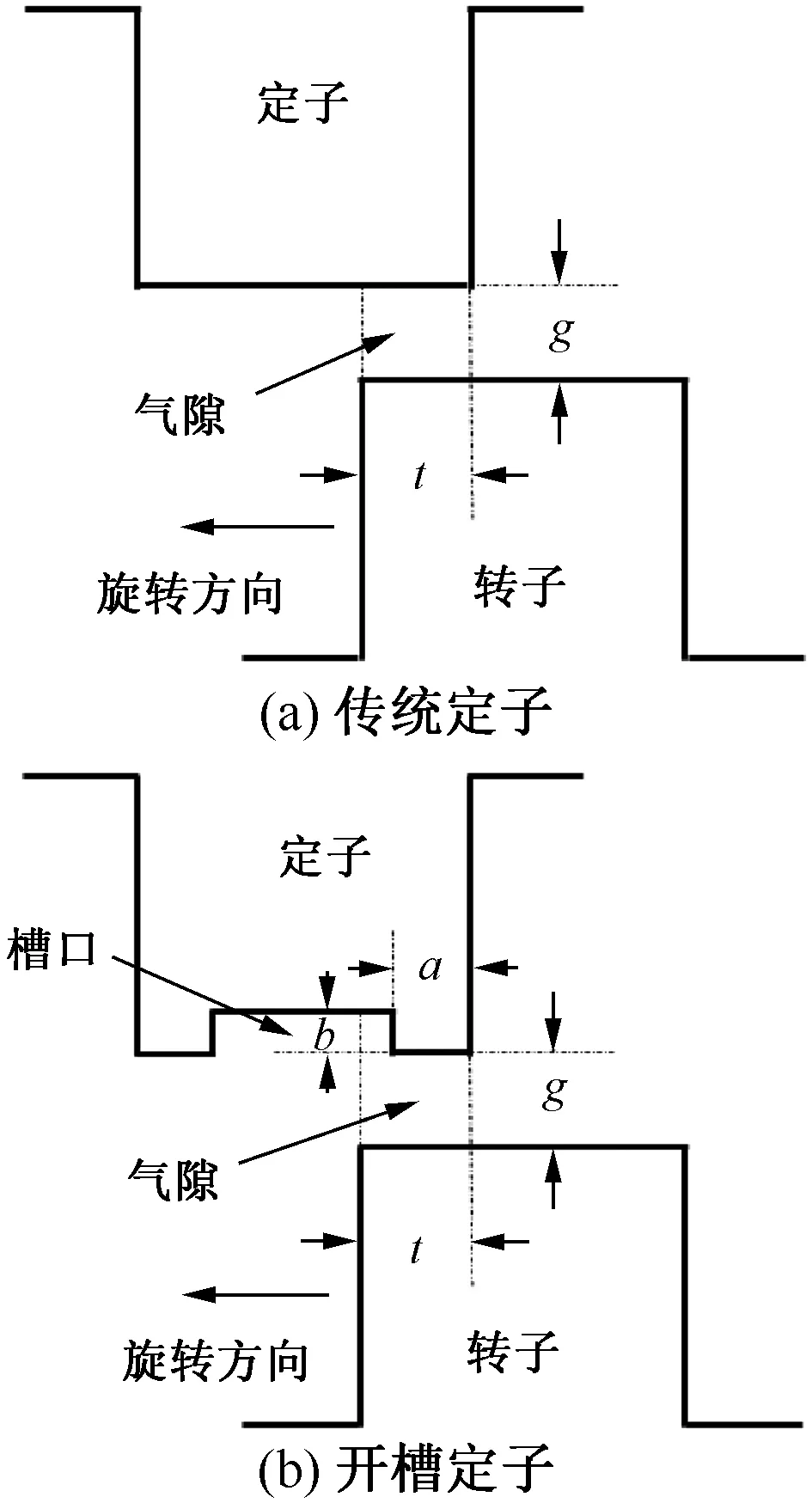
图1 传统定子与开槽定子的分析
(5)
(6)
整理式(5)、式(6)得:
(7)
由式(7)可知,定子开槽后径向力比未开槽时明显要小,故通过定子齿顶开槽可以有效降低径向力,从而改善SRM振动噪声。
2 定子极开槽的径向力分析
2.1 模型参数
本次研究选取12/8极对数的SRM作为研究对象,额定电压280 V,额定功率2.2 kW,额定转速3 000 r/min,工作温度75 ℃,研究了不同槽口尺寸对径向力的影响,确定最优开槽参数。电机主要参数(开槽参数除外)如表1所示。
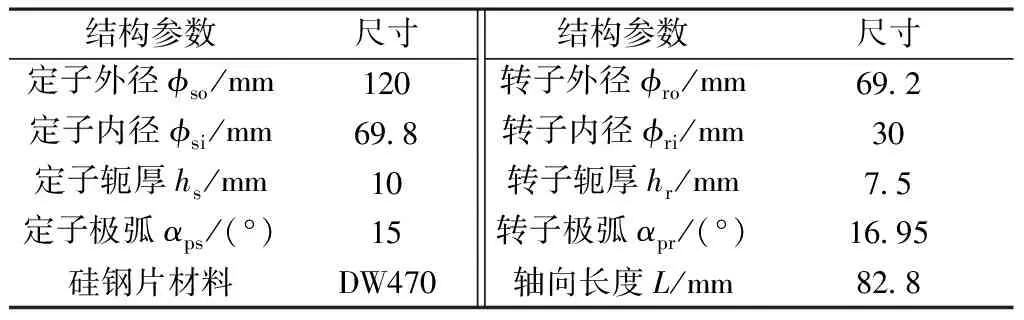
表1 SRM的主要参数
依据表1中的电机参数,本文建立的SRM几何模型,如图2所示。
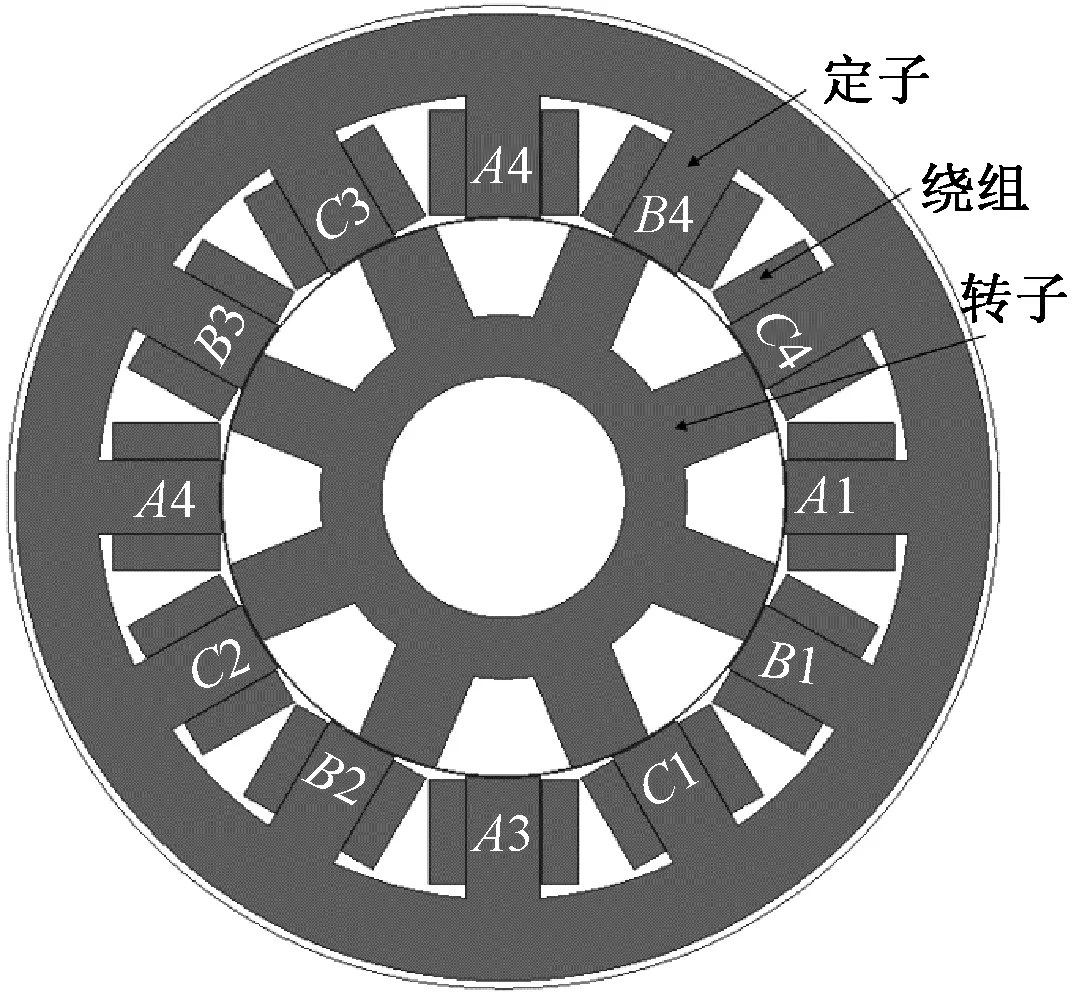
图2 SRM几何模型
2.2 SRM定子极开槽参数的优化
选择在定子齿顶中间开一个宽度w为0.5 mm、深度d为3 mm的矩形槽,如图3所示。

图3 定子齿顶开槽
因为SRM遵循最小磁阻原理,即当转子极轴线和定子极轴线重合时磁阻最小,磁密最大,所以选取断电时刻进行分析,得到径向磁密、切向磁密,如图4所示。对比可知,开槽定子的径向磁密峰值降低了29.6%,切向磁密峰值增加了39.4%。

图4 磁密分布
根据麦克斯韦张量法[23],径向力波表达式:
(8)
式中:Br为径向磁密;Bt为切向磁密;μ0为真空磁导率。
由式(8)可知,可以通过减小径向磁密、增大切向磁密的方法来降低径向力波。定子开槽前后的径向力波与径向力,如图5所示。由图5可知,开槽定子的径向力波和径向力降低较明显,径向力波降低了8.2%,平均径向力降低了5.7%。
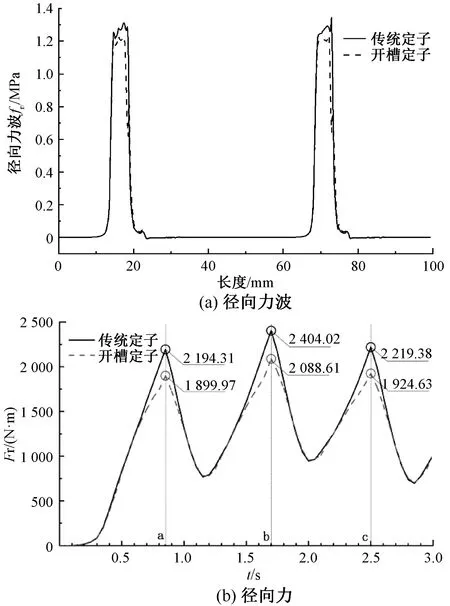
图5 径向力波与径向力
先保持深度为1 mm不变,槽宽为0起,以0.5 mm为梯度逐次增加,对不同开槽宽度模型进行有限元分析。
由图6可以看出,随着开槽宽度的增加,平均转矩和径向力波呈线性递减,但槽口不宜过宽,否则不仅会使得平均转矩大幅减小,而且会导致漏磁增加,造成切向磁密减小。通过比较分析,选择0.5 mm为最佳开槽宽度。
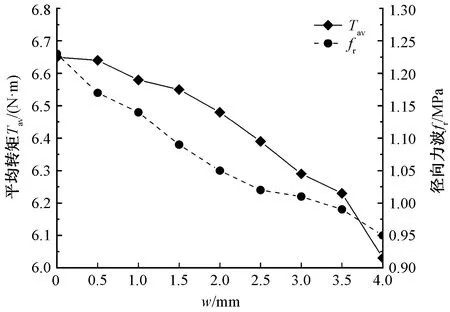
图6 不同开槽宽度的平均转矩和径向力波
选定0.5 mm为最佳槽口宽度后,对不同槽口深度模型进行有限元分析,深度为0起,以0.5 mm为梯度依次递增至4 mm,观察平均转矩和径向力波的变化。
由图7可以看出,随着开槽深度的增加,平均转矩略微下降,径向力波下降明显,开槽深度在3 mm至4 mm时,平均转矩和径向力波变化不明显。综合分析,确定3 mm为最优开槽深度。
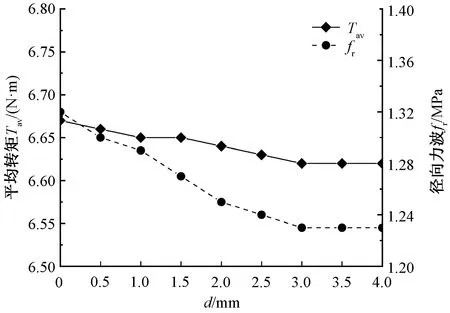
图7 不同开槽深度的平均转矩和径向力波
由以上仿真分析可得,在定子齿顶开一个宽0.5 mm、深3 mm的矩形槽,优化后定子结构径向力波峰值下降了8.2%,平均径向力下降了5.7%,表明合适的开槽尺寸可以有效减小径向力,从而抑制电磁振动。
3 SRM的振动分析
3.1 振动仿真流程
SRM振动噪声仿真流程,如图8所示,先将Maxwell中的定子齿进行分离,并对分离出的定子齿网格加密处理,以得到更准确的电磁力密度,经过计算得到定子齿部电磁力,然后把定子齿部电磁力作为激励源,使电磁力加载到三维定子齿部,得到振动响应,同时结合模态分析,得到定子固有频率,最后把谐响应分析的振动速度加载到空气域内表面,得到声压频谱。
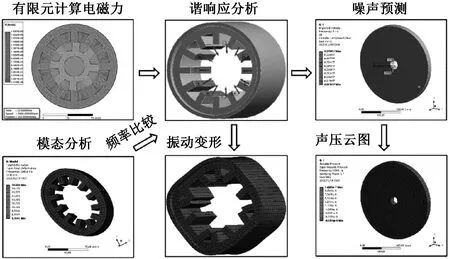
图8 振动及噪声分析流程
3.2 SRM定子铁心模态仿真
模态分析是研究结构体力学特性的方法,不仅可以得到结构体较准确的固有频率值,还能显示出不同阶的振动模态[24]。本文在Workbench中对传统定子和开槽定子进行模态分析,得到两模型固有频率和各阶振型,从而可以在本体结构设计中避免受迫响应频率与固有频率趋于一致而引起共振现象。本文定子材料是50W470型号的硅钢片,其主要参数如表2所示。

表2 定子材料参数
考虑到定子铁心是硅钢片叠压而成的,用材料密度与叠压系数之积作为实际仿真的材料密度,目的是提高仿真的精确度。图9为传统定子和开槽定子的三维模型。
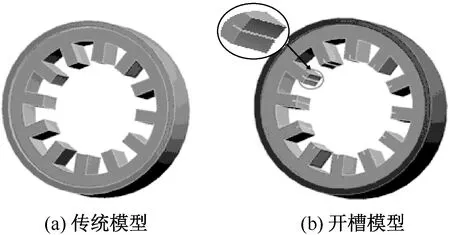
图9 三维定子模型
分析SRM定子前12阶模态,由于定子铁心是无约束条件的自由振动,前6阶固有频率几乎为0,故本文将第7阶模态作为第1阶模态,依此类推。传统定子与开槽定子第1阶~第6阶模态所对应的固有频率如表3所示,不同阶次下的振型如图10~图15所示。可见,定子振型呈规律性变化。
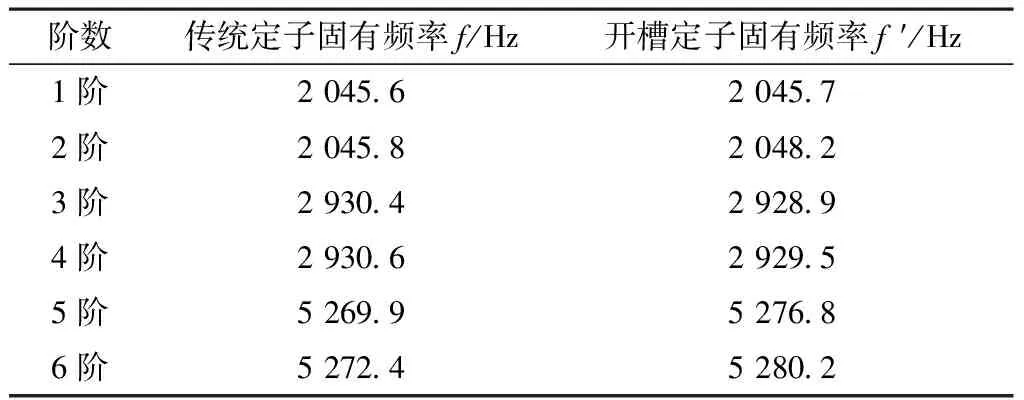
表3 不同阶次的固有频率
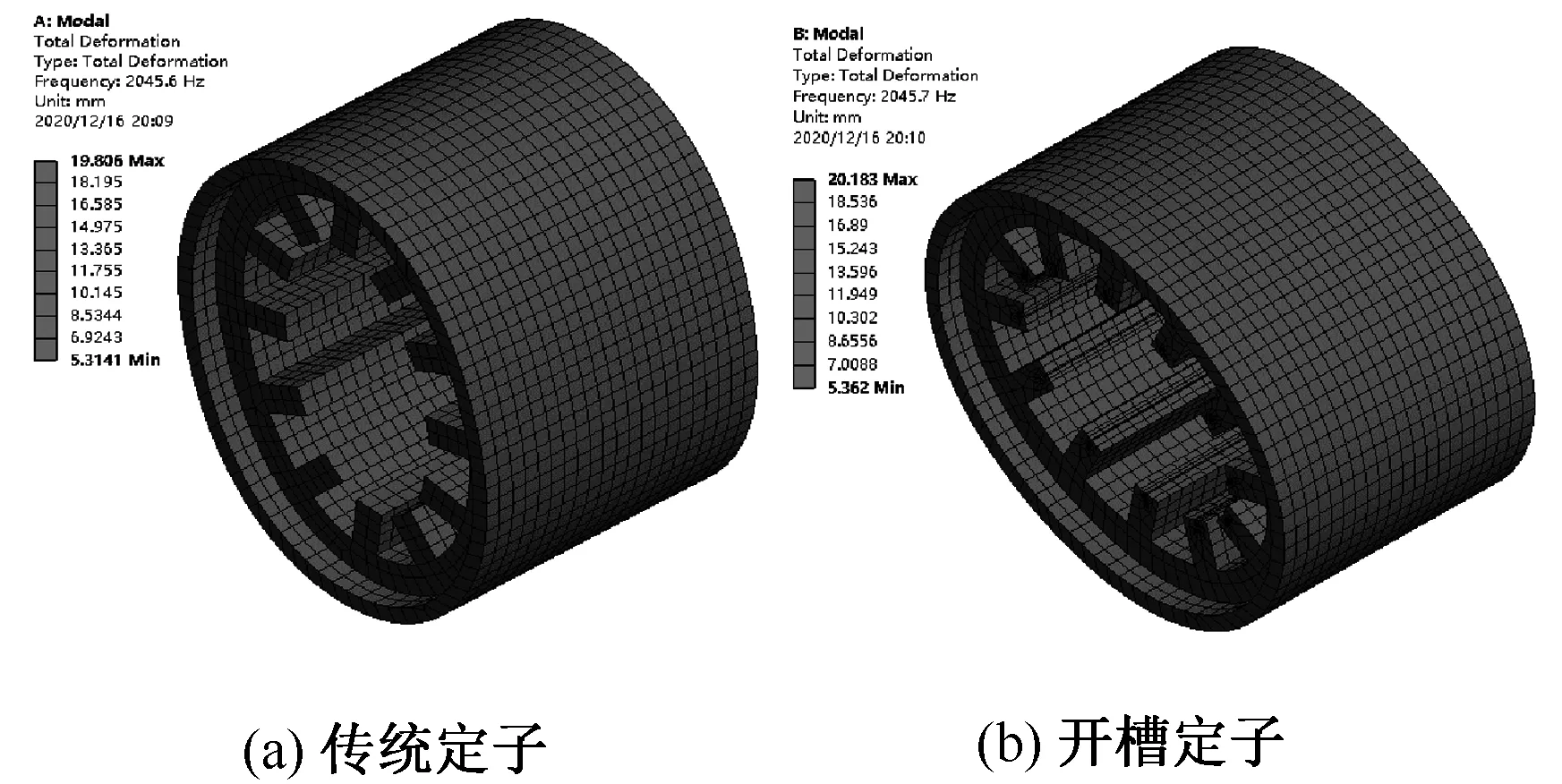
图10 传统定子与开槽定子1阶振型
图11 传统定子与开槽定子2阶振型
图12 传统定子与开槽定子3阶振型
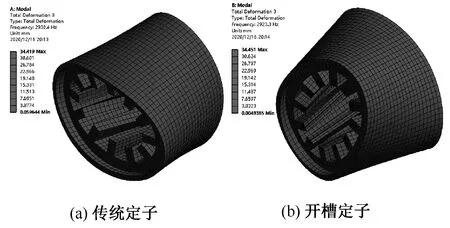
图13 传统定子与开槽定子4阶振型
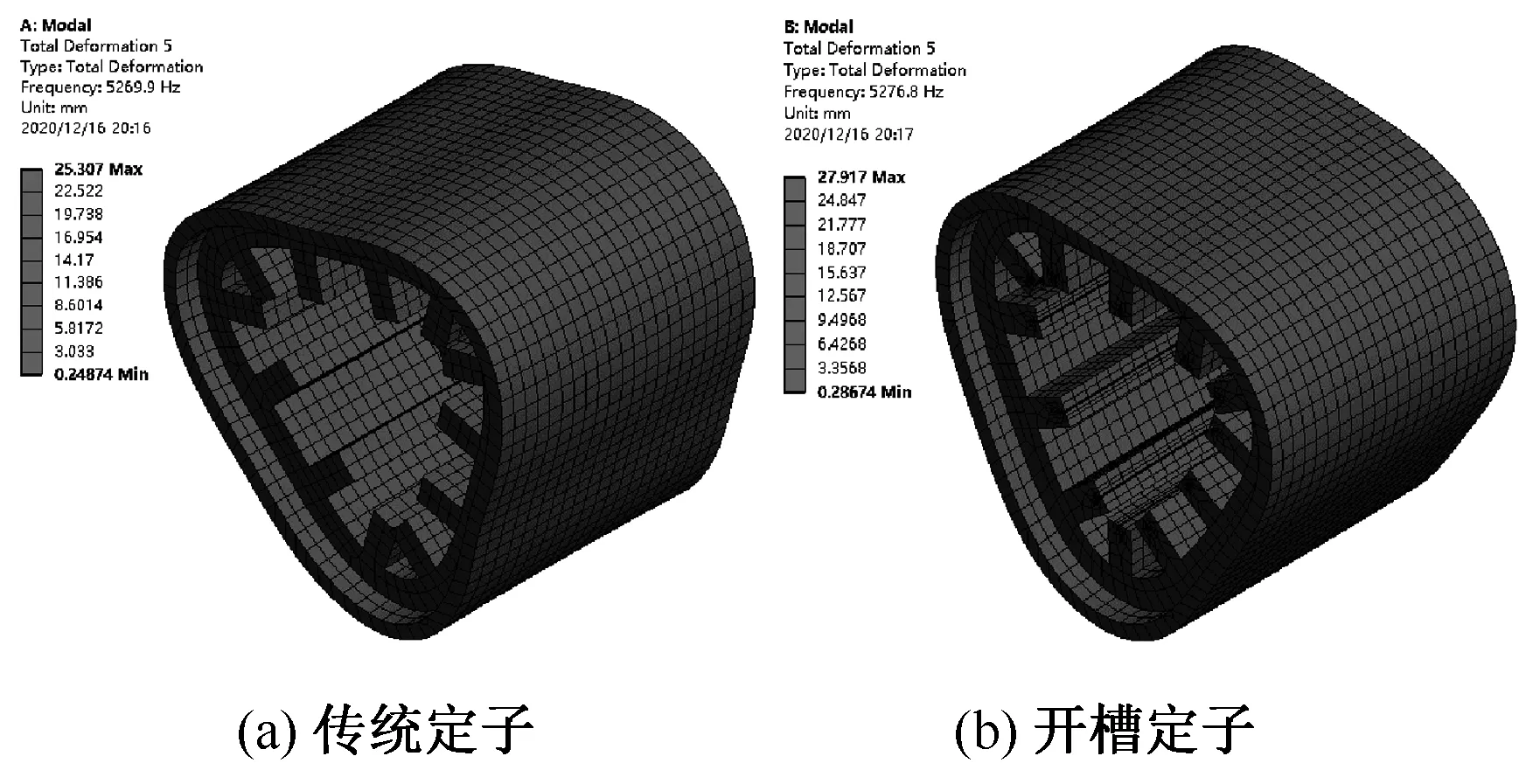
图14 传统定子与开槽定子5阶振型
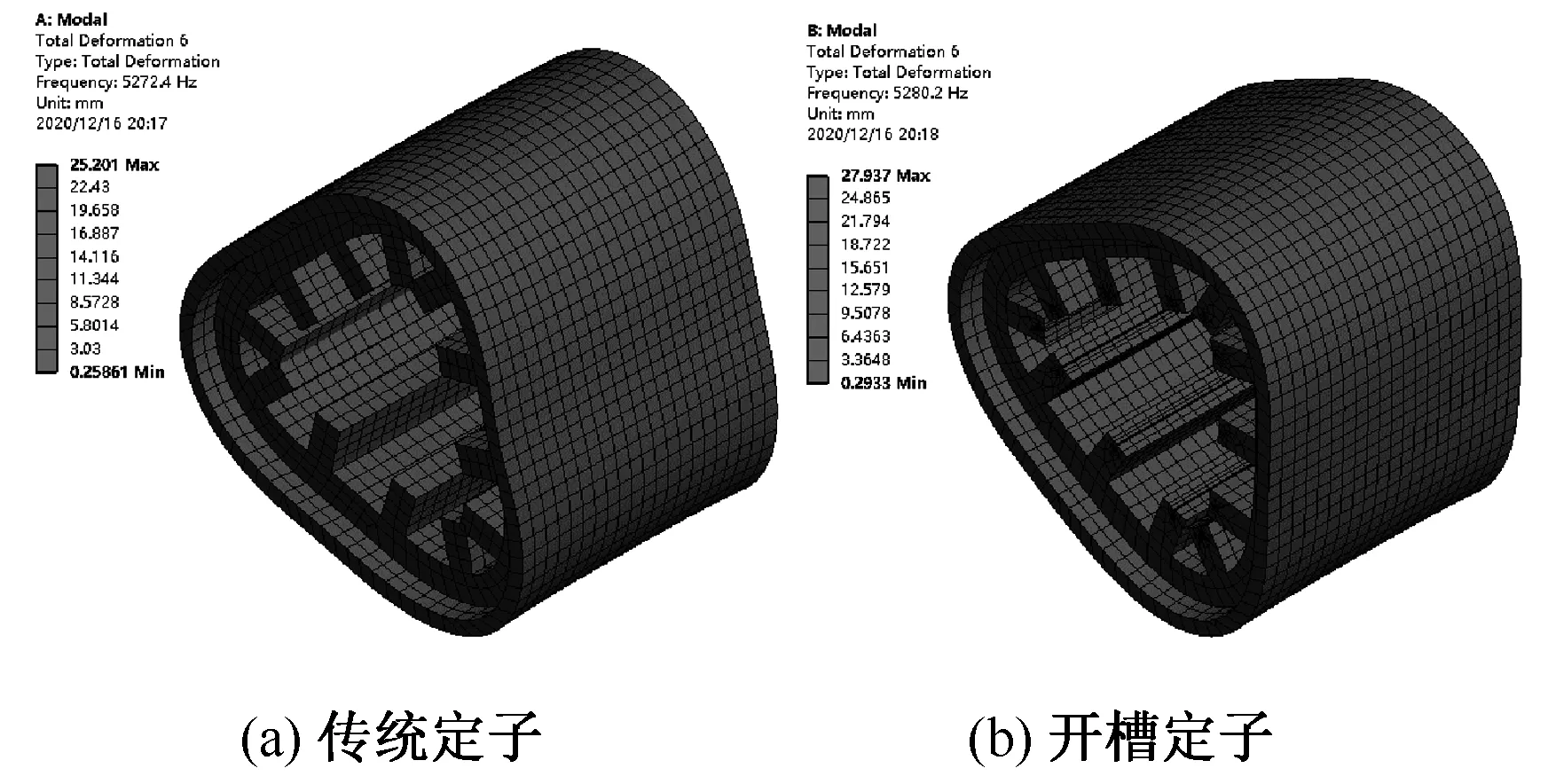
图15 传统定子与开槽定子6阶振型
3.3 SRM谐响应仿真分析
谐响应分析是在频率不同的正弦载荷作用下结构体响应的分析方法,其目的是探测结构体在不同频率下的振动响应,避免与结构体的固有频率一致而出现共振。将电磁力作用点置于定子齿中心,传统定子和开槽定子电磁力耦合如图16所示。

图16 径向电磁力的分布
在径向电磁力的激励下,得到传统定子和开槽定子在0~6 000 Hz范围内的振动位移、振动速度和振动加速度的频率响应曲线,如图17所示。
由图17分析比较可得,开槽定子比传统定子的振动位移幅值降低了60.3%,振动速度幅值和振动加速度幅值降低了20%。结果表明,定子开槽可有效降低SRM振动。
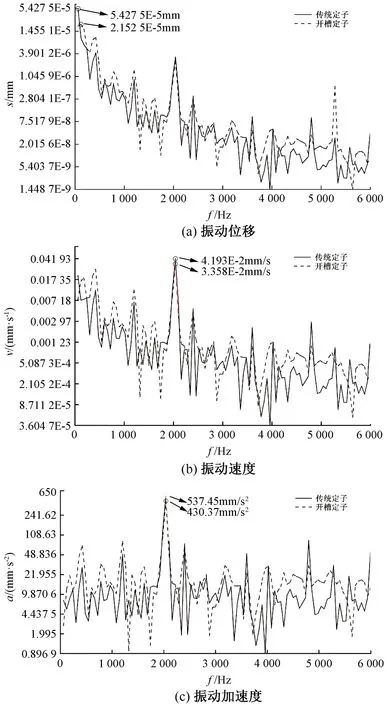
图17 定子振动频率响应
3.4 SRM的噪声预测
SRM的噪声主要是定子径向振动引起的,故本文建立10倍于定子外径的空气域,将谐响应分析的振动速度加载到空气域内表面,如图18所示。

图18 空气域
在振动速度的激励下,得到传统定子和开槽定子的声压频谱。
由图19分析可得,开槽定子SRM的声压明显低于传统定子SRM,声压峰值降低了50.2%。
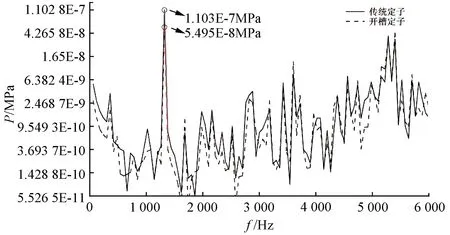
图19 噪声声压频谱
4 结 语
本文分析了SRM产生振动噪声的主要原因,研究了一种新型定子结构,该结构是在传统定子齿顶开一个深3 mm、宽0.5 mm的矩形槽。通过对SRM电磁分析,得到瞬态电磁力密度,再对传统定子和开槽定子进行多物理场分析,得到以下结论:
(1) 比较分析了两种定子结构,结果表明,定子开槽可有效降低SRM的径向力波和径向力,可以有效改善SRM振动特性。
(2) 通过对传统定子和开槽定子的模态和谐响应分析,得到两者的固有频率和受电磁径向力后的频率响应,得知响应频率与固有频率在2 000 Hz附近趋于一致,故会引起共振现象。
(3) 多物理场耦合结果表明,开槽定子振动噪声较传统定子有明显改善,这种定子齿顶开槽的方法对研究其他双凸极电机振动噪声有借鉴意义,且易于实现。
