6063-T5铝合金热变形行为及热加工图研究
2021-09-02洪浩洋杜向阳颜志刚
洪浩洋,杜向阳,颜志刚
上海工程技术大学 机械与汽车工程学院,上海 201620
0 引言
铝合金因密度较低、比强度较高、耐腐蚀性良好等优异性能,在航空航天、汽车和船舶零部件的制造中备受青睐[1-3].其中6xxx系列铝合金相比2xxx和7xxx系列铝合金性价比更高、耐腐蚀性更好、更易加工,应用也更为广泛[4].6063铝合金是6xxx系列铝合金中应用最广泛的一种,其供货状态一般为T5[5].为满足我国制造业对铝合金材料塑性加工性能的要求,研究发现[6-7],金属材料在塑性加工过程中的流变行为十分复杂且对塑性加工性能具有重要影响.变形温度、应变速率等热变形参数及材料的热处理状态都会引起流变行为变化,而这些变化主要是由材料的微观组织变化所致[8-9].
目前,对于6xxx系列铝合金流变行为的研究主要是通过分析金属材料热变形行为,建立本构模型,绘制热加工图获得热加工工艺参数,从而达到提升材料塑性加工性能的目的.高俊[10]通过对6082铝合金(温度区间为350~500 ℃)不同应变速率下的热变形行为进行研究,将建立的Arrhenius本构模型用于有限元模拟中,并使用热加工图为工艺分析提供数据支持.刘建勃等[11]通过研究Al-0.62Mg-0.73Si合金(温度区间为400~520 ℃)不同应变速率下的热变形行为,为研究该铝合金材料的热压缩行为提供了Arrhenius本构模型.叶文宏[12]通过研究6A02铝合金(温度区间为410~450 ℃)不同应变速率下的热变形行为,建立了Arrhenius本构模型与Johnson-Cook本构模型,通过对比两模型发现Arrhenius本构模型更加准确.L.Chen等[13]通过对6026铝合金(温度区间为400~550 ℃)不同应变速率下的热变形行为进行研究,建立了修正的Johnson-Cook本构模型与Arrhenius本构模型,并指出,为了更精确地描述材料流变行为,应该在Arrhenius本构模型中引入应变对材料常数的影响.Y.C.Huang等[14-15]分别对6063铝合金(温度区间为300~500 ℃与300~450 ℃)不同应变速率下的热变形行为进行了研究,并根据热加工图确定了热加工工艺参数.
综上可知,对于相同材料,不同的合金成分会造成不同的分析结果,且目前对于6xxx系列铝合金的流变行为研究主要集中在建立不同合金成分下的本构模型与绘制热加工图.对于T5热处理后的6xxx系列铝合金的热变形行为及基于材料热变形行为建立描述微观尺度位错密度增长模型的研究较少.因此,本文拟使用热模拟实验机对6063-T5铝合金进行轴对称等温压缩实验,建立自适应系数Arrhenius本构模型和位错密度增长模型,并通过绘制热加工图考查热加工工艺参数对6063-T5铝合金热变形行为的影响,以期为分析材料的塑性成形性能提供参考.
1 轴对称等温压缩实验
1.1 主要材料与仪器
主要材料:国标6063-T5铝棒,由银泰金属材料有限公司提供.
主要仪器:Gleeble-3800型热模拟压缩机,美国Dynamic Systems Inc产.
1.2 实验方法
将经机械加工的表面光滑的6063-T5试样进行热电偶焊接,以便在热压缩过程中测量试样的温度场变化,通过热电偶反馈调整PID以实现温度的准确控制.将处理好的试样放入热模拟压缩机实验舱进行实验.考虑到铝合金材料的熔点温度为616~654 ℃,本次实验设置变形温度分别为225 ℃、300 ℃、375 ℃、450 ℃、525 ℃,应变速率分别为0.01 s-1、0.1 s-1、1 s-1.具体步骤为:首先,试样以5 ℃/s的升温速度加热至变形温度并保温3 min;然后,以不同应变速率进行压缩变形;最后,当变形量达到真应变为1时停止压缩,并立即水淬.
1.3 实验结果分析
图1为6063-T5铝合金在不同变形条件下的真应力-真应变曲线图.由图1可以看出,每条曲线的整体变化趋势基本一致,都是在变形开始后,真应力随着真应变的增加显著增大,当真应力达到峰值后趋于稳定.这表明,在真应变未达到某一临界值时的开始阶段,加工硬化占据主导地位,而在真应变到达某一临界值后,材料的某种软化机制效果逐渐增大,并在与加工硬化现象相互抵消中达到一种动态平衡.对于低应变速率(应变速率≤1 s-1)情况,6063系列铝合金的加工硬化主要是位错密度增长,而软化机制主要是动态回复与再结晶[15].
流变行为即材料在塑性变形过程中真应力的变化情况,是表征材料性能的重要参数,它不仅与材料本身性质有关,还与工艺参数关系紧密.由图1可以看出,当真应变为0.5后,真应力基本趋于稳定,因此取真应变为0.5时的数据分析工艺参数对真应力的影响更为直观.但在实际测量数据中,会出现数据点不连贯的现象,对此本文采用3次样条插值的方法获得缺少的数据值.

图1 6063-T5铝合金在不同变形条件下的真应力-真应变曲线Fig.1 True stress-true strain curves of 6063-T5 aluminum alloy under different deformation conditions


图2 不同变形条件下真应变为0.5时的真应力值Fig.2 True stress value of true strain 0.5 under different deformation conditions
由图2b)可以看出,随着应变速率的升高,真应力呈缓慢上升趋势,其中当应变速率为0.01 s-1时,真应力最低,当应变速率为1 s-1时,真应力最高.这主要是因为:一方面,应变速率提升,材料塑性变形时间缩短,位错运动更加困难,造成了位错的交割与堆积,平均位错密度升高;另一方面,应变速率的提升导致了再结晶过程所需的长大时间过短,从而出现不完全再结晶的现象.

2 6063-T5铝合金本构关系模型的构建
在热变形过程中,材料的真应力依赖于变形温度与应变速率.鉴于这种依赖关系,本文采用文献[16-17]提出的包含再结晶变形激活能Qact与变形温度T的Arrhenius模型,如公式①、②与③所示,再根据文献[18]的研究成果,应变速率与温度T之间的关系可用Z参数表示,如公式④所示.
①
②
③
④
式中,A1、A2、A、n1、n、β、α为材料常数,R为摩尔气体常数值8.314 J/(mol·K),T为绝对温度.由公式④可得真应力计算公式如下.
⑤
⑥
式中,a0,a1,a2,…,an、b0,b1,b2,…,bn、c0,c1,c2,…,cn、d0,d1,d2…,dn为拟合系数.
2.1 材料常数的求解
关于材料常数的求解,可以使用由峰值应力求得的Z参数进行建模[19-22],也可以使用由峰值应力求得的Z参数建立双曲正弦模型作为真应力本构模型[23].H.J.Mcqueen等[24-26]也指出,当使用峰值应力求解Qact时,虽然会使激活能值更大一些,但能弥补实际生产中环境波动造成的误差,使结果更加准确.许多学者[19-22]使用通过峰值应力求解的材料常数进一步建立微观组织模型,获得了准确的计算结果,也验证了H.J.Mcqueen的说法.因此,对于材料常数的求解转变为峰值应力下材料常数的求解.

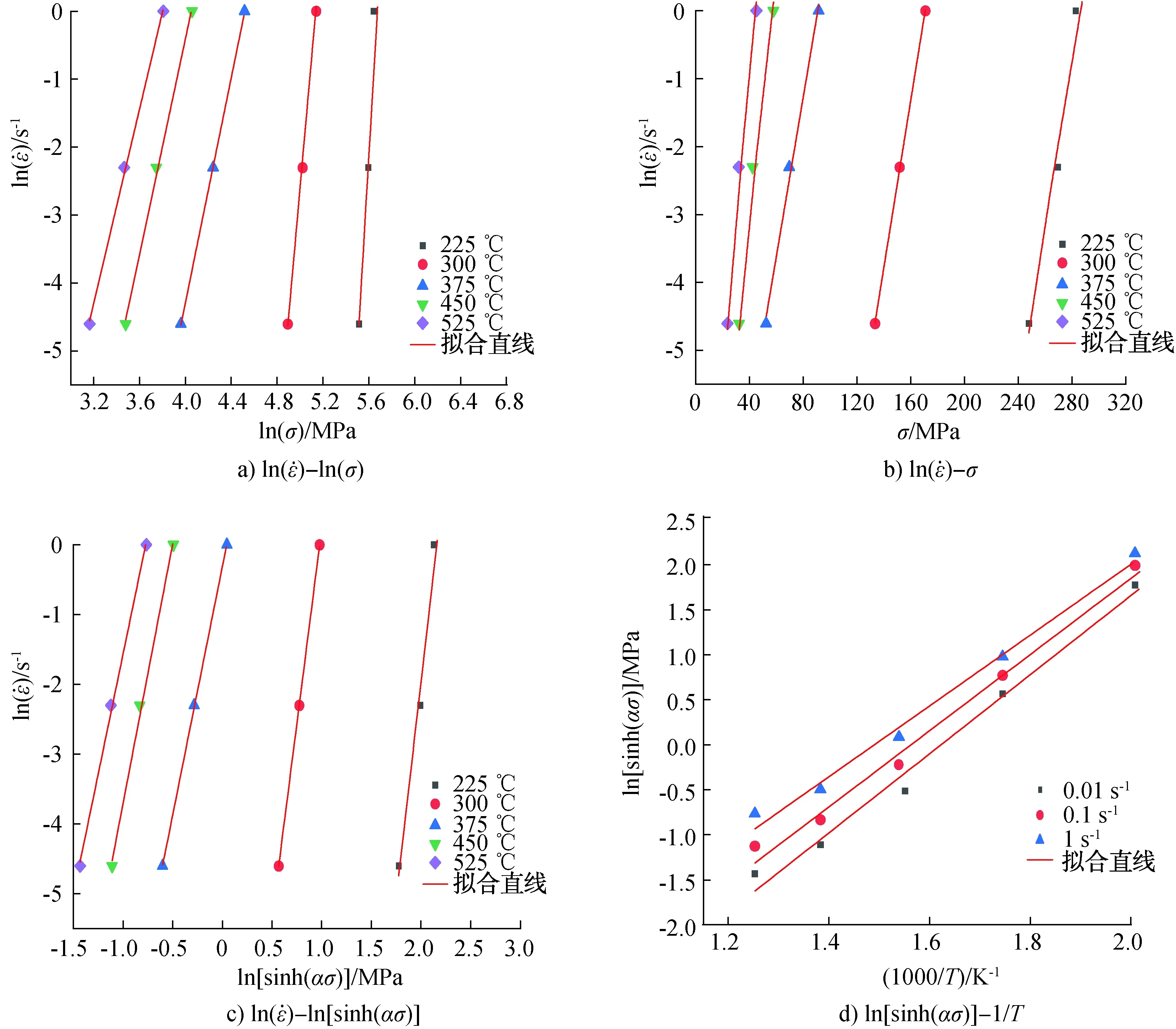
图3 实验值拟合关系曲线Fig.3 Experimental value fitting relation curves
ln(Z)=ln(A)+nln[sinh(ασ)]
⑦
图4为Z参数与峰值应力关系,其中拟合曲线的截距为57.174 686,则通过上述过程即可求得峰值应力材料常数,其中α=0.009 981,n=9.090 846,A=6.771×1024,Qact=316.714 kJ/mol.
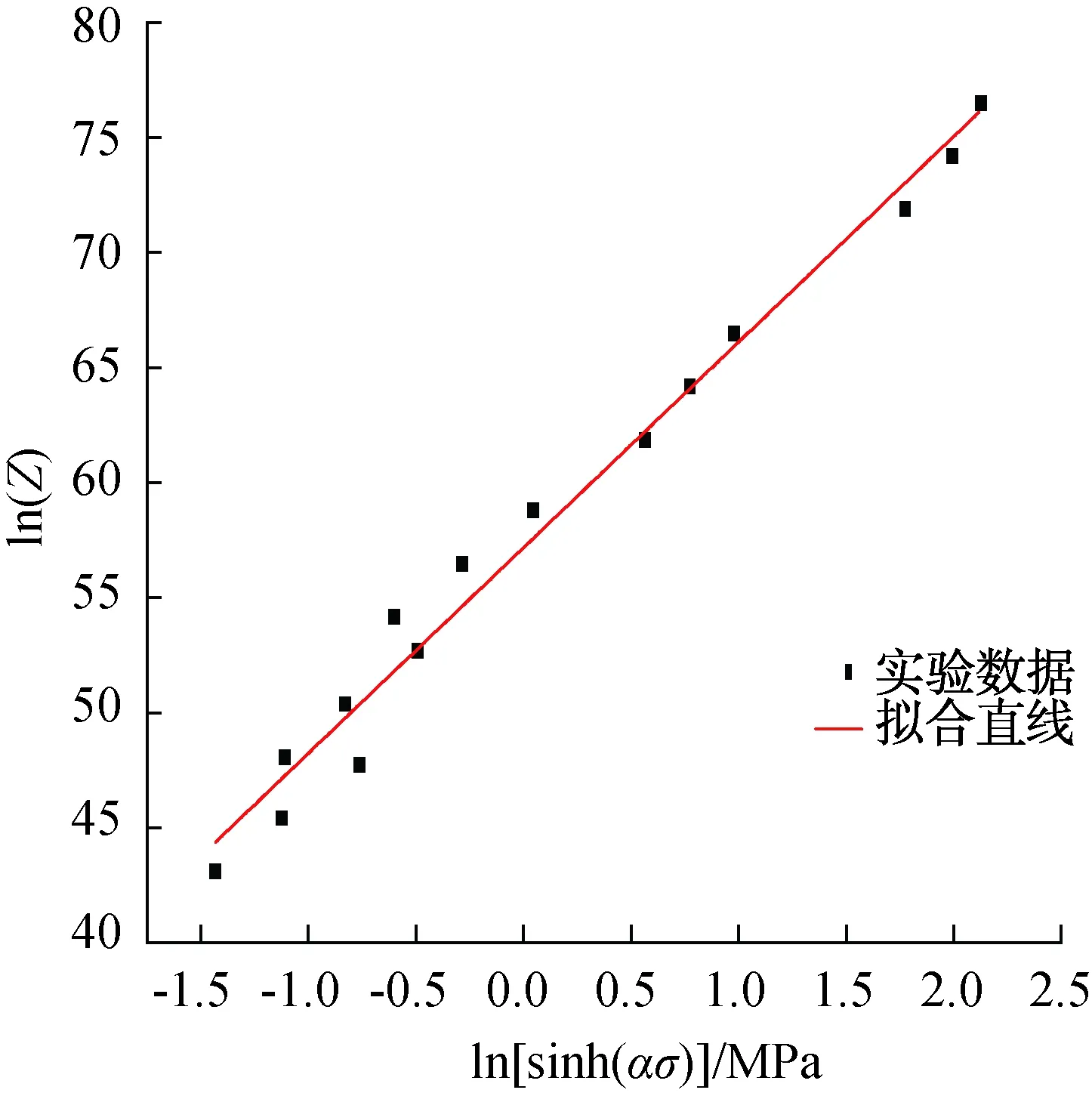
图4 Z参数与峰值应力关系Fig.4 Relationship between Z parameter and peak stress
2.2 自适应系数Arrhenius本构模型的求解
对于自适应系数Arrhenius本构模型的求解,实质上就是对每一点的真应力值使用2.1中的方法对材料常数进行求解.但原始数据具有大量噪点,取不同变形条件同一真应变条件下的真应力时也会出现缺值现象,因此本文采用3次样条插值法:首先,对每个变形条件下从0到0.9的真应变数据取6000个观察点进行插值;然后,对获得的6000个点求其对应的材料常数;最后,使用公式⑥进行多项式拟合.
图5为使用多项式对材料常数拟合后,拟合多项式最高项次数与决定系数R2的关系图.由图5可以看出,当多项式次数高于16后,拟合后的决定系数R2不再增长.因此,本文采用最高项次数为16次的多项式进行拟合,拟合结果如表1所示.将表1中的材料常数多项式系数代入公式⑥与⑤,即得自适应系数Arrhenius本构模型.

表1 材料常数多项式系数Table 1 Polynomial coefficient of material constant

图5 材料常数拟合多项式最高项 次数与决定系数关系Fig.5 Relationship between the highest degree of material constant fitting polynomial and the coefficient of determination
2.3 自适应系数Arrhenius本构模型的验证
图6为6063-T5铝合金在不同热变形条件下实验值与模拟值曲线图.由图6可以看出,虽然在变形温度为225 ℃且应变速率较低时,预测的真应力值与实验数据相比出现了一些偏差,但误差较小,对于实际数值模拟影响不大,这同时也说明自适应系数Arrhenius本构模型对于高温热变形行为的描述准确性更高.整体来看,模型计算出的数值分布在实验数据两侧,与实验数据偏差较小.综上可知,建立的自适应系数Arrhenius本构模型能够准确描述6063-T5铝合金的流变行为,可以用于数值模拟与热变形行为的分析.

图6 6063-T5铝合金在不同热变形条件下实验值与模拟值曲线图Fig.6 Curves of experimental values and calculated values of 6063-T5 aluminum alloy under different deformation conditions
3 6063-T5铝合金位错密度增长模型
3.1 位错密度增长模型的构建
对图2及相关研究[23,27]综合分析获得的热压缩真应力-真应变曲线示意图如图7所示,其中εc指发生再结晶时的真应变即临界应变,εp指真应力达到峰值时的峰值应变,σc与σp分别对应临界应力与峰值应力,σs指材料加工硬化和材料软化机制(只有动态回复)相互作用达到动态平衡后的饱和应力,σss指材料加工硬化和材料软化机制(动态回复与再结晶共同作用)相互作用达到动态平衡后的稳态应力.

图7 热压缩真应力-真应变曲线示意图Fig.7 Schematic diagram of true stress-true strain curve for hot compression

⑧
式中,k1指硬化系数,表示位错密度增长的趋势;k2指软化系数,表示位错密度减小的趋势.通过对公式⑧求解微分方程可以获得在恒温、恒应变速率下的位错密度公式⑨.
⑨
式中,ρ0是当真应变ε=0时的初始位错密度,则饱和位错密度ρs=(k1/k2)2.引入经典描述位错与应力关系的Taylor公式⑩[28],可将公式⑨转化为公式,即工作硬化应力模型.
⑩
式中,σ为真应力,μ为材料的剪切模量,b为伯格斯矢量.
式中,σ0为初始应力,σs为饱和应力.
3.2 位错密度增长模型的求解
对于位错密度增长模型的求解,即是对σs、σo、k2的求解.其中关于σs的求解本文选用文献[29] 提出的加工硬化率与应力曲线的拐点处作为临界应力,并进一步使用3次多项式拟合求解临界条件的方法进行求解.首先,对原始数据进行多项式拟合.对多项式进行求导后,真应变范围取[0,1],并以0.005为间隔取点,将所取观察点代入求导后的多项式中,获得加工硬化率(θ=dσ/dε)数据.考虑求导后θ的数据点形态,由于整体采取3次多项式拟合效果较差,所以采用移动窗口加权平均法中的Savitzky-Golay方法,以30个点为一个窗口进行3次多项式拟合,得到图8所示6063-T5铝合金在变形温度300 ℃时的加工硬化率拟合曲线.拟合曲线拐点处对应的真应力即为临界应力σc,由此点作延长线与θ=0的交点即为饱和应力σs.由真应力曲线可知,初始应力σo取原始曲线进行3次样条插值后的σ0.2%.
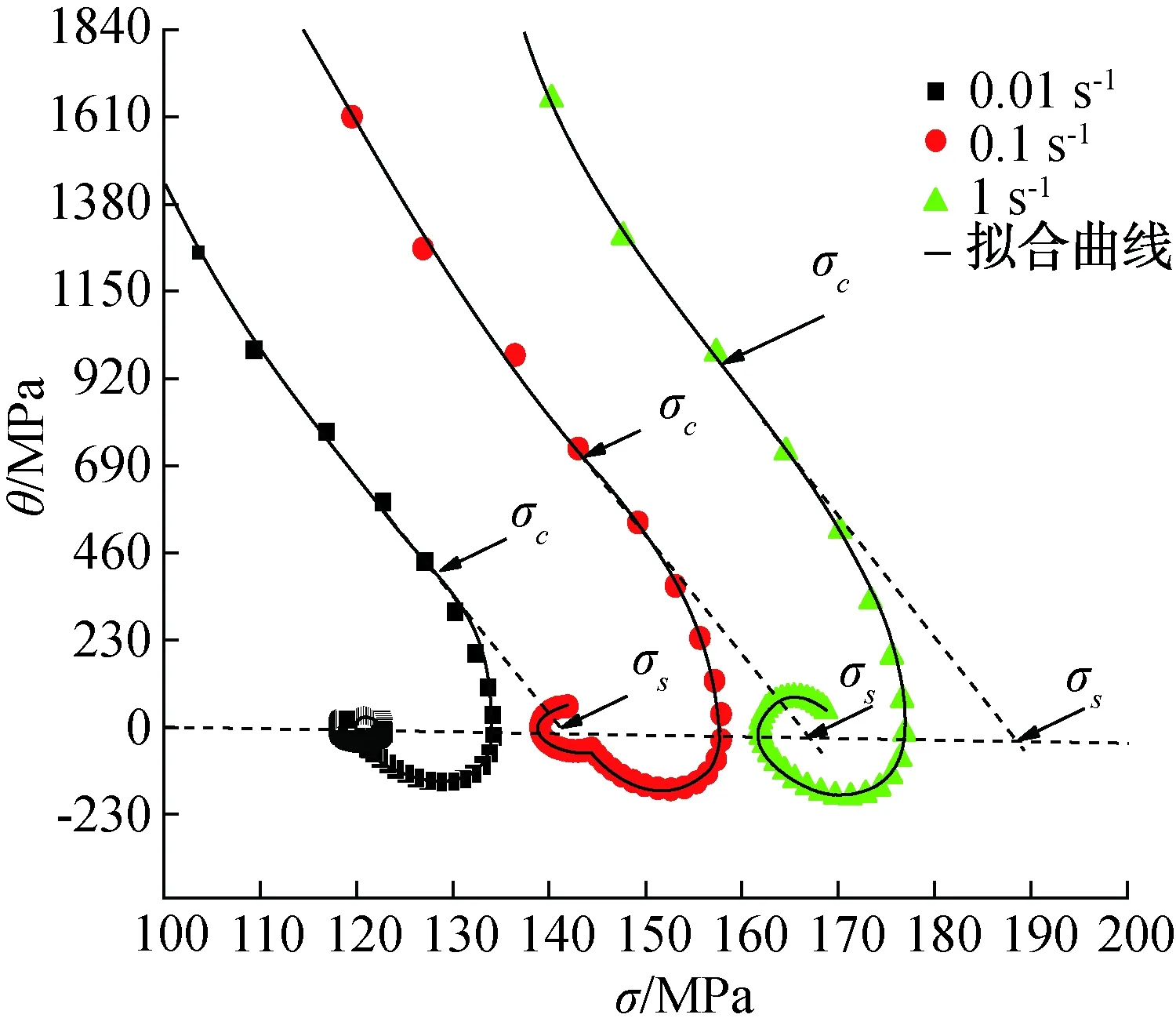
图8 6063-T5铝合金在变形温度300 ℃时的 加工硬化率拟合曲线Fig.8 Fitting curves of work-hardening rate of 6063-T5 aluminum alloy at a deformation temperature of 300 ℃
为了得到更普适的σs、σo与变形参数之间的关系,使用2.1中所得的材料常数建立如公式④的σs、σo变形参数关系模型,绘制lnsinh(ασs)-lnZ与lnsinh(ασo)-lnZ关系图并进行线性拟合,取斜率平均值获得对应饱和应力σs与初始应力σo模型,如公式与所示.
σs=100.19sinh-1(0.001 5Z0.115)
σo=100.19sinh-1(0.110 8Z0.073)
参照文献[19-20],选取εc为0.8εp.将公式、公式、真应力σ与真应变ε小于0.8εp的值代入公式中计算k2值,并建立其与Z参数的关系模型,如公式所示.绘制lnki-lnZ关系图并进行拟合,如图9所示.图9中lnk2-lnZ拟合曲线斜率即为n7,截距即为lnn6,对应求解可得k2,如公式所示.
k2=n6Zn7
k2=1.117×104Z-0.060 2

式中:μ由公式计算可得,b是柏氏矢量,为2.45×10-10m.

图9 lnki-lnZ关系图Fig.9 The relation chart between lnki and lnZ
k1=2.318×1011Z0.024 4
3.3 位错密度增长模型的验证
图10为实验数据与位错密度增长模型真应力-真应变趋势图.本文所建立的位错密度增长模型如公式⑧所示,是一种导数模型,其主要用来模拟6063-T5铝合金在热变形过程中位错密度的变化趋势.图10是使用Taylor关系把这种观察十分困难的位错密度趋势变化情况转为真应力的变化趋势.通过结合前文图7可知本文求解的位错密度增长模型,在真应变小于临界应变的开始阶段与实验结果一致,但当其大于临界应变后因位错密度模型不考虑软化机制的硬化模型,所以图10呈现出与图7相似的变化趋势.说明所建立的位错密度增长模型可以准确反映材料热变形过程中这种位错密度变化趋势.且由图10可以看出,在变形温度为225 ℃时,实验结果也无动态再结晶现象,而在300 ℃时,有再结晶发生,且软化程度与应变速率成反比,当应变速率较高时,软化效果较差.这主要是应变速率决定了再结晶形核与长大的时间,所以在低应变速率时软化效果更明显.因此,本文所建立的位错密度增长模型,可以用于数值模拟与热变形行为的分析.
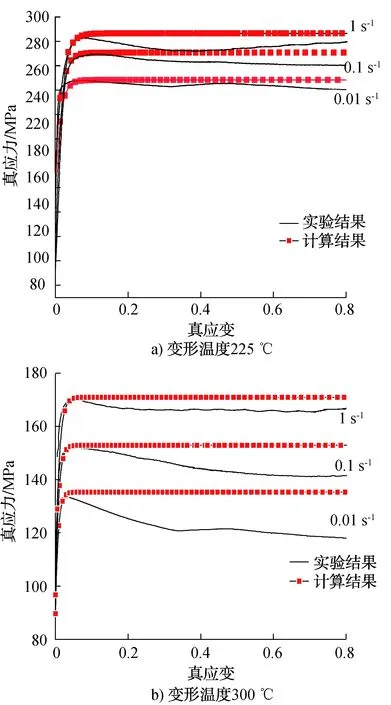
图10 实验数据与位错密度增长 模型真应力-真应变趋势图Fig.10 Experimental data and dislocation density growth model true stress-true strain trend diagram
4 6063-T5铝合金热加工图分析
热加工图是基于动态材料模型发展而来,用于描述金属热变形行为的主要模型.动态材料模型,主要是用来反映加工时材料在不同热变形条件下内部组织的变化情况,用于精准评估材料的加工性能,为金属材料的塑性加工制定最佳工艺参数[30].热变形过程中的能量P可由公式计算获得[31].
P=G+J
式中,G表示热变形过程消耗的能量,J表示微观组织演变消耗的能量.功率耗散因子η可使用应变速率敏感系数m获得,如公式所示.
图11为真应变分别为0.3,0.6,0.9时6063-T5铝合金的热加工图,其中等值线的值为功率耗散因子,黑色阴影部分由深到浅表示失稳因子的值偏离于0的程度.由图11可以看出,随着真应变值的增加,失稳区呈现向低温高真应变区域缩小的趋势.随着温度的升高,功率耗散因子逐渐增加,且高功耗因子集中在中高温区域,当真应变值达到0.6后耗散因子等值线变化不明显.
以真应变值为0.9的热加工图(即图11c))为例进行分析,6063-T5铝合金在该变形条件下,流变失稳区主要集中在低温高真应变区域,这是由于在该区域6063-T5铝合金容易应力集中,产生塑性成形缺陷,在实际热变形中应避免在该区域进行热加工.而在高温区域功率耗散效率值高,且不处于流变失稳区.因此,适合6063-T5铝合金的热加工工艺参数为变形温度350~525 ℃、应变速率0.01~1 s-1.

图11 不同真应变6063-T5铝合金的热加工图Fig.11 The hot processing map of 6063-T5 aluminum alloy under different true strains
5 结论
本文通过热模拟实验,研究了6063-T5铝合金的热变形行为,分析发现:随着温度的升高,材料的软化效果越来越明显,且随着应变速率的提升,材料的硬化效果越来越明显.建立了自适应系数Arrhenius本构模型与位错密度增长模型.验证实验结果表明:两模型可以描述热变形参数对6063-T5铝合金热变形行为的影响,且自适应系数Arrhenius本构模型对于中高温热变形行为的模拟更加精确.利用实验所得真应力-真应变曲线建立了ε=0.3、ε=0.6、ε=0.9的6063-T5铝合金热加工图,并以ε=0.9为例获得了其最佳变形温度350~525 ℃、应变速率0.01~1 s-1.本文的研究结果可为6063-T5铝合金的热变形行为及位错密度微观分析提供可适用性模型,为6063-T5铝合金的热变形行为的理论研究与热加工参数的选取提供依据.
