优化RBF神经网络控制水厂混凝剂投加的研究
2021-09-02庹婧艺徐冰峰王雪颖郭露遥
庹婧艺,徐冰峰,徐 悦,喻 岚,王雪颖,郭露遥
(昆明理工大学建筑工程学院,昆明650000)
混凝投药是自来水厂运行的关键,投加量直接决定着水厂的出水水质和经济效应。在保证出厂水水质达标的情况下,实现投药量的最佳控制,是净水行业现阶段的重点[1]。张瑶瑶、刘泽华[2,3]研究发现因原水浊度对投药量的影响大,采用回归方程模型分析水厂投药量时,须将样本分为高浊与低浊两个方程分别计算,其计算方式冗杂,对数据要求高。李培军、唐德翠[4,5]等人采用机理模型模拟投药工艺,模型只是在一定的特殊条件下建立的,需要对自来水厂投药混凝的各影响因子都进行解析计算,其准确度不是很高。王晓杰、李拓[6,7]等人采用BP神经网络预测混凝投药量,网络本身收敛速度慢,网络规模小,精度难以提高。研究结果如表1。
据表1可知,由于单一神经网络结构自身所具有的约束性,还需其他组合算法来增加模型的全局搜索能力[9]、降低运动过程的鲁棒性、提高预测精度[10,11],从而达到模型目标期望值的目的。本文采用PSO 优化RBF 建立非线性的高维映射水厂投药量动态模型,以了解原水数据与投药量之间的规律,实现在不同季节、不同水厂、不同条件下对投药量的动态预测,尽早发现水质变化趋势,降低药耗。
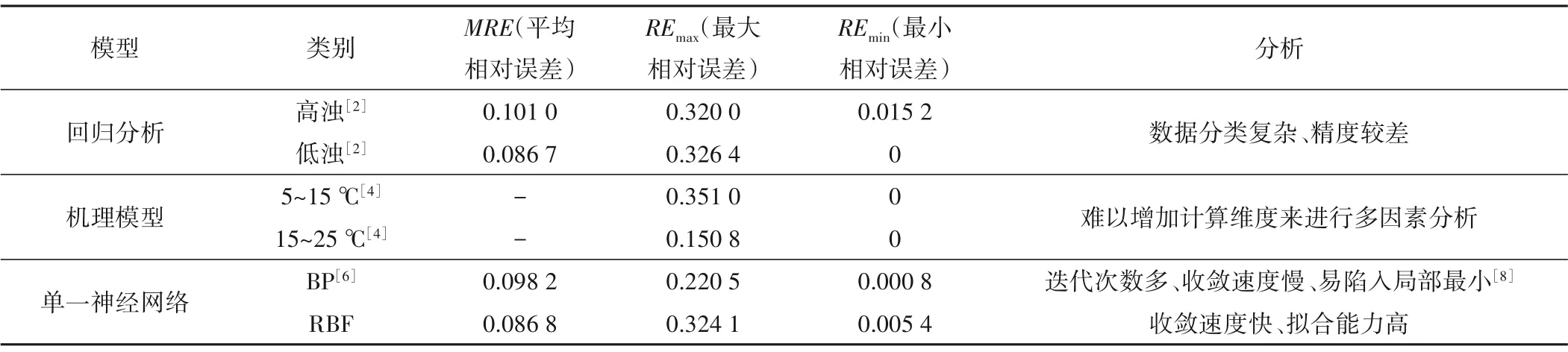
表1 自来水厂常用模拟算法精度对比
1 PSO优化RBF神经网络模型的建立
1.1 RBF神经网络结构
RBF 能将训练样本点使用核函数方法(Cover 函数)投射到更高维的空间中,可以近似任意非线性函数,精度较高,能避免陷入局部最优[12,13]。
影响混凝沉淀的因素很多,根据水厂实地调研以及前人研究表明,原水指标中影响投药量的主要因素有Q(原水流量)、NTU(浊度)、原水pH、CODMn(耗氧量)、温度、电导率、藻类等[14,15]。考虑上述影响因素对混凝投药的敏感度,本文选取Q、NTU、pH、CODMn四个指标作为输入值的维度,投药量作为输出值的维度[16],建立网络结构(如图1)。
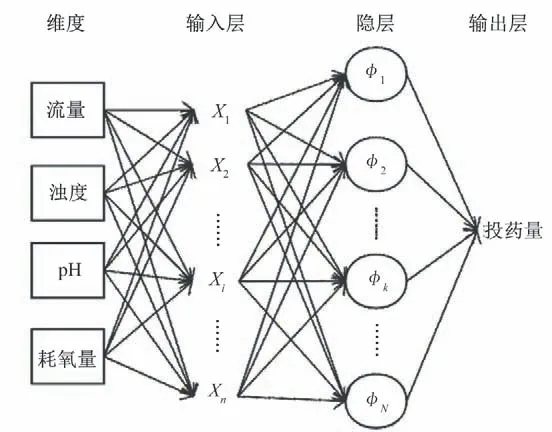
图1 RBF神经网络模拟水厂投药量结构
设输入值为Xk,那么投药量输出值Y(x)为式(1)。
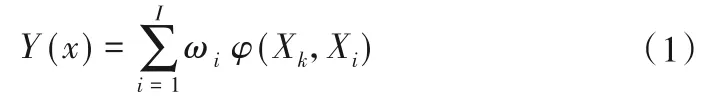
式中:Xi为基函数的中心;ωi为输出单元与中心的连接权值;φ(Xk,Xi)为基函数。
1.2 PSO优化RBF网络的程序
本文采用PSO 优化RBF 算法,建立水厂投药量模型(如图2)。
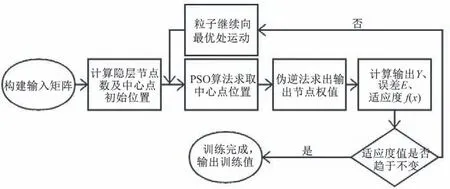
图2 创建RBF优化组合模型流程图
PSO 算法中每一个粒子的位置和速度都由适应值f(x)衡量优劣。本文将减法聚类算法所得到的中心点作为初始中心点位置,用PSO 算法优化更新RBF 网络中心点位置。粒子的路径与速度[17]由式(2)、(3)决定
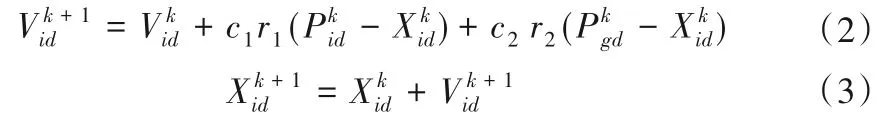
式中:为粒子i在D维空间中第k次游走的运行速度;为粒子i在D维空间中第k次游走后的位置;为粒子i在D维空间k次运动后的个体最佳位置为粒子在D维空间第k次运动后,粒子群体的全局最佳位置;c1、c2为加速常数,取值一般在1.5~2.0之间时,算法效果较好;r1和r2为[0,1]内的随机数。
取RBF函数E(均方误差)的倒数作为PSO算法的适应度函数f(x)。采用误差倒数E作为函数的适应值,能约束粒子群体运动轨迹,从而通过误差反向传递动态地调节RBF 神经网络的输出值。
(1)减法聚类法确定节点数N。基函数中心点个数即隐藏节点数由减法聚类算法得到[18]。数据X(x1n,x2n,x3n,x4n)归一到单位的D维空间后,按照式(4)计算每个训练样本i处的密度指标。
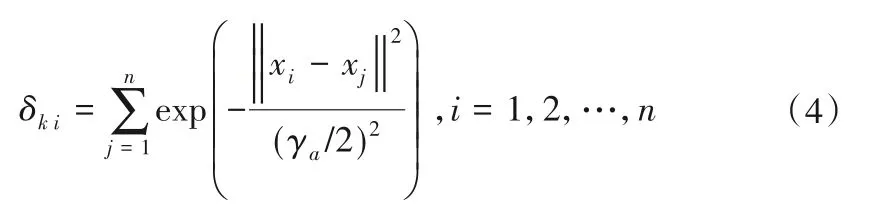
选取初次计算地密度指标最大处δ0=max(δki)的训练样本点,作为减法聚类的第一个聚类中心,xj为随机初次聚类中心点。
根据式(5),将第k次计算的密度指标δkmax的训练样本点xkmax作为中心,更新k+1次样本数据的最大值密度指数。
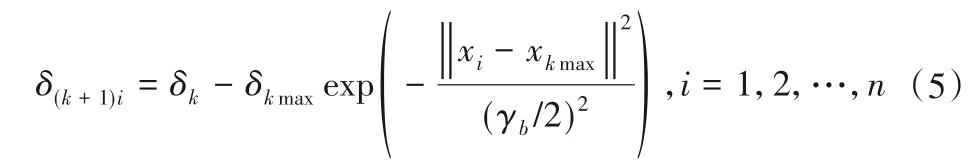
式中:γa,γb由公式(6)确定。
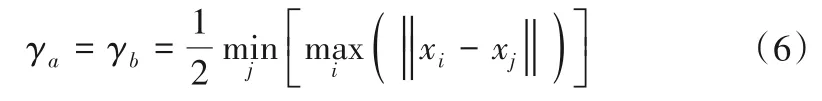
由式(5)得出第k+1次计算的密度指数δk+1,当时,循环结束。所得到的聚类中心个数即为RBF 网络基函数中心个数N。式中σ为聚类中心点的邻域半径,是约束各个粒子属于哪类聚类中心的分类归属,一般σ≥0.5[19]。
(2)基函数计算标准差σ。广义RBF 网络的基函数一般采用高斯函数[19],高斯函数标准差σ由式(7)确定:

式中:dmax是所选取的各个聚类中心点之间的最大距离。当函数有多维度时,以两点之间的范数代替;N为RBF 网络隐层节点个数。
(3)PSO 算法更新RBF 网络中心点位置。将减法聚类算法所得到的中心点作为初始中心点位置,据式(3)式计算粒子每次运动位置。据式(1)求得的输出值Y,计算得适应度函数为式(8):
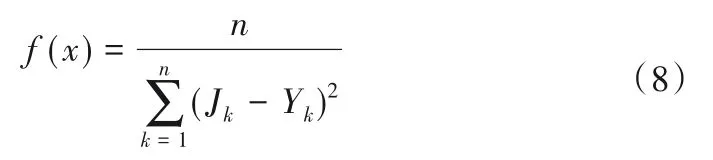
式中:Jk为第k次的实测值;Yk为第k次的预测输出值。
以式(8)来约束式(3)的运动过程,最终求得每个中心点的位置,得到中心点Xpop(x1N,x2N,x3N,x4N)为N的矩阵。
(4)伪逆法确定RBF 函数权值。J=J(xn)为期望输出,假设Jij为第i个输入向量在第j个输出节点的期望输出值,ωkj为第k个隐层节点到第j个输出节点的权值,i∈(1,n),j∈(1,n),k∈(1,N)。则权值矩阵ω可用式(9)求得:

式中:G={gik};矩阵ω=ωkj。
(G)+伪逆矩阵,可由式(10)作奇异值分解(SVD)求取。

式中:gik是第i个输入向量在第k个隐层节点处的输出值;Xi为第i个输入向量,Xk为第k个隐层节点输入向量。
将求解得的函数模型中心点位置Xid、标准差σ、隐层节点个数N、函数权值ω参数代入式(2)即可得出优化模拟后的函数式。将训练数据输入初始优化函数,得出的输出值与实际值进行对比,由PSO的适应度f(x),动态地约束调节基函数中心点位置,最终得到误差最小的拟合参数,得出投药量输出矩阵Y=Y(Yn)。
2 案例分析
2.1 数据选取
选取昆明某自来水厂[水库水,8 万m³/d,混凝剂PAC(聚合氯化铝)],2018年1月-2020年7月的211 组监测数据进行随机排列,确定90%(191 组)的数据作为训练样本,10%(30 组)的数据作为测试样本[20]。摘取训练样本数据创建4×191 的输入矩阵,X(x1n,x2n,x3n,x4n),n=1,2,…,191,创建1×191 的矩阵作为实际输出值J矩阵,J=J(xn),n=1,2,…,191。
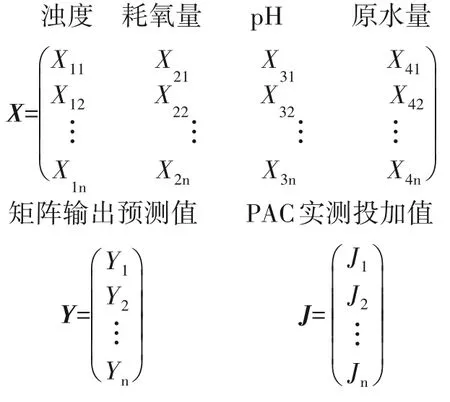
采用荆州某水厂(水库水,3 500 m³/d,混凝剂PAC),2020年6-12月50 组原水水质监测数据的60%(30 组)作为训练样本,40%(20 组)作为测试样本,对已建立的优化模型进行自适应性检验。
2.2 结果分析
2.2.1 运行结果
经计算,昆明某水厂的模型中网络中心点个数N为13,迭代70 次收敛,RBF 函数的输出权值为ωmax=53.25、ωmin=-63.30,邻域半径σ=0.58,粒子群加速常数C1=C2=1.578,将最优拟合参数代入式(2)得出优化模拟后的函数式,计算出混凝剂投加的模拟值与实际值MRE为0.056 3。荆州某水厂网络中心点个数N变为11,迭代次数在20 次就发生收敛,计算得到MRE0.043 1,MAE(平均绝对误差)0.195 4,REmax0.171 8。如图3所示,PSO 优化RBF 网络模型对两个不同的水厂,预测运行结果表现力优秀,平均相对误差都在6%以下,模拟精度较高。

图3 不同水厂预测数据与实测数据运行结果对比
2.2.2 优化模型性能分析
如图4所示,以昆明某水厂为例,单一RBF神经网络代次数在200 次左右才达到收敛,而PSO 优化后的RBF 神经网络70 次就能收敛。迭代次数明显降低,算法模型运行速率更快。
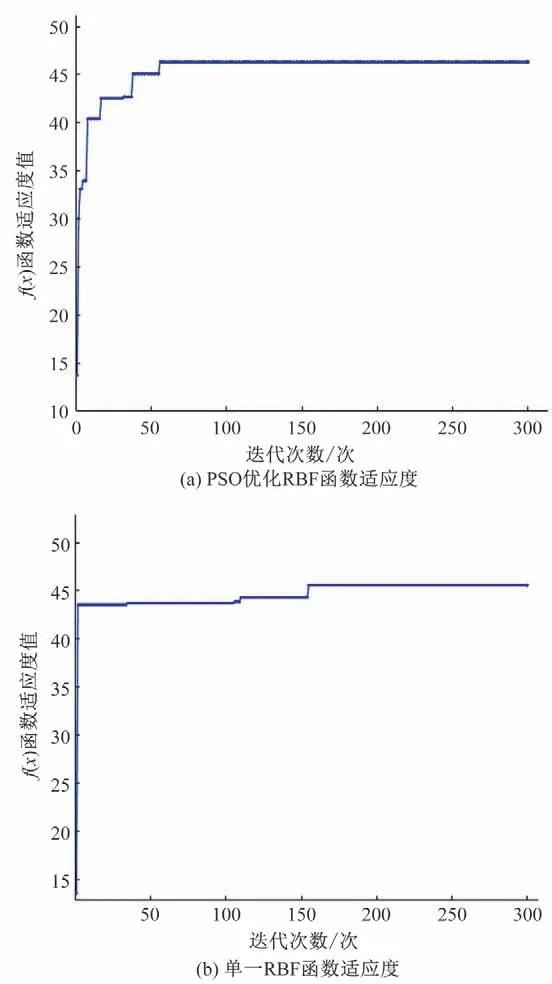
图4 迭代次数对比
由图5可知,单一RBF神经网络预测的总体误差较大,且存在较大波动,对实际拟合能力差。而PSO 优化RBF 组合神经网络模型精度明显提高,它具有更好的数据拟合能力和模型的稳健性。
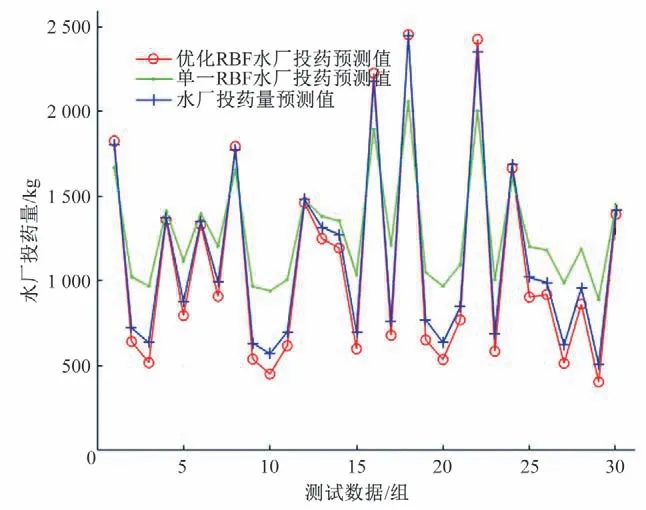
图5 优化后的函数与单一函数运行结果对比
以昆明某水厂为例,由表2比较分析,PSO 优化RBF 神经网络相较于单一RBF 神经网络,对于水厂混凝投药量预测平均相对误差降低了3.05%,最大相对误差降低了0.198 6,模拟精度更高,能很好地预测水厂投药量。
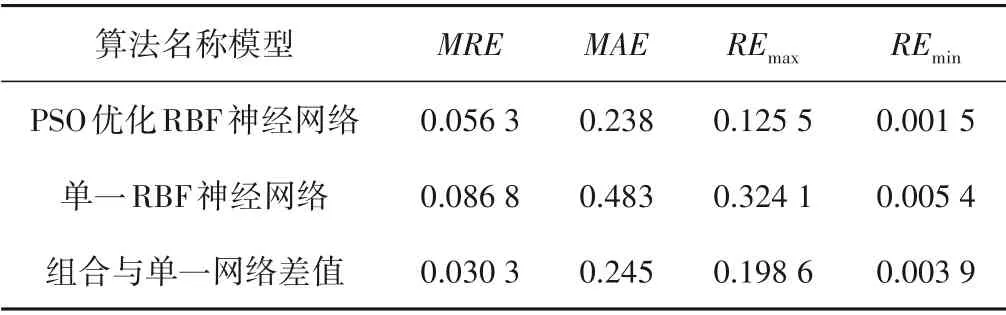
表2 优化组合的RBF与单一RBF模型运行精度对比
3 结论分析
(1)高浊度期和低浊度期数据对PSO 优化RBF 神经网络输出影响不大,训练参数时间顺序可不作为模型的约束条件,模型预测结果比回归方程求解输出更为精准。
(2)PSO 优化RBF 神经网络模型减少了对水厂每个单元的机理模拟,可直接通过模型得出投药与原水水质的映射关系,可适用于不同地理位置的水厂。
(3)粒子间的合作与竞争使模型增加对多维复杂空间的高维搜索能力,快速得出神经网络权值的最优解,故优化RBF 模型比单一RBF 网络具有更高的精度,其鲁棒性降低,收敛速度更快,可为模拟自来水厂投药量提供有效参考。□
