基于HS算法优化的EEMD-RNN混凝土坝位移预测模型

2021-09-02范鹏飞祝福源

中国农村水利水电 2021年8期

范鹏飞，祝福源

（1.山西省水利水电工程建设监理有限公司，太原030000；2.河海大学水利水电学院，南京210098；3.水发规划设计有限公司，济南250100）

0 引言

混凝土坝作为一种重要的坝型，在服务经济发展方面起着重要作用。随着现代监测技术的发展，混凝土坝的监测越来越系统化、智能化，监测的数据库也越来越庞大，对于数据的科学分析特别是高坝和特高坝的处理尤为重要。混凝土坝监控系统的监测项目一般包括位移、应力应变、渗流渗压、裂缝发展、坝体温度、钢筋应力应变、环境量等。其中由于混凝土坝相较于其他材料大坝具有较高的刚体结构特性，使得位移成为混凝土坝安全运行管理研究的首要指标［1］。研究学者们已经对其进行了较为全面的研究，如位移的拟合和预测、影响位移的因素、基于位移的坝体材料参数反演、大坝位移预警指标的拟定等［2-4］。而位移预测和预判对大坝安全管理决策的作用愈加凸显，并且对位移预测的精度和模型的适用性和可靠性的要求越来越高。因此预测混凝土坝的位移进行和提高预测精度对大坝安全就十分必要。

在大坝位移的预测方面，传统的方法有统计学，如多元回归法、逐步回归法［1］；模糊数学预测模型及确定性预测模型等［5］。近年来随着计算机技术及软件的发展，智能算法在大坝位移预测领域应用也越来越广泛。由单一算法向串联算法发展，而组合智能算法利用各算法的优点并且较好地克服了单一算法的过拟合问题，提高了模型的非线性映射能力、计算效率和预测精度，如徐朗等采用改进的PSO-SVM 模型研究了大坝的变形［6］；郭志扬等构建了卡尔曼滤波的GA-BP 大坝变形预测模型［7］；何启等应用PSO_GM_MC 灰色神经网络-加权马尔可夫链组合算法组建了大坝变形监控模型［8］。而在研究混凝土坝位移预测的问题上，由于混凝土坝位移受非线性变化的水位、温度、时效等因素影响，再加上监测噪声误差的存在，使得位移信号的非平稳性比较明显，无疑增大了对位移的拟合和预测的难度。为解决信号的非平稳性的难题，Huang［9］于1998年提出了经验模态分解（empirical mode decomposition，EMD）方法，但该算法的信号包络易发生形状畸变并引起端点效应，从而使各个分量的分解不准确。Wu.Z等［10］在EMD 算法的基础上提出了集合经验模态分解（ensemble empirical mode decomposition，EEMD）可以有效地解决上述EMD 算法的缺点。EEMD 算法应用已较为广泛，如刘淑琼等利用EEMD-RBF神经网络构建了电离层TEC 预报模型［11］；李华等通过EEMD 算法实现了轴承故障特征的提取［12］；谭冬梅等基于EEMD-JADE 较好地分离出桥梁挠度监测中的温度效应［13］。为了提高训练拟合及预测精度，引入递归神经网络（Recurrent Neural Networks，RNN）算法。RNN神经网络是一种结构优化的神经网络，在隐含层中引入了循环结构并且在隐含元单元之间进行内部联系，在训练过程中信息可以在模型中向前或者向后传播，这可以提高算法的训练效率和精度。目前，应用该算法的研究成果颇多，如周暄焯通过RNN 及其融合方法研究预测了DNA 甲基化的状况［14］；芦效峰等构建了CNN 和RNN 组合算法以探索自由文本击键模式持续身份的认证［15］；范竣翔等基于RNN算法研究了空气污染时空预报模型［16］。而大坝位移在监测过程中，监测值中包含了测量误差和系统噪声，为了进一步提高训练拟合的精度和算法的健壮性，本文采用和声搜索算法（harmony search algorithm，HS）进行去噪优化，可以有效地提高预测精度，如张磊等利用和声搜索算法可以较好地提取近红外光谱特征变量［17］；李明等基于和声搜索算法实现了无线传感器网络多重连通覆盖［18］；王志刚等通过和声搜索算法优化了RGV动态调度模型［19］。

综上可知，单一算法模型在解决复杂的问题时比较困难，而对于受复杂条件影响的大坝位移具有随机性和非线性，实现较高精度的预测则更加困难。因此，为克服单一算法容易陷入误差函数的局部极小值、收敛速度慢、过度收敛等缺点，本文首先利用EEMD 算法进行位移监测数据的平稳化处理，然后利用RNN 神经网络较强的非线性映射能力，通过训练样本集学习建立混凝土坝环境量、时效和大坝位移的非线性关系，采用和声搜索算法对其去噪和优化，综合各算法的优势，提高位移预测精度和模型计算效率，构建HS-EEMD-RNN 混凝土坝位移预测模型。

1 模型基本理论

1.1 集合经验模态分解（EEMD）

EEMD算法通过在原始时间序列中加入足够多的正态分布白噪声，再将新的时间序列进行EMD 分解；然后利用白噪声均值为零的特性对各分解量作算术平均，可得到EEMD 分解的IMF分量和剩余项R。分解步骤如下［13］：

（1）首先把等长度高斯白噪声N次加入原始时间序列，则可得到若干新的时间序列：

式中：yi(t)为第i次加白噪声后的时间序列；y(t)为原时间序列；ni(t)为正态分布白噪声信号。

（2）然后通过EMD 算法分解添加白噪声的新时间序列，可得到本征模态函数wi j(t)及一个剩余项ri(t)：

式中：wi j(t)为第i次添加白噪声后分解所得到的第j个本征模态函数分量；ri(t)为剩余项。。

（3）再将N组本征分量及剩余项r(t)求平均得到最终的IMF分量及剩余量R(t)。

式中：IMFj(t)为EEMD最终分解分量；R(t)为最终剩余量。

（4）最后，原始时间序列信号可分解为：

1.2 递归神经网络（RNN）

RNN 神经网络的优点在于一次性激活不同的神经单元，即当前时刻的隐含层节点能够反应前一时刻隐含层节点的输出内容，同时作为输出层的输入以及前一个时间点的隐含层的节点输入，并在处理该时刻的信息之后又导向下一时间点的隐含层节点［14］。RNN 较之传统的神经网络，在训练拟合和预测位移的过程中，可以提高收敛速度和训练精度，其在时间维度上展开后结构如图1。

图1 RNN在时间维度上展开的结构Fig.1 The structure of RNN in time dimension

由图1可知，RNN 在时间维度是一个不断往后递归的过程，之前时刻的结果对下一个时刻的训练有着直接的影响，但因为在每个时间步上的权值一样，所以在相同时刻不同单元会共享同一组权值。对于长度为T的序列x，RNN 的输入层大小为I，隐含层大小为H，输出层大小为K，可得3 个权重矩阵U、V和W的维度［15］：

定义xt为序列中第t项输入；at为第t项隐含层的输入；bt为对at进行非线性激活，即神经网络的输出。因此，at是由输入层xt与上一层隐含层的输出bt-1共同决定：

大坝位移监测序列由t=1 开始，所以b0= 0，然后把隐含层的信息传导输出层，则输出层的输出结果：

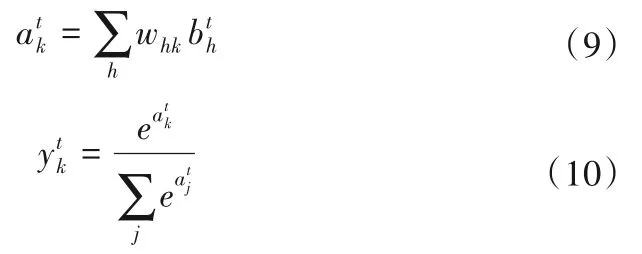
在t时刻，普通神经网络的残差为δtk=ytk-ztk，而RNN 由于前向传导时隐含层需要接受上一个时刻隐含层的信号，而且在反向传导时还需要接受下一个时刻隐含层的反馈，则RNN输出层的残差项：

当位移序列长度为T时，则残差δT+1均为0，同时整个网络只有一套参数U、V、W，则时刻t的倒数：

则可以写成统一的形式（假定对输入层有xti=ati=bti）：

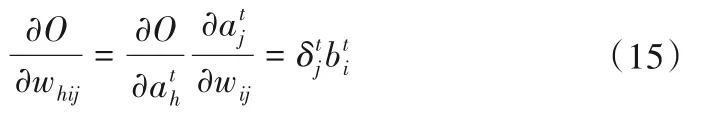
最终，对时刻t=1，2，…，T，由RNN神经网络的递归性，将其求和可得RNN网络关于权重参数的导数：

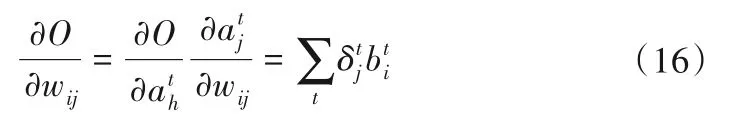
1.3 和声搜索算法

对于EEMD 分解得到的位移分量，其中高频分量主要由监测误差噪声引起的，尤其是IMF1 分量，所以对其系统性去噪以提高模型的精度就很有必要。和声搜索算法的基本思想是模仿乐队演奏的和声调谐过程的元启发式优化算法［20］，其优化RNN神经网络的实现过程如下［21］：

步骤一：初始化相关算法参数。

和声搜索算法参数有：和声记忆库容量HMS、和声记忆库取值概率HMCR、微调扰动概率PAR、微调步长bw、迭代次数BT。HMS决定了HS 算法的全局搜索能力，但过大的HMS值会影响收敛到最优解的速度，HMCR值大有利于算法的局部搜索，算法参数的具体数值可由仿真试验确定［22］。

步骤二：定义目标函数并初始化和声记忆库。

定义目标函数：期望输出（实测值）与网络输出（拟合值）的平均相对误差F，其中F值越小表明优化程度越好。

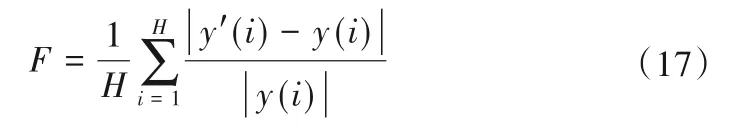
式中：H为训练集样本总数；y'(i)、y(i)分别为第i个样本的实测值与拟合值。

构造HMS个随机初始和声x1、x2、…、xHMS添加和声记忆库，记忆库中的和声xi对应RNN 神经网络的一组权值和阈值。和声记忆库为：

式中：xij为RNN 网络中第i组和声的第j个权值或阈值；（fxi）为第i组目标函数值，即第i组网络输出与期望输出之间的平均相对误差。

步骤三：新和声的创作。

创作新和声，即构造新的解向量。根据学习和声记忆库、音调微调，随机产生新和声的音调x'j（j=1，2，…，N）：

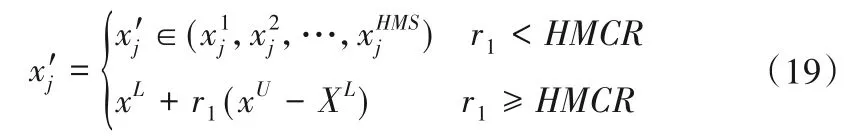
式中：r1为［0，1］内均匀分布的随机数；为在第j列HMS个分量中随机选定的分量；xU、XL为第j列分量的取值上下限；式（19）为对任意新音调x'j，会以HMCR的概率从记忆库中选取，以1-HMCR 概率从其对应的取值区间内随机取值［23］。如果x'j是和声记忆库中的解分量，则对其微调为：

式中：r2、r3分别为［0，1］和［-1，1］内均匀分布的随机数。

步骤四：更新记忆库。

如果新和声解向量对应的目标函数值F优于记忆库内的最差解，则用新的和声解替换最差解，更新记忆库。

步骤五：结束循环。

循环步骤三、四，直至满足终止准则或达到最大迭代次数。

2 构建模型及精度评价

2.1 组合模型建模步骤

综合以上算法的优点，基于HS 优化的EEMD-RNN 组合模型的详细步骤如图2，建模具体流程如下：

图2 基于HS优化的EEMD-RNN组合模型混凝土大坝预测流程图Fig.2 Flow chart of concrete dam prediction based on HS optimized EEMD-RNN combined model

（1）确定大坝位移的研究测点，通过EEMD 对测值进行分解，得到若干组IMF分量和剩余项R。

（2）应用RNN 神经网络算法对IMF分量和剩余项R进行训练拟合，输入为环境量和时效变量，输出为大坝位移。在训练过程中通过和声搜索算法HS 优化RNN 的阈值和权值，直到得到最优解。

（3）通过训练最优的拟合映射关系，计算预测集所对应的IMF分量和剩余项R。

（4）将各个分量位移IMF和剩余项R的预测值等权求和即为最终的预测结果。

2.2 模型精度评定

为了评价模型拟合及预测的精度，利用平均绝对误差（MAE）、均方根误差（RMSE）和平均绝对百分比误差（MAPE）进行模型的精度评定，分别为：

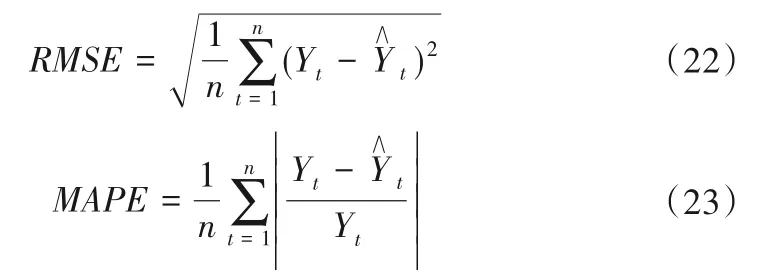
式中：Yt为混凝土坝位移实测值；为模型计算量；n为监测数据总个数；t为监测数据对应的时间。

3 实例计算

某重力坝位于中国东南省份，坝顶高程634.40 m，最大坝高72.4 m，坝体上游面垂直。大坝共分为9 个坝段，坝顶长206 m，坝顶宽7.5 m，其中4号和5号坝段是溢流坝段，其余为非溢流坝段。非溢流坝段下游面坝坡比为1∶0.72。其中该坝采用引张线监测坝体的水平位移，共布置1 条，固定端布置在坝右01+107.025 处，导向端布置在坝左0+93.50 处，全长200.75 m，每个坝段布置一个测点，共9 个测点，测点名称EX1～EX9，测点布置图如图3。

由图3可知，该坝引张线系统的EX5 测点位于大坝的中间坝段，监测大坝的顺河向水平位移，其位移变化具有典型性，所以选取测点EX5 为算例研究对象，且EX5 测点可靠，监测频次为1 次/d，采用自动化监测和人工校测，监测数据连续可靠。

图3 引张线测点布置图Fig.3 Layout of measuring points of tension line

通过基于HS 优化的EEMD-RNN 混凝土坝位移预测模型对该坝EX5 测点所监测的位移进行计算分析。位移监测资料选取2016年6月2日-2017年8月20日，共445 组，其中2016年6月2日-2017年6月30日的前395 组作为模型训练组，2017年7月1日-2017年8月20日后50组为模型预测组。

EEMD 分解参数有两个，高斯白噪声标准差Nstd一般为0.01～0.4，添加噪声次数NE一般为50 或100，为尽可能得到较好的分解结果，综合Nstd取0.01，NE取100。模型的训练集EEMD分解结果如图4，其中7组IMF分量及1组剩余量R，IMF1分量、IMF2 分量和IMF3 分量为高频分量，其余IMF分量为低频。对于高频分量，主要由监测误差噪声引起的，尤其是IMF1分量。所以系统性地去噪以提高模型精度就很必要。

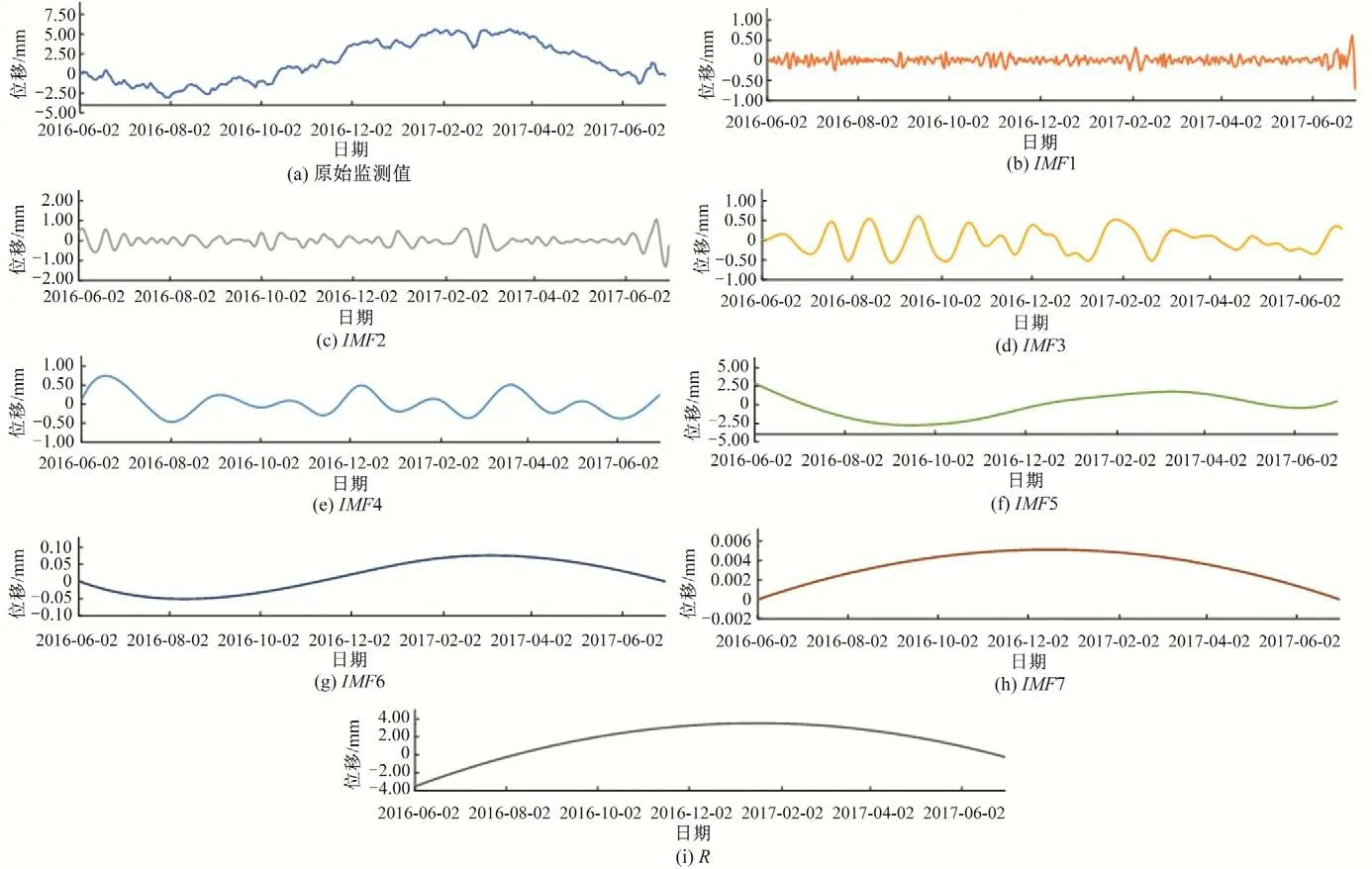
图4 大坝EX5测点位移EEMD分解结果Fig.4 EEMD decomposition results of displacement of EX5 measuring point of dam

为了降低测值中的噪声误差对训练结果的干扰，通过和声搜索算法优化RNN 训练过程，其中和声记忆库大小HMS取100，搜索范围为［-1，1］，和声记忆库保留概率HMCR取0.85，音调微调概率PAR取0.2，微调步长bw取0.2，最大迭代次数NT取100。在HS 优化RNN 训练结束后，对各分量IMF和剩余量R的拟合值进行等权求和得到位移的拟合值，拟合结果如图5所示。并且与EEMD-RNN 模型的拟合结果进行对比，拟合的精度见表1所示。由图5和表1可知，HS 算法可以有效提高训练拟合精度，HS-EEMD-RNN 模型的拟合精度明显高于EEMD-RNN模型。

表1 两种模型的拟合精度对比Tab.1 Comparison of fitting accuracy of two models

图5 两种模型的拟合结果Fig.5 Fitting results of the two models

由HS-EEMD-RNN 训练好的网络进行各个分量位移IMF和剩余项R的预测值，等权求和即为最终的大坝位移预测结果。同时计算了EEMD-RNN 的位移预测值，位移预测结果如图6。利用均方根误差（MAE）、平均绝对百分比误差（RMSE）、相对误差和绝对误差（MAPE），3 种指标对两种模型的预测情况评价，具体对比结果如表2。由图6和表2的对比结果表明，HSEEMD-RNN 模型的预测精度要优于EEMD-RNN 模型；而且预测精度高，能够满足工程要求。

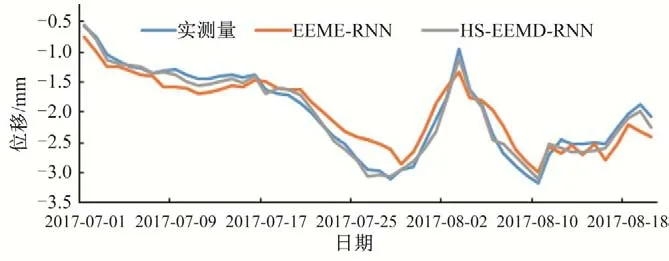
图6 EEMD-RNN模型和HS-EEMD-RNN模型对总位移的预测Fig.6 Prediction of total displacement by EEMD-RNN model and HS-EEMD-RNN model

表2 EEMD-RNN和HS-EEMD-RNN模型预测值误差对比Tab.2 Comparison of prediction error between EEMD-RNN model and HS-EEMD-RNN model

其中位移变化过程中的突跳点一般是大坝安全监控工作关注的重点，而以往模型的过拟合及预测误差大的情况在突跳点位置发生的较多，所以选取EX5 位移过程线突跳程度最大的10个测值与模型的预测值进行对比，以更好地评估模型的预测精度，位移突跳点预测值对比结果如表3。由表3可知，HSEEMD-RNN 的平均绝对百分比误差为4.93%，比EEMD-RNN的14.89%明显小得多。