堰-底孔组合式鱼道堰顶布置优化研究

黄建宇，魏 萍，纪 超，王 彪，王 浩

（1.南昌龙行港口集团有限公司，南昌330029；2.水利部交通运输部国家能源局南京水利科学研究院，南京210034；3.江西省港航建设投资集团有限公司新干航电枢纽分公司，江西吉安331300；4.江西交远物流有限公司，江西南昌330029）

0 引 言

隔板式鱼道按隔板上过鱼孔的形状，可分为溢流堰式、孔口淹没式、竖缝式及组合式。组合式鱼道可将各种型式鱼道的优点集合，取长补短，充分发挥各种型式鱼道的优势，适合多种鱼类同时通过，提高过鱼效率。溢流堰和底孔结合的堰-底孔组合式鱼道，不仅能较好地发挥两种类型过鱼孔的水力特性，灵活地控制池室的流速和水流结构，而且能满足不同习性鱼类的过鱼需求，是国外常用的鱼道型式［1，2］。其中，淹没孔口式鱼道适用于底层洄游的鱼类，能适应上下游较大的水位变幅［1，3］，溢流堰式鱼道适用于表层洄游和有跳跃习性的鱼类［4］。堰顶缺口将水流限制在缺口中，增加了池室中的能量耗散，溢流堰缺口型式有很多，有的布置在中央位置，有的布置在堰顶两侧左右交错，但通过大量的鱼类观测发现，一些鱼在穿过一系列有交错孔或交错槽的鱼道隔板时，表现得非常不适应，有交错孔或交错槽的鱼道池室内水流主流弯曲程度大，鱼类洄游道路曲折，不利于鱼类沿着主流上溯［5］。汪洪波［6］等运用数值模拟的方法研究了横隔板鱼道的水力特性，表明此类型鱼道内水流流态稳定。刘鹄［7］、王琲［2］、黄明海［8］等分别研究了竖缝式鱼道与孔口式鱼道、溢流堰式鱼道、潜孔式鱼道组合的组合式鱼道的水力特性，结果均表明组合式鱼道的水力学条件较好，适合不同习性和种类的鱼类通过。

溢流堰式鱼道隔板设计简单，但其堰顶形状、尺寸、外形及孔口布置都是需要研究的重要特征，因此，本文结合工程实例对堰-底孔组合式鱼道不同堰顶缺口布置的水流特征进行了研究，研究方法和思路可为同类型鱼道的设计提供借鉴。

1 数学模型建立

1.1 鱼道建模基本参数

堰-底孔组合式鱼道单个池室净宽2.0 m，长2.6 m，每间隔10个过鱼池设置一个长5.5 m 的平底休息池。鱼道全长720 m，鱼道梯级数117个，其中过鱼池106个，休息池11个。上游设计水位36.20 m，下游运行水位30.70 m，对应设计水头5.5 m 的鱼道设计流速为0.4～1.0 m/s，过鱼对象为四大家鱼等经济鱼类，流速基本满足过坝鱼类的喜爱流速范围。池内设两个底孔加一堰顶缺口的组合式隔板，隔板厚20 cm。隔板两底孔尺寸为0.3 m×0.3 m，底孔居中布置；堰顶缺口尺寸为1 m×1 m，在池室底板高程假定为0 m 时，堰顶缺口底边相对高程为1 m，相邻隔板交错布置。鱼道内设计水深为2 m，入口底板高程假定为0 m，斜坡段底坡1∶50，断面型式如图1所示。

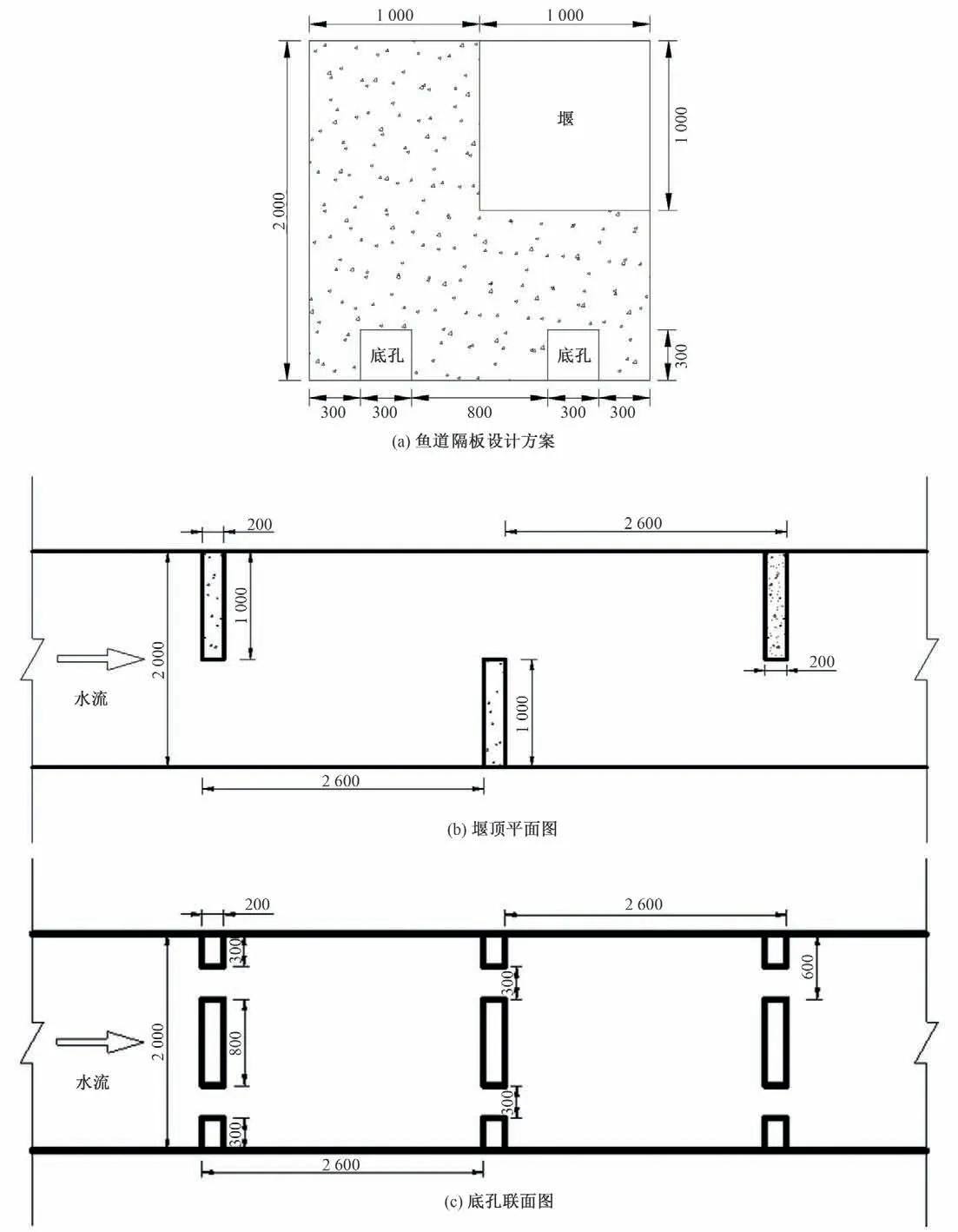
图1 鱼道细部尺寸Fig.1 Fishway detail size

研究中选取靠近下游的10 个池室，9 个隔板建模，池室编号从下游到上游按鱼类洄游路线编号为1～10号，下游进口处设为1号池室，上游为10号池室。底孔编号从下游到上游为1～9。

1.2 控制方程

鱼道内水流流动考虑是不可压缩水流流动问题，湍流模型选用标准k-ε模型。

数学模型控制方程包括连续性方程、动量方程和k-ε方程：

连续性方程：

动量方程：

紊动能k方程：

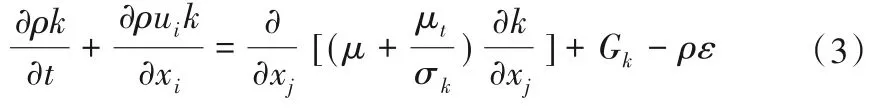
紊动能耗散率ε方程：

式中：t为时间，s；u、v、w为x、y、z方向的时均速度分量为坐标分量，m/s；ρ为水体密度，kg/m³；μ、μt为水体的黏性系数和紊动涡黏系数，m2/s；p为时均压强，Pa；gi为重力加速度，m/s2；k为紊动能，m2/s2；ε为紊动能耗散率，m2/s3；Gk为紊动能产生项，各项紊流常数取值为Cμ=0.09、σε=1.3、σk=1.0、Cε1=1.44、Cε2=1.92。

追踪自由液体表面采用VOF 方法，通过计算水和气的体积分数来表征物体的形态，aa表示气体的体积分数，aw表示水的体积分数，其控制方程如下：

1.3 网格剖分

鱼道池室水流条件计算网格划分的思路为：在形状复杂的区域采用四面体单元划分非结构网格，在形状相对简单的区域划分为六面体结构网格。由于使用壁面函数法，在划分网格时不需要在壁面区对网格进行加密。鱼道形状相对简单，为保证网格质量，计算区域采用六面体网格进行网格划分，隔板过鱼孔（堰顶缺口和底孔）局部加密。池室内采用网格尺寸0.1 m，隔板过鱼孔网格尺寸0.05 m，模型含54.45 万个节点，11.98 万个六面体单元，网格划分见图2。

图2 鱼道网格划分（从左到右1～10号）水流方向从右到左Fig.2 Fishway grid division（from left to right，1～10#）flow direction from right to left

1.4 边界条件

进出口边界条件设置为压力出口，采用进出口自由面水位作为边界条件；顶部边界条件设压力出口，压强为大气压；边墙和底板设为无滑移固壁边界。

1.5 数学模型验证

数学模型采用现场实测的池室水深和底孔流速进行验证，工况为现场监测实测的工况，上游水深1.38 m，下游水深0.39 m。水深测点为池室中间左右两侧，每个池室实测2 个测点，池室水深结果取2 个测点水深的平均值，底孔流速按水流方向分为左右底孔，以ADV声学多普勒流速仪测量测点速度大小及方向，结果见图3和图4。如图可见，数学模拟结果与现场实测的数据吻合较好，数值模拟可以比较准确地模拟鱼道池室内的水流流态。

图3 池室水深对比Fig.3 Comparison of Water depth of the pool room

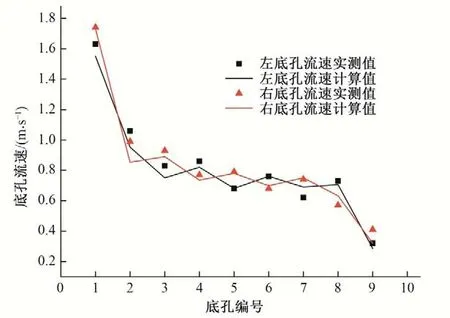
图4 底孔流速对比Fig.4 Comparison of the Bottom hole flow rate

1.6 计算方案

不同的堰顶形状会改变鱼道池室内的水流特征。如图5所示，堰顶缺口的宽度B为1 m 保持不变，相邻过鱼堰顶缺口交错部分长度为p，如图6，设无量纲参数p/B，分析p/B为0（方案1）、0.4（方案2）、0.6（方案3）、0.8（方案4）、1.0（方案5）在鱼道运行水深h=2.0 m 的水流结构，从方案1到方案5的p/B逐渐增大，上下池室堰顶缺口错缝偏移逐渐减小。p/B等于0时，堰顶缺口左右交错布置，p/B等于1时，堰顶缺口布置在隔板中间，隔板左右完全对称。

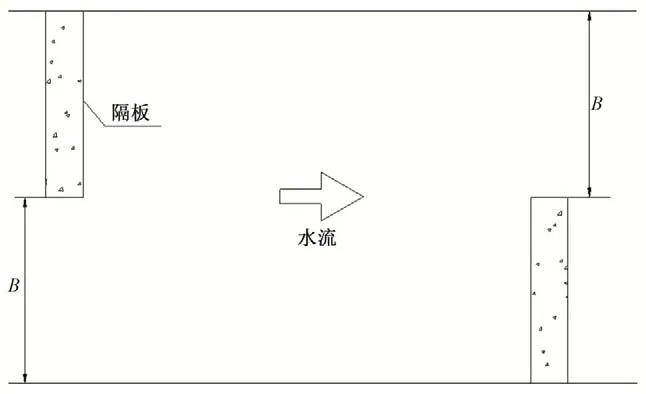
图5 p/B=0鱼道水池结构布置Fig.5 P/B=0 Structural layout of fishway pool

图6 p/B＞0鱼道水池结构布置Fig.6 p/B＞0 Structural layout of fishway pool

2 结果与分析

2.1 池室流态分析

堰-底孔组合式鱼道系溢流堰式鱼道和孔口式鱼道的结合，沿水深方向具有不同的水流流态。为了避免进出口边界对池室流态的影响，选取中间池室5号进行分析，考虑鱼类通过堰顶和底孔不同的洄游路线，选取两个不同水深的平面流场进行分析，两个平面分别位于距池底以上0.15 和1.5 m，0.15 m 处的平面流场能够反映两底孔的水流特征，1.5 m处的平面流场能反映堰顶的水流特征，图层位置示意图如图7所示。分析了5 种方案两个水层的流速分布，图8列出了方案1到方案5不同水层的流速分布和流速矢量图。

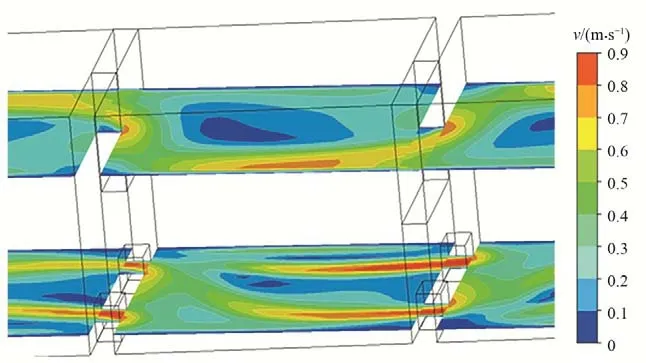
图7 不同水层流速云图三维模型（P/B=0）Fig.7 Three dimensional model of flow velocity cloud diagram of different water layers（P/B=0）

鱼类在进入鱼道进口后，其过鱼效果主要取决于隔板过鱼孔流速及池室内流态。要求过鱼孔流速小于过鱼对象的克流能力，池室内主流明确，有一定回流，但回流不能过于剧烈，范围不能过大，以免鱼类迷失方向，延误上溯时间［9，10］。

如图8（a）所示，p/B等于0 时，通过隔板堰顶进入下级水池的水流，上级鱼池水流通过堰顶缺口进入下级鱼池时受隔板横向导板作用，堰孔流出的水流偏向堰孔一侧，受下级隔板堰顶缺口影响在池室3/4 处开始偏向下级堰顶缺口一侧，水流沿边壁流动直到受到下一级隔板阻挡后改变方向，沿下一级隔板边壁流动。从流速矢量图来看，堰顶处水层主流明确，但存在明显的主流贴壁现象，主流的另一侧存在超过池室2/3 面积的大范围回流区，回流区的范围较大。从流速云图来看，最大流速0.76 m/s，出现在堰顶缺口前缘，主流在池室内流速超过0.6 m/s的区域主要位于堰孔附近和堰孔同侧边壁附近，池室内大部分区域主流流速约为0.4～0.7 m/s，回流区流速值不大，在0.1～0.3 m/s 之间，回流强度不大，能够满足四大家鱼等经济鱼类洄游要求。距离池底0.15 m 范围内的水流由底孔进入水池，如图8所示，在整个水池底部水深范围内形成了较大的回流区，底孔处最大流速达到0.93 m/s，两底孔的流速分布不均，远离堰顶缺口一侧底孔流速大于0.7 m/s的区域面积大于另一侧底孔。

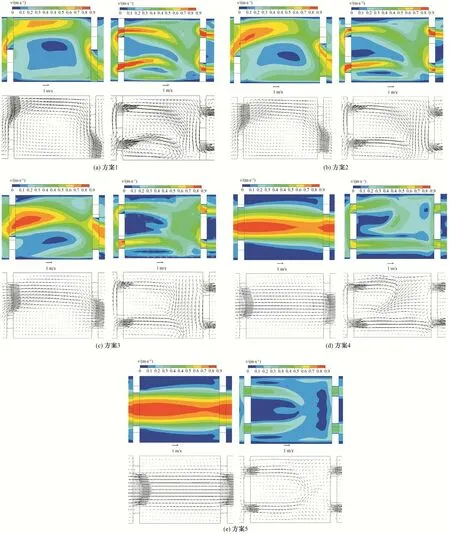
图8 不同方案下鱼道池室不同水层流态Fig.8 Flow pattern of different water layers in fishway pool chamber under different schemes

如图8（b）所示，p/B等于0.4 时，流速分布规律与p/B等于0时基本一致。堰顶处水层主流宽度与堰顶缺口宽度接近（堰顶缺口宽度1.0 m），主流最大流速增大至0.83 m/s，堰顶处水层主流明确，主流贴壁现象有所缓解，主流另一侧的回流区面积较P/B等于0 时略有减小。底孔处水层最大流速0.90 m/s，出现在远离堰顶缺口一侧底孔处，另一侧底孔处仍有较大面积的回流区。

如图8（c）所示，p/B等于0.6 时，堰顶处水层主流两侧回流区发生变化，回流区面积由原来的2/3 减少至约1/2，主流最大流速为0.96 m/s，堰顶处水层主流明确，相对于P/B等于0 时，主流弯曲程度小，主流平顺，基本没有主流贴壁现象。底孔处水层最大流速0.81 m/s，出现在远离堰顶缺口一侧底孔处，两底孔流速分布不均的现象有所改善，底孔主流的流速在0.5～0.7 m/s之间，回流区的流速小于0.3 m/s，各个水层流速分布满足不同种类、不同水层的目标鱼类上溯洄游要求。

如图8（d）和图8（e）所示，p/B大于等于0.8 时，堰顶处水层主流接近一条直线，主流宽度等于堰顶缺口宽度，在主流两侧形成两个面积较小的回流区。p/B等于0.8 时，主流最大流速1.17 m/s，p/B等于1.0时，主流最大流速1.38 m/s。底孔处水层的流速分布接近于对称，两底孔流速分布基本相同，P/B等于0.8底孔最大流速0.60 m/s，p/B等于1.0底孔最大流速0.47 m/s。p/B大于等于0.8 时，各个水层的主流明确，流态较好，但最大流速超过四大家鱼等经济鱼类洄游极限，对于部分游泳能力较弱的鱼类及幼鱼，可能会形成流速障碍。

方案2 到方案5 逐渐降低了上下池室堰错峰偏移，随着p/B增大，受隔板的阻碍作用逐渐减小，主流的弯曲程度减小，池室内回流区范围逐渐减少，但由于减小了隔板对水流的阻碍，能量耗散小，因此堰处主流流速逐渐增大。设计方案堰顶缺口居于隔板一侧，远离堰顶缺口一侧的底孔流速明显大于近堰顶缺口一侧的底孔流速，远离堰顶缺口一侧的底孔主流扭曲度大。优化了隔板的相对位置后，两底孔的流速逐渐接近对称，远离堰一侧的底孔主流逐渐明确，说明底孔的流态受堰顶缺口的布置方式影响。

2.2 堰顶处主流弯曲程度与衰减规律分析

最大主流流速沿程变化曲线一定程度上反映了流速衰减效果。如前所述，池室堰错缝偏移越大，池室内主流越弯曲。为了系统地分析池室内堰顶处水层主流流速的衰减规律，以池室5 号为研究对象，池室长为x轴，方向为水流流向，提取池室内主流流速的最大值，沿x轴方向绘制成图，各方案沿程流速如图9所示。

设参数1-Vmin/Vmax为最大衰减率，其一定程度上反映出水池内的流速衰减效果，各方案最大衰减率见表1，由图9和表1可以看出，主流流速衰减排序依次为：方案1＞方案2＞方案3＞方案4＞方案5。方案1 由于隔板对水流的阻碍作用，主流的最大衰减率最大为54.1%；方案2 到5 降低了上下池室堰错缝偏移，减少了隔板对水流的阻碍作用，其最大衰减率逐渐减少。

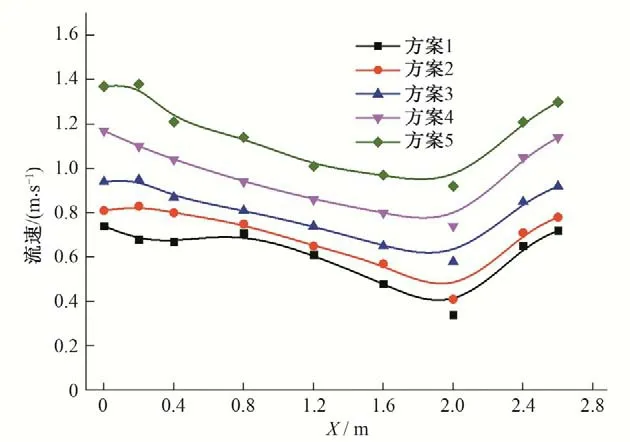
图9 堰处流速沿程分布Fig.9 Velocity distribution along weir orifice

表1 主流轨迹线流速最大衰减率分布表Tab.1 Distribution of maximum attenuation rate of mainstream velocity

2.3 推荐方案紊动能分析

鱼道中水流的紊动能过高，鱼类将消耗更多的能量，降低鱼类的游动能力和平衡能力，使其无法顺利完成上溯。适当的紊流动可为鱼类提供良好而稳定的水流条件，保证鱼类的上溯［11，12］。

图10列出了方案1和方案3堰顶处水层和底孔处水层紊动能分布图，由图可见，两种方案均是水流经过隔板堰顶缺口处紊动能达到最大值，紊动能在鱼道池室内总体较小。两种方案鱼道大部分区域紊动能均不超过0.06 m2/s2，满足过鱼对紊动能的要求。

图10 紊动能分布（单位：m2/s2）Fig.10 Distribution of turbulent kinetic energy

3 结 论

针对某堰-底孔组合式鱼道，建立鱼道三维数学模型，对不同的堰顶缺口布置方式进行分析，得出如下结论：

（1）上下池室堰顶缺口相对位置对池室流态影响较大。p/B越小，池室内主流越弯曲，回流区范围越大，此时鱼道池室内消能效果较好，堰顶处主流速度较小。通过增大p/B，能有效减少堰顶处主流弯曲程度，减小回流区范围。

（2）上下池室堰顶缺口相对位置对底孔的流速分布和流态具有显著影响。交错缺口的设置会使两底孔的流速分布不均，远离堰顶缺口一侧的底孔流速相对较大，底孔主流不明确。通过增大P/B，能改善底孔处流态，降低底孔流速。

（3）对于本工程而言，p/B=0.6 时，鱼道池室内流速分布合理，最大流速小于1.0 m/s，主流明确，回流区范围相对较小，池室内紊动能最大值为0.06 m2/s2，满足过坝鱼类上溯要求。 □