功率模式下水电机组最优滑模控制策略研究

乐绪鑫，张官祥，马 龙，杨廷勇，谭小强，金学铭，李超顺

（1.长江三峡能事达电气股份有限公司，武汉430072；2.中国长江电力股份有限公司白鹤滩电厂，昭通657000；3.华中科技大学土木与水利工程学院，武汉430072）

水电机组是电网中起调节作用的重要机组，其任务是提高电能质量，维持电网频率和功率的稳定。通常，水电机组需要频繁在不同运行工况之间切换，造成水轮机调节系统参数随工况点的改变而变化。而且，水轮机调节系统具有明显的非线性和非最小相位特性，导致其控制难度较大。传统的PID 控制器虽然具有结构简单和可靠性高的优点，但其在水电机组运行过程中往往采用固定的结构和参数，对工况变化的适应性较差，已难以满足机组优化运行的需要［1］。近年来，一些先进的控制策略，如模糊控制［2，3］、预测控制［4-7］和融合控制［8-10］等，在水轮机调节系统中的应用得到了快速发展并取得了一系列研究成果。然而，这些控制策略往往基于线性模型且抗干扰能力较差［11］。作为重要的鲁棒控制策略，滑模控制在实现水电机组优化运行方面具有巨大潜力［12-14］。

滑模控制本质上是一种非线性控制方法，与其他控制策略相比其特殊之处在于控制的不连续性。因此它能根据系统当前状态切换相应的控制规则，使系统按照预定“滑动模态”的状态轨迹运动并不断收敛到期望点。滑模控制器的“滑动模态”可以自行设计且与对象参数和扰动无关，所以它控制简单，对参数变化和系统扰动具有较强的鲁棒性。随着滑模控制理论体系的完善，滑模控制器已经被广泛用于工业生产，且控制效果较好。但滑模控制器在控制过程中存在抖振问题和“假稳定”现象。抖振问题会造成系统振荡甚至失稳，而“假稳定”现象会使水轮机调节系统这类非最小相位系统的系统变量无法持续跟踪给定值［15］。因此滑模控制理论在水电机组控制中的应用受到了限制。此外，多数滑模控制器设计是基于机组的转速控制模式，且不考虑永态转差系数，显然不满足对真机的控制要求。

通过以上分析可以看出，滑模控制理论在水电机组优化控制应用方面仍然有待发展。针对滑模控制器的固有缺陷和参数优化问题开展研究，不仅能促进滑模控制理论的发展，也加速了理论成果向实际应用转化。为此，本文基于自适应优化算法和综合目标函数，研究了滑模控制器的参数优化策略。进一步，结合实际电站机组的详细模型，以机组弱稳定工况为例，设计适用于功率控制模式的水电机组最优滑模控制器，并通过对比试验验证所设计的滑模控制器的性能。

1 水轮机调节系统建模

水轮机调节系统基本模型是研究系统精细化建模、稳定性以及优化控制的基础，主要包含水轮机、发电机及负荷、引水系统、调速器4 个基本组成部分，其结构框图如图1所示。本节根据实际水电站的特点和对象建模方法，建立了除控制器外的水轮机调节系统整体线性模型，为后续改进滑模控制器的设计奠定了基础。

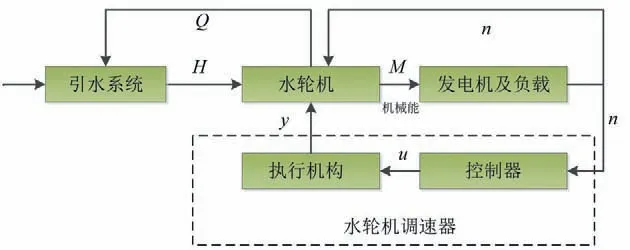
图1 水轮机调节系统结构图Fig.1 Structure diagram of hydro-turbine governing system

1.1 水轮机模型

在小波动运行工况下，混流式水轮机外特性模型可以近似用线性的水轮机力矩方程和流量方程表示如下：

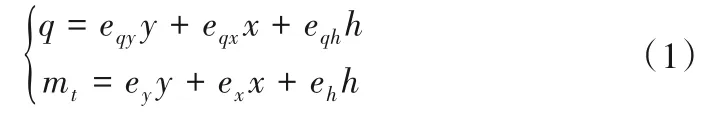
式中：q、mt、y、x和h分别为流量、力矩、导叶开度、转速和水头的偏差相对值；eqy、eqx和eqh分别为流量对导叶开度、转速和水头的传递系数；ey、ex和eh分别为力矩对导叶开度、转速和水头的传递系数。

1.2 引水系统模型

在小波动情况下，当水电站压力管道长度小于600～800 m时，可以忽略管壁和水体弹性以及水流流动的摩擦阻力。因此压力引水系统的数学模型采用刚性水锤方程表示如下：

式中：Tw为水流惯性时间常数，s；L为管道长度，m；Qr为额定流量，m3/s；Hr为额定水头，m；g为重力加速度，m/s2；A为管道面积，m2。

1.3 发电机模型

发电机模型主要有一阶模型、三阶模型和五阶模型。本文计及励磁系统动态和转子阻尼绕组作用但忽略q轴的G绕组，也不考虑定子暂态，故采用发电机五阶模型，用微分方程组表示如下：

式中：Ef为励磁电动势；E'q和分别为q轴暂态电势和次暂态电势；E'

d'为d轴次暂态电势；Td'0和分别为d轴开路暂态时间常数和次暂态时间常数；为q轴开路次暂态时间常数；Xd、Xd'和分别为d轴同步电抗、暂态电抗和次暂态电抗；Xq和分别为q轴同步电抗和次暂态电抗；Id和Iq分别为d轴和q轴的定子电流分量。

其中电磁力矩的计算方法为：

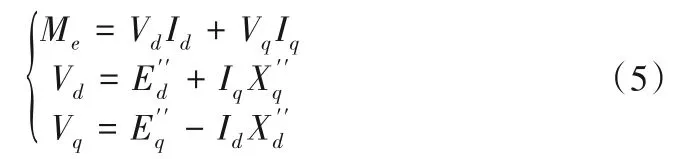
式中：Vd和Vq分别为机端电压Vg的d轴和q轴分量，

为分析方便，本文采用不考虑PSS（电力系统稳定器）作用的一阶励磁系统简化模型［16，17］，如式（6）所示。

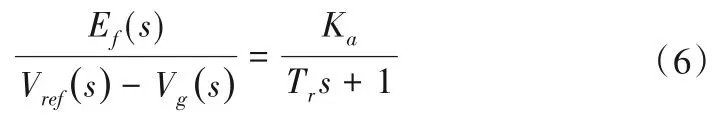
式中：Ka和Tr分别为等效的励磁系统增益和时间常数。

1.4 调速器模型

水轮机调速器包括控制器和电液随动系统两个部分。目前国内外水电站普遍采用PID 调节规律的控制器，包括并联PID 和串联PID 两种结构。本文的目的是为水轮机调节系统设计改进滑模控制器，故在此不考虑PID 控制器。对于实际水电机组的调速器，电液随动系统由主接力器、配压阀、电液转换器等元器件组成，忽略死区、饱和、间隙、限速以及延迟等非线性环节，其结构框图如图2所示。

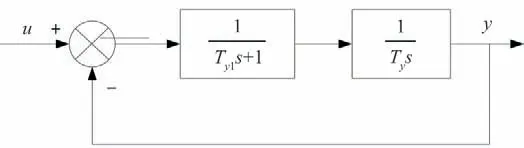
图2 水轮机调速器随动系统结构图Fig.2 Structure diagram of hydraulic turbine governor servo system

根据上述结构框图可求得水轮机调速器电液随动系统的传递函数如式（7）所示。

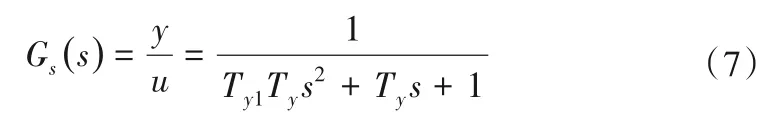
式中：Ty1和Ty分别为中间接力器和主接力器的反应时间常数。

1.5 电力网络模型

电力网络包括互连的输电线路和变压器，它们均可以用π型等值电路进行建模。在功率控制模式下，电网侧可近似为无穷大电力系统，相应的网络方程为：

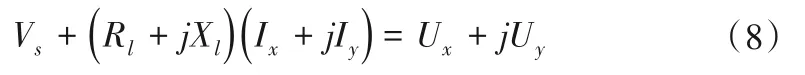
式中：Rl为变压器和线路的电阻之和；Xl为变压器和线路的电抗之和；为无穷大母线电压；Ix，Iy为网络电流；Ux，Uy为网络电压。

需要指出的是，电力网络模型建立在网络的复坐标系(x，y)中，而发电机方程建立在发电机的正交坐标系(d，q)中。由于发电机的q轴相对于网络的实轴偏移一个功角δ，因此两个坐标系之间的变换关系为［18］。

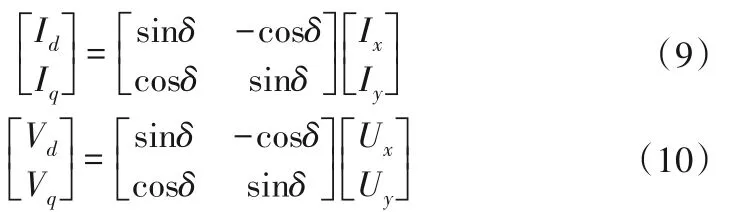
式中：Ix，Iy和Ux，Uy分别为复坐标系(x，y) 中的网络电流和电压；Id，Iq和Ud，Uq分别为正交坐标系(d，q)中的网络电流和电压。

2 最优滑模控制器设计

2.1 功率模式下水电机组滑模控制器设计

通常，状态变量的微分方程可由传递函数变换得到，状态变量与代数变量的关系需要利用泰勒展式将代数方程局部线性化，并忽略二阶以上高阶微量得到。根据上一节水轮机调节系统各子系统的基本方程，利用泰勒展开公式将代数变量局部线性化得功率控制模式下不包含控制器的水轮机调节系统的状态空间方程，见式（11）。

式中：h1为中间变量，且；系数K1～K13见式（12）和式（13）。

为便于设计滑模控制器，将式（11）表示为式（14）所示。

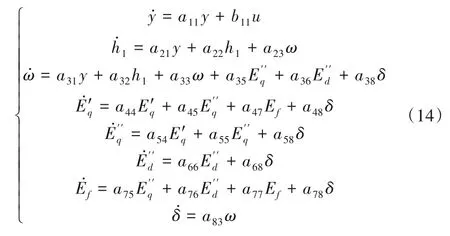
在功率控制模式下，设转速给定为ωd、功率给定为pd且ep≠0，则系统跟踪误差及其导数为：

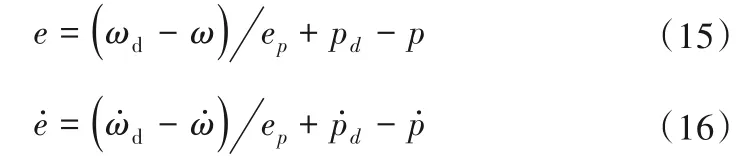
定义滑模面函数为：

上式两边同时对时间求导，得：

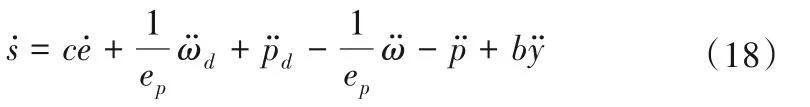
为求解等效控制律，将（14）式第一项两边同时对时间求导，得：

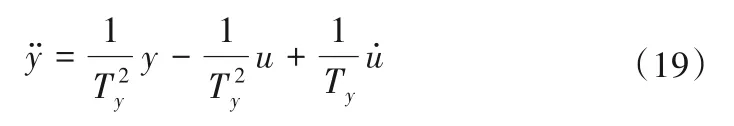
同时，将（14）式第三项两边同时对时间求导，得：

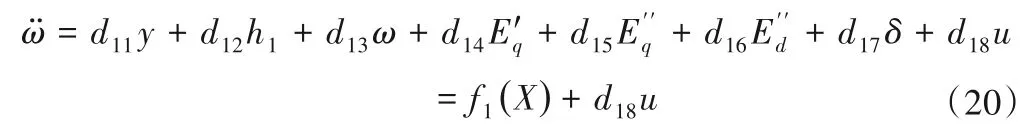
式中各系数表示如下：

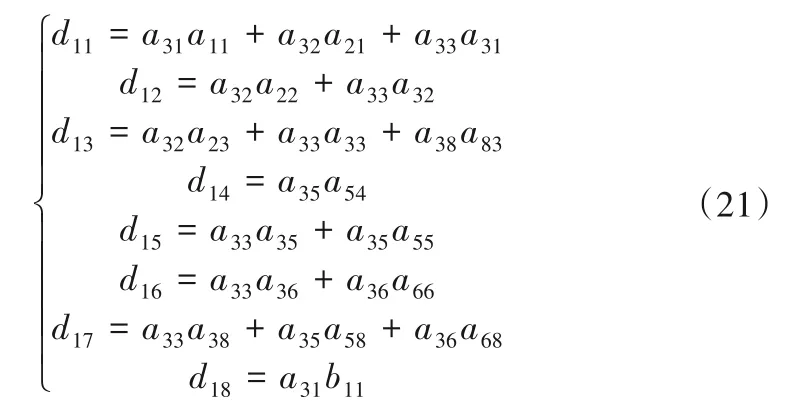
由于机组并入无穷大电力系统运行，机组转速基本不变，此时有功功率近似等于电磁力矩，即Pe≈Me。因此由式（11）可得：

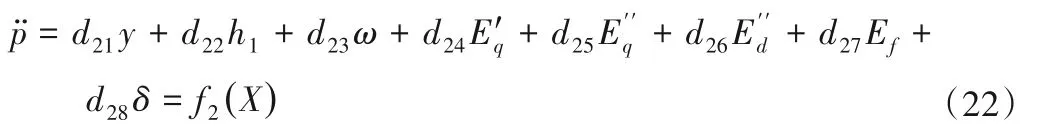
式中各系数表示如下：

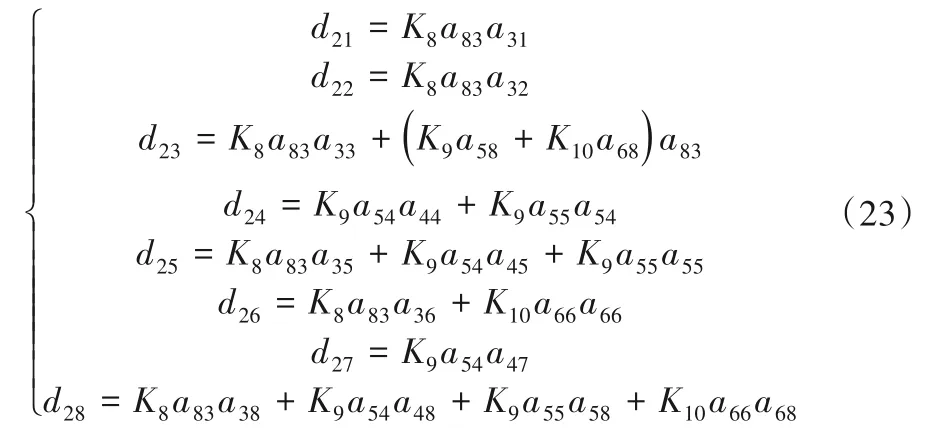
将式（19）、（20）和（22）代入式（18），有：

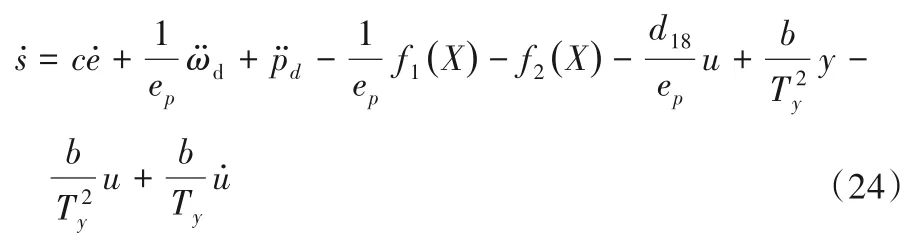
令= 0，则等效控制律为：

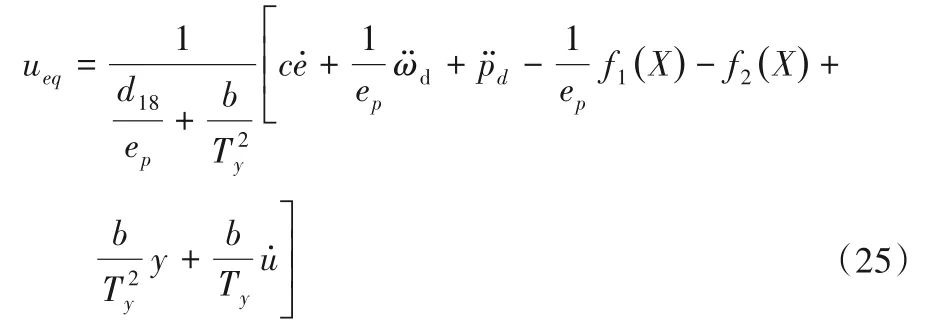
采用指数趋近律，且以饱和函数替代符号函数，则切换控制律为：

结合式（25）和式（26），改进的滑模控制律为：

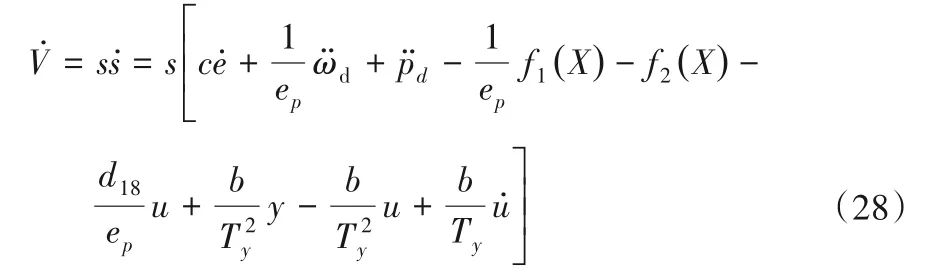
将式（27）代入式（28）得：

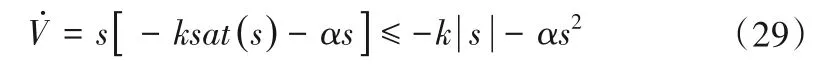
由于k，α> 0，因此≤0 恒成立。根据Lyapunov 稳定性定理，闭环控制系统渐进稳定，s在有限时间内是渐进收敛的，即当t→∞时，s→0，收敛速度取决于k和α。

2.2 滑模控制器的参数优化

控制器的设计离不开参数优化。基于设计好的滑模控制器，本小节提出了一个通用的控制器参数优化策略。它主要包含目标函数的确定和优化算法的选择两个重要组成部分。目标函数的定义决定了控制器参数优化的效果，一般来说可采用计算简单且物理含义明确的局部性能指标和全局性能指标作为优化的目标函数。但此类指标通常单独作为目标函数使用，对控制效果的评价过于单一，难以综合衡量控制器的优劣。为克服传统目标函数的缺点，引入一种混合目标函数，包含以下4种性能指标：

（3）系统输出信号的反调量：mr。

（4）系统输出信号的超调量：mo。

其中，指标（2）主要对控制量进行限制，指标（3）和（4）的目的分别是抑制系统变量的反调量和超调量。对上述性能指标进行组合，混合目标函数可表示为：

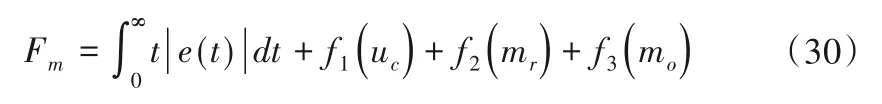
其中，子函数f1、f2和f3分别为：

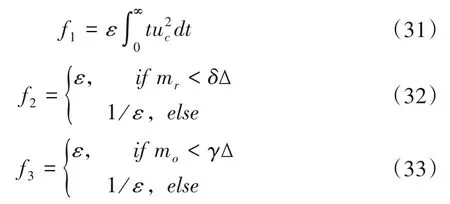
式中：uc为控制量；∆为控制目标的变化量；δ为允许的最大反调量占控制目标变化量的比例；γ为允许的最大超调量占控制目标变化量的比例；ε为正常数，其值很小，可取10-3。

考虑到不同优化算法参数会对算法性能产生影响，本文采用无参数的自适应模糊粒子群算法（AFPSO）优化控制器参数，以避免参数选择的困难。因此，基于混合目标函数和自适应模糊粒子群算法，本文提出了针对改进滑模控制器参数优化的通用框架，如图3所示。

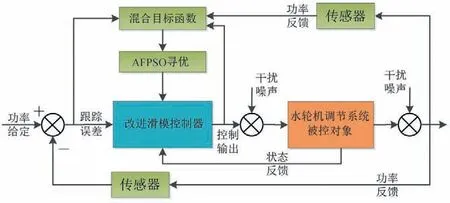
图3 基于AFPSO的水电机组改进滑模控制器参数优化示意图Fig.3 Schematic diagram of parameter optimization of AFPSO based improved sliding mode controller for hydropower units

3 试验对比及分析

本节分别在三种不同试验条件下测试所提出针对功率模式的最优水电机组滑模控制器及其参数优化策略的鲁棒性和优越性。用于对比的控制器分别为由电站实际控制参数确定的PID控制器和由Zieglar-Nichols（Z-N）法整定的PID控制器。

用于水轮机调节系统仿真的工况参数为：工作水头H=202 m；导叶开度Y=35.4%；水轮机传递系数eh=1.226 3、ey=1.642 0、ex=-1.349 1、eqh=0.432 1、eqy=1.592 0、eqx=-0.340 2；引水系统水流惯性时间常数Tw=0.579 2。混合目标函数中参数设置为δ=0.1、γ=0.02。3种对比方法的控制器参数设置如表1所示。

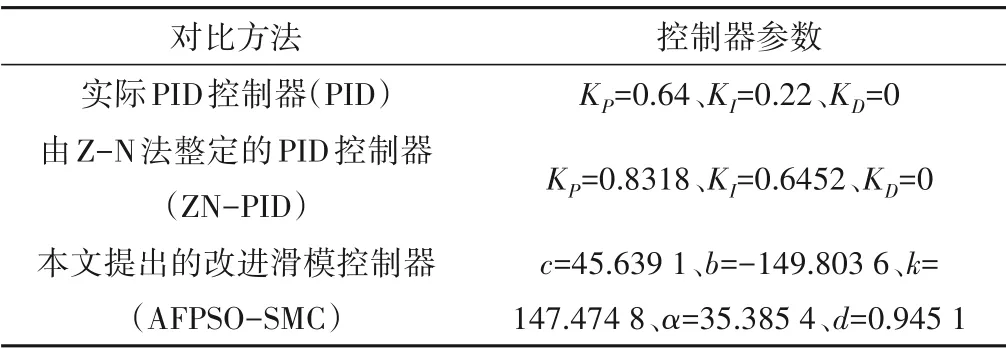
表1 不同方法的控制器参数Tab.1 Controller parameters of different comparison methods

3.1 参数摄动试验

在功率控制模式下，考虑到机组的参数在运行中会随工况发生不同程度的变化，可能对控制器的鲁棒性和控制性能产生一定影响，因此设计了参数摄动试验［19，20］。由于引水系统参数与机组的水头和流量密切相关，具有发生较大变化的可能性，因此选择Tw作为目标参数。保持系统其他参数（包括控制器参数）不变，仅将Tw的值减小为原始值的90%（即10%摄动量）和70%（即30%摄动量），分别对3 种控制器作用下的水轮机调节系统进行仿真，得到的功率阶跃响应曲线如图4所示。可以看出，摄动量较大时3种控制器的超调量和反调量均有所减小，但相应的调节时间均有所增加。AFPSO-SMC 控制器在不同参数摄动下均具有最小的超调量和反调量，综合性能最好。PID控制器尽管反调量较小，但上升时间和调节时间均最长，难以满足快速调节要求。ZN-PID 控制器尽管上升时间较短，但反调量和超调量均较大，这对系统会造成不小的冲击。

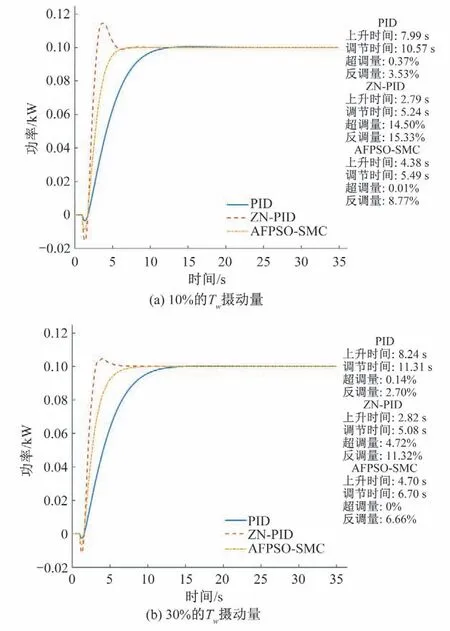
图4 参数不同摄动下的各种控制器性能对比Fig.4 The performance comparison of various controllers under different perturbations of parameter

3.2 阶跃响应试验

在功率控制模式下，考虑到机组在运行过程中功率可能会因为功率给定变化和负载变化而做出适应性地调整，因此设计了阶跃响应试验。为充分激发系统的动态特性，选择阶跃信号作为功率或负载给定信号。保持系统所有参数（包括控制器参数）不变，实施功率给定值或负载给定向上阶跃10%，分别对3种控制器作用下的水轮机调节系统进行仿真，得到的功率和负载阶跃响应曲线如图5所示。可以看出，在两次试验中AFP⁃SO-SMC 控制器的上升时间和调节时间均明显快于电站实际控制器，且反调量和超调量均在理想的范围内。ZN-PID 控制器尽管上升时间较短，但超调量和反调量均不满足要求。同时，过大的超调量也引起了机组转速和功率的振荡，不利于系统的稳定运行。

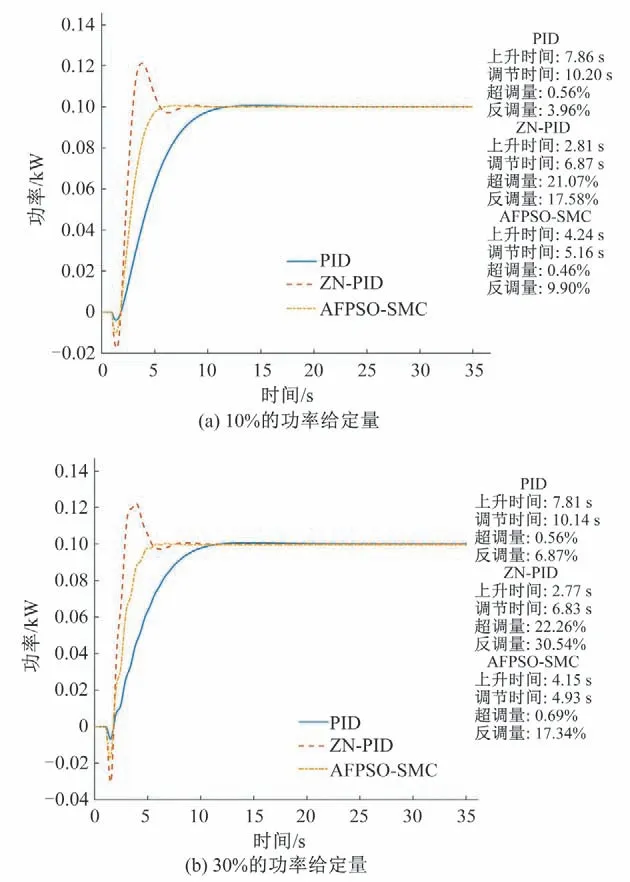
图5 不同阶跃扰动下的各种控制器性能对比Fig.5 The performance comparison of various controllers under different step perturbations

3.3 噪声干扰试验

在功率控制模式下，考虑到机组的状态信号在采集的过程中难免混杂着不同能量的环境噪声，可能造成控制器在进行数学运算时出现不准确甚至异常的计算结果，进而恶化控制品质，甚至引起系统的失稳，因此设计了噪声干扰试验［21］。为尽可能模拟不同能量水平的环境噪声，选择具有不同信噪比的高斯白噪声作为干扰源。保持系统所有参数（包括控制器参数）不变，对3 种控制器作用下的水轮机调节系统进行功率阶跃扰动，在仿真中对各子系统的输出分别施加信噪比为30 dB 和40 dB 的噪声，得到不同噪声水平下的功率响应曲线，如图6所示。可以看出，PID 控制器和滑模控制器均对不同程度的噪声干扰具有很强的鲁棒性。同时，控制器的鲁棒性没有受到不同的优化算法和控制参数条件的显著影响。

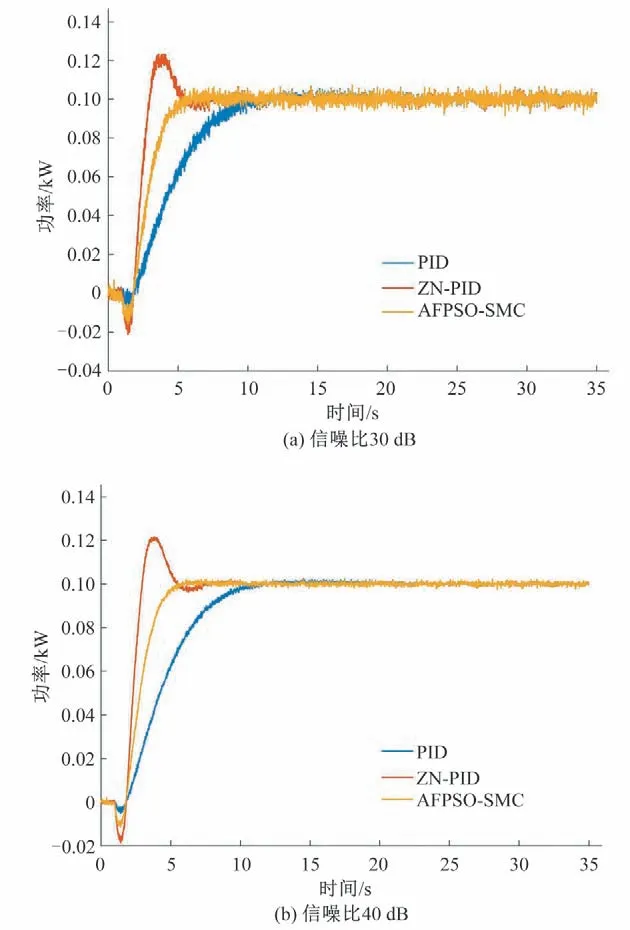
图6 不同噪声水平下的各种控制器性能对比Fig.6 The performance comparison of various controllers under different noise levels

4 结 论

本文基于水轮机调节系统详细状态空间方程，设计了适用于功率控制模式下的水轮机调节系统滑模控制器，并依据提出的混合目标函数研究了控制器参数优化策略。为验证所设计的最优滑模控制器的有效性，在机组弱稳定工况下，通过设计参数摄动、扰动响应和噪声干扰实验进行对比验证，结果表明实际电站PID 控制器尽管反调量较小，但上升时间和调节时间均最长，ZN-PID 控制器上升时间和调节时间最小，但反调量和超调量都最大，而AFPSO-SMC 控制器在不同参数摄动、扰动响应以及噪声干扰下均具有较小的调节时间和超调量，综合性能最好。□