土壤渗透系数各向异性对我国西南山区小流域产汇流过程的影响研究

陈苍乙，冉启华，刘 琳，潘海龙，叶 盛

（浙江大学建筑工程学院水文与水资源工程研究所，杭州310058）

1 研究背景

山区流域地势陡峭，暴雨频发，容易在短时间内形成较大洪水，可能导致山洪、泥石流等地质灾害，严重威胁着人民群众的生命财产安全。山区流域降雨产流水文响应过程是山洪形成的基础，也是目前山洪相关研究的核心科学问题之一。鉴于山洪成灾快、破坏力强等特点，也为更全面地认识这些因素对山洪的影响，数值模拟常作为一种有效手段来研究山洪发生过程。土壤饱和渗透系数表征了土壤的下渗能力，是影响降雨径流过程非常重要的物理量，通常被作为数值模拟的一个关键参数。在自然界中，土壤渗透系数通常具有各向异性，一般用各向异性比（Kr）来表示，即水平方向（Kh）和垂直方向（Kv）饱和渗透系数的比值（Kh/Kv），可能是由土层层状或片状构造［1］、沉积过程和复杂的应力加载［2］等原因所导致的。关于土壤渗透系数各向异性的具体大小，目前学者的研究尚未形成一致。有研究表明，土壤的渗透系数在垂直方向上高于水平方向［3-5］；但也有研究得出相反的结论，水平方向的渗透系数高于垂直方向［6，7］。Terzaghi和Scott发现，重复层状土壤的渗透系数比较大，可达到100［8，9］；C Germa 'n Soracco 等［10］也发现土壤样品顶层15 cm 存在各向异性，水平方向的渗透系数约为垂直方向的5倍。

针对土壤渗透系数各向异性带来的影响，现有已有一些学者对此进行了研究。胡瑞等［11］发现在各向异性假设下，随着水平渗透系数的增加，单宽流量明显增大。周鹏鹏等［12］建立了我国南方某地下水水流数值模型，结果表明，随着各向异性比Kr的增大，洞室涌水量增加。曾文西等［13］发现在同一雨型作用下，Kr越小，雨水入渗深度越大。Yu等［14］指出Kr增加会导致边坡入渗能力和安全系数的降低。然而由于流域性质和水文过程的复杂性和异质性［15］，较多水文模拟案例中为简化模型分析计算过程均将土壤渗透系数设定为各向同性（Kh/Kv=1）。而上述相关研究表明，这种简化可能会导致无法准确估计流量、洞内涌水量和边坡安全系数等结果，进而可能造成严重的社会、经济后果。

为进一步明确土壤渗透系数各向异性在降雨径流过程中的影响，本文运用一种基于物理概念的水文数值模型，对我国西南山区碱坪沟流域的降雨径流过程进行了模拟。设置了不同土壤渗透系数各向异性的情景，系统性分析了渗透系数各向异性对流域土壤水分运动以及产汇流过程的影响。

2 研究区域

考虑到山洪灾害的频率、汶川地震影响等因素，本研究选用位于四川省都江堰市西北部的龙溪河流域作为研究区域，并选择龙溪河流域内的支沟碱坪沟流域进行详细研究。

龙溪河属于长江流域岷江水系（图1），碱坪沟为龙溪河中游左岸的次级支沟［16］。碱坪沟流域面积约3.5 km2，海拔为1 050～2 199 m，坡面的平均坡度为31.7%。整体自东北向西南方向延伸，主沟长1.7 km，整个流域被森林覆盖，平均纵比降36.3%［17］。碱坪沟地质构造复杂，断裂较为发育，出露的地层主要有震旦系灰绿色安山岩、凝灰岩及安山玄武岩和第四系地层，其中第四系地层主要为第四系残坡积层，岩性为含碎石粉质黏土［18］。气候为亚热带湿润气候，都江堰市年降水量约1 134.8 mm，主要集中在5-9月，占到全年降水量的80%以上，产流方式以蓄满产流和地下潜流为主［16，19］。

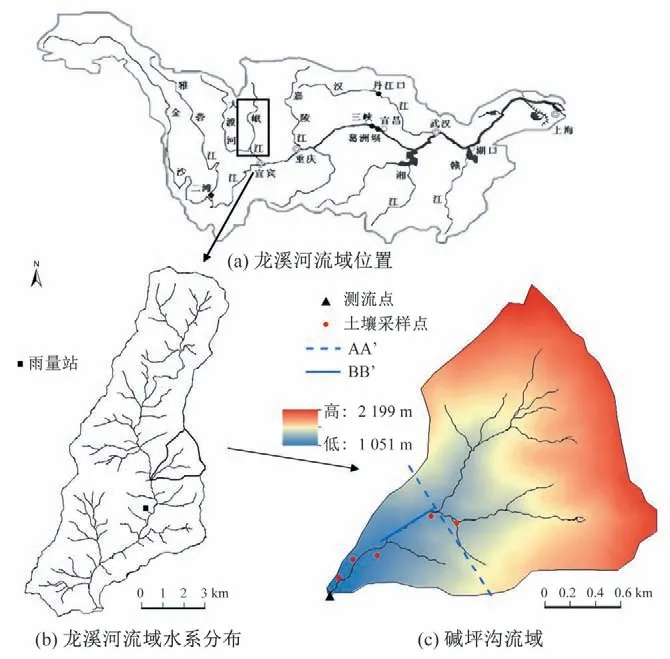
图1 研究区域地理位置及水系分布Fig.1 Location and river network of study area

3 数据与研究方法

3.1 数 据

本研究使用的水文数据包括碱坪沟流域2018年6月24日至7月21日雨季实测降雨和径流数据。降雨数据由JBD-2 翻斗式雨量计每1 min 采集一次。流量数据利用基于大尺度粒子图像测速（简称LSPIV）和立体视觉（简称SI）的流速面积法计算得到，测算精度为45 min/次，在本研究中将该方法所得的流量值作为实测流量数据使用。该方法将大尺度粒子图像测速技术与立体视觉技术相结合，组成一套完整的测流计算系统（SILSPIV），旨在实时非接触式获取河道断面的水位、表面流场和断面流量等要素［20］。SI-LSPIV 系统用于流量测算的准确性已在之前的研究中得到了验证［21，22］。

为了解碱坪沟流域内土壤渗透系数实际情况，在综合考虑流域地形及道路等客观因素后，研究人员从上游到流域出口共选了5 处较有代表性的地点采集土壤样品，沿深度方向在每个点的10～50 cm 和50～100 cm 两个范围内使用环刀分别从竖直向和水平向采集用于测量土壤饱和渗透系数和孔隙度的原状土样，密封保存后带回实验室。采用恒定水头法测定土壤饱和渗透系数，用饱和浸泡法测定土壤孔隙率。受地质条件限制，土壤采样难度较大，仅在其中4 处地点同时采集到了用于纵向渗透系数（Kv）和横向渗透系数（Kh）测试的原状土样。实测结果（表1）表明每组样品的纵向和横向渗透系数均有差异，由此可以得出，碱坪沟流域土壤渗透系数确实存在各向异性。

表1 各采样点土壤纵向和横向渗透系数对比Tab.1 Comparison between vertical and horizontal hydraulic conductivity of sampling points

3.2 InHM模型介绍

本文所用的模型为基于物理概念的分布式水文模型InHM（Integrated Hydrology Model），该模型最初在1999年由Waterloo大学的Vander-Kwaak 开发［23］。模型能够在不预设产流机制的前提下，用基本物理定律来描述产流的自然过程。可模拟地下水在饱和和非饱和区的三维流动、地下水在大孔隙中的三维流动、地表水二维坡面流动及二维河道流动等［24］。目前已被成功应用于泥沙运动模拟［25-28］、流域尺度下的地貌演变研究［29］、小尺度下水文响应模拟［30-34］等领域。

地表的瞬时流（包括坡面流和明渠流）是通过二维的浅水方程的扩散波近似计算。该二维地表水流被概化为第二种连续介质，通过一层厚度为as的水体覆盖在地下土体上与地下饱和/非饱和多孔介质互动。地表浅水深度为ψs，则地表水流的流动可以表述为：

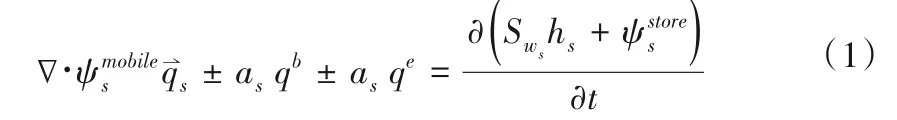
式中：qb为各种边界上的源/汇速率，s-1；qs为地表水流速度m/s；qe为地表和地下的水量交换速率，s-1；t为时间，s；hs为网格中未显示的地表微地形的平均高度，m；Sws为地表饱和度；ψsmobile和ψsstore为贮存水深和流动水深，m。

地下水在地下孔隙介质饱和/非饱和土体和大孔隙（两者均为地下连续体）中的流动在InHM 模型计算中通过Richards 方程表示：

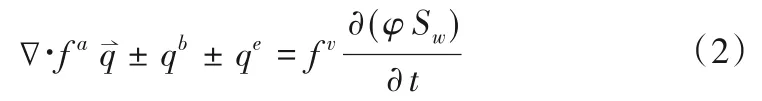
式中：φ为孔隙率；Sw为土壤饱和度；fa为各介质所对应的面积百分比，%；fv为各介质所对应的体积百分比，%；q⇀为达西流量，m/s。

关于InHM 的详细描述，请参阅Vander Kwaak［23］和Heppner［25］。

3.3 模型设定

基于碱坪沟流域的5 m 精度DEM 数据，提取出流域的河道，并在此基础上生成模型所需的三维网格（图2）。流域边界的网格水平精度为100 m，河道的网格水平精度为10 m［35］。根据对流域的实地观测，网格垂向上总共分为三层：表层为第四纪地层土壤（0～0.5 m），网格垂向精度为0.1 m；中间为透水碎石层（0.5～3 m），网格垂向精度为0.5 m；底部为不透水基岩层（3～13 m），网格垂向精度为2 m。

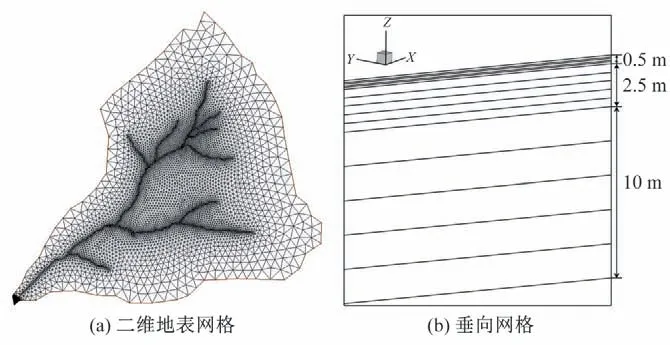
图2 碱坪沟流域模型网格Fig.2 Finite-element meshes for the Jianpinggou catchment

对龙溪流域的土壤调查表明，土壤性质与植被类型密切相关［36］。碱坪沟流域中的植被分布与海拔高度相关，因此将表层土壤按照海拔高度进行分区：1 300 m 以上、1 180～1 300 m 和1 180 m 以下。模型中表层和碎石层土壤的饱和渗透系数和孔隙率从土壤样品实测值中取平均值，基岩层的饱和渗透系数和孔隙率分别设定为1×10-8m/s和0.3（表2）。

表2 模型设定中的土壤饱和渗透系数和孔隙率Tab.2 The porosity and saturated hydraulic conductivity used in the model

土壤含水率与压强水头及相对渗透率的关系基于van Genuchten 方法［37］由模型率定获得。地表的Manning 糙率系数由下式［38］计算：

式中：Cv为地表植被覆盖率，以小数形式表示。

本研究中，碱坪沟流域的植被覆盖率假定为90%，经计算Manning系数为0.6。

为了使正式模拟开始时流域内的含水量尽可能接近流域实际情况，模拟前先对全流域进行20 d 的预模拟，选取流域出口处流量与实测流量近似的时刻作为正式模拟研究的初始时刻。

3.4 模型率定验证

考虑到像碱坪沟这样的山区流域存在山洪暴发的风险，该模型按洪水事件进行模拟，以便更好地了解对山洪的影响。为此，选取了7 场洪水场次，其中4 场用于率定，3 场作为验证工况。洪峰流量作为山洪预报的关键特征之一，以此为根据进行了率定和验证。在实测径流特征数据的基础上，通过调整土壤特征曲线参数，模拟了流域出口处的洪峰流量。图3展示了所选事件的观测值和模拟值的对比，Qobs为观测值，Qmod为模拟值。可以看出，该模型在水文过程模拟中表现较好，NSE值分别达到了0.88 和0.89，模拟结果基本能够代表实际水文响应结果，可以此为基础进行进一步的分析研究。率定参数α和β分别为0.13和2.2。

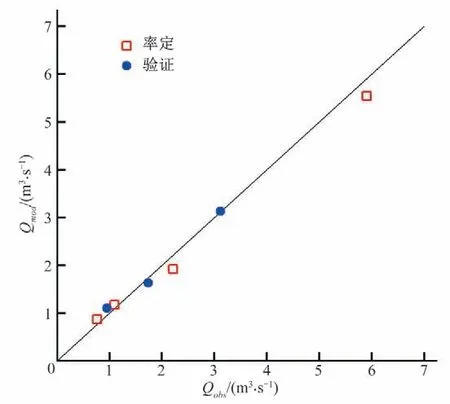
图3 洪峰流量观测值与模拟值的对比Fig.3 Comparison between the observed and simulated peak runoff for the selected events

3.5 工况设置

为了研究土壤渗透系数各向异性对产汇流的影响，我们对各向异性比进行了敏感性分析。由表2可知，中间层的渗透系数相对较大，对土壤水分运动的影响也相对更突出，因此本文重点研究中间透水碎石层土壤渗透系数各向异性的影响。根据表1实测数据各向异性比大小，本研究对碎石层设定了6 种不同各向异性比的工况以覆盖实际可能出现的情况，以及1 种渗透系数各向同性（Kh/Kv=1）的基础工况（表3）。每种工况均采用相同的降雨事件。

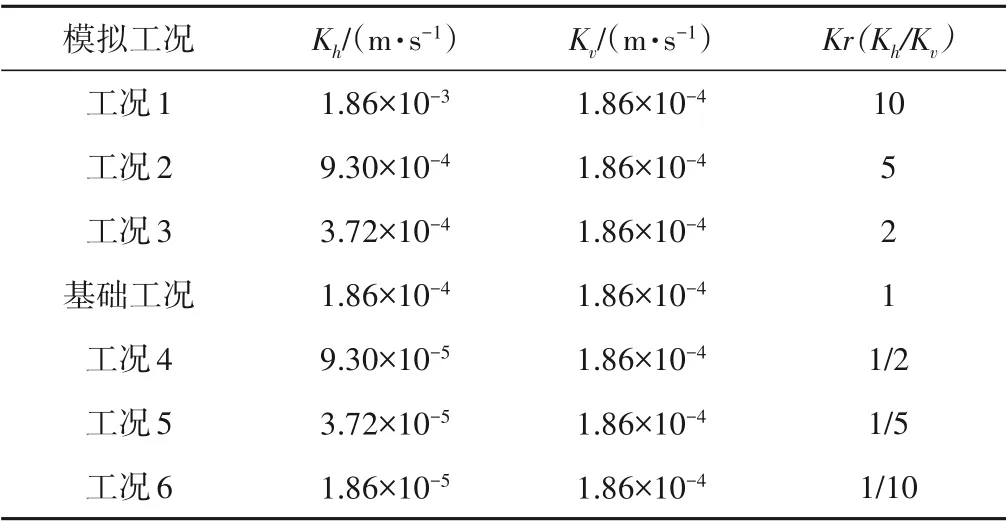
表3 不同各向异性比工况Tab.3 The simulated scenarios with different anisotropy

4 结果与讨论

4.1 渗透系数各向异性对汇流过程的影响

图4为不同Kr值下流域出口处的汇流过程流量曲线。从图中可以看出，不同Kr值对流域出流有很大的影响，且随着Kr的增大，峰值流量和总流量均增大。在渗透系数各向同性情况下（基础工况），峰值流量为5 m3/s，总流量为5 138.6 m3。当Kr为10 时，峰值流量可达8.5 m3/s，比基础工况高出约70%；总流量可达14 350.3 m3，是基础工况的近3 倍。当Kr很小（即Kr=1/5）时，总流量为2 413.4 m3，不及各向同性工况下总流量的1/2。由此可见，在不改变其他土壤参数的情况下，汇流过程对渗透系数各向异性非常敏感。这一汇流特性可认为与该流域下垫面条件有关。改变土壤横向渗透系数可能会使得地表径流和地下径流交互水量改变，也可以改变土壤水分运动的流速，峰值流量和流域出口处总径流量因此而改变。

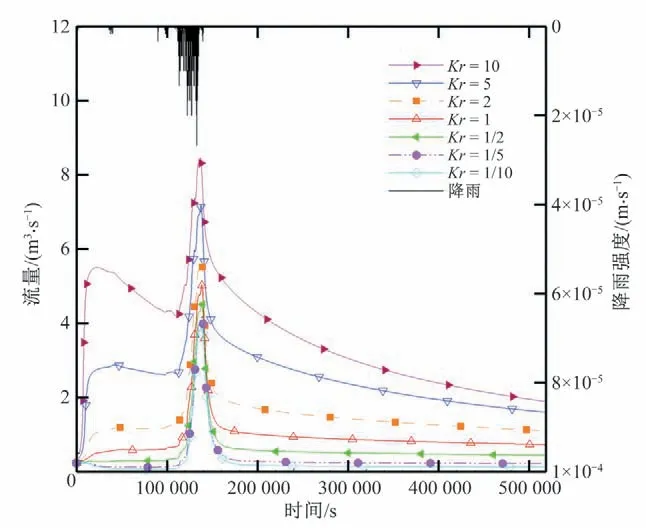
图4 不同Kr下流域出口处汇流过程线Fig.4 Simulated hydrograph at the outlet under different scenarios

此外，随着Kr的增加，初始水文响应过程对相同降雨事件变得更加敏感。当Kr小于1 时，初始径流量波动不大；当Kr大于1 时，初始水文响应出现一个较小的流量峰值。这种敏感性的上升可能是由于横向土壤渗透系数的增加，横向导水性越大，水流越容易在土壤中水平流动，土壤含水层中储存的水分也就会越多地出流，使得起始时刻流量迅速增加。因此，若不考虑各向异性，容易对初始水文响应产生不准确的估计。

图5为Kr与洪水事件特征参数之间的散点图。随着Kr的增加，到达峰值流量的时间逐渐减少。对比工况1（Kr=10）和工况6（Kr=1/10），峰现时间相差1 586 s，约为26 min。这段时间对于山洪的早期预警是至关重要的，在山区洪水监测预报的实际应用中，如果不考虑土壤渗透系数的各向异性，可能导致预警延迟，对人身财产安全造成严重的危害。

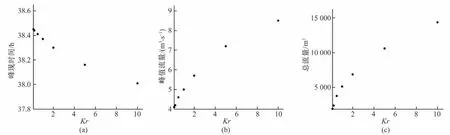
图5 不同Kr下的峰现时间、峰值流量及总流量Fig.5 Scatter plots between the anisotropic ratio（Kr）and time to peak discharge，peak discharge and total discharge

4.2 渗透系数各向异性对产流过程的影响

4.2.1 渗透系数各向异性对地表水深空间分布的影响

由图6所示的地表水深空间分布可知，地表水深D也随Kr变化。随着Kr的增大，流域源头地表水深逐渐降低，因为水流横向流动速度增大时，坡面上的水下渗进入土壤中后加快汇聚至河道。同时，从图6也可以看出，虽然地表产流面积较小，但河道水深较大。在渗透系数各向同性工况下，流域出口处水深为0.89 m；当Kr为10 时，水深1.43 m；当Kr为1/10 时，水深0.77 m。由此可见，在不同Kr值情况下，流域出口处水深差值相差较大。考虑到碱坪沟陡峭的地形条件，河道周边区域通常是海拔相对较低处，坡面上的降雨入渗后，形成的地下暴雨径流自坡顶汇流至河道及其周边并出渗，汇集到河道中，使得河道及其周边地表水深较大。

4.2.2 渗透系数各向异性对坡面土壤水分运动的影响

为了直观展示土壤渗透系数各向异性带来的影响，图7给出了峰现时刻剖面AA'处［图1（c）］的流速和流向分布情况。剖面AA'位于上游两条支沟汇合处河道南岸坡面上，与下游主河道垂直。由于断面处于相对平坦的区域，位置水头的影响有限，水流运动主要由压力水头驱动。图中标有箭头的曲线表示水流方向，流速用不同的颜色体现；横向实线为土壤表层、中间透水碎石层和不透水基岩层的分界线。

由图7可看出，各工况下流速均在中间透水碎石层与底部不透水层交界处达到最大，由地表至交界处流速逐渐增大，然后往更深层逐渐减小。渗透系数各向异性比的不同对流速有着显著影响，水流速度随着Kr的增大而增大，最大和最小Kr的工况各自对应的最大流速相差近一个数量级。

除了流速之外，水流运动方向也随Kr变化。在基础工况中［图7（d）］，土壤表层和中间碎石层中的水下渗至不透水基岩层的交界面，此时流速达到最大，随后沿着地形坡度流动。但随着Kr的增大，中间碎石层与不透水基岩层交界面处的流速明显增大，流向逐渐向偏向于平行地表的方向，因而土壤水分可能会被限制在一个相对较浅的深度［39］［图7（a），（b）］。而在Kr较小的情况下，水流基本不参与水平流动，大部分水体均垂直于地表入渗至更深的地方［图7（e）-（g）］。

图7很好地解释了图6的现象，当Kr增加时，在坡面上水流横向流动速度加快，流速方向也逐渐变为水平方向，增加了坡面排水量，进而促进了地表水的入渗，使地表水深进一步降低，大量地表水以及土壤中储存的水分出渗到河道形成径流，最终抬高了河道的水深。

4.2.3 渗透系数各向异性对河道土壤水分运动的影响

为了研究河道河床处的土壤水分运动，本文进一步研究了主河道纵剖面的流速分布［图1（c）中的BB'］，图8为主河道BB'纵剖面流速示意图。从图中可以看出，河道地形呈阶梯状，与图7中相对平缓的山坡不同，沿主河道的流速变化幅度较明显，在陡坡处流速较大，在平缓台面处流速较小。这种变化主要发生在表层和中间透水碎石层，基岩层的速度变化不大。随着Kr的增大，透水碎石层的流速逐渐增大。各向同性工况下，河道坡面地下暴雨径流的最大流速为2×10-4m/s；当Kr为10时，最大速度可以达到2×10-3m/s；而当Kr为0.1 时，最大流速可仅为9×10-5m/s。这种现象不论是在坡面上还是平台处均出现，说明了河道沿程的流速整体均随Kr增加而增加。

图7 AA′纵剖面流速流向示意图Fig.7 Longitudinal profile of flow velocity and flow direction under different Kr scenarios

图8（h）是基础工况下［图8（d）］的局部放大图，选取了一段包含了连续坡面及平台的地形，图上箭头表示为水流流速方向。结果表明，在河道中出渗和入渗呈交替分布。出渗区域位于陡峭坡面处，由于地势相对较高，其总水头较高，土壤中的水容易排出，从而流速较大；而在地势平缓处，水流汇聚，使得这些区域水流由于水头影响更容易产生入渗。这种土壤水分运动规律也符合山区河流中常见的典型阶梯式深潭系统。因此，随着Kr的增大，坡面土壤中的水分会出渗到河道中，使得河道中的流量增大。这也进一步证实了前文对于图6的解释，即Kr较大时主河道水深较高。

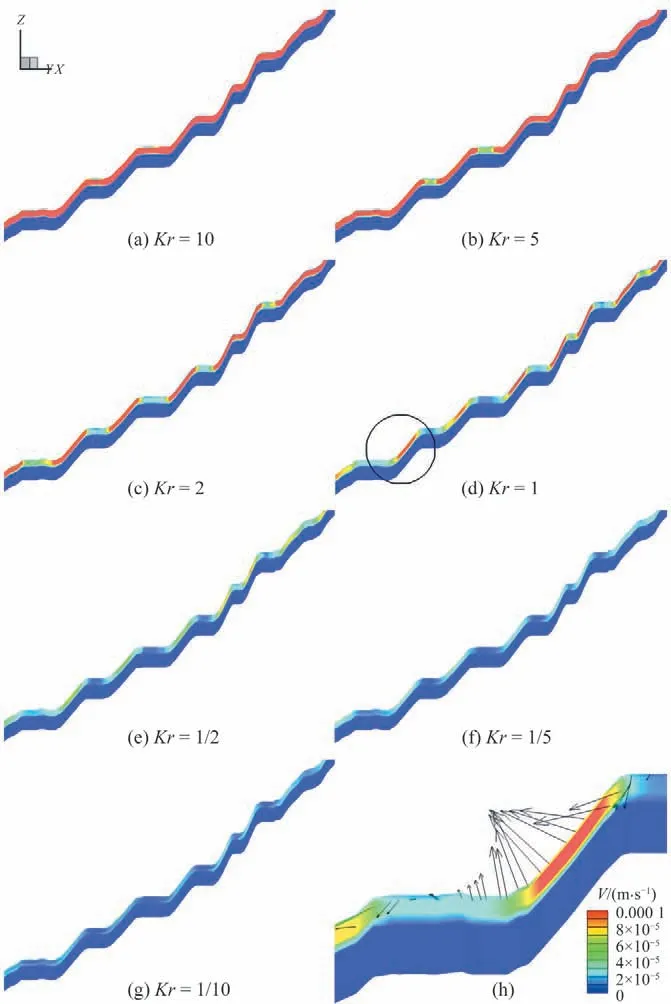
图8 主河道BB′纵剖面流速示意图Fig.8 Longitudinal profile of flow velocity along the stream channel BB′under different Kr scenarios

5 结 论

土壤渗透系数各向异性在自然界中普遍存在，但其在数值模拟中往往被简化为各向同性情形。本文将基于物理概念的分布式水文模型（InHM）应用于中国西南部山区流域，研究了渗透系数各向异性对降雨产汇流过程造成的影响。

结果表明，土壤透水碎石层的渗透系数各向异性对研究区域的产汇流过程有较大的影响。洪峰流量和峰现时间均随Kr而变化，当Kr为10 时，峰值流量比各向同性工况下高出约70%，峰现时间比Kr=0.1 的工况减少近26 min。随后的模拟进一步表明，这些影响是由土壤水分运动的流速和水流方向变化导致的。随着Kr的增大，流速显著增大，尤其是坡面横向水流运动，更多的土壤水分以地下暴雨径流的形式水平流动，从而促进了降雨自地表下渗。当地下暴雨径流到达河道时，较大的Kr也会加速其出渗，使得流量增加。土壤水分运动速度的提高也是缩短峰现时间的原因。

由此可见，在不考虑各向异性的情况下进行数值模拟可能会严重低估洪涝灾害的危害程度，对峰现时间的预警也不够准确，从而影响疏散调度。因此，土壤渗透系数各向异性的特性不能被忽略，合理考虑各向异性比能够提高山洪模拟的精确度，在山洪暴发危及生命财产安全的山区流域，研究土壤渗透系数各向异性对防洪预警具有重要意义。□