基于编码标记点的高精度运动估计

迟书凯，叶 旋，高 翔，解则晓，陶冬冬

（中国海洋大学 工程学院，山东 青岛 266100）

1 引 言

为实现前景运动的精确估计，本文提出了一种基于编码标记点的高精度运动估计方法。前景运动估计指的是估计动态场景（前景）相对于静态场景（背景）的运动参数，包括三自由度的旋转参数以及三自由度的平移参数。其在智能监控、目标跟踪、姿态估计等领域有着广泛的应用。现有的前景运动估计方法主要包括两类：基于RGB 图像的前景运动估计以及基于RGB-D 图像的前景运动估计。

基于RGB 图像的前景运动估计方法主要有光流法［1-2］、目标跟踪法［3-4］、直接估计法［5-6］等。光流法通过估计帧间光流的方式估计前景运动，当前景运动幅度较大时，会因不满足光流假设导致光流估计的失败；目标跟踪法采用基于视觉的目标跟踪方法对前景目标进行跟踪以估计前景运动，这类方法通常只是给出前景目标的包围盒且估计的是目标在图像上的二维运动；直接估计法基于深度神经网络，通过在二维图像上直接估计前景目标的六自由度位姿参数实现前景运动估计，尽管这类方法可以估计六自由度的前景运动，但是这类基于图像的姿态估计方法通常精度相对较低，通常难以满足前景运动估计的精度要求。

另外，对于基于RGB-D 图像的前景运动估计，Li 等人［7］提出了一种同时重建静态背景与非刚体前景的方法，该方法采用实时实例分割算法“你只看系数”（You Only Look At CoefficienTs，YOLACT）［8］实现前背景分割，然后采用刚体与非刚体迭代最近点（Iterative Closest Point，ICP）算法，实现背景与前景的跟踪。上述方法虽然能够实现前景运动估计，但是由于RGB-D 图像中深度图噪声较大且有效范围较小，难以精确捕捉较大范围的前景三维运动，在一些对精度要求较高的场景（如机器人末端运动精确估计）中应用受限。

由上述分析可知，现有前景运动估计方法存在维度缺失、范围受限、精度不足等问题，在对精度要求较高的大范围六自由度运动（如机械臂拾放、机器人搬运等）进行运动估计时，现有方法难以胜任。对此，本文提出了一种面向上述特定工业应用场景运动估计方法，该方法借助编码标记点实现前景运动的高精度估计。相对于场景本身的纹理特征，编码标记点这类人工标志可以提高测量系统的鲁棒性，在场景结构复杂、纹理缺乏等外界条件下仍可提供较高精度的观测量（图像特征点位置），且几乎不会存在误匹配现象。该方法在测量环境内的前背景中均粘贴编码标记点，所采用的标记点为环状编码标记点，不同的编码标记点均可通过环状编码带确定唯一的身份信息［9］。在此基础上，本文提出了一套基于环状编码标记点的高精度运动估计流程，包括编码标记点的提取与识别、与相机的分组、背景点与相机位姿初始化、前景点与前景运动初始化、全局优化在内的五个步骤，可以同时估计相机位姿以及（前背景）标记点三维坐标，实现了前景运动的全自动、高精度估计。本文将图聚类方法引入编码标记点与相机的分组过程，实现了前景运动的全局最优划分；将广义光束平差方法引入编码标记点坐标与相机位姿的优化过程，实现了前景运动的全局最优估计。

2 方 法

2.1 方法概述

本文提出的基于标记点的高精度运动估计方法的输入为自由拍摄的图像，输出为前景运动（旋转、平移）的估计结果。为区分运动前景与静止背景，在测量场景中粘贴编码标记点，并将位于前景运动目标上与背景静止环境下的编码标记点分别称为前景与背景标记点。该方法主要包括五个部分：1）进行编码标记点的识别与提取，获取图像中各点的中心位置以及码值信息；2）采用基于图聚类的方法，实现编码标记点与相机的分组，即自动区分前景与背景标记点以及不同次前景运动分别对应的相机集合；3）采用增量式从运动恢复结构的方式，对背景点三维坐标以及相机位姿进行初始化；4）根据估计的相机位姿，采用三角测量的方式初始化前景点的三维坐标，并通过图优化的方式初始化前景运动；5）对已估计的前背景点三维坐标、相机位姿、前景运动进行全局优化，以获取前景运动的最终估计结果。该方法的流程图如图1 所示，下文将对上述 五个部分进行具体介绍。

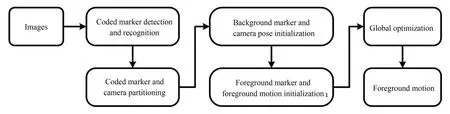
图1 基于编码标记点的前景运动估计方法的流程图Fig.1 Flow chart of the proposed coded marker-based foreground motion estimation method

2.2 编码标记点的提取与识别

在进行编码点的提取时，采用Xie 等人［10］的方法，获取标记点的近似成像中心以及像素级边缘点，并利用Zernike 正交矩［11］实现边缘点的亚像素化。在此基础上，采用随机抽样一致性（Radom Sample Consensus，RANSAC）算 法［12］以 及非线性最小二乘优化，对标记点成像椭圆参数进行初始化与优化。上述优化的目标函数定义如下：

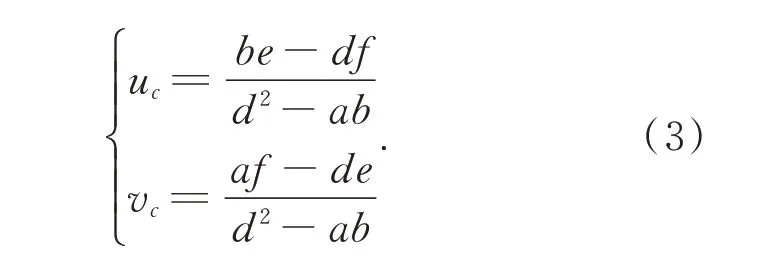
基于编码标记点的提取结果，采用Xie 等人提出的等分椭圆内切圆的方法［9］，获取标记点的码值信息，实现标记点的识别。

2.3 编码标记点与相机的分组

为实现相机位姿以及前景运动的估计，需要先进行编码标记点与相机的分组，即自动区分前景与背景标记点以及不同次前景运动分别对应的相机集合。基于背景标记点数量远小于位于前景标记点的假设，当对一对分属不同次前景运动的图像利用匹配（同一码值）的标记点进行基于RANSAC 的基本矩阵估计［15］时，对应的标记点匹配对内点为背景点，外点为前景点。基于上述观察，可以采用如下的朴素算法进行编码标记点与相机的分组：对输入图像集合中的任意一对图像进行基于RANSAC 的基本矩阵估计并记录其中各匹配对的内外点情况；将各标记点在所有图像对中属于内点的比例作为标记点分组依据，背景点的该比例应高于前景点；将各图像对中匹配标记点的内点比例作为相机分组依据，属于同一次前景运动的图像对该比例应高于分属不同次前景运动的图像对。

然而，上述朴素分组算法存在许多不足：（1）由于共外极线的情况，镜头畸变的存在以及距离阈值的不当，会导致部分内外点的错误归类；（2）对于不同的实验配置，上述算法中内点比例的取值分布会存在区别，因此标记点与相机分组的阈值难以确定；（3）上述算法仅利用了各标记点及各图像对的内点比例这类局部信息，而未利用各标记点之间及各相机之间的全局信息，使得分组算法鲁棒性较差。

针对上述问题，本文提出了一种基于图聚类（Graph Clustering）的自动编码标记点与相机的分组算法，从图论的角度对该分组问题进行建模，将每幅图像及每个标记点分别作为顶点，建立相机图结构及标记点图结构，再通过Dhillon 等人的图聚类算法［16］，实现编码标记点与相机的自动分组，该方法可以有效利用全局信息，有着更强的鲁棒性。在此基础上，对上述加权标记点图进行图聚类，即可实现编码标记点的自动（前背景）分组。

2.4 背景点与相机位姿初始化

经过上一节的编码标记点分组后，可以利用背景点在各幅图像上的投影椭圆中心测量值，借助从运动恢复结构技术［17-18］，估计各背景点的三维坐标以及各相机的位姿（旋转、平移）。由于本文涉及的相机与标记点数量相对较少且标记点的匹配关系精确已知，因此采用一种简化的增量式从运动恢复结构的方法进行背景点与相机位姿的初始化，具体过程简述如下：

Step 1：找到公共可见的编码标记点匹配对数最多的一对图像并根据其匹配标记点成像椭圆中心估计图像对之间的本质矩阵并对其分解获取相对旋转、平移［19］；

Step 2：通过三角测量算法［20］，估计匹配标记点的三维坐标，实现初始图像对重建；

Step 3：通过迭代的形式添加新的图像并进行场景扩展，直至完成所有相机的位姿估计。

在迭代添加相机时，每次选取与当前已获取三维坐标的标记点公共可见对数最多的相机，给定的二维-三维点对应关系，采用基于RANSAC的透视三点（Perspective-3-Point，P3P）算法［21］估计新添加相机的位姿，并采用三角测量算法估计之前未获取的公共可见标记点的三维坐标，实现场景扩展。另外，在初始图像对重建及每次添加图像与扩展场景后，均采用光束平差（Bundle Adjustment，BA）技术［22］对标记点三维坐标，相机内参数及其位姿进行优化。

由于本文中各图像均由同一设备采集，在背景点与相机位姿初始化的过程中各幅图像之间共享内参数。本文采用的相机模型为含有径向及切向畸变的相机模型，相机内参数包括焦距{fx，fy}，主 点p0=(u0，v0)，径 向 畸 变 系 数{k1，k2，k3}，切向畸变系数{p1，p2}。其中，焦距初始值从相机的可交换图像文件格式（Exchangeable Image file Format，EXIF）读取，主点与畸变系数的初始值分别置为图像中心与0，在对相机内参进行优化时固定主点，只优化焦距与畸变参数。根据采用的上述相机模型，若某椭圆实际成像中心为pc=(uc，vc)T，则其理想成像中心p˜c=(u˜c，v˜c)T可通过下式进行计算：

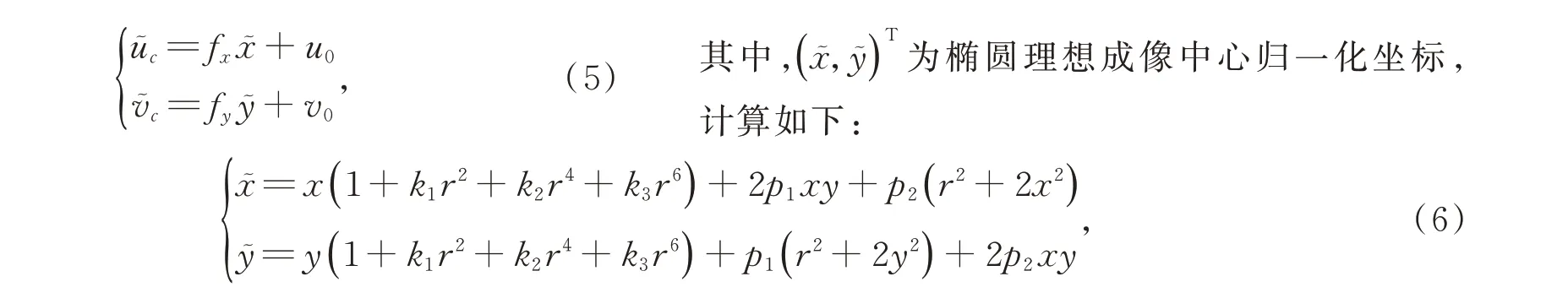
其中，r2=x2＋y2，(x，y)T为椭圆实际成像中心归一化坐标，计算如下：

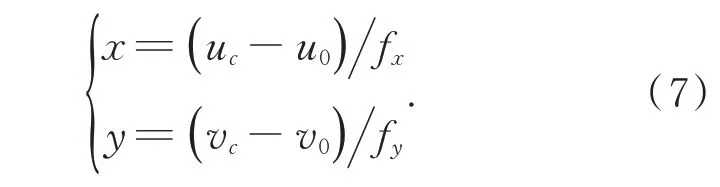
经过上述流程，可以估计各背景点的三维坐标以及各相机的旋转、平移，实现背景点与相机位姿初始化。

2.5 前景点与前景运动初始化

在估计各相机位姿以后，可以通过三角测量算法计算各前景点在不同次前景运动中分别的三维坐标，进而通过各前景点在不同次前景运动中的坐标变换关系表征各次前景运动。需要注意，在对前景点进行三角测量时需要按照相机分组结果，对每次前景运动分别进行。在此基础上，可以通过Arun 等人［23］提出的方法估计各次前景运动之间的相对旋转、平移，并将其记为{Ri，j，ti，j}，其 中Ri，j与ti，j分 别 表 示 第i次 与 第j次前景运动之间的相对旋转与相对平移。然后，根据获取的前景运动的相对旋转与平移构建位姿图，图中顶点表示各次前景运动的绝对位姿，边表示两次前景运动之间的相对位姿。给定位姿图中的相对位姿，采用位姿图优化［24］的方式，估计各次前景运动的绝对位姿初始值，实现前景运动的初始化。上述位姿图优化的目标函数定义如下：

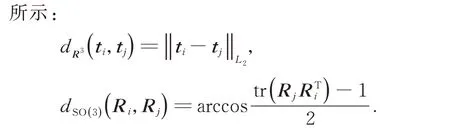
2.6 全局优化

经上述步骤，本文对相机位姿、（前背景）标记点三维坐标以及前景运动进行了初始化，此小节需要利用上述初值，通过非线性最小二乘优化的方式，对上述变量进行全局优化，以实现前景运动的高精度估计。

在此基础上，即可通过求解下式中的最优化问题实现上述参数的全局优化：别介绍上述四类误差项的定义：

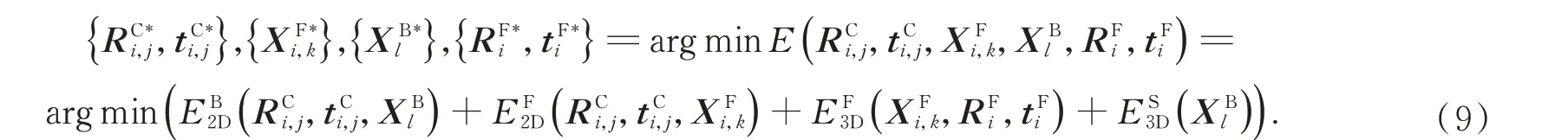
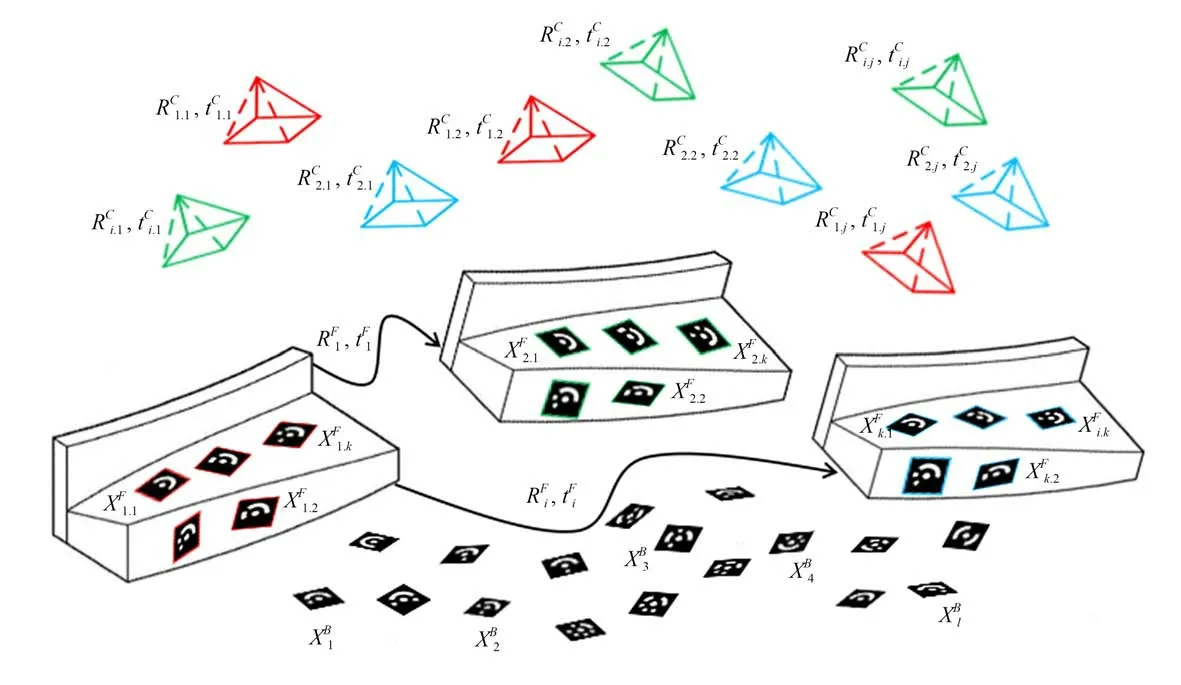
图2 本文前景运动估计系统及符号标记示意图Fig.2 Schematic diagram of our proposed foreground motion estimation system and symbolic representation

基于上述介绍，采用Gao 等人提出的广义光束平差方法［25］，对式（5）进行优化求解，同时最小化其中的反投影误差以及空间误差，以获取前景运动的最终估计结果{RF*i，tF*i}。

3 实验结果

为验证本文提出的基于编码标记点的前景运动估计方法的有效性，现对其中的一个关键步骤编码标记点与相机分组，以及前景运动估计的最终结果进行实验验证。本文采用的图像采集设备为Apple iPhone 7，镜头焦距为4 mm，采集的图像分辨率为4 032×3 024。

3.1 编码标记点与相机分组实验

为验证本文提出的编码标记点与相机分组方法的有效性，将本文方法与2.3 节介绍的朴素分组方法进行对比。在进行对比时，为评价分组效果，需要先确定评价指标。在此，本文采用F1-Measure 进行分组效果评价。具体来说，假设将人工标记的分组结果（真值）与某待评测方法的分 组 结 果 分 别 记 为{Pj|j=1，2，…，N} 与{Ci|i=1，2，…，M}，其中，Pj与Ci分别表示人工标记的分组结果的第j组与待评测方法的分组结果的第i组元素集合。首先，先根据{Pj}与{Ci}计算F1-Measure 矩阵：

对于本文分组方法与朴素分组方法来说，给定不同的基本矩阵估计外点阈值，可获得不同的分组结果。根据上述分组评价指标，即可对两种方法进行分组效果对比，结果如图3 所示。

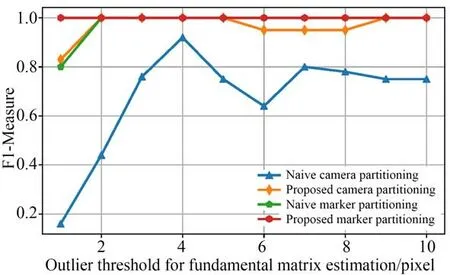
图3 编码标记点与相机分组对比实验结果Fig.3 Comparative results on coded marker and camera partitioning

由图可知，对于标记点分组，两种方法效果接近其都较为准确，而对于相机分组而言，本文提出的基于图聚类的分组方法效果明显优于朴素分组方法。另外，随着基本矩阵估计的外点阈值的变化，本文提出的相机分组方法效果变化不明显而朴素分组方法效果变化剧烈，说明本文方法对外点阈值变化更加不敏感，鲁棒性更强。在实际测量过程中，用于基于RANSAC 的基本矩阵估计的外点阈值取为4 像素。

3.2 前景运动估计精度对比实验

图4 前景运动估计精度评价实验示例图像Fig.4 Example images of foreground motion estimation accuracy evaluation experiment

基于上述评价指标与实验数据，我们首先验证了本文提出的基于RANSAC 与Polar-N-Direction 距离的标记点成像椭圆拟合方法的有效性。具体来说，我们将采用此方法拟合椭圆与基于最小二乘拟合椭圆［9-10］分别得到的椭圆成像中心坐标用于进行前景运动估计，通过比较最终前景运动估计的精度来衡量椭圆拟合的效果，结果如表1 所示。由表1 可知，采用本文方法进行椭圆拟合获取的椭圆中心精度高于基于最小二乘的椭圆拟合方式，能够实现更为精确的前景运动估计。

表1 标记点提取精度对比实验结果Tab.1 Comparative experiment results on coded maker extraction accuracy （mm）

另外，为验证本文采用的相机模型（见2.4节）的有效性，基于上述评价指标与实验数据，进行了优化不同内参数时前景运动估计精度对比实验，结果如表2 所示。由表2 可知，本文采用的相机模型（固定主点，优化焦距、畸变）精度最高，对切向畸变系数以及主点坐标进行优化可以分别提升及降低前景运动估计精度。因此，对于本文选用的图像采集设备及其采集的具体测试数据，我们最终选择优化的相机内参为包括焦距，径向、切向畸变在内的七参数模型：{fx，fy，k1，k2，k3，p1，p2}。

表2 内参优化对比实验结果Tab.2 Comparative experiment results on optimized intrinsic parameters （mm）

为验证本文提出的前景运动估计方法的有效性，基于上述评价指标与实验数据，在此进行了前景运动估计精度对比实现，将本文方法（proposed method）与（1）无全局优化的前景运动估计方法（W/O Global Optimization），（2）朴素的前景运动估计方法（Naive Method），（3）以及基于场景本身纹理特征的前景运动估计方法（Texture-Based Method）进行对比。对于无全局优化方法，直接将2.5 节通过图优化获取的前景运动初值作为前景运动的最终估计结果。对于该朴素方法，在采用本文2.3 节提出的方法对标记点与相机进行自动分组之后，对于同属一组的相机而言，所有标记点均可看作背景点，因此可以采用本文2.4 节的方法计算各组内部的相机位姿与标记点坐标，然后根据各组计算得到的实际背景点的坐标将各组测量结果统一至同一基准之下，在此基础上实现前景运动估计。对于基于纹理的方法，我们将采集的图像导入至当前最具代表性的基于图像纹理特征的三维建模系统COLMAP 中，获取测试场景的稠密点云，结果如图5 所示。由图5 可知，背景固定场景以及4 次前景运动场景均可成功重建。在此基础上先根据标尺将进行场景尺度恢复，然后人为划分出不同次前景运动对应的三维点云并采用带颜色的ICP 算法［26］估计各次前景运动。

图5 测试场景COLMAP 稠密重建结果Fig.5 Dense reconstruction result on the test scene by COLMAP

本文方法与两种对比方法的对比实验结果如表3 所示。由表3 可知，相对于基于图优化的前景运动初始化结果，基于广义光束平差的全局优化能够获得更为精确的前景运动估计，且本文提出的前景运动估计方法在精度与稳定性方面均高于朴素方法与基于纹理的方法，估计误差的均值小于0.3 mm，可以满足大多数场景的测量精度要求。

表3 前景运动估计精度对比实验结果Tab.3 Comparative experiment results on foreground motion estimation accuracy （mm）

4 结 论

本文提出了一种基于编码标记点的高精度运动估计方法。该方法通过在测量环境中前背景上粘贴环状编码标记点，并在每次前景运动后采集若干图像，之后同时估计所有相机位姿以及背景固定标记点、前景运动标记点空间坐标，实现前景运动的高精度估计。针对上述目标，提出了一套高精度运动估计流程，包括编码标记点的提取与识别、编码标记点与相机的分组、背景点与相机位姿初始化、前景点与前景运动初始化、全局优化五个步骤。实验结果表明，本文提出的运动估计方法精度在0.3 mm 左右，可以满足高精度前景运动估计的需求。另外，本文通过实验验证了提出的编码标记点与相机的分组方法以及运动估计整体流程的有效性。