胃肠道机器人的无线能量传输系统的优化

费 倩，王志武*，颜国正，庄浩宇，付文浩

（1. 上海交通大学 电子信息与电气工程学院，上海 200240；2. 上海交通大学 医疗机器人研究院，上海 200240）

1 引 言

随着技术的发展，胃肠道诊疗装置逐渐向智能化、小型化、功能多样化方向发展，目前的最新研究是胃肠道微型机器人，亟需安全、高效、稳定的供能技术支持。电池的寿命短和成本高限制了电池供电设备的发展，所以无线能量传输（Wireless Power Transfer，WPT）技术吸引了越来越多的关注，以规避当前的技术瓶颈［1］。同时，WPT 技术也为胃肠道机器人在人体内连续运动提供了解决方案，同时也能进一步解决生物安全性和供能持久性的问题［2］。

无线能量传输系统是一种很有前途的电能传输技术。但是，如果其系统参数设计不合理，输出功率和传输效率会很低。因此，WPT 的参数优化设计具有重要的研究价值，很多专家学者在这一方面做出了研究。文献［3］在建立的数学模型和差分进化算法的基础上，模拟了输出功率和传输效率随参数的变化，在约束条件下，通过搜索三个参数的最优值来实现效率的最大化。该方法比传统的试错法更有效、更准确，更适合实际的WPT 系统设计。文献［4］采用粒子群优化算法和Pareto 前沿技术，进行感应耦合输电系统的多变量优化设计。通过对常见补偿结构的仿真，对所提出的方法进行了测试。文献［5］提出了一种基于电路仿真的耦合器优化方法，并进一步优化了二次补偿电容以提高系统性能。文献［6］提出了一个用于车载无线供能系统的优化程序，优化的WPT 系统可通过控制功率逆变器的电压向具有变化的充电状态的电池负载供电。文献［7］采用混合差分进化算法对胶囊内镜机器人的WPT 系统进行优化。这些文献都针对WPT 系统在参数或电路设计方面进行了一定优化，但是由于胃肠道机器人工作环境的特殊性，这些方法考虑的因素不全面，并不能完全适用于胃肠道机器人的无线供能系统。

本文通过理论分析构建了胃肠道机器人中WPT 系统的数学模型，找出影响能量传输效率和输出功率的系统参数。为了综合考虑发射线圈和接收线圈各参数对系统的影响，进一步扩展目标函数，然后采用了基于布谷鸟搜索策略的改进粒子群算法来对系统参数进行优化，从而在同时满足传输效率和输出功率的情况下寻求系统参数的最优值，并对优化后的系统进行实验验证。

2 胃肠道机器人无线能量传输系统

本文采用基于电磁感应的无线能量传输系统，其中主要包含能量发射端、能量接收端和负载，系统整体框图如图1 所示。无线传输的基本过程可以描述为：直流电源经驱动电路产生交流电，发射线圈在高频交流电的激励下产生频率相同的交变磁场，接收线圈在交变磁场中通过电磁感应产生感应电动势，然后通过接收电路将高频交流电转变为平稳的直流电为负载供电。

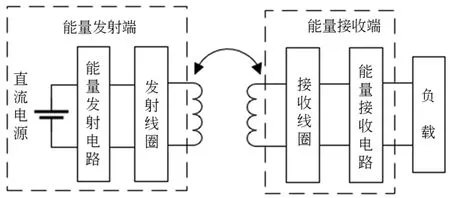
图1 无线能量传输系统框图Fig. 1 Block diagram of WPT system

2.1 模型的建立

根据发射端和接收端补偿方式的不同，无线能量传输系统的谐振补偿模型可分为4 种：发射端与接收端均是串联（SS 型）、发射端串联与接收端并联（SP 型）、发射端并联与接收端串联（PS型）以及发射端与接收端均并联（PP 型）。通过使用反射阻抗理论，可以计算出各种网络拓扑结构的补偿电容［8］。SS 型是唯一独立于耦合系数和负载条件的拓扑结构，因为初级侧的反射电抗等于零［1］。本文的无线供能系统采用SS 型谐振补偿模型，其等效图如图2 所示。图中，发射、接收线圈的电感为L1，L2，绕阻为R1，R2，经过的电流为I1(t)，I2(t)，线圈之间的互感为M，C1，C2为补偿调谐电容，RL为负载电阻，发射电压为Vt，其角频率为ω。根据电路结构，其回路方程表示如式（1）。

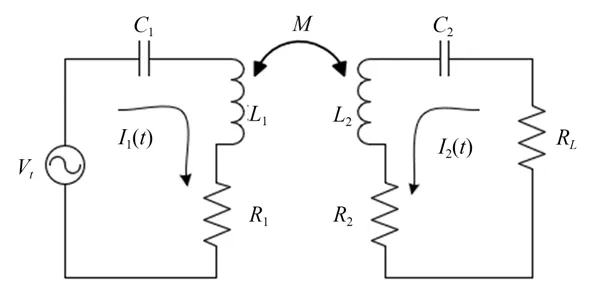
图2 WPT 系统电路模型Fig.2 Circuit model of WPT system

此时，发射端与接收端均处于谐振状态下，传输效率最高。

2.2 发射线圈磁场

对于机器人胶囊无线供能系统来说，发射线圈的位置通常是固定的。因此，发射线圈除了要产生足够的磁场强度外，还需要保证接收线圈在不断运动的过程中接收的能量变化相对平稳，这就需要发射线圈产生的磁场拥有尽可能大的均匀区域。本文用于胃肠道机器人WPT 系统的发射线圈结构，使用方形螺旋式绕制的平板线圈对组合成发射线圈。其相比传统的发射线圈结构，不仅在体积上有所减小，而且线圈结构也更为简单轻薄［9］。

一段载流直导线在空间某点产生磁场［10］为：

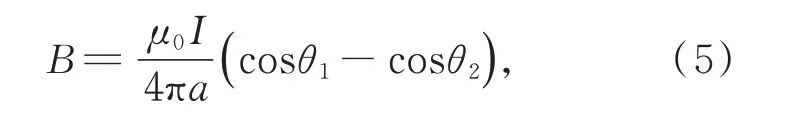
其中：μ0为真空磁导率，I为载流导线内的电流，a为导线长度，θ1，θ2为P 点与导线两端的夹角。

矩形线圈磁场计算示意图如图3 所示，文献［11］由式（5）推出边长2l为的正方形线圈在中心轴线上P 点的磁场为：

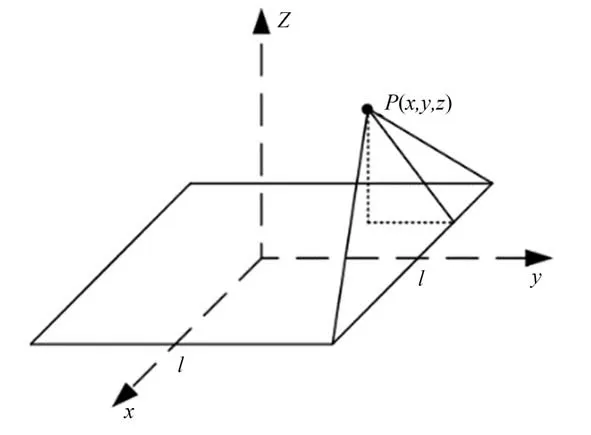
图3 矩形线圈磁场计算示意图Fig.3 Schematic diagram of rectangular coil magnetic field calculation

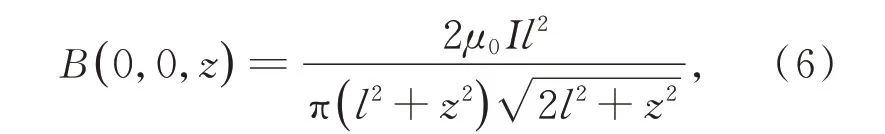
其中：I为载流线圈内的电流，(0，0，z)为P点的坐标。

由于实际的应用过程机器人是不断运动的，分析时无法对每一个位置进行研究，此时应该选取磁场最弱的位置进行研究分析。因此，本文以接收线圈位于平板螺旋线圈中心处进行分析研究。发射线圈是由利兹线从内向外绕制而成，所以每一层线圈的边长都不同，因为是紧密绕制，所以第i层线圈的边长可由式（7）表示：

ai=a0＋2(i－1)d，i=1，2，…，N1， （7）

其中：a0为最内层线圈边长，d为利兹线线径，N1为发射线圈总匝数。

在线圈基板上绕制发射线圈，相对放置，两者轴线相同，两边线圈互相对应，则相距2L的方形螺旋线圈对在中心区域的磁场为：

其中：N2为接收线圈匝数，μr为相对磁导率，S为接收线圈在磁场方向上的等效投影面积。

3 目标函数

3.1 效能积的提出

为了在提高输出功率的基础上同时提高传输效率，文献［12］提出了效能积指标。定义效能积指标（λ）为：λ=效率×目标函数。

该指标综合考虑了系统输出功率、效率等各项指标，在此指标下，同样对系统的互感耦合参数进行分析和优化，从而实现了系统各项指标全局最优。对于不同的系统，其目标函数可能不同。根据实际要求，一个系统其目标可能是输出功率、成本、或者系统工作可靠性等。

在优化的过程中，系统效能积的最大值表示系统具有较大的输出功率和较高的传输效率且两者的关系得到了很好的权衡。同时，记适应度函数为：fitness=1－λ，即在优化过程寻求函数最小值。

3.2 约束条件

由于胃肠道机器人在人体内运动，而且需具备图像采集、诊疗等功能，所以在WPT 系统的设计过程中需要综合考虑多方面因素，包括：生物电磁安全性、温升安全性、最低输出功率、尺寸限制等。

为了减弱高频电流效应的影响，发射线圈和接收线圈均采用多股利兹线绕制。发射线圈使用Φ0.05×1 000、线 径2.5 mm 的 利 兹 线，以500 mm×500 mm 的ABS 平板绕制发射线圈；接收线圈Φ0.07×10、线径0.33 mm 的利兹线，在直径12 mm 的圆筒状磁芯上绕制，尺寸控制在Φ14 mm 范围之内。由于实际应用时人需要躺在发射线圈中间进行检查，所以两线圈间距为500mm。因为功能复杂，胃肠道机器人的所需功耗一般在500 mW 以上［13］，即Pout≥500 mW。

在无线能量传输系统工作时，由于人体内的能量接收线圈存在内阻，电流通过时会使线圈发热，从而对胃肠道组织带来温升安全性问题［14］。根据日本医学电子和生物工程学会（JSMEBE），温度低于42.5 °C 对线圈周围的组织是安全的［15］，这也是保证系统在人体内安全工作的必要条件。从传热平衡角度考虑，即能量接收线圈的发热功率低于散热速率［16］，当满足式（13）时，接收线圈满足散热要求。

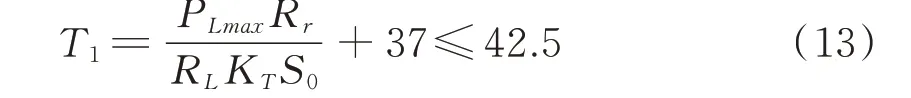
其中：KT为接收线圈散热系数，S0为线圈表面积，Rr为线圈内阻，RL为负载电阻。

因此，整个约束条件为：

式中，磁场强度B由式（2-7）、（2-8）得出，f为谐振频率，N1，N2为发射线圈和接收线圈的匝数，rs为接收线圈半径，R1，R2为发射线圈和接收线圈电阻，RL为负载电阻，μ0为真空磁导率，μr为相对磁导率。其中，rs，N1，N2，f为函数变量。

4 混合粒子群算法优化系统参数

粒子群算法（Particle Swarm Optimization，PSO）是由Kennedy 和Eberhart 共同提出一种群智能优化算法［17］，该算法源于对鸟群捕食行为的研究，具有实现方便、搜索速度快等优点，在解决实际问题中具有一定的优越性。但是，由于PSO是通过不断跟随全局最优解来得到最终结果，所以在遇到有较多局部极小点的搜索空间时，搜索效率可能会大大降低，且不能保证收敛于最优解［18］［19］。针对PSO 存在的问题，本文基于改进的粒子群算法引入了布谷鸟搜索（Cuckoo Search，CS）策略，首先调整了PSO 算法的控制参数，平衡算法的全局探索和局部搜索能力，然后再引入CS 策略，扩大搜索范围，从而提高算法的搜索能力。

4.1 改进粒子群算法（Improved Particle Swarm

Optimization，IPSO）

粒子群算法中，每一次迭代，粒子通过全局历史最优解gbest和个体历史最优解pbest来更新自己的速度，该速度是更新粒子位置的关键，而粒子的位置象征着离最优解的距离。标准粒子群算法的更新公式如下：

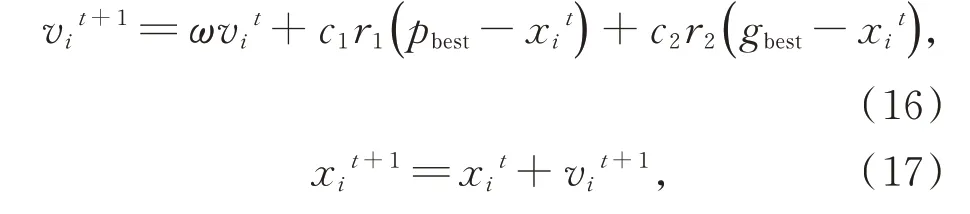
式中：ω 为惯性权重，t代表当前迭代次数，c1，c2为学习因子，r1，r2为［0，1］之间的随机数，用来维持种群的多样性。

由于PSO 算法存在的缺点，已经进行了大量的研究，提出了许多不同的改进策略，调整控制参数就是优化方法之一［20］。本节主要针对学习因子进行了优化，提高PSO 算法的搜索效率。

学习因子c1，c2代表粒子的“自我学习”能力和“社会学习”能力。自我学习因子c1的大小决定粒子向个体历史最优pbest学习的程度，社会学习因子c2决定粒子向全局历史最优gbest学习的程度。因此在迭代初期，c1取值应该较大，使粒子多向pbest学习，增加粒子的全局探索能力，后期则更多向gbest学习，增加局部寻优能力，进而提高整个算法的效率［21-22］。

为了均衡算法的局部与全局搜索能力，提高算法效率，本文利用非线性函数构造学习因子的进化曲线。由于Sigmod 函数在前段和后段变化速度较为缓慢，因此本文选用Sigmod 函数作为构造学习因子调整的基函数。

Sigmod 函数：

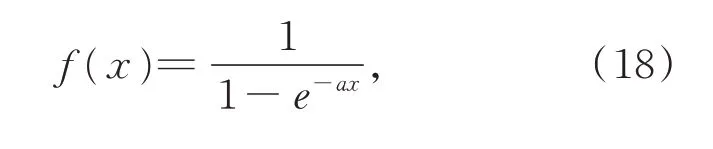
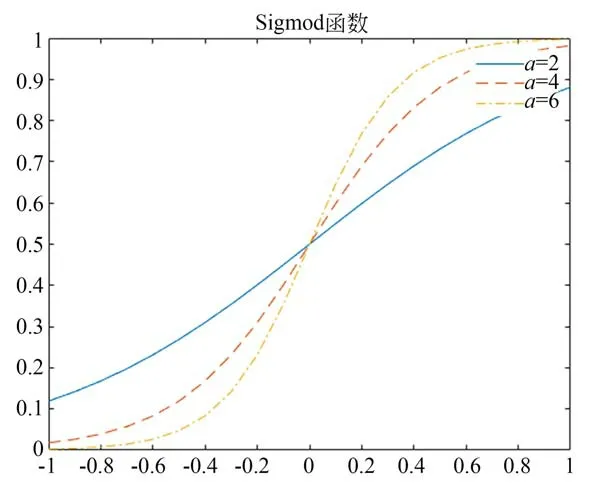
图4 Sigmod 函数曲线Fig.4 Curve of Sigmod function

由上图可知，Sigmod 函数为递增函数，曲线在两端的较小，变化速度较慢；在中间处，曲线斜率较大，变化速度较快。并且系数a 越大，在曲线前段和后段变化越慢，中间变化越快。

根据式（18）设计学习因子的值如下：

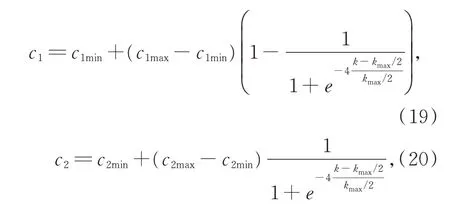
式中：k为当前迭代次数；kmax为最大迭代次数；c1min，c1max，c2min，c2max为学习因子c1，c2的取值范围。由上式可知，c1，c2呈相反的变化趋势。自我学习因子c1随迭代次数的增加而逐渐减少，自我学习能力递减，而社会学习因子c2随迭代次数的增加而逐渐增加，社会学习能力递增。

4.2 布谷鸟搜索策略

布谷鸟搜索（Cuckoo Search，CS）［23］算法，是由剑桥大学Yang 等人提出的一种新型元启发式搜索算法。这是一种基于布谷鸟繁殖行为的算法，集合了布谷鸟巢寄生性和莱维飞行（Levy Flights）模式。布谷鸟通过随机游走的方式搜索得到一个最优的鸟巢来孵化自己的鸟蛋，该算法具有参数少、操作简单、寻优能力强等优点［24］。

定义目标函数f(X)，其中变量X=(x1，…，xD)T，并 随 机 生 成n个 鸟 窝 的 初 始 位 置Xi(i=1，2，…，n)。在得到当前的 最优函数值后，记录上一代最优函数值，并利用式（21）对其他鸟窝的位置和状态进行更新。

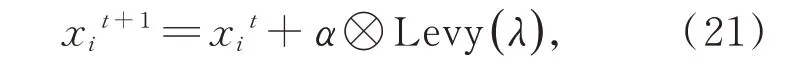
式中，xit表示第i个鸟巢在第t代的位置，⊗表示点对点乘法，α表示步长控制量，Levy(λ)为Levy搜索路径，采用莱维飞行机制，随机步长为Levy分布：

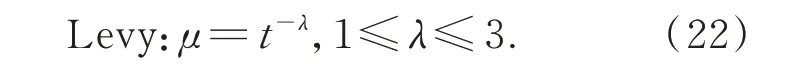
通过位置更新后，用随机数r∈[0，1]与最大发现概率Pa对比，Pa通常取值为0.25，若r＞Pa，则对xt＋1进行随机改变，反之则不变，最后保留最好的一组鸟窝位置yt＋1。

4.3 CS-IPSO 算法的实现

利用CS 算法的优点，将CS 引入IPSO 算法，当搜索到每一次迭代最优解时，不进行下一步而是利用CS 算法继续进行搜索，这样就扩大了原来的搜索范围，从而避免陷入局部最优点［25］。

CS-IPSO 算法的详细步骤如下：

Step1：初始化种群，给定群体规模，空间维度，最大迭代次数，惯性权重和学习因子的范围。

Step2：随机生成粒子的的初始位置和初始速度。

Step3：计算每个位置的适应度，将粒子的位置和适应度存储在pbest、fitness－pbest中，将pbest中的最优适应值的个体存在全局最优gbest和fitness－gbest中。

Step4：根据式（16）、（17）更新种群位置和速度，并对边界进行处理，根据式（19）、（20）更新学习因子；

Step5：计算每个位置的新适应度，并与个体历史最佳适应度比较，更新得到个体最优位置和全局最优位置；

Step6：对个体最优位置进行CS 算法更新：根据式（21）更新最佳位置，随机数r与Pa比较得到新的个体极值；

Step7：个体极值与上次迭代的全局极值比较，得到新的全局极值；

Step8：继续下一次迭代。

Step9：满足停止条件，停止搜索并输出结果。

4.4 结果分析

为了验证优化后的算法的有效性，将CS-IPSO 与IPSO 和PSO 算法进行对比。本文选用如下的4 个测试函数来验证改进后的混合粒子群算法的有效性，测试函数的最小值均为0［26］。

Sphere 单峰函数，主要用于测试优化算法的准确性。Sum Squares 函数是连续的单峰函数，没有局部极小值，可以用来检测算法的收敛能力。Rosenbrock 函数是一个非凸函数，每个等高线大致呈抛物线形，其全域最小值也位在抛物线形的山谷中。很容易找到这个山谷，但由于山谷内的值变化不大，要找到全域的最小值比较困难。Griewank 函数存在许多规律分布的局部极值，可以检测算法跳出局部的能力。

在所有实验中，每个算法中使用的基本参数的值设置为相同的。基本参数设定为：种群维数为10，种群数量为50，最大迭代次数为500。为了减少模拟的随机误差，对每个测试函数的所有实验重复20 次，最终得到的最优值及平均值如表1 所示。为了给出直观和详细的比较，图5-8 给出了几种算法的收敛曲线。Y轴代表基于对数10得到的函数值，X轴代表迭代次数。

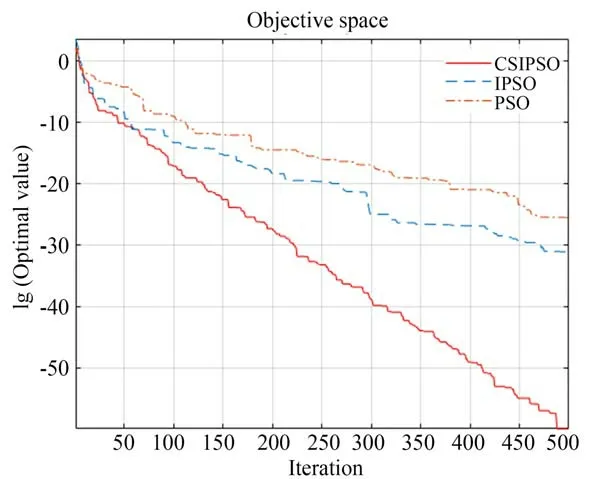
图5 Sphere 函数迭代曲线Fig.5 Iteration curve of Sphere function

表1 测试结果Tab. 1 Test results

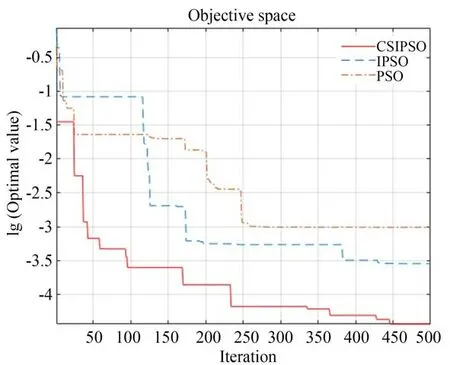
图6 Sum Square 函数进化曲线Fig.6 Iteration curve of Sum Square function

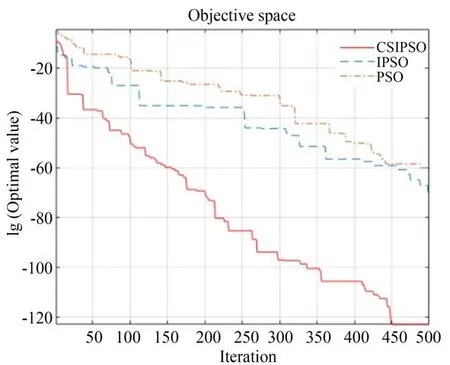
图7 Rosenbrock 函数进化曲线Fig.7 Iteration curve of Rosenbrock function

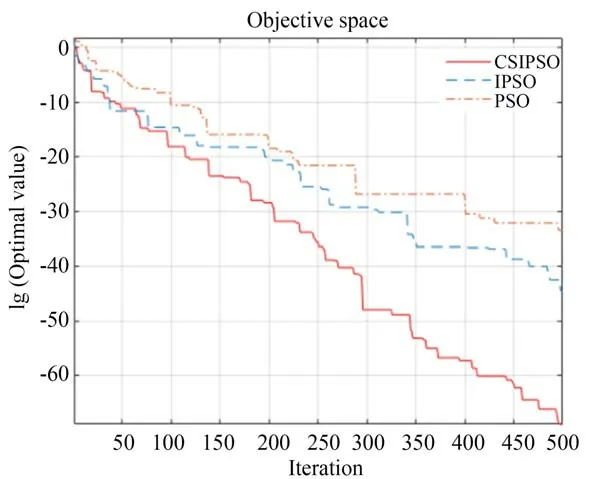
图8 Griewank 函数进化曲线Fig.8 Iteration curve of Griewank function

从上述迭代曲线中可以看出，所提出的粒子群优化算法很快收敛到全局最优，与其他算法相比，CS-IPSO 具有更快的收敛速度。此外，CSIPSO 得到的最优解优于其他算法。通过以上分析和讨论，可以看出所提出的粒子群优化算法对于解决这些基准问题是有效的。改进后的算法在进行搜索的过程中，精度有了明显的提高，收敛的进程也表现出了明显的时间优势。对比其他算法，计算的稳定性也有了很大的加强，在全局搜索能力上也有了提高。

5 实验结果分析

运用优化算法对第3 节中的目标函数式（15）进行优化，4 个变量即为算法的四个维度，根据函数的约束条件确定变量范围。表2 中罗列出了目标函数变量的说明。

表2 目标函数变量说明Tab.2 Description of objective function and variables

目标函数：

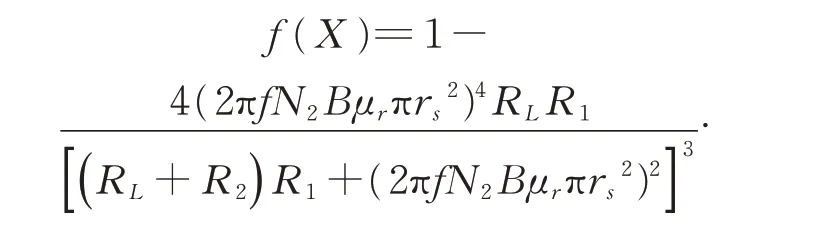
迭代曲线如图9 所示，优化结果如表3所示。

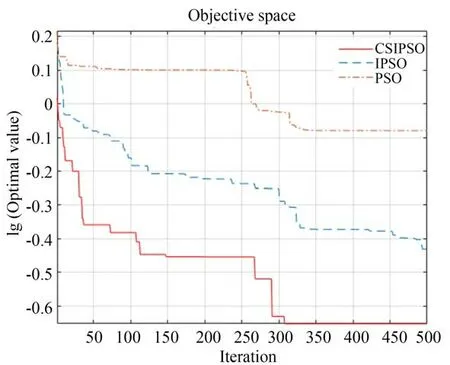
图9 迭代曲线Fig.9 Iteration curve

由图9 可知，CS-IPSO 算法具有收敛速度更快，由表3 可知，CS-IPSO 得出的结果优于另外两种算法，体现了改进算法的优越性。

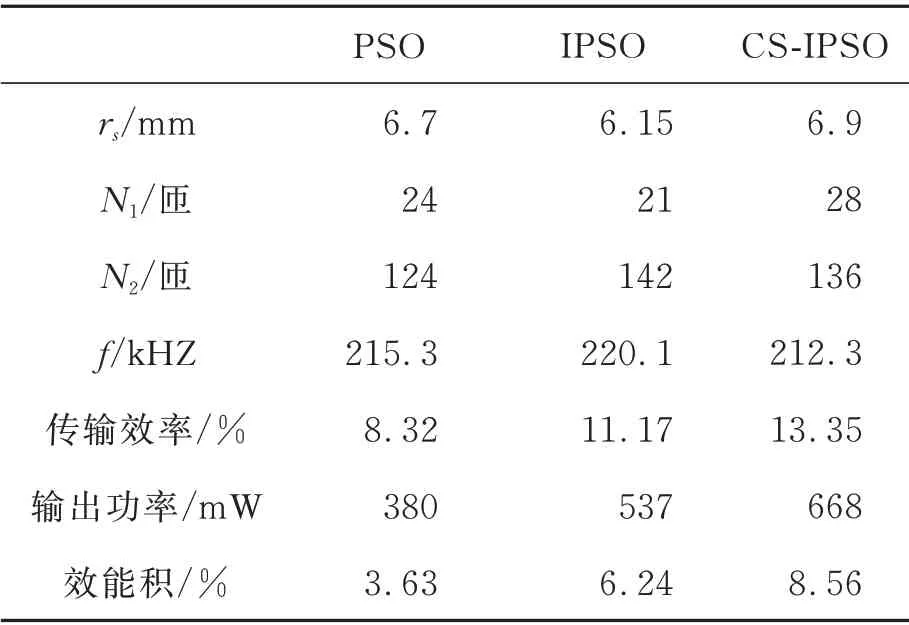
表3 目标函数优化结果Tab.3 Optimization result of objective function

为了验证优化后系统的性能，搭建如图10 所示的实验平台，实验装置的连接如图11 所示。信号发生器产生方波信号以控制半桥驱动芯片，将大功率直流电源输出的15 V 直流电压逆变为峰峰值为30 V 的方波，加载在线圈两端。调节与线圈串联的可调真空电容，通过阻抗分析仪测量，使电路发生谐振。接收端串联阻值为30 Ω 的负载电阻，调节与接收线圈相连的可调电容，使接收线圈与发射线圈在同一频率谐振，此时负载接收电压最大。

图10 WPT 系统实验平台Fig.10 Experiment platform of WPT system

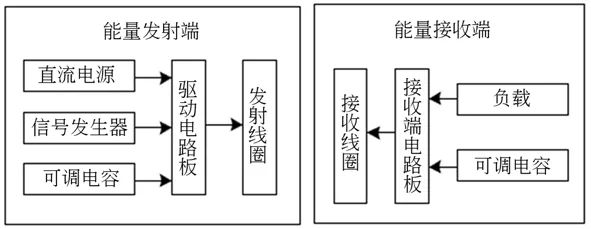
图11 实验装置连接图Fig.11 Diagram of experimental device connection

表4 所示为最终实验结果，可知改进后的系统传输效率为10.12%，输出功率为637 mW，达到预期结果。可以看出，实验结果与算法优化得出的结果差别较大，这是因为理论与实际存在一定的差距。首先，在实际过程中线圈受到高频电流效应的影响，其次由于实验操作的平台是手动控制的，所以在相对位置上存在一定的误差。这些在后续研究中还需要进一步分析与改进。

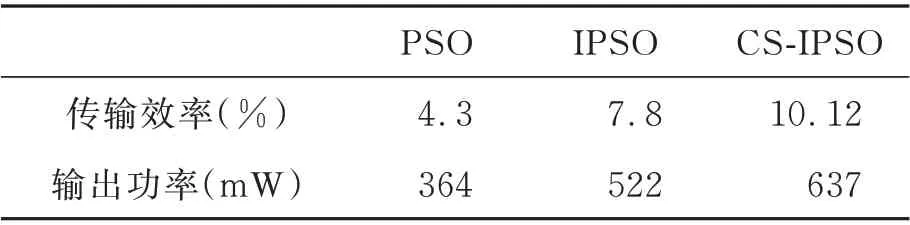
表4 实验结果Tab.4 Experimental results

6 结 论

本文为胃肠道机器人的无线供能系统的参数优化设计了一种基于布谷鸟搜索策略的改进粒子群算法。首先基于平板螺旋发射线圈推导出无线供能系统的数学模型，并采用效能积作为目标函数。然后，在改进的粒子群算法中加入布谷鸟搜索策略。通过测试函数对算法进行比较，显示出本文设计的优化算法的优越性。最后，根据优化后的参数搭建实验平台，进行实验验证，结果为：系统传输效率为10.2%，接收功率为637 mW，实验结果可以达到预期要求。