面向手写数字图像的压缩感知快速分类

肖术明，王绍举*，常 琳，冯汝鹏

（1. 中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2. 中国科学院大学，北京 100039；3. 中国科学院 天基动态快速光学成像技术重点实验室，吉林 长春 130033）

1 引 言

随着计算机技术的不断发展，图像分类算法取得了长足进步，并对人们的生活和社会的发展产生重要的影响。人机交互［1］、天文数据处理［2］、农产品成像［3］以及航空图像处理［4］等领域都离不开图像分类，因此图像分类算法有着重要的研究意义。手写数字图像分类算法指利用计算机图像处理技术将手写数字图像判定为0～9 共10 个类别的过程，该算法在财会、教育和金融等众多领域具有广泛的应用背景和使用价值。

基于神经网络模型的图像分类算法获得了很好的效果，使图像分类算法有了突破性的进展。对于手写数字图像分类问题也涌现了大量的相关研究工作：Hinton 通过构造深层网络模型来学习有效特征的方法，完成了对手写数字集的识别，识别效果优于支持向量机（Support Vector Machine，SVM）。Lee 提出了卷积深度置信网络，此网络能高效的学习和提取自然数字图像的特征。德国的Friedhelm Schweriker 采用SVRBF40 对手写体数字进行识别，测试样本10000个，识别正确率为95.56%［5］。上海交通大学的团队采用压缩子结构特征的方式，用BP 神经网络分类，最终识别率为96.1%，误识率为1.04%。中科院自动化研究所的团队使用有限状态自动机方式对手写数字分类，识别率为95.2%。清华大学的团队利用SVM 技术对邮政纸单上的手写数字做了识别工作，识别率为92%［6］。但是，上述算法都是利用网络模型对手写数字原始的高维数字图像进行图像分类，这极大地增加了网络模型训练计算耗时和最佳训练次数，同时还会影响图像分类的准确率，现有的研究［7-11］也都是对原始的高维数字图像进行处理。

近年来，针对信息量庞大的信号（图像）预处理问题，提出了一种新的信息采集方式，即压缩感知（Compressive Sensing，CS）理论。该理论表明，当信号（图像）具有稀疏性或可压缩性时，通过采集少量的信号（图像）观测值就可以实现信号的准确或近似重构［12］。文献［13］在光学相关断 层 扫 描（Optical Coherence Tomography，OCT）成像技术中引入CS 技术，在压缩感知重构算法中结合分块思想、引入正则项lp范数以及嵌入各项异性平滑算子，该改进的重构算法可以在一定程度上实现频域OCT 图像重构效率和重构质量的平衡。文献［14］中提出了一种基于投影收缩的压缩感知锥束CT 短扫描重建算法，该算法将校正过程引入到压缩感知的图像重建中，有效抑制了条状伪影，清晰重建出边缘细节，极大提高了少量投影数据重建图像的质量。但是，上述的研究都是针对压缩采样信号的重构问题，而对于图像分类问题，可以使用压缩感知技术利用高斯随机矩阵对具有稀疏性的数字图像进行线性观测，少量的信号（图像）观测值保留了全部信息（特征），从而减少后续图像分类的数据处理量。

针对手写数字数据集信息量大，使用神经网络模型对其进行图像分类时训练计算耗时长和最佳训练次数多的问题，引入压缩感知技术，提出了一种基于压缩感知和单隐层前馈网络（Compressive Sensing and Single Hidden Layer Feedforward Network，CS-SHLNet）的手写数字图像快速分类算法。利用高斯随机矩阵对具有稀疏性的手写数字图像进行线性观测，将高维图像信号投影到低维空间得到观测值。将拥有图像全部信息（特征）的观测值嵌入神经网络中对图像进行特征提取。采用神经网络模型对手写数字进行图像分类。实验结果表明，该算法可以有效减少神经网络模型对手写数字数据集的训练计算耗时和最佳训练次数，同时保证分类准确率。

2 手写数字图像快速分类算法

MNIST 是一个手写数字识别领域的标准评测数据集，数据库中有70 000 张灰度图像，毎张图像大小为28×28，即784 维［15］。因此，整个数据集的信息量庞大，传统的手写数字图像分类往往直接利用神经网络对其进行特征提取，训练计算耗时长最佳训练次数多。针对这个问题，利用CS-SHLNet 对手写数字图像快速分类：首先利用压缩感知理论对数据集进行线性观测，得到手写数字的低维空间观测值；然后，将手写数字的观测值作为神经网络模型的输入，利用网络模型进行特征提取；再利用神经网络的学习能力对图像标签之间的相关性进行挖掘，输出最终的图像类别。总体的流程图如图1 所示。

图1 手写数字图像分类流程图Fig.1 Flowchart of handwritten digital image classification

2.1 基于压缩感知的手写数字线性观测

手写数字数据集数据量庞大，为了减少神经网络模型对手写数字数据集的训练计算耗时和最佳训练次数，并且不影响图像分类准确率，利用压缩感知理论对数据集进行线性观测。首先将原始的二维图像列向量化，然后利用观测矩阵对信号线性观测得到观测值。

如图2 所示，MNIST 手写数字数据集数字图片中非零数据数远小于总像素点数图像具有稀疏性，适合利用压缩感知进行图像分析。稀疏度指的是矩阵中非零元素的个数。首先对手写数字数据集图像进行二值化，然后进行稀疏度计算，为了结果的准确性，取所有数据集图像的稀疏度平均值，计算得到稀疏度K。

图2 MNIST 手写数据集数字7 数据特征图Fig.2 MNIST handwritten data set figure 7 data feature diagram

采用一个与稀疏矩阵ψN×N不相关的测量矩阵ΦM×N对信号xN×1进行线性观测，得到M（M＜＜N）维观测值yM×1，即：

其中，ΘM×N为感知矩 阵，yM×1为稀疏信号θN×1在感知矩阵ΘM×N下的线性观测值。

随机高斯矩阵与任何稀疏矩阵都不相关，由约束等距性（Restricted Isometry Property，RIP）条件可知，它可以作为稀疏信号的观测矩阵，并且观测值会保留原始信号（图像）的特征。文献［17］中给出M×N阶测量矩阵ΦM×N的测量边界公式为：

其中：Cδ是一个常数Cδ＜1，K为稀疏度。

由式（3）可知，当N=784 时，可以计算得到M 的取值范围为M≥87.48，本文考虑到后续神经网络数据输入尽量少并且不能丢失图像分类所需特征等问题，选取M=235，可合理实现使用较少的输入数据量，同时保留原始图像特征、保证图像分类准确率。随机高斯矩阵的结构式如下：

MNIST 手写数字数据集中的样本数字5 的线性观测过程如图3 所示。从线性观测的过程图可以看成，采用M=235 的随机高斯矩阵线性观测，数据从784 维减少到235 维，数据量明显减少。

图3 MNIST 手写数字5 的线性观测Fig.3 Measurements of MNIST handwritten number 5

2.2 基于单隐层前馈网络的观测值多标签分类

对手写数字图像线性观测得到观测值后，需要将观测值嵌入神经网络中对图像进行特征提取，因此手写数字图像分类的第二步是建立适应于观测值的神经网络模型。

2.2.1 神经网络模型的构建

基于神经网络模型的图像分类算法中神经网络架构层出不穷，出现了很多复杂的网络结构［18-21］。考虑到网络架构的复杂度和训练耗时的影响，对于手写数字数据集的观测值多标签分类，采用单隐层前馈网络架构。设置神经网络模型为两个全连接层：第一层是1 024 个神经元密集连接的带有ELU 激活的全连接层，第二层是10 个神经元密集连接的带有Softmax 激活的全连接层。神经网络模型结构图如图5 所示。神经网络结构参数如表1 所示。

图4 单隐层前馈神经网络模型结构图Fig.4 Single hidden layer feedforward network model structure diagram

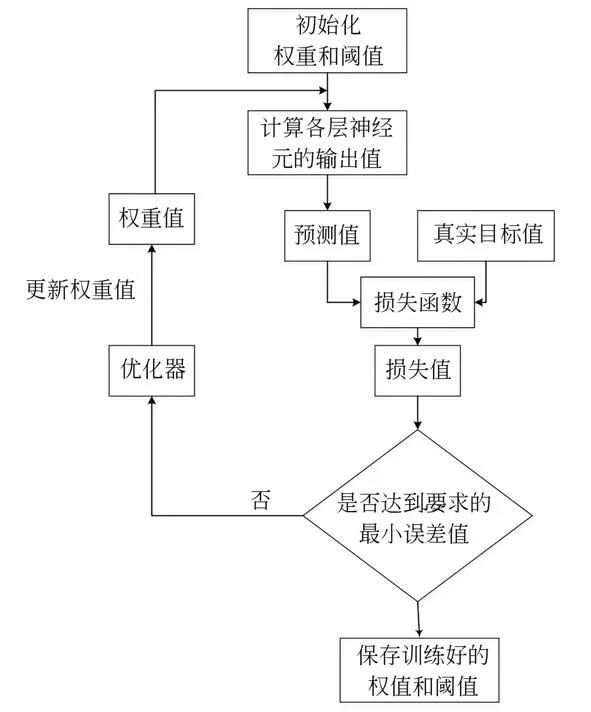
图5 单隐层前馈网络模型权值调整流程图Fig.5 Flow chart of weight adjustment of single hidden layer feedforward network model

表1 单隐层前馈网络结构参数表Tab.1 Neural network structure parameter table

神 经 网 络 的 输 入 为Y=(y1，y2，...，y235)T，y1，y2，...，y235为手写数字的观测值，n为输入层神经元个数。 输入层输出向量为A=(a1，a2，...，a235)T，a1，a2，...，a235为每个输入层神经元的输出值；隐含层输出向量为B=(b1，b2，...，bm)T，b1，b2，...，bm为 每 个 隐 含 层 神 经元的输出值，m为隐含层神经元的个数；输出层输出向量为C=(c1，c2，...，c10)T，c1，c2，...，c10为每个输出层神经元的输出值。输入层到隐含层的权值矩阵为Wm×235，其中ωi，j为权值矩阵的第i行、第j列元素；隐含层到输出层的权值矩阵为G10×m，其 中gp，q为 权 值 矩 阵 的 第p行、第q列元素。

此时，神经网络得到的图像分类标签值就是输出层概率值最高的神经元所对应的分类结果。

2.2.2 神经网络模型的训练

为了调整神经网络的权值，需要根据手写数字训练集的观测值对网络进行训练。如果只将数据标签以0～9 的形式输入模型，会出现不同类别元素之间距离不一的情况，影响分类的准确率，为了保证每个类别的样本彼此独立等距需要对标签进行one-hot 编码。样本标签与one-hot 编码的对应关系，如表2 所示。

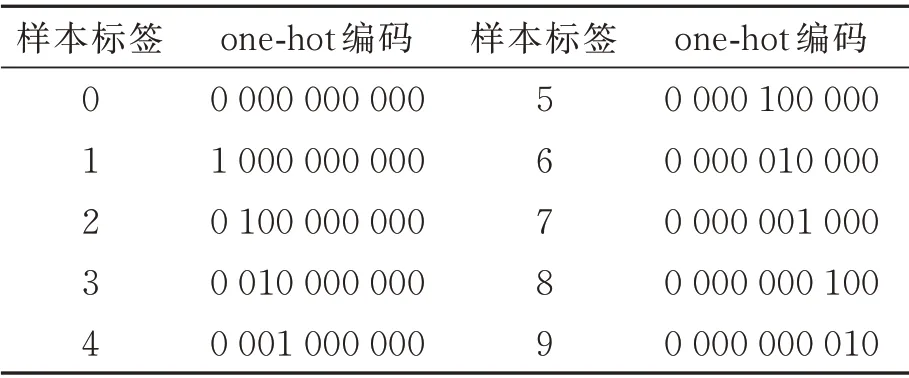
表2 样本标签与one-hot 编码的关系表Tab.2 Table of sample label and one-hot encoding

对于训练样例(y，lab)，lab为训练样例的标签，神经网络的输出为C=(c1，c2，...，c10)T，那么对于手写数字观测值，神经网络模型得到的均方误差为：

当训练误差小于给定误差时，网络模型停止训练，根据式（4）可以得到手写数字图像分类标签值。

3 实验与结果分析

3.1 神经网络模型的构建与训练

通过实验验证神经网络模型对MNIST 手写数字图像分类的快速性和有效性，分析了线性观测值对神经网络模型训练计算耗时、最佳训练次数和分类准确率的影响。

实验环境为Windows 7 64 位操作系统、Intel（R）Core（TM）i7-7700 CPU ＠ 3.60 GHz 处理器、32.0G 内存、显卡NVIDIA GeForce GTX 750Ti 的普通PC 机，编程环境PyCharm Community Edition 2019.1.3 x64，编程语言Python 3.5.2（64 位），使 用TensorFlow_GPU-1.4.0 的Kerase 高级API 构建的一个神经网络模型，来解析图像分类的实现过程。手写数字图像的分类是多分类问题，神经网络模型的损失函数选择分类交叉熵（Categorical Crossentropy），优化器选择rmsprop，指标选择accuracy。

MNIST 数据库中有70 000 张图像，一共包含10 类阿拉伯数字，选择50 000 张图像进行训练，10 000 张进行验证，10 000 张进行测试，MNIST 的毎张图像大小为28×28。图6 列出了本文中使用的部分数据集图像。

图6 MNIST 手写数据集部分样本Fig.6 Partial sample of MNIST handwritten data set

3.2 实验结果分析

为了评估本文算法的性能，将CS-SHLNet与单隐层神经网络、卷积神经网络（Convolutional Neural Networks，CNN）以及深度学习网络做了对比。其中单隐层神经网络的网络结构与本文CS-SHLNet 中的神经网络部分结构相同；CNN 的网络结构主要由3 个卷积层、2 个最大池化层和2 个全连接层组成，卷积核大小为3×3，网络中加人ReLU 激活函数；深度学习网络包括用于字符识别高效的LeNet-5［22］和在ImageNet图像上训练的VGG16［23］预训练模型。实验评价标准为最佳训练次数、训练用时和分类准确率。对手写数字数据集分别通过它们进行训练、验证和测试。

训练集和验证集的性能值（分类交叉熵值）如图7 所示，训练集分类交叉熵值每轮都在降低，这是梯度下降优化的预期结果，但是验证集分类交叉熵值在达到全局最小值后由于过拟合的原因会出现上升的情况。分类交叉熵值达到全局最小值时所对应的轮次为数据集在网络中的最佳训练次数。从图7 中的验证集分类交叉熵值曲线可以得到，手写数字数据集的单隐层神经网络最佳训练次数为5 次，CNN 最佳训练次数为4次，LeNet-5 最佳训练次数为5 次，VGG16 最佳训练次数为13 次；手写数字的CS-SHLNet 最佳训练次数为3 次。

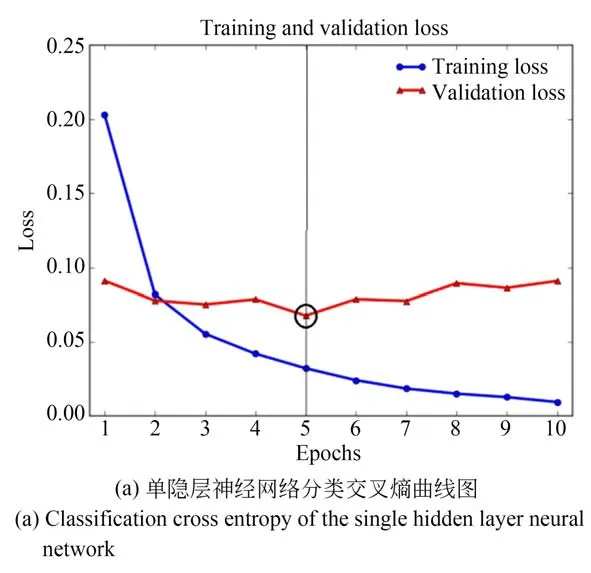
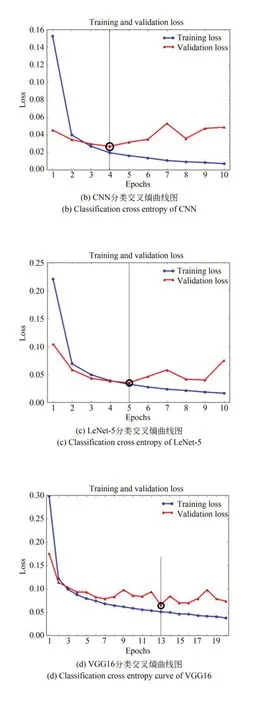
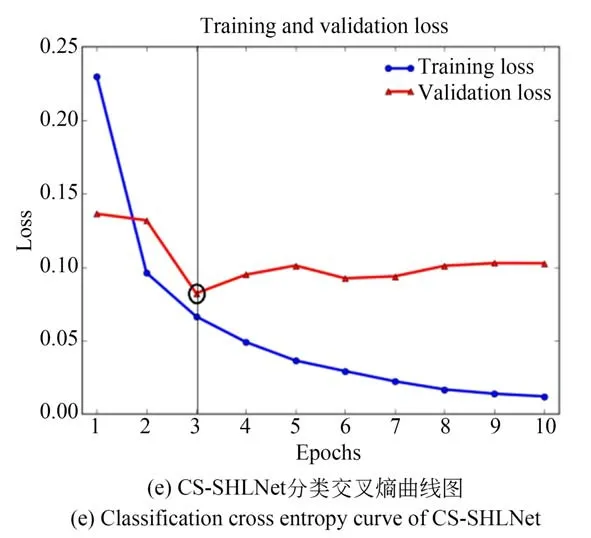
图7 训练集和验证集分类交叉熵曲线图Fig.7 Classification cross-entropy curve diagram of training set and validation set

训练集和测试集的测试精确率如图8 所示，测试集的精确率开始时保持上升趋势，在最佳训练次数时达到最大值。从图8 中的测试集测试精确率曲线可以得到，手写数字数据集的单隐层神经网络最高测试精确率为97.54%，CNN 最高测试精确率为98.83%，LeNet-5 最高测试精确率为98.66%，VGG16 最高测试精确率为97.71%；手写数字的CS-SHLNet 最高测试性能值为97.53%，表明本文提出的算法在减少最佳训练次数、训练时间的情况下，分类准确率基本无影响。

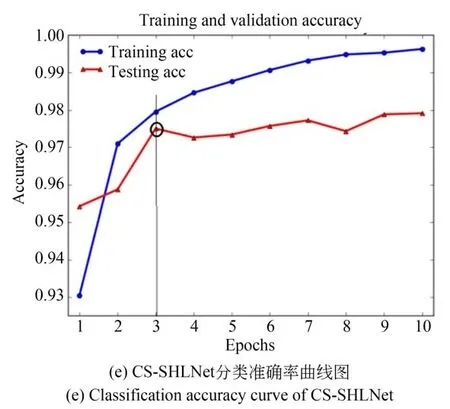
图8 训练集和测试集分类准确率曲线图Fig.8 Classification accuracy curve of training set and test set

表3 为本文CS-SHLNet 方法与其他方法的实验结果对比。从表3 可以看出，网络模型的训练计算耗时缩短为13.05s，最佳训练次数缩短为3 次，分类准确率保持在97.5%。表明该算法可以有效减少神经网络模型对手写数字数据集的训练计算耗时和最佳训练次数，并且不影响分类准确率。

表3 实验结果对比Tab.3 Comparison of experimental results

4 结 论

本文针对手写数字数据集信息量庞大导致神经网络模型对其训练计算耗时长、最佳训练次数多的问题，提出了基于CS-SHLNet 的手写数字图像快速分类算法。通过压缩感知理论，利用高斯随机矩阵对具有稀疏性的手写数字图像进行线性观测，将高维图像信号投影到低维空间得到观测值。通过BP 算法不断调整单隐层前馈网络权值建立适应于观测值的神经网络模型，将观测值嵌入神经网络中对图像进行特征提取。最后，采用单隐层前馈网络模型对手写数字进行图像分类。实验结果表明：相比较单隐层神经网络和深度学习对高维图像（信号）分类，利用CSSHLNet 对MNIST 手写数字数据集进行图像分类，网络模型的训练计算耗时缩短为13.05 s，最佳训练次数缩短为3 次，分类准确率保持97.5%。表明了该算法可以有效减少神经网络模型对手写数字数据集的训练计算耗时和最佳训练次数，同时保证分类准确率。但是该方法是在空域中基于压缩感知理论对手写数字图像进行线性观测，如何进一步减少图像的稀疏度，并且在减少数据量的同时保证特征数据不减少、分类精度进一步提高是下一步的研究重点。