多尺度交替连接残差网络用于图像去模糊

陈清江，胡倩楠，李金阳

（西安建筑科技大学 理学院，陕西 西安 710055）

1 引 言

近年来，图像去模糊技术已应用到医学影像，刑事案件侦破，天文遥感等各个领域［1-2］。图像去模糊技术可以提高图像质量，恢复丢失的信息。因此，研究图像去模糊问题具有重要的应用价值。

图像去模糊任务就是从模糊图像中恢复出相应的清晰图像。去模糊问题一般分为两种，非盲去模糊［3］和盲去模糊［4］。早期研究大多致力于非盲去模糊问题，即模糊核已知，但通常情况下模糊核是未知的，并且盲去模糊［5］是一个不适定问题，这使得盲去模糊任务具有特别大的挑战性。传统盲去模糊方法［6-7］主要利用自然图像的一些先验信息作为正则化项来求解图像去模糊数学模型，迭代估计模糊核进而估计出清晰图像，但传统方法只在特定模糊图像上具有良好的去模糊效果，在其他图像上鲁棒性较差且计算量极大，容易产生振铃现象［8］。近年来，深度学习技术已广泛应用于计算机视觉问题［9-15］，其中包括图像去模糊问题［16-17］。Sun 等［18］用卷积神经网络来去除非均匀模糊，但所用数据集是由清晰图像和模糊核卷积运算所得，与真实模糊图像相差较大，不能很好的恢复真实模糊图像。为此，Nah等［4］提出了一个具有清晰-模糊图像对的逼真数据集—GoPro，并提出一种端到端的多尺度网络去除非均匀运动模糊，获得了较好的实验结果。Tao 等［19］提出了一种多尺度递归网络，利用金字塔形式逐渐恢复出清晰图像，实现更好的去模糊效果，但这些方法仍存在网络模型计算量大，速度慢，高频信息丢失等问题。

受Nah 等［4］和Tao 等［19］的启发，本文提出了一种基于多尺度交替连接残差网络（Multi-Scale Alternating Connection Residual Network，MACR）以端到端的方式去除运动模糊，实现快速恢复模糊图像。本文工作包括以下四点：

（1）本文提出一种基于多尺度交替连接残差网络用于去除非均匀运动模糊，采用“从粗到细”的多尺度网络结构逐渐恢复出清晰图像。本文所提多尺度网络包括两种多尺度：一为输入图像大小的放缩，各个尺度采取相同的网络模型，不同尺度间进行参数共享，降低参数量，防止过拟合现象。二为整个网络特征提取模块采用多尺度残差模块，用大小不同的卷积核来提取不同尺度的特征，然后再进行特征融合。（2）提出一种多尺度残差模块（Multi-Scale Residual Module，MSRM）作为每个尺度的特征提取模块，提高网络模型对每个尺度的适应性、增加网络宽度、提高网络性能。（3）从扩大感受野的角度出发，提出基于扩张卷积的交替连接残差模块（Alternate Connection Residual Block，ACRB）作为整个网络模型的主干，该模块利用带有不同扩张率的卷积层，来增大感受野并提取不同尺度的特征信息。交替连接残差模块与残差密集模块［22］、密集连接模块［23］以及经典的残差模块［24］相比，计算量小且去模糊效果更优。（4）将提出的网络模型在GoPro 数据集［4］上进行训练和测试，并与目前的去模糊算法相比具有更优的去模糊效果。

2 去模糊方法

2.1 交替连接残差网络的构建

本文提出一种基于多尺度交替连接残差网络来进行图像去模糊，如图1 所示。网络采用金字塔模型以“从粗到细”的多尺度结构逐渐恢复出清晰图像，通过多个尺度的输入，让网络学习到不同尺度的特征信息，在不改变网络结构下增大模型的感受野，各个尺度采用相同的网络模型，在每个尺度间改变参数会引入不稳定性［19］，故在各个尺度间进行参数共享，降低参数量和训练难度并使网络更加稳定，采用残差模型来提高网络性能，加快网络收敛速度。整个网络模型由多尺度残差模块（MSRM）和交替连接残差模块（ACRB）堆叠而成。

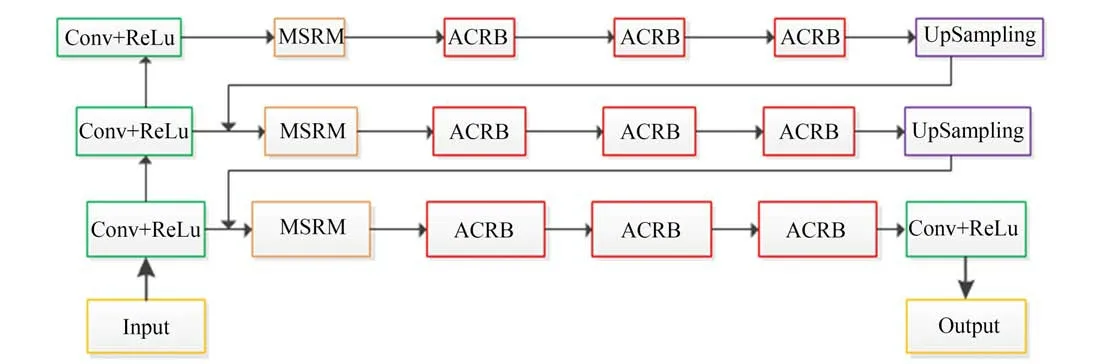
图1 多尺度交替连接残差网络模型Fig.1 Multi-Scale Alternating Connection Residual Network Module

本文所提网络遵循传统方法中的多尺度机制，以3 个不同分辨率的模糊图像Xi(i=1，2，3)作为网络输入，均由原始模糊图像下采样得到，分别为256×256，128×128，64×64。首先，输入最小尺度模糊图像X1进行去模糊处理，得到清晰的潜像Y1，然后再将得到的潜像上采样到与X2相同的尺度，再与模糊图像X2一同输入网络模型得到清晰的潜像Y2，同理，得到最后的清晰图像Y3，这种多尺度网络结构不仅可以恢复模糊图像的整体结构，还能够恢复出图像的纹理细节。各个尺度具有完全相同的网络结构，不同尺度间进行参数共享，降低训练难度，恢复出更加清晰的图像。网络参数配置如表1 所示。

表1 多尺度参数表Tab.1 Multi-scale parameter table

本文利用多尺度残差模块（MSRM）进行特征提取，该模块包括四个分支，如图2 所示。每个分支分别使用1×1，3×3，5×5，7×7 的卷积核来提取具有不同感受野的特征信息，不同尺度的卷积核会产生不同尺寸的感受野，这对于去模糊任务是非常重要的，在四个分支进行特征提取后进行聚合操作（concat）合并，再用一个3×3 的卷积层来融合提取的不同尺度的特征信息，这种信息交互方式能够融合各个尺度之间的特征信息，可以捕获更多的全局信息，使后面的层共享不同尺度的特征信息，最后在输入和输出之间加入跳跃连接来学习残差信息。在此模块中输入输出图像大小均保持不变，每个卷积层后都接一个修正线性单元（Rectified Linear Unit，ReLu），提高网络表达能力。该模块拓展了网络的宽度，获取了更多的特征信息，增加了学习的多样性，提高了网络对尺度的适应性。详细的参数配置如表2 所示。

图2 多尺度残差模块Fig.2 Multi-Scale Residual Module

表2 多尺度残差模块参数配置表Tab.2 Multi-scale residual module parameter configuration table

在图像去模糊任务中，处理严重模糊区域时感受野越大去模糊效果越好，增大感受野的方式有三种：增加网络层数，利用池化层和扩大卷积核大小，但这三种方式会出现增加计算量，重要信息丢失以及梯度消失等问题，而扩张卷积在不扩大卷积核大小的条件下迅速增大感受野，避免了上述问题，故本文利用Yu［20］提出的扩张卷积来增大感受野，提出了一种基于扩张卷积的交替连接模块（ACRB），如图3 所示。

图3 交替连接模块Fig.3 Alternate Connection Module

该模块设计了一种具有成对运算潜力的新型交替连接方式，这种连接方式允许块中的第一个操作与后续任何块中的第二个操作进行交互，这种交互式数量的增加有助于提高图像恢复任务的性能，本文所用的成对操作为卷积层和具有不同扩张率的扩张卷积。由于本文设计了3 个成对操作，共6 层卷积，交替聚合操作（concat）后特征层通道数过多，故引入1 个1×1的卷积用于多通道的特征信息融合，并起到降维的作用。深度网络可以更好的恢复图像，但深度网络很难训练，容易产生梯度消失问题，故此模块利用残差学习来解决网络深度带来的梯度消失问题，提高网络性能。该模块具体参数如表3 所示。

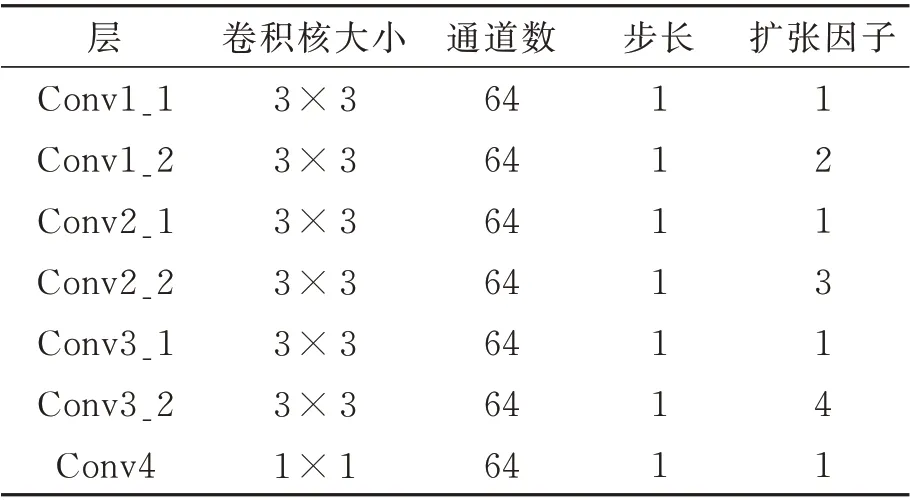
表3 交替连接模块参数表Tab.3 Parameter table of Alternating Connection Module

2.2 损失函数

2.2.1 总损失函数

本文总损失函数由平均绝对误差（Mean Absolute Error，MAE）和结构损失（Structural Loss，SL）组成，其计算公式为：

其中：LA表示平均绝对误差（MAE），LS表示结构损失（SL），λ1，λ2分别为其对应的权重，实验结果表 明：当λ1取0.3，λ2取0.7 时 图 像 去 模 糊 效 果最好。

2.2.2 平均绝对误差（MAE）

均方误差（Mean Squared Error，MSE）或L2损失是目前最广泛的损失函数，然而Lim 等［21］人指出，在峰值信噪比（Peak Signal to Noise Ratio，PSNR）和 结 构 相 似 度（Structural Similarity，SSIM）指标方面，许多使用MAE 损失的图像恢复任务训练取得了比MSE 损失更好的性能。故本文采用简单的MAE 损失作为总损失函数的一部分，计算公式如下：

其中：Ii为真实清晰图像，Iˆi为预测图像。

2.2.3 结构损失（SL）

网络模型在恢复模糊图像时没有约束，容易失去训练方向，导致模型训练不稳定，故引入结构损失作为约束项，增加网络模型的稳定性，提高网络模型的泛化能力。结构损失可以表示如下：

结构相似性定义为：

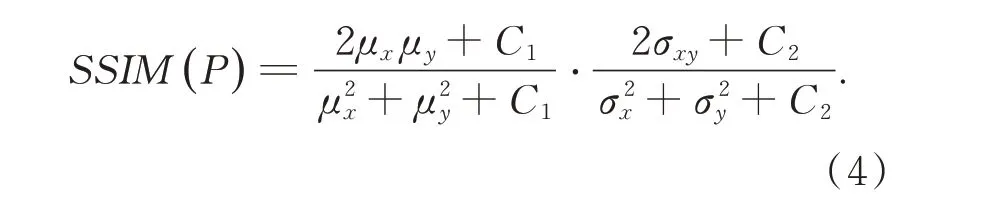
μx，μy分别为图像块像素的平均值，σx，σy分别为图像像素值的标准差，σxy是两个图像像素的协方差，C1，C2为常数。SSIM ∈[0，1]，结构相似程度与SSIM 成正比，SSIM 损失函数考虑了人类视觉感知，LSSIM表示为：

P˜为像素块的中间像素值。

多尺度结构相似度损失（MS-SSIM）基于多层的SSIM 损失函数，考虑了分辨率，LMS－SSIM可以表示为：

P˜为像素块的中间像素值。

3 实验结果与分析

3.1 数据集与实验配置

本实验训练与测试图像来自Nah 等［4］人在2017 年提出的GoPro 数据集，共2013 张清晰-模糊图像对。本文网络模型在此数据集上训练3000 次达到收敛。

实验在Windows10 操作系统下基于Tensor-Flow2.0 深度学习框架与python3.7 进行训练与测试。所用计算机GPU 配置为Nvidia GeForce 1660Ti（6 GB），显存为6 GB。在训练过程中所有输入图像均剪裁为256×256×3，测试时图像大小保持不变，batch_size=2，epoch=3 000。采用Adam 优化器来优化损失函数，动量参数分别为0.9，0.999，实验设置固定学习率为0.000 1。

3.2 实验结果与分析

3.2.1 不同对比算法结果分析

为了验证本文算法的高效性，选取目前最先进的去模糊技术与本文算法进行对比，使用峰值信噪比（PSNR）与结构相似度（SSIM）作为性能衡量标准。表4 为不同去模糊算法在GoPro 测试集上的性能对比结果，图4 为不同网络模型在GoPro 测试集上可视化对比示例图。

表4 不同算法的性能对比Tab.4 Performance comparison of different algorithms

图4 不同算法的可视化对比Fig.4 Visual comparison of different algorithms

从表4 可以看出，本文方法得到了最高的PSNR 和SSIM 值。从图4 中也可以看出Sun等［18］人的算法不能有效的去除图像模糊，Nah等［4］和Tao 等［19］的去模糊效果虽有所提升，但还没有达到最佳效果。运用本文算法所得到的去模糊图像没有明显的伪影，能保持清晰的纹理细节，更接近清晰图像。

3.2.2 多尺度输入结构分析

为了检验多尺度输入结构对图像去模糊任务的有效性，本文分别从主观效果以及客观指标上对比了单尺度，双尺度和三尺度的去模糊效果，均 在Nah［4］等 人 提 出 的GoPro 数 据 集 进 行 训练和测试，各个尺度的性能比较如表5 所示，在测试集上的去模糊效果如图5 所示。

由表5 可以看出，双尺度较单尺度平均峰值信噪比提高了0.842 9 dB，结构相似度提高了0.011 6。三尺度较双尺度峰值信噪比提高了0.756 2 dB，结构相似度提高了0.009 3。从图5可以看出单尺度去模糊效果不好，纹理细节不清楚，双尺度较单尺度去模糊效果有所提升，但布料细节处理效果不佳，三尺度去模糊效果最好，细节较丰富，最接近清晰图像。三个尺度性能最佳，故本文使用三个尺度来进行图像去模糊任务。

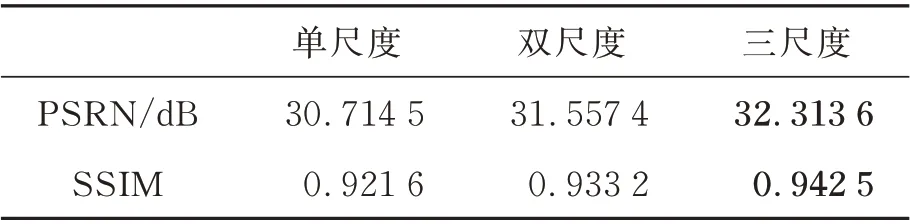
表5 各个尺度性能对比Tab.5 Performance Comparison of each scale

图5 各个尺度去模糊效果对比Fig.5 Comparison of deblurring effects of different scales

3.2.3 交替连接残差模块分析

为了验证本文所提基于扩张卷积的交替连接残差模块（ACRB）对于图像去模糊任务的有效性，分别用残差密集模块（Residual Dense Block，RDB）［22］，密集连接模块（Dense Connection Block，DCB）［23］以及经典的残差模块（Resblock）［24］来代替本文的交替连接残差模块，在相同的实验环境下进行训练与测试，残差密集模块（RDB），密集连接模块（DCB）以及残模块如图6所示，为了快速验证，不同模块对比均在单尺度下进行。

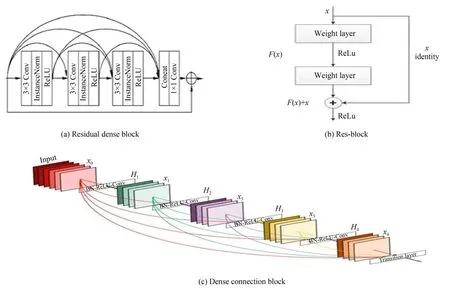
图6 不同模块Fig.6 Different Modules

从表6 可以看出本文所提的交替连接残差模块具有更好的性能，并且从图7 也可看出利用交替连接残差模块恢复的图像细节更丰富，具有更好的去模糊效果。

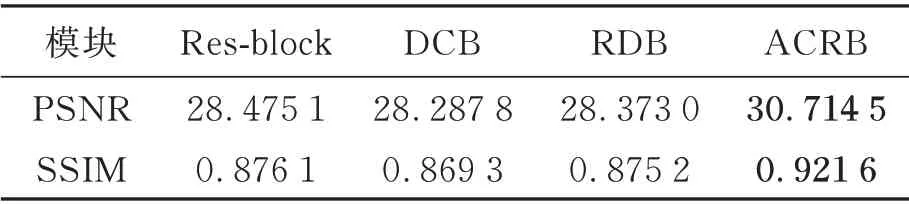
表6 单尺度下不同模块性能对比Tab.6 Performance comparison of different modules in single scale

图7 单尺度下不同模块的主观效果Fig.7 Subjective effects of different modules under single scale

4 结 论

针对目前图像去模糊领域所存在计算量大，恢复图像存在伪影等问题，本文提出了一种基于多尺度交替连接残差网络进行图像盲去模糊，本文仍采用传统多尺度机制，以“从粗到细”的方式逐渐恢复出清晰图像，多尺度输入能减少图像伪影，保持边缘结构。本文提出了一种多尺度残差模块用于提取不同尺度模糊图像的上下文信息。整个网络模型以提出的交替连接残差网络为主干，为图像恢复任务提供更多特征信息，利用平均绝对误差损失和结构损失共同约束训练方向，从而恢复出更加清晰的图像。实验结果表明，本文方法的峰值信噪比为32.313 6 dB，结构相似度为0.942 5，去模糊效果较目前先进的去模糊技术相比有所提升。