基于Radon 变换的空间目标运动方向检测

曹城华，武文波，王 钰

（北京空间机电研究所，北京 100094）

1 引 言

空间目标检测是根据拍摄到的序列星图对太空目标进行搜索定位的过程［1］，是进行空间目标识别、定轨与跟踪的基础，是建立空间态势感知能力的前提。空间目标运动方向和速度估计是空间目标运动特征的一个重要信息，对其进行准确检测具有重要的意义。

空间目标检测算法有多种，可以大致分为两大类：一种是基于星表数据进行星空背景识别，从而将背景分离，空间目标轨迹得以显现。主要弱点是星表中包含大量星等的数据，需要有效提取背景恒星的角度位置等特征信息，并快速检索出其位置。另一种是基于空间目标的运动特征，该方法不需要星表数据，仅利用恒星背景和目标的不同运动模式进行目标检测。程军等人［2］利用背景星图的平移、旋转和比例伸缩不变性和观测星的星等和背景导航星的星等和星对角矩特征进行星图匹配对运动恒星背景空间目标检测。赵臻等人［3］基于星形星图识别算法，利用星对距离和角矩特征进行匹配识别，但模板星图的存储量过大，算法性能有待提高。张劲锋等人［4］基于不变矩和仿射不变矩理论提出组合不变矩的概念，用于空间目标的识别，在不增加目标特征维数的情况下，提高了目标识别的准确率。张晨等人［5］提出使用质心聚焦法，二维直方图统计法和邻域连通法等三种像点簇识别算法进行目标的自动识别。

在空间目标检测检出之后，连续帧图像经过配准，可进一步提取出空间目标的运动轨迹，此外连续帧空间目标的运动方向和速度等信息也可以进一步计算出来。本文采用Radon 变换对检测出的空间目标运动方向信息进一步计算。

Radon 变换在多种图像处理算法中均有应用。范学良等人［6］利用频域分析的方法对水滴运动模糊图像进行处理：利用Fourier 频谱在垂直于水滴运动方向上，有一条高亮条纹，并结合Radon变换识别高亮条纹方向，然后逆时针旋转90 度，计算出水滴运动方向。这给空间目标的运动方向检测提供了一定的借鉴，但没有考虑噪声以及背景对水滴方向识别的影响，也没有考虑多个目标同时运动以及运动轨迹可能为曲线的特殊情况。文献［7-11］基于Radon 变换对运动模糊图像进行运动参数估计。文献［12-13］基于Radon 变换进行人脸识别。文献［14］基于Radon 变换进行多尺度虹膜特征提取与识别。本文在空间目标检测的基础上对空间目标的运动方向特征进行分析计算，采用图像配准，最大值投影，Radon 变换等算法实现对空间目标的运动方向检测。

由于背景进行了配准，因此取各像素坐标位置最大值时，配准后背景恒星保持不变，而空间目标由于和背景的运动特征不同，在配准后的图像上显示出目标的运动轨迹。当对序列帧图像完成所有帧的配准和最大值投影之后，目标的轨迹完全显示出来。最后基于此图像采用Radon变换对空间运动目标运动方向进行检测，进行了各种情况的讨论，并做对比实验验证了该方法在识别空间运动目标方向上的可行性。

2 基本原理与方法

2.1 Radon 变换

Radon 变换［16］用来计算图像矩阵在特定方向上的投影。二维函数的投影是一组线积分，Radon 变换计算一定方向上平行线上的积分，平行线的间隔为1 个像素。Radon 变换可以旋转图像的中心至各种角度，以得到图像在不同方向上的投影积分值。对于一个二维图像f(x，y)来说，其垂直方向上的积分就对应的是在x轴上的投影，同理水平方向上的积分是在y轴上的投影值。

图1 表示任意角度Radon 变换的几何关系。Radon 变换的积分运算过程能够克服噪声对图像产生的影响。从直线检测方面看，Radon 变换空间较之前源图像空间域的信噪比的值更高，故Radon 变换可用于低信噪比图像线检测。空间图像的点目标、低信噪比特征以及空间目标运动特征适合采用该方法。

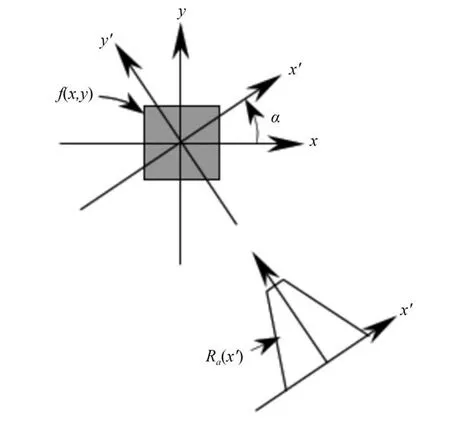
图1 Radon 变换集合关系图Fig.1 Geometrical relationship of Radon transformation

2.2 运动方向检测

在0～180°的区间内，每隔一定度计算一次图像的Radon 变换，以度数为横坐标，取其最大积分值为纵坐标，计算各个角度积分值的均值作为阈值对上图进行分割，获取极大值点对应的横坐标并输出，即为空间目标检测的目标数目和对应目标的运动方向检测结果。实验的整体流程图如图2 所示。

图2 实验流程图Fig.2 Flow chart of the experiment

3 仿真分析

3.1 数据源与预处理

由于真实星空数据稀缺且难以获取，有多种仿真软件可以对星空图像进行模拟，简单的仿真可以随机生成，也可以利用星表数据结合坐标转换关系［17］来生成模拟背景星图。经过对比分析，本文选取Stellarium 天文软件作为实验数据。Stellarium［18］是一款开源的跨平台天象星图模拟仿真软件。可以通过3D 形式展示极其逼真的星空，它的功能强大，默认星表包含超过60 万颗恒星及8 万深空天体，而附加星表包含超超过1.77亿颗恒星及百万深空天体。本文从其官网获取星空图，并以该数据源作为星空背景图像并对空间目标进行仿真实验。

设置Stellarium 星图软件的成像系统参数如下：成像系统指向模式可以为地面观测模式、恒星观测模式或目标观测模式，谱段为全色可见光波段，探测能力为6 等星，视场为2°，生成图像尺寸为1 024×768，帧频根据目标的运动速度动态可调节。首先对获取的星空图像每隔一定时间截取一次序列帧图像。然后对每帧图像进行中值滤波滤除图像噪声，中值滤波是使用邻域中各像素的值进行排序后取中间值作为滤波后对应位置像素值的非线性滤波技术，它的特点是对异常值不敏感，可以在不影响图像对比度的情况下有效地消除孤立噪声点对图像的影响。之后在各个帧背景图像上添加目标点。由于观测平台的运动，导致恒星背景相对相机坐标运动，添加的目标点相对恒星背景运动，采用OTSU 最大类间方差法对包含空间目标的恒星背景图像进行分割，该算法通过计算方差获取合适的灰度值划分图像，能够保证划分开来的两部分内部的灰度值差异最小，而两类之间的灰度值差异最大，由于方差最大，因此错分概率最小。分割之后获取恒星背景和单独的恒星或空间目标亮点。提取并使用质心法［19］计算每帧图像中最亮和次亮的恒星的质心坐标，质心横坐标xc和纵坐标yc计算方法采用公式（3）和（4）以像素为单位进行计算得出。

在连续两帧之间计算对应位置背景恒星坐标，得到序列如表1 所示，其中Δxi=xi＋1－xi，Δyi=yi＋1－yi，单位为像素。可以看出连续帧间的时间间隔恒星背景的运动呈现出匀速直线运动的特征，由于像素个数为整数，因此取均值并取整得——Δx=97，——Δy=69 作为背景的运动特征。通过再次按照相同的计算方法对帧序列图像的次亮点恒星进行计算，验证了该运动特征的准确性，并基于此对序列图像进行配准和最大值投影算法处理。

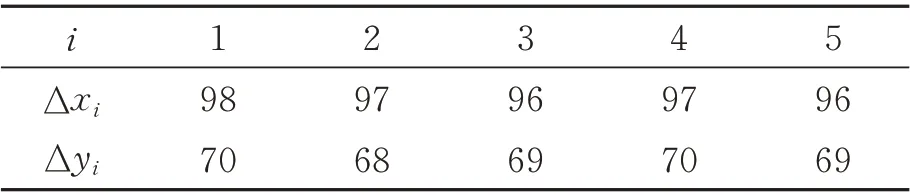
表1 序列帧图像计算运动特征结果Tab.1 Movement characteristic of sequential space image

观测卫星一般有两种工作模式：一种是保持对恒星的观测位置不动，空间目标的运动在多帧图像经过图像配准之后呈现线条状轨迹。另一种模式是长时间曝光模式，由于相对运动，导致恒星和空间目标均呈现出线条状轨迹，但由于空间目标和恒星的相对运动规律的不同，线条方向有所不同，恒星的线条方向保持一致，目标的线条轨迹相对恒星背景在相机视场中具有随机性。

在第一种相机模式中需要进行图像配准，借鉴文献［20］中最大值投影算法及三角形匹配算法思想以及运动参数估计计算恒星背景的沿x轴和y轴到运动参数，并进行最大值投影，得到处理后的图像如图3（a）所示。在第二种模式下得到的图像如图3（b）所示。

图3 模式一（a）和模式二（b）的结果Fig.3 Result image of pattern one and two

3.2 单目标分析

对图3（a）中的空间目标运动轨迹图像进行0～180°区间每隔一度进行一次Radon 变换，并以角度为横坐标，对应角度的积分值作为纵坐标，得到曲线图如图4 所示。可以看出在39 度方向上积分值达到最大，并且明显高于其他方向上的积分值，结合图像上的空间目标估计和负x轴方向的夹角，故准确检测到了一个空间目标的沿39°方向上的运动方向特征。

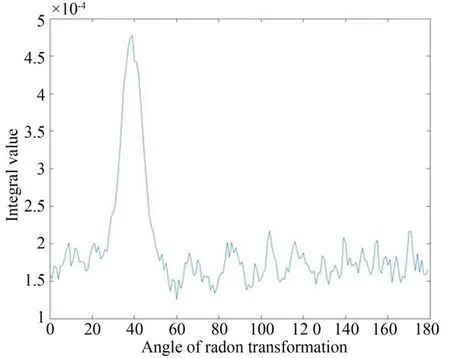
图4 Radon 变换不同角度积分值Fig.4 Integral value in different angles of Radon transformation

3.3 多目标分析

考虑到空间目标运动位置的不确定性，在同一帧序列图像中可能出现多个运动目标，因此需要对多个运动目标同时进行检测。图5 进行Radon 变换沿不同角度积分值图像如图6 所示，可以看出3 个目标分别在39°，90°，144°方向处检测到运动目标。可以看出该算法对多个目标同时进行准确方向检测。

图5 多空间运动目标图像Fig.5 Image of several objects

图6 多目标Radon 变换不同角度积分值Fig.6 Integral value in different angles of Radon transformation

3.4 弧状轨迹分析

由于空间目标的运动轨迹不确定性以及观测相机和目标的相对位置关系不确定性，在同一帧序列图像中运动目标的运动轨迹可能为圆弧状，本节针对圆弧状轨迹的目标进行分析，图7进行Radon 变换沿不同角度积分值图像如图8所示，可以看出Radon 变换后的图像在20～65°之间出现明显的连续亮斑，于是计算出该圆弧的对应的圆心角的弧度为45°，即圆弧状轨迹可以检测出运动方向的范围和圆弧所对应的的圆心角。

图7 圆弧状目标轨迹Fig.7 Image of circular object track

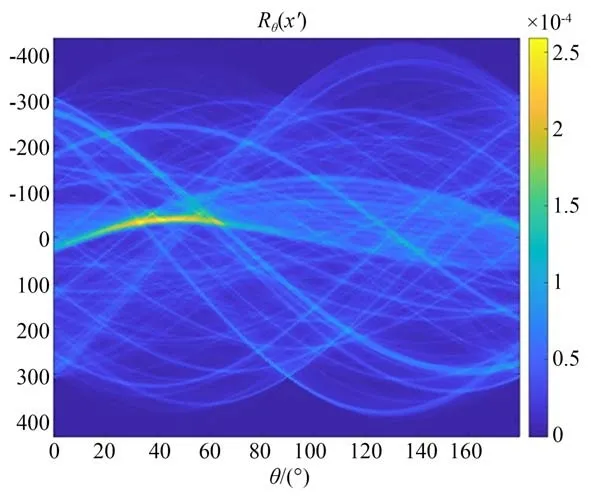
图8 Radon 变换Fig.8 Integral value of Radon transformation

3.5 噪声影响分析

在图3（a）的基础上添加高斯白噪声生成图9，之后对其进行运动方向检测，Radon 变换不同角度积分值结果如图10 所示。由图10 可以看出，添加噪声后对空间目标运动方向的检测基本无影响。但由于噪声的引入，在各个方向上的积分值均会增加。将高斯白噪声的均值分别设置为0.025，0.05，0.075，0.1，0.15，0.2 等不同的值，然后计算运动方向计算的相对误差值，得到曲线如图11 所示，其中第一条曲线为实验结果，第二条为二次拟合得到的曲线。可以看出，当噪声均值小于0.1 时，运动方向检测的相对误差率在5%以内，精度较高；当噪声均值逐渐增大时，误差率随之增大；当噪声为1 时，整个图像充满噪声，空间目标轨迹淹没在噪声中，无法进行检测。

图9 添加噪声Fig.9 Result image after adding noise

图10 Radon 变换不同角度积分值Fig.10 Integral value in different angles of Radon transformation

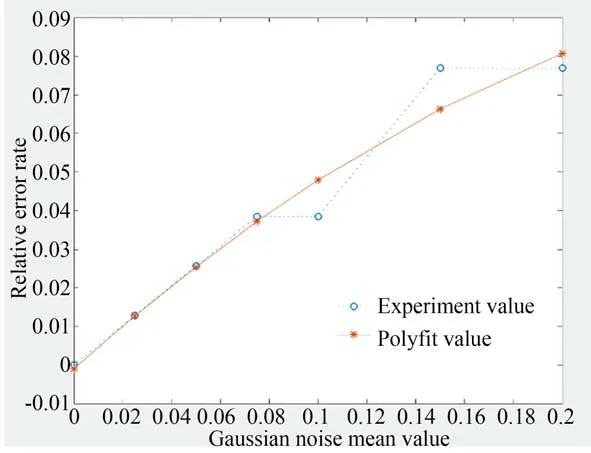
图11 高斯噪声均值对空间目标运动方向相对误差率Fig.11 Relative direction error rate with different gaussian noise mean value

3.6 识别准确性验证

表2 给出了0～180°之间，每隔0.2°计算一次Radon 积分值并取最大值对应的角度作为空间目标运动方向识别结果和实际运动方向绝对误差。本文算法处理流程和文献［6］中算法流程进行对比计算分析可得，本文的绝对误差均值为0.022 2°，文献［6］中为0.722 2°，表明本文提出的算法识别方向的均值更接近目标运动的真实方向。本文的绝对误差方差为1.213 6，标准差为1.101 6。文献［6］中方差为1.741 8，标准差为1.319 8，这表明本文提出的算法的运动方向识别的误差稳定性更好，目标识别的方向误差趋近于更小，精确度更高。

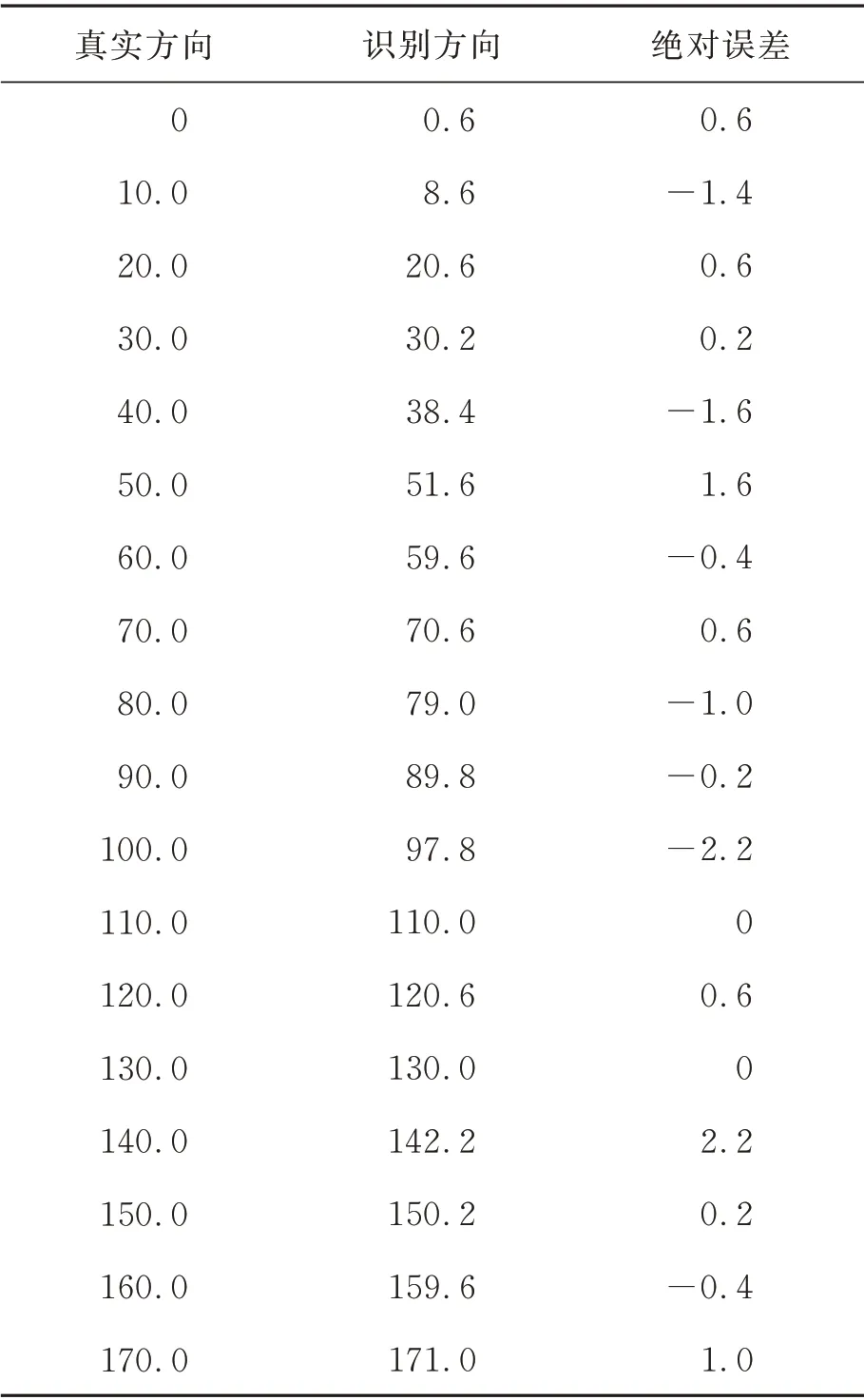
表2 空间目标方向识别结果Tab.2 Movement direction of space target （°）

4 结 论

空间目标序列帧图像经过预处理、图像去噪、图像分割、质心检测、背景运动参数估计、图像配准、最大值投影等处理后，通过设计实验使用Radon 变换对其进行处理分析，可以有效检测出空间目标的运动方向，并且识别的精确度和准确度较参考文献［6］有所提高，能够检测多个运动目标的运动方向，支持对圆弧状运动轨迹进行分析，并对噪声有一定的抗干扰能力，这将对后续空间目标的多维度特征提取、初轨确定、空间环境预警等提供一定的帮助。