超精密全口径抛光机气浮转台的静态特性

安 磊，王 伟*，廖德锋

（1. 电子科技大学 机械与电气工程学院，四川 成都 611731；2. 中国工程物理研究院 激光聚变研究中心，四川 绵阳 621900）

1 引 言

抛光工艺作为一种高面形精度的加工工艺，广泛应用于全口径超精密平面光学元件的加工中［1-2］。与传统的机械接触或液体支承相比，气体静压支撑具有摩擦小、无污染、精度高、寿命长等优点，因而适合应用于超精密全口径抛光机转台。气浮转台利用有压力的气体在基座和转台间形成一层气膜，从而将两者分开，并利用气体静压原理形成承载［3-7］。

国内外学者在静压支撑方面做了大量研究。崔海龙等［8］基于流体力学和固体力学的基本控制方程，建立小孔节流空气静压轴承双向流固耦合数值模拟模型，获取了设计参数对承载力和刚度的影响规律。李一飞等［9］基于fluent 研究了供气小孔尺寸、气腔尺寸、气膜厚度以及供气压力等参数对静压轴承承载力和刚度的影响，为工程设计提供了一定的参考。赵晓龙等［10］采用FDM（有限差分法）和超松弛迭代法对变截面节流器的空气静压轴承模型进行求解，指出变截面节流器的设计方法能够有效提高空气静压轴承的静态 特 性。Belforte 等［11］基 于FDM 分 析 了 不 同 结构的均压腔对支撑表面压力分布、气体流量和刚度的影响。Lo 等［12］和Liu 等［13］基于FDM 分析了静压轴承的压力分布、承载力以及体积流量率等静态特性。文献［14-17］分析了节流器布局、尺寸、形状以及运行参数如供气压力等对静压轴承静态特性的影响。Abdurrahim 等［18］基于FDM 和DTM（微分变换法）分析了不同轴承倾斜下的气膜厚度、压力分布和承载力，Shi 等［19］在此基础上研究了不同转速和转子倾斜下轴承的静态特性。熊万里等［20］和刘志峰等［21］分析了不同倾斜状态下液体静压轴承油膜的承载特性。

可见，以往的研究较多地关注结构参数和气源参数等对气浮支撑的气膜厚度、压力分布、承载力等静态特性的影响，对于角摆和转速的影响也较多的集中于静压和油膜轴承。气浮转台的尺寸和质量较大，工作时转台处于悬浮状态，在制造误差、偏载等因素的影响下会存在倾斜角摆。角摆和转速的存在会导致气膜流场发生变化，从而影响气膜压力分布和承载力，导致转台动态旋转轨迹发生改变，致使超精密光学工件的形状误差，表面质量等出现变化，从而不能达到使用要求。学者在研究气浮转台静态特性时，对于角摆和转速效应的影响关注较少，相关研究并不多见。本文基于柱坐标系下的雷诺方程和流量平衡方程，结合考虑角摆后的气膜厚度方程采用FDM 进行数值求解，研究单个角摆、组合角摆和转速对气膜厚度、气膜压力分布以及承载力这些静态特性的影响。

2 全口径抛光机气浮转台结构与流体润滑分析数学模型

2.1 气浮转台结构

图1 为全口径抛光机气浮转台结构简图，高压气体经节流小孔进入均压腔，进而进入基座和转台间，形成环形气膜，利用静压原理形成承载。

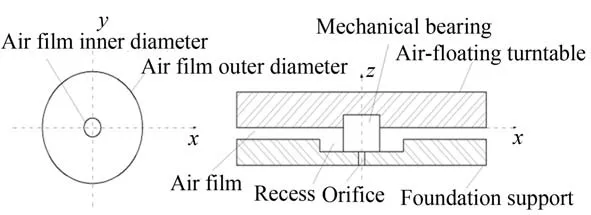
图1 气浮转台结构简图Fig.1 Structure diagram of air-floating turntable

2.2 气膜流动控制方程

转台工作时气膜厚度为微米级别，气体流动为连续介质流动，所以遵循三个基本守恒定律：质量守恒定律（连续性方程）、动量守恒定律（N-S方程）和能量守恒方程（伯努利方程）。其中N-S方程可以描述流体流动的基本规律，但是其作为复杂的偏微分方程很难求解，因此基于一些假设建立连续性方程和简化后的N-S 方程可以得到稳态气膜润滑Reynolds 方程：

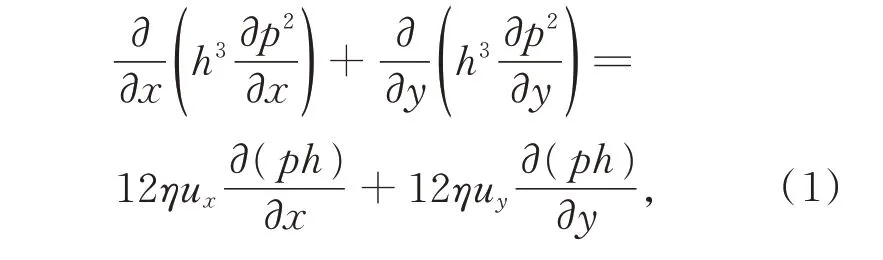
其中：p为气膜压力，η为气体动力粘度，ux为转台在x方向的速度，uy为转台在y方向的速度。

在Reynolds 方程中，h为气膜厚度，当转台存在角摆时：

其中：h0为无角摆时气膜厚度，ϕ为绕y轴的角摆，ψ为绕x轴的角摆。

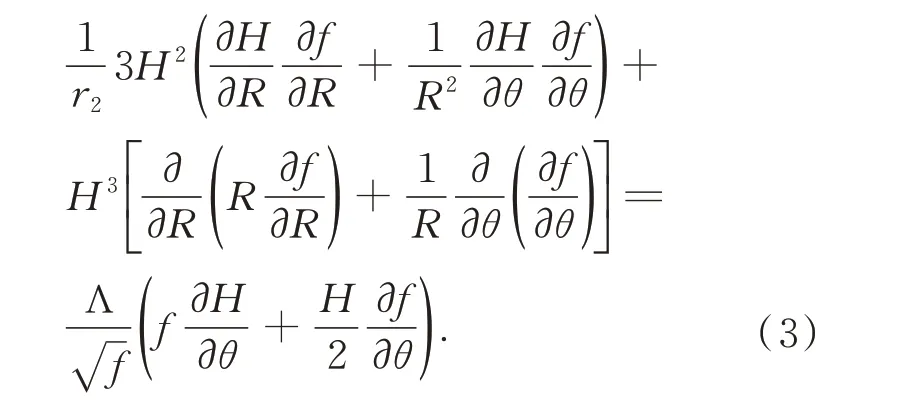
2.3 流量平衡方程

经过节流小孔的入口气体流量为：

其中：A为小孔面积，ps为供气压力，φ为小孔流量系数，一般取0.8，ρa为大气密度，pa为标椎大气压，ϑ为流量函数，k为热容比，一般取1.4，pd为均压腔内气体压力，β为压力比，βk为临界压力比。

出口流量满足下列方程：

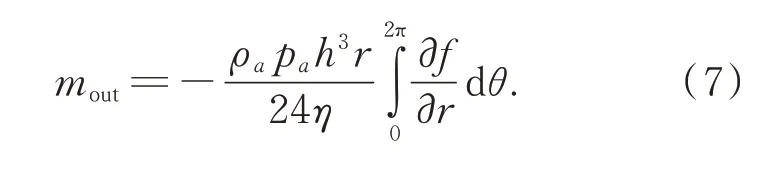
在稳态情况下，入口气体流量应当等于出口气体流量，则流量平衡方程为：

2.4 数值计算

雷诺方程是二阶非线性偏微分方程，其解析解很难获得，通常采用数值求解方法对其离散化得到可求解的代数方程组。常用的离散方法有FDM，FEM（有限单元法），FVM（有限体积法）以及DTM 等，FDM 在求解时计算用时少，编写过程灵活，受到广泛的应用。

如图2 所示，将气膜流场区域在周向和径向分别划分为n份和m份，则周向节点数为n，径向节点数为m＋1。对于边界条件：在与大气相连处，fi，j=1。在均压腔内，fi，j=(pd/pa)2。周期性边界为fi＋n，j=fi，j。

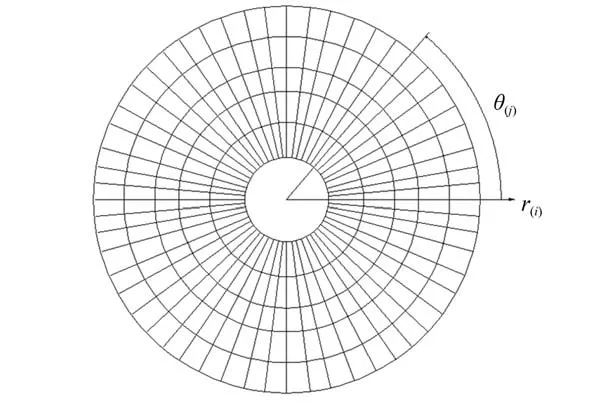
图2 气膜流场数值计算网格模型Fig.2 Numerical calculation grid model of air film flow field

采用五点中心差分将偏微分项进行转化：

将（9）式带入（3）式，则离散后的雷诺方程如下：

其中：

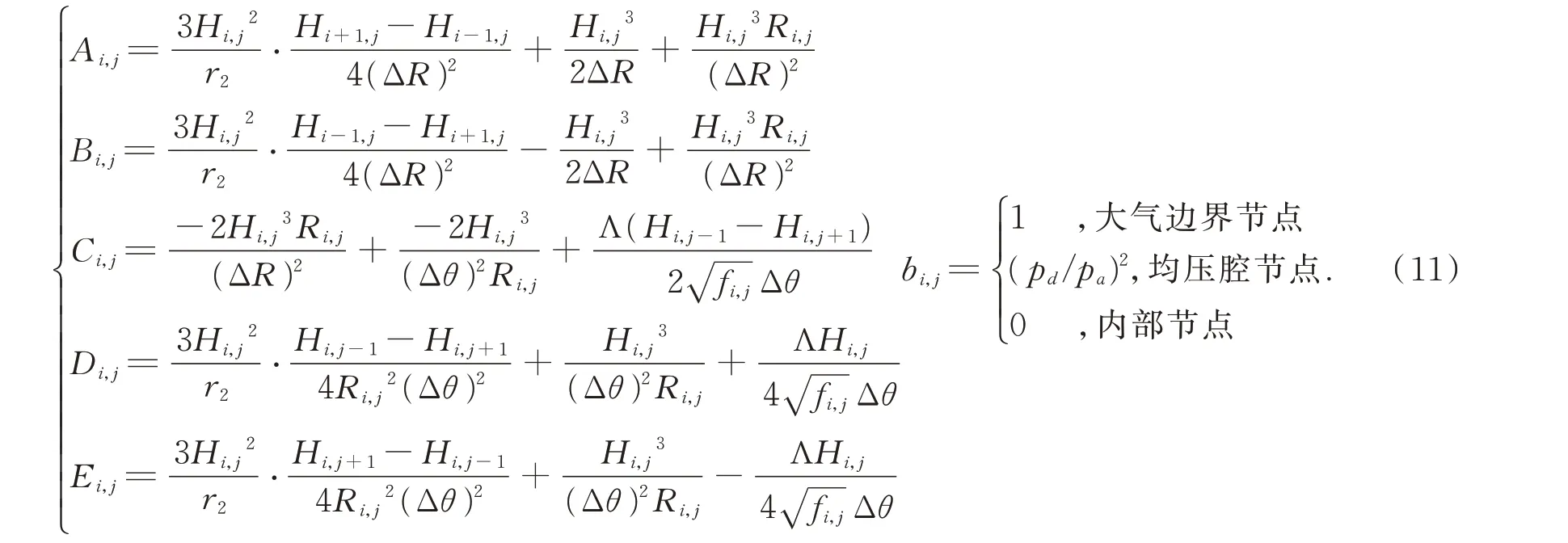
设定均压腔初始压力，结合流量平衡方程（8）便可求解离散后的雷诺方程（10），从而获得气膜厚度和压力分布，具体流程如图3 所示。将得到的压力在整个气膜面上进行积分，进而算出气膜面的承载力：

图3 气浮转台数值计算流程图Fig.3 Flow chart of numerical calculation of air-floating turntable

3 算例结果及分析

如图4 所示，将本文的计算结果和文献［22］的结果进行对比，其计算参数见表1。由图可知，两者的压力分布基本相似，从而验证文中计算程序的正确性。

表1 文献［20］计算参数Tab.1 Calculation parameters of reference［20］

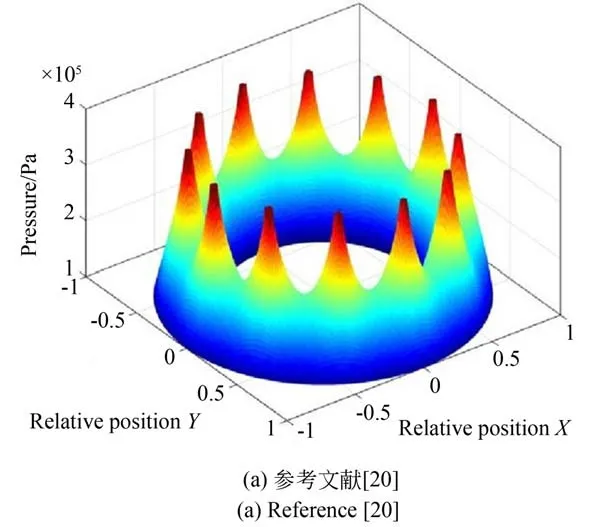
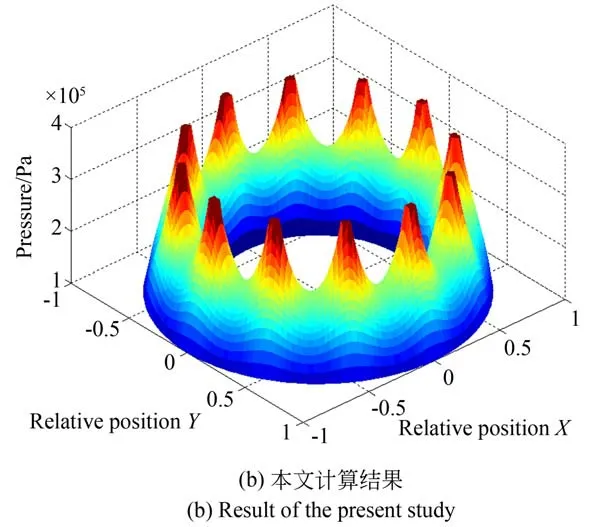
图4 气膜压力分布Fig.4 Air film pressure distribution

表2 为本文的计算参数，使用其分析角摆和转速对气浮转台气膜厚度、压力分布等静态特性的影响。

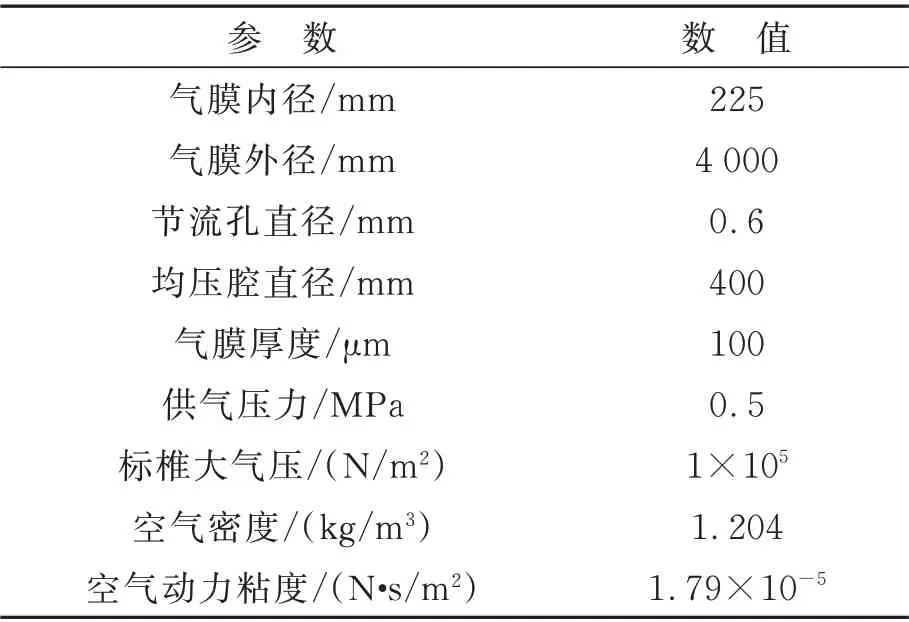
表2 本文计算参数Tab.2 Calculation parameters of the present study

3.1 单一角摆的影响

图5（a）为不同角摆ϕ下的气膜厚度，由图可知，随着角摆的增大，气膜厚度不再均匀分布。在x轴正方向（0～2 m），气膜厚度逐渐增大；在x轴负方向（-2～0 m），气膜厚度逐渐减小。这是由于气浮转台存在角摆ϕ时，气膜厚度沿y轴发生了改变。将角摆继续增大，图5（b）为不同角摆ϕ下的气膜厚度最值。由图可知，气膜厚度最大值随着角摆的增大逐渐增大，气膜厚度最小值随着角摆的增大逐渐减小。当角摆为0 rad 时，气膜厚度最大值和最小值相同都为1，当角摆达到5×10－5rad 时气膜厚度最大值为2 而最小值基本为0，这就意味着气浮转台将与支撑体表面接触，从而导致转台失效。这就说明转台角摆越大其失效的可能性越大，5×10－5rad 是本转台的最大极限角摆。

图5 气膜厚度Fig.5 Air film thickness

图6 为不同角摆ϕ下气膜面的压力分布图，由图可知，随着角摆的增大，压力不再对称分布。在x轴负方向（-2～0 m），压力随角摆的增大而增大；在x轴正方向（0～2 m），压力随角摆的增大而减小，而在y轴方向上，压力保持不变。这是由于在x轴方向上气膜厚度发生改变，气膜流场随之变化，致使气膜薄的区域压力大，气膜厚的区域压力小，而在y轴方向上气膜厚度未发生改变，因而产生这种现象。

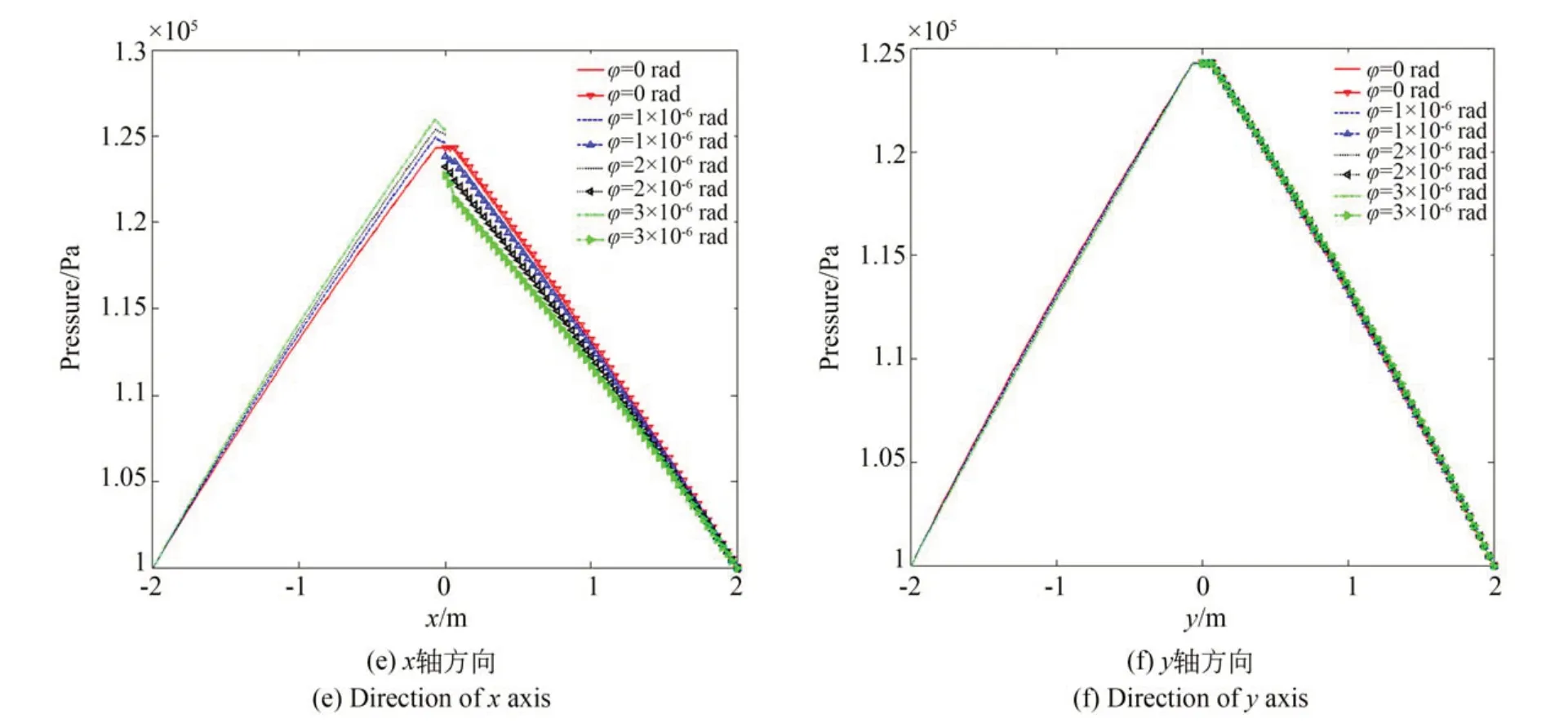
图6 气膜压力分布Fig.6 Air film pressure distribution

由于角摆的变化致使气膜厚度发生改变，从而导致整个气膜面的压力分布发生改变，而承载力为压力在气膜面上的积分，则气膜承载力势必发生改变。图7 为不同角摆ϕ下的气膜承载力，由图可知，随着气膜厚度的增大其承载力逐渐减小，这是由于气膜压力减小造成的。在同样的气膜厚度下，承载力随着角摆的增大而减小。在供气压力一定的情况下，气膜厚度是确定的，若是存在较大的角摆，则气膜承载力下降。而为了保持力的平衡，则气浮转台的位置会发生变化，从而导致超精密光学元件的表面形貌发生改变，影响加工精度。

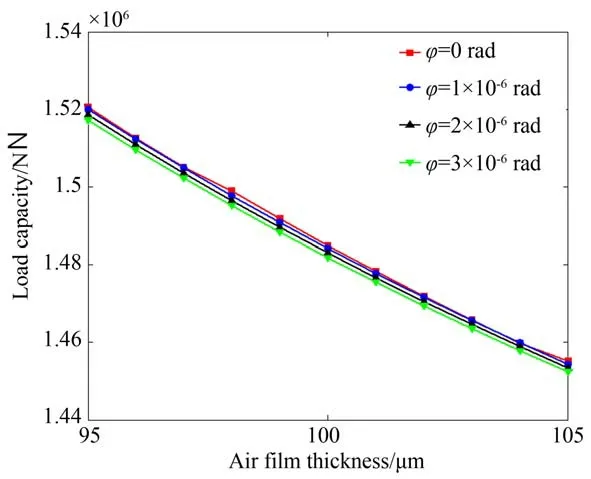
图7 承载力Fig.7 Load capacity

3.2 组合角摆的影响

气浮转台是轴对称的，因而绕x轴的角摆ψ对转台静态特性的影响和3.1 节是一致的。图8为绕x轴的角摆ψ和绕y轴的角摆ϕ同时存在时的气膜厚度，图中ψ取2×10－6rad，ϕ逐渐增大。

由图8（a）可看出，随着角摆ϕ的逐渐增大，在x 轴正方向（0～2 m）既存在气膜逐渐变厚的区域，又存在气膜逐渐变薄的区域，在其他方向也是如此，这一现象与存在单一角摆时有所不同。由图8（b）可以看出，当角摆ϕ达到4.9×10－5rad 时，气膜厚度最小值基本为0，说明4.9×10－5rad 是转台的最大允许角摆。可知，相比于单一角摆时，组合角摆下转台的活动范围更小。

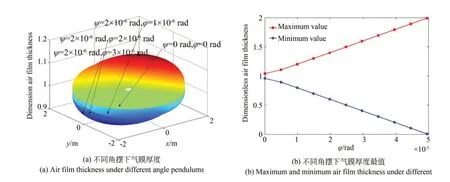
图8 气膜厚度Fig.8 Air film thickness

气膜厚度的改变必然会引起压力分布的变化从而最终导致气膜承载力的改变。图9 为不同角摆下气膜承载力，对比单一角摆情形，可看出两者规律基本一致。当角摆值从0 增大到3×10－6rad时（气膜厚度为95，100和105 μm），单一角摆下承载力下降值分别为3.423 6×10³ N，3.086 2×10³和2.841 7×10³ N，分别下降了0.23%，0.21%，0.20%。组合角摆下承载力下降值分别为4.309 9×10³，3.823 2×10³和3.437 5×10³ N，分别下降了0.28%，0.26%，0.25%。表明组合角摆下承载力下降更加显著，这是由两种情形下气膜厚度的改变不同所引起的。说明组合角摆下转台的位置改变更大，从而降低加工精度。

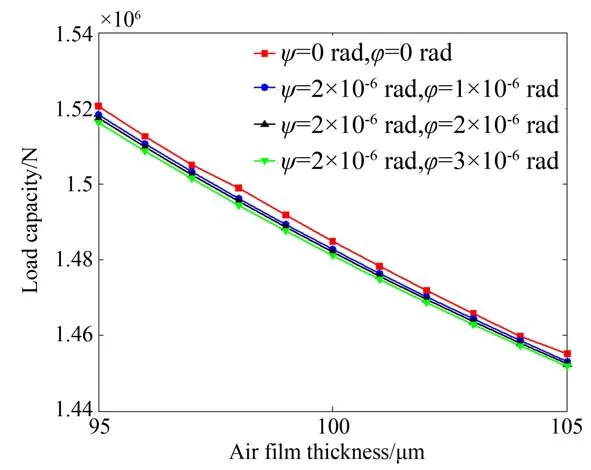
图9 承载力Fig.9 Load capacity

3.3 转速的影响

转速实则为气浮转台绕z轴的角摆，它是一个被利用的自由度。由式（2）知，转速并不直接影响气膜厚度，然而式（1）中含有转速项，说明转速不同会引起气膜压力的改变，这是由于转速改变了气膜内气体的流速，导致气膜内流场变化，从而引起压力的改变。图10 为不同转速下气膜面的压力分布。由图可知，随着转速的增大，高压区域逐渐向外均匀扩散，然而压力值却逐渐减小。由图10（e）知，当转速达到2 300 r·min-1时气膜中间均匀腔区域的压力比周围压力小，此时流量平衡方程（8）也不再满足，说明气体润滑已经失效，因而气浮转台的转速不能超过2 300 r·min-1。由于转台是轴对称结构，且压力是均匀扩散，所以图10（f）和图10（g）基本相同。

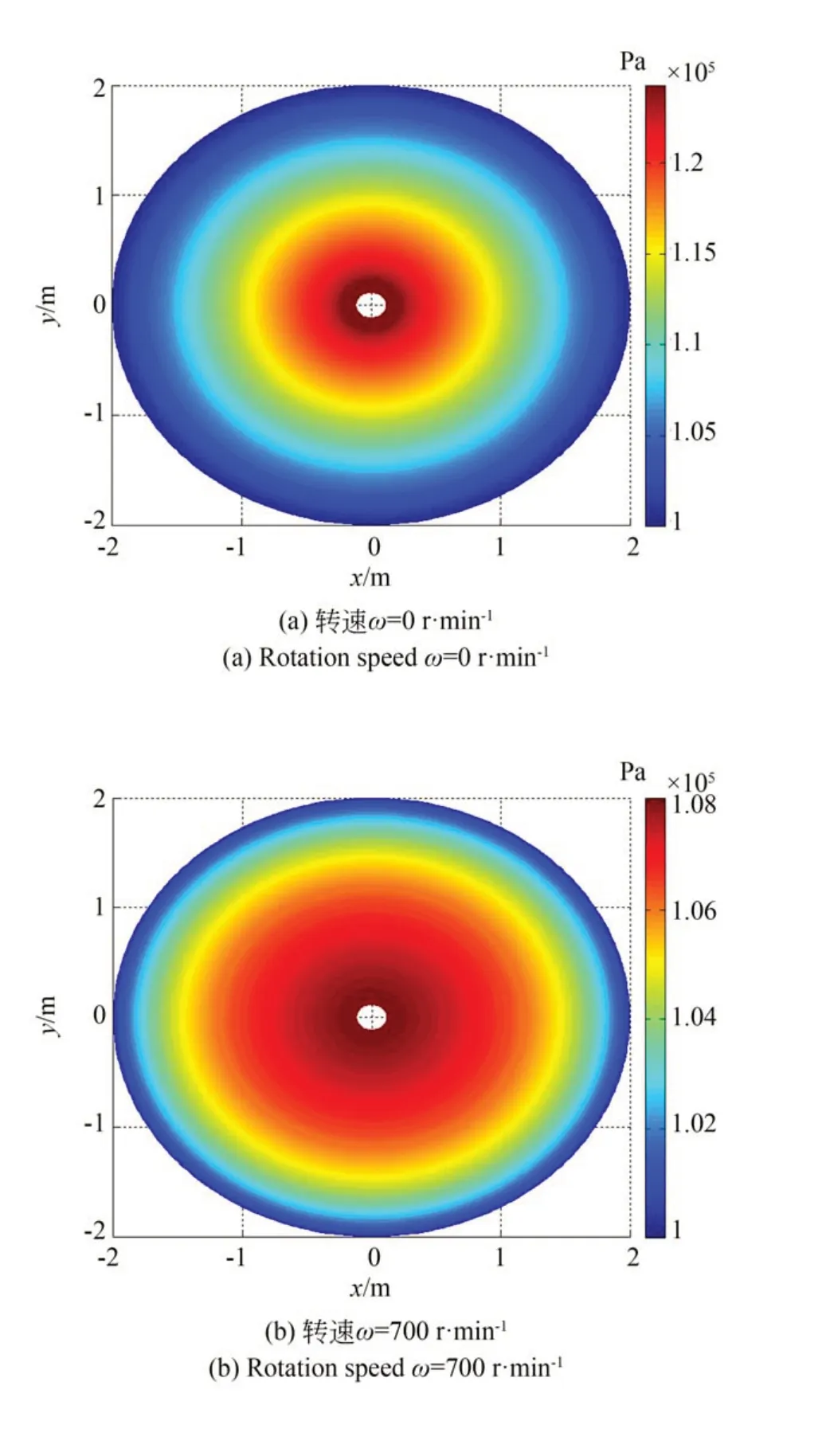
图10 气膜压力分布Fig.10 Air film pressure distribution

图11 为不同转速下的气膜承载力，由图可知，随着气膜厚度的增加，承载力在逐渐降低，这与前面的分析一致。在相同气膜厚度时，承载力随转速的增大而降低，当转速从0 增大到2 100 r·min-1时（气膜厚度为95，100 和105 μm），承载力下降值分别为2.038 0×105，1.750 2×105和1.496 1×105N，分 别 下 降 了13.40%，11.79%，10.28%，说明转速的大幅度增大会引起承载力的快速下降。这可能是由于随着转速的提高，静压效应减弱，动压效应增强，而此时减弱幅度大于增大幅度，因而承载力降低。

图11 承载力Fig.11 Load capacity

在实际工作中增大转速可以提高加工效率，然而转速的增大会导致承载力的下降。参见表2，在供气压力为0.5 MPa 时气膜厚度为100 μm。由图11 知此时若将转速从0 增大到2 100 r·min-1，则承载力由1.485×106N 减小到1.310×106N。工作时气浮转台在空间中处于悬浮状态。转台的质量一定，为了达到1.485×106N 的承载力，由图12 知气膜厚度会减小到47.5 μm，而此时转台的最大极限角摆为2.37×10－5rad，与之前的5×10－5rad 相比，其值大大减小。因而，将转速增大2 100 r·min-1需将角摆减小2.63×10－5rad，应考虑减小或消除致使产生角摆的因素，比如降低偏载质量等。否则，会引起转台和支撑体表面接触。此外，转台转速也不能无限增大，当转速超过2 300 r·min-1后，由于气体润滑失效，气浮转台也会无法工作。

图12 承载力和气膜厚度最值Fig.12 Load capacity and maximum and minimum air film thickness

4 实验测量

实验测量气浮转台角摆，采用激光位移传感器，将传感器吸附在大字形支架上，传感器探头对应抛光圆盘平面，圆盘静止不动，安装如图13所示。气浮转台在底部不供气时，此时的坐标系设定为参考平面，即0 初始位置。测量时，供气压力为0.5 MPa，同时启用三个传感器测量，通过移动修正盘的位置可以改变抛光圆盘的倾角，一次测量得到三个位置高度信息。并对三个传感器建立水平位置坐标系，结合高度信息建立三维空间坐标系。因为抛光圆盘为大理石材质，可以将其视为刚体，所以通过三个点可以建立一个圆形测量平面，其平面的倾角即为转台的角摆。通过计算可以得到圆盘最高位置以及最低位置点即气膜厚度最大值和最小值，计算结果如表3所示。

图13 气膜厚度实验测量平台Fig.13 Experimental measurement platform of air film thickness

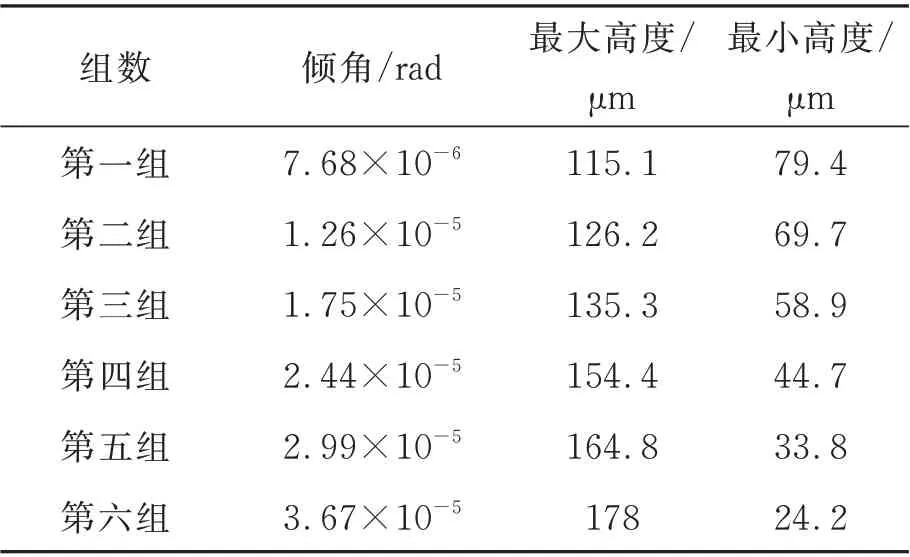
表3 实验测量圆盘位置最值Tab.3 Highest and lowest value of the experimental measurement disc position

将实验测量数据进行无量纲化处理，图14 为实验和理论对比图，由图可知两者规律基本一致，最大误差为14.4%。考虑到转台和测量平台的制造及安装误差，可以认为理论数值计算和实际实验是吻合的。

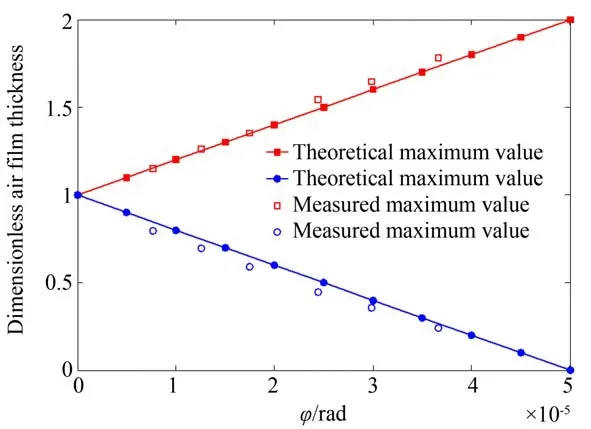
图14 气膜厚度最值的实验和理论对比Fig.14 Experimental and theoretical comparison of the maximum and minimum air film thickness

5 结 论

本文根据超精密全口径抛光机气浮转台在实际工作时会存在倾斜角摆和一定转速的特点，将考虑角摆后的气膜厚度方程带入雷诺方程，得到含角摆和转速的雷诺方程。然后采用有限差分法将雷诺方程离散化处理，并结合流量平衡方程进行求解，通过和现有文献结果的对比验证程序的正确性。最后得到了单一角摆、组合角摆和不同转速下气膜厚度、压力分布以及承载力这些静态特性并通过实验加以验证。结果表明：随着角摆的增大，气膜厚度会发生改变，5×10－5rad是单一角摆下转台的最大极限角摆。气膜厚度的改变影响压力分布，最终导致承载力的下降；组合角摆下转台的最大极限角摆为4.9×10－5rad，组合角摆对转台静态特性的影响更为显著，但其影响规律和单一角摆时基本一致；随着转速的增大，气膜压力分布发生改变，承载力逐渐下降，当转速超过2 300 r·min-1后，气体润滑失效，这就是转台的失效转速。角摆和转速的改变致使气膜承载力发生变化，为了保持力的平衡，转台的位置也会随之改变，从而影响超精密光学元件的加工精度。在实际工作中若将转速增大2 100 r·min-1则应将最大极限角摆减小2.63×10－5rad，同时也要设法消除角摆以提高气膜厚度的均匀性，从而降低承载力的波动以提高加工精度。该研究为后续双向流固耦合研究气浮转台的动态回转误差提供了理论基础。