TDLAS 一氧化碳浓度检测系统误差分配

潘 云，李 颐，颜昌翔，3*

（1. 中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2. 中国科学院大学，北京 100049；3. 中国科学院 大学材料与光电研究中心，北京 100049）

1 引 言

热电厂燃料不完全燃烧产生的一氧化碳（CO）是一种有毒气体，也是间接导致温室效应的气体。研究表明，热电厂在完全燃烧的条件下，CO 含量为50×10-6～90×10-6，氧量不足会导致CO 含量指数增长，可达1%量级。监测燃烧产生的CO 浓度有利于减少有害气体的排放，同时可以从中反映空燃比，调整燃料的用量以达到节能的目的［1-3］。

为了实现对CO 气体浓度的实时监测，利用可调谐二极管激光吸收光谱（Tunable Diode Laser Absorption Spectroscopy，TDLAS）技术进行测量。近年来，TDLAS 技术由于其高选择性、高灵敏度、高响应速度等优点，广泛应用于气体浓度、温度及速度等参数的测量中［4-11］。由于TDLAS 浓度测量系统存在多种系统误差和随机误差，对于短光程气体浓度的测量精度在1%～5%［12-14］。为了降低测量误差，李峥辉、李金义等分别对测量过程中的温度、压强变化进行修正［15-16］，Upadhyay 等对光强等激光器自身参数进行实时在线标定［17］，王振等对CO 气体分子碰撞展宽等谱线参数进行了标定［18］。上述研究在气体浓度测量方面取得了一些成果，但是还存在较大的测量误差。而且上述对于TDLAS 测量的误差研究大多是针对单项误差的分析和修正，没有对测量系统各项误差及其影响进行全面的分析，也没有给出对系统总体的误差分配。

为了降低多种误差因素的影响及仪器的设计难度和成本，本文提出了一种误差分配方法。根据二次谐波信号反演气体浓度的原理，建立了TDLAS 系统的误差模型，利用随机化方法分析了各个误差项对浓度测量的影响，并通过数值拟合的方法比较了浓度误差对各项误差变化的灵敏度；最后根据求得的灵敏度关系，结合热电厂CO 浓度的测量需求和现有器件的工艺水平，对系统各项误差进行了合理分配。本文的研究结果对TDLAS 浓度测量系统的各项误差分配给出了指导，对于仪器研发具有重要的参考意义。

2 测量原理

2.1 TDLAS 系统组成

在TDLAS 技术中，根据二极管激光器的波长调谐特性，通过改变二极管激光器的注入电流，扫描被测气体的单个特征吸收谱线，从而对气体浓度进行测量。TDLAS 技术包括直接吸收光谱（Direct Absorption Spectroscopy，DAS）技术和波长调制光谱（Wavelength Modulation Spectroscopy，WMS）技术［19］，其中WMS 技术因具有更高的检测精度而受到更广泛的应用。在WMS 技术中，激光器波长受低频锯齿波扫描信号和高频正弦波调制信号的共同作用，光束通过气体吸收后，利用锁相放大器对透射光强信号进行谐波检测，获得包含气体吸收的信息。典型的TDLAS 浓度检测系统如图1 所示，主要包括光源模块、气体吸收模块和信号检测模块。

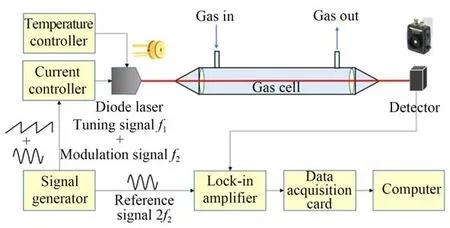
图1 可调谐二极管激光吸收光谱系统组成Fig.1 Block diagram of TDLAS system

2.2 浓度测量原理

在WMS 技术中，注入高频正弦调制信号（角频率为ω，ω= 2πf）后的激光输出频率-时间响应表示为［20］：

其中：νˉ为激光器扫描过的中心频率，νm为激光器波长调制幅度，由激光器调制特性可知其值与正弦波调制电流的幅度im成正比，其比例系数为ki。

考虑激光器的频率调制-光强调制（FM-IM）相位差，输出的瞬时光强为：

式中：I0为扫描过的激光平均光强；Im为激光器线性光强调制幅度，其值不随激光扫描光强的变化而变化，而是与波长调制幅度νm成正比；ψ为线性光强调制与频率调制之间的相位差。

当激光通过待测气体时，其透射光强和初始光强满足Lambert-Beer 定律，透射光强表示为：

式中：P为混合气体的总压强，S（T）为温度T下的气体吸收谱线的线强，ϕ(ν)为气体吸收线型函数，C为待测气体的体积分数，L为有效光程，α（ν）为光谱吸光度。α( )ν可 展 开 为Fourier 余 弦级数形式，即：

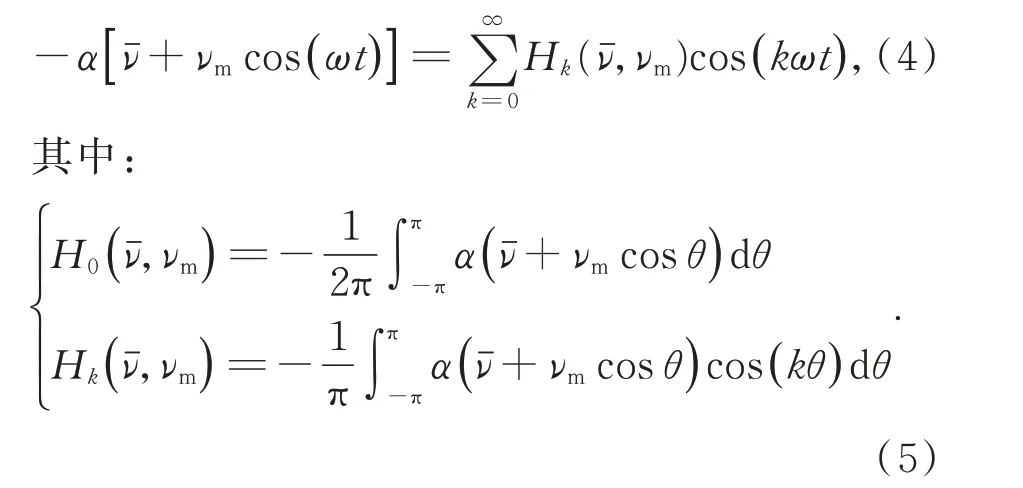
联立式（2）～式（4），可得透射光强的表达式如下：

其中：S（T0）为常温下的线强，T0=296 K，h为普朗克常数，c0为真空中光速，kB为玻尔兹曼常数，E''为分子跃迁的低态能量，ν0为分子吸收谱线的中心频率，Q（T）为配分函数。Q（T）可从HITRAN 数 据 库［21］得 到，它 与 温 度 的 拟 合 关 系 式如下：

气体吸收线型函数采用Lorentzian 线型来描述［22］：

其中：γL（T0）为压力展宽系数，n为温度指数，对于CO 气体n取0.69。

定义两个无量纲参数：

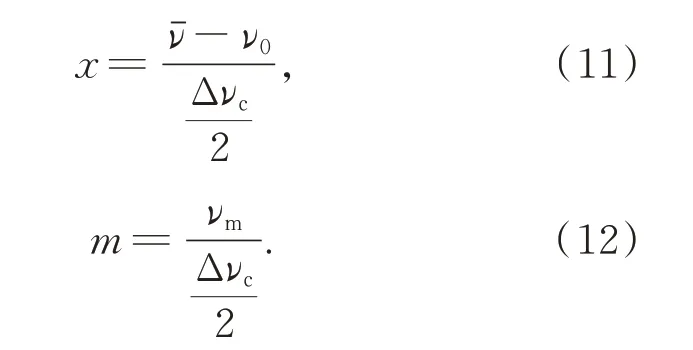
其中：x为归一化中心频率失谐量，m为调制深度。则式（5）可写为：

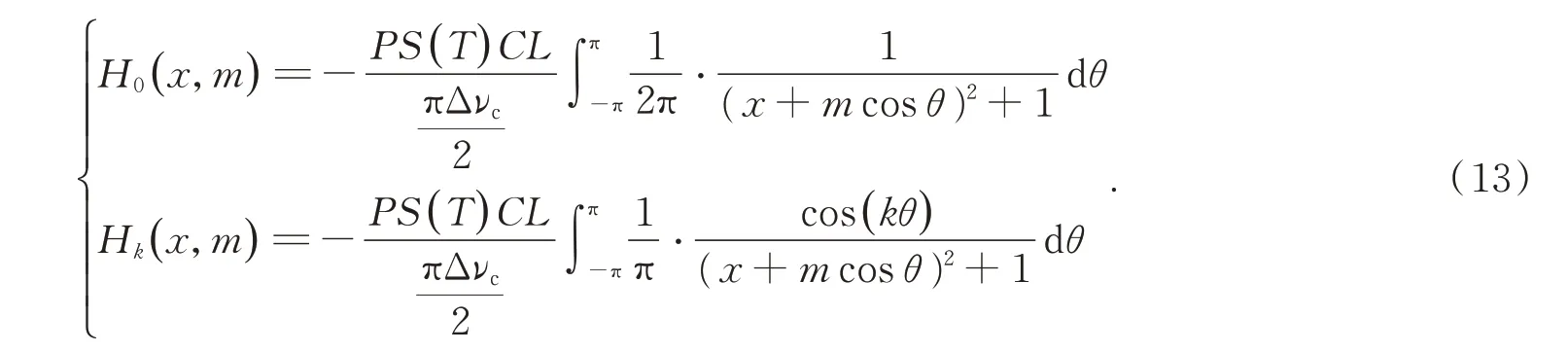
其简化表达式由Axner 等给出［23］。

用于提取二次谐波的锁相放大器的参考信号如下：

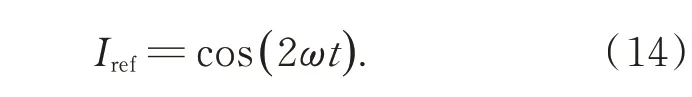
经过锁相放大器及低通滤波器后，最终采集到的扣除基线的二次谐波信号表达式X2f－0如式（15），波形如图2 所示。

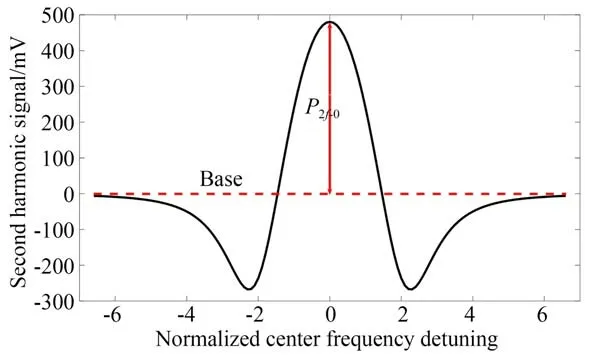
图2 二次谐波信号波形Fig.2 Waveforms of second harmonic signal

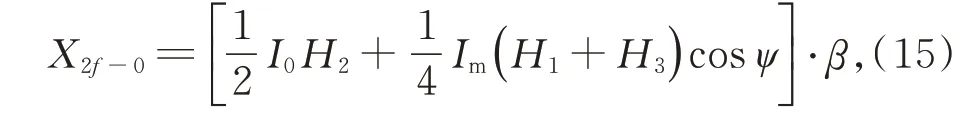
其中β为探测器光电转换系数与锁相放大器增益的乘积。

当x=0 时，二次谐波有最大值P2f-0，此时H1=H3=0，H2表达式如下：

3 系统误差分析与分配

3.1 误差模型建立

从式（16）中可以看出，浓度的误差与P2f－0，Δνc，I0，P，S（T），L，m等变量有关，而由2.2 节可知，Δνc是温度T和压强P的函数，S（T）是温度T的函数，m是波长调制幅度νm和温度T及压强P的函数，而波长调制幅度νm与电流调制幅度im成正比，因此最终影响浓度的误差项可归结为P2f－0，I0，im，P，T，L6 项，其误差分别记为ΔP2f－0，ΔI0，Δim，ΔP，ΔT，ΔL，由此带来的浓度的绝对误差记为ΔC。

Δνc，S（T）和m引入误差后的表达式分别为：

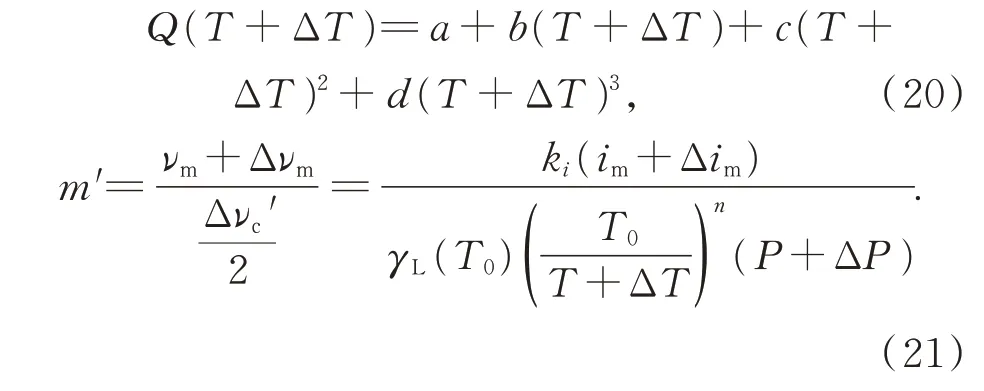
式（17）是P2f－0，I0，im，P，T，L6 个变 量的函数，简化表达式得到：

包含误差的浓度表达式为：

因此浓度的绝对误差为：

这6 项误差中，ΔP2f－0，ΔP，ΔT与测量器件精度有关；I0项由于受到激光器功率波动、电厂管道灰尘等的影响，一般采用一次谐波信号对二次谐波信号进行归一化的方法消除其影响［24］，因此ΔI0与归一化标定误差有关；Δim是调制电流的稳定性；光程L项受管道形变和抖动的影响，因此ΔL是光程的稳定性。

3.2 浓度误差对各项误差的灵敏度分析

浓度误差模型不仅包含线性项，还包含高次项和指数项，直接利用微分法难以推导浓度误差与其他各项误差的关系，因此本文采取随机化方法对各项误差进行数值拟合。该方法利用随机抽样统计来估算结果，对于解析法难于求解的问题，基于样本即可进行统计处理，得到有关概率分布，作为问题的解。

固定其他误差项为0，对要分析的误差项，设置其极限误差取值从0 开始到某个值，对该区间内的每个取值，生成一系列正态分布的随机数，其均值为0，方差为该极限误差的1/3，根据式（24）在Matlab 中计算得到一系列浓度误差，统计其分布并根据3σ准则计算相应的浓度极限误差，由此得到各误差项取不同极限误差时的浓度极限误差。在计算中，设置气体浓度为2.5%，激光强度为13.26 mW，调制电流幅度为2.5 mA，气体总压强为1×105Pa，温度为296 K，光程为100 cm，β为3.785×104V/W，二次谐波峰值为508.7 mV。分析各项误差取不同值时的浓度误差并做散点图，结果如图3 所示。

图3 各项误差对浓度的影响Fig.3 Effect of each error on concentration error

对图3 中浓度误差与各项误差进行数值拟合，得到：

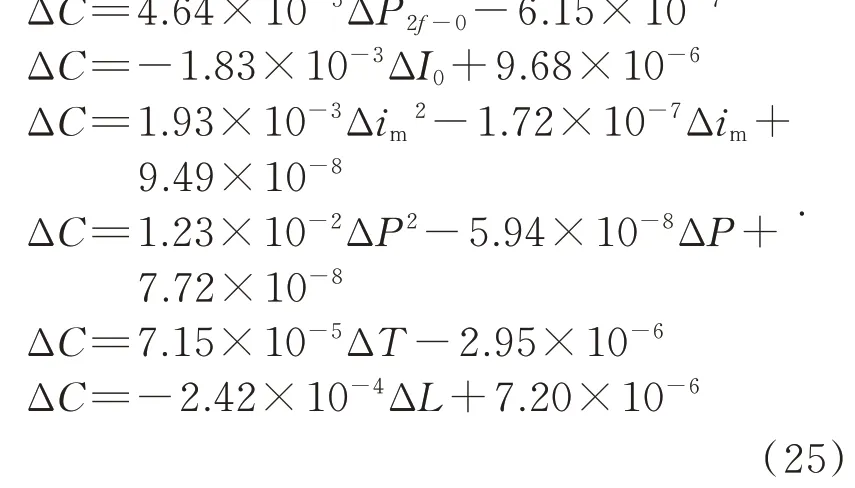
由图3 和式（25）可以看出，各项误差对浓度的影响形式和程度均不一样。其中，Δim和ΔP两项与ΔC的拟合式为二次函数，ΔC在10-5量级，而其他4 项的拟合式为线性函数，ΔC可达10-3量级。由于Δim和ΔP两个二次项的影响远小于其他4 项，在进行灵敏度分析时不予考虑，而其他4项误差的影响用灵敏度来进行比较。对于4 个线性误差项，灵敏度定义为：

其中ΔX代表各项误差，可见灵敏度即为一次曲线斜率的绝对值。灵敏度越大，误差项对浓度误差的影响越大。最终各项误差的灵敏度如表1所示。

由表1 可知，浓度对各项误差变化的灵敏度由大到小依次为：ΔI0＞ΔL＞ΔT＞ΔP2f－0＞ΔP＞Δim。各项误差的分配将参考此灵敏度关系进行，其中ΔI0和ΔL的灵敏度最大，因此主要控制这两项误差，在保证总体误差达标的情况下其他项可以适当放宽，以降低仪器的设计难度，节约成本。

表1 浓度误差对各项误差变化的灵敏度Tab.1 Sensitivities of concentration error to each error

3.3 各项误差分配

基于各项误差的灵敏度、当前工艺水平和经济成本等，对各项误差进行分配。对体积分数为2.5% 的气体，要求测量的绝对误差不超过0.025%。目前常用的示波器，如Tektronix、Keysight、NI、LitePoint 等，其 垂 直 精 度 在0.25%～2.5%［25］，对500 mV 左右的信号，误差在2 mV 左右可满足要求。对I0的归一化标定的相对误差可小于1%，激光器驱动器常用Wavelength、ILX、Newport、Thorlabs 等品牌，其电流精度一般在0.005～4 mA 之间，根据灵敏度关系，对电流稳定度的要求可以放低，此处取0.02 mA 即可满足要求。压力传感器精度在0.01%～10%之间可分为4 个等级，常用的压力传感器如Honeywell、Keller 等，其精度在0.05%～0.5%，由于压强误差对浓度误差的影响较小，采用常见的精度为0.5%FS、量程为1 MPa 的压力传感器，最大误差为0.05×105Pa 即可满足要求。常用的电偶式温度传感器精度在0.1～5 K 之间，取1 K。光程误差主要由管道的振动和温度变化引起的形变导致，热电厂管道由于振动产生的位移在0.3 cm左右［26］，而管道材料通常为钢材，其热膨胀系数在10×10-6～20×10-6/K，管 壁 厚 度 在2 cm 左右，温度变化导致的管道形变相比于振动产生的位移小两个数量级，因此光程稳定性取0.4 cm。最终各项误差的概率分布及分配的极限误差值如表2 所示。

表2 各项误差分配Tab.2 Distribution for each error

4 仿 真

4.1 仿真方法

为了综合分析各项误差影响下的浓度误差，在Matlab 编程环境下用蒙特卡洛法［27］对上述误差分配方案进行仿真。蒙特卡洛法又称统计试验法，采用随机数对解析法难以求解的问题进行统计模拟。针对TDLAS 气体检测系统的误差分析，蒙特卡洛法仿真的关键在于对各项误差构造一系列随机数，计算由此产生的一系列浓度的测量误差，统计其概率分布，将概率刚好大于99.73%时的浓度误差作为测量的极限误差，仿真流程如图4 所示。

图4 蒙特卡洛法仿真流程Fig.4 Flowchart of Monte Carlo simulations

4.2 仿真结果

将表2 中各项误差因素以正态分布的形式代入式（24）中，利用蒙特卡洛法对浓度误差进行仿真，得到浓度误差的统计直方图，如图5 所示。

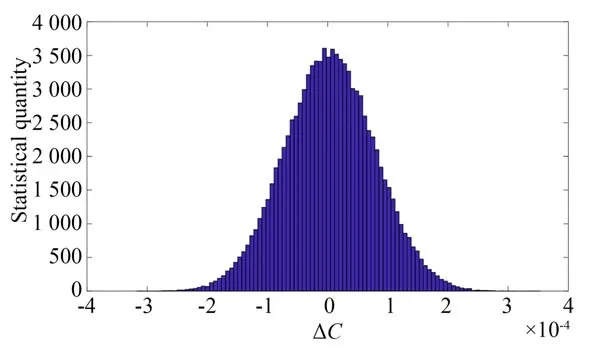
图5 浓度误差的统计直方图Fig.5 Histogram of concentration error

由图5 中可知，浓度误差统计数量服从正态分布，在100 000 次仿真结果中，浓度极限误差小于0.025%的次数为99 742 次，概率为99.74%。根据3σ原则，设置置信概率为99.73%（3σ），在此概率下ΔC的取值几乎全部集中在（-3σ，3σ）区间，仿真得到的置信区间为（-0.023%，0.023%）。此由可知，在各项误差分布以及误差值符合表2 的情况下，浓度的极限误差小于0.025%，相对误差小于1%，满足指标要求。

5 实 验

5.1 实验装置

图6 所示为利用TDLAS 技术测量CO 浓度的实验装置。系统由一个三通道的直流电源供电（GWInstek，GP-3323）。采用高精度激光驱动器（Wavelength，LDTC0520）来驱动激光器，它包括电流驱动和温度控制两个部分。激光器采用中心波长在1 566 nm 附近的DFB 激光器（Eblana，EP-1566-DM-TP39），光强约为10 mW。激光经过1 m 长的不锈钢气体池后，被峰值响应在1 550 nm 附 近 的Ge 光 电 探 测 器（Thorlabs，PDA30B2）接收。探测器的输出端与锁相放大电路相接，包括信号发生和锁相放大两个功能。最后采用示波器（Angilent，MSO6104A）与锁相放大电路相连，用于记录二次谐波信号。实验中所用的一氧化碳气体浓度为2.5%，实验温度为296 K，压强为1×105Pa，各参数均与仿真一致。

图6 TDLAS 浓度测量实验装置Fig.6 Experimental setup of TDLAS concentration measurement

5.2 实验结果

实验中对CO 浓度进行了10 组测量。最终得到的二次谐波峰值和反演的浓度值如表3所示。

从表3 中可以看出，浓度的绝对误差均在（-0.01%，0.01%）内，相对误差在（-0.4%，0.4%）之间，10 组测量结果的均方根误差（Root Mean Square Error，RMSE）为8.069×10-5。测量结果显示，浓度极限误差小于0.025%，相对误差小于1%，与仿真结果一致，满足测量要求，而且测量结果的重复性也比较高。

表3 实验测量二次谐波峰值和浓度反演数据Tab.3 Second harmonic values measured in experiments and concentration inversion data

6 结 论

利用TDLAS 技术对热电厂管道中CO 浓度进行检测时，容易受到光强、温度及压强等的影响，测量浓度存在误差。本文针对系统整体的误差分配问题，首先建立了浓度反演的误差模型，准确引入了各误差项；其次，利用随机化方法分析了各项误差对浓度误差的影响，比较了浓度误差对各项误差变化的灵敏度；最后，根据此灵敏度关系和现有的器件工艺水平对各项误差进行了分配。基于蒙特卡洛法的仿真结果表明，对2.5%体积分数CO 测量的极限误差为0.023%；实验室测量结果表明，浓度的绝对误差小于0.01%，与仿真结果一致，证明了误差分配方案的有效性，在满足热电厂测量要求的同时降低了仪器成本和设计难度。本文的研究结果可为TDLAS 浓度检测系统的设计与误差分析提供关键的理论指导，对仪器的研发与应用具有重要的参考价值。

本文的研究在仪器误差分配和浓度测量方面取得了一些效果，但是在实验方面还存在一些不足之处。本文只对2.5%浓度的CO 气体和固定温度压强条件进行了实验验证，适合热电厂在不完全燃烧条件下的应用。为了进一步扩大仪器的应用范围，后续将对低浓度的气体和温度压强等环境条件变化的情况进行实验研究。