Zeilberger算法与二项分布

张雅恬， 刘世凤， 张亚南

(天津理工大学 理学院，天津300384)

1 引 言

20世纪90年代，组合学家Wilf和Zeilberger给出了WZ理论[1]，该理论是证明组合恒等式的一种机械化方法.其中的Zeilberger算法是寻找和式的线性递推关系的一种方法，利用和式的递推关系可以对和式进行化简和证明.

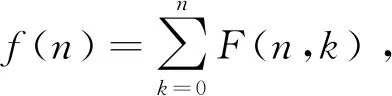
首先，需要找到一个关于n,k的有理函数R(n,k)和关于n的多项式系数c0(n),c1(n),…,cp(n)满足

c0(n)F(n,k)+c1(n)F(n+1,k)+…+cp(n)F(n+p,k)=g(n,k+1)-g(n,k),

(1)

其中p为自然数，g(n,k)=R(n,k)F(n,k).

可利用maple软件包hsum15.mpl(可以从http:∥www.mathematik.uni-kassel.de/～koepf/hsum15.mpl下载)求得R(n,k),c0(n),c1(n),…,cp(n).

然后，上式两边关于k从0到n+p求和，即

整理得

c0(n)[f(n)+F(n,n+1)+…+F(n,n+p)]+…+cp(n)f(n+p)=g(n,n+p+1)-g(n,0).

于是得到一个仅跟n有关的递推关系

c0(n)f(n)+c1(n)f(n+1)+…+cp(n)f(n+p)=-g(n,0),

当p=1,g(n,0)=0时，可递归算得f(n).

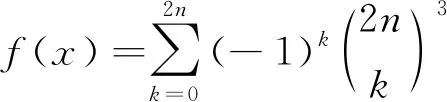
2 二项分布的高阶矩

在概率论中高阶矩[4]是一个常见且非常重要的概念，它主要被用来衡量误差的大小.其中一阶矩被称为数学期望，二阶中心矩被称为方差.

设X服从二项分布B(n,p), 分布律为

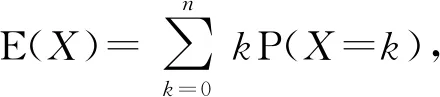
定理1设X服从二项分布B(n,p), 则E(X)=np.

证令

利用hsum15.mpl软件包中的sumrecursion命令求解，得到

-nF(n+1,k)+(n+1)F(n,k)=g(n,k+1)-g(n,k),

其中g(n,k)=R(n,k)F(n,k), 上述等式两边对k从0到n+1求和可得

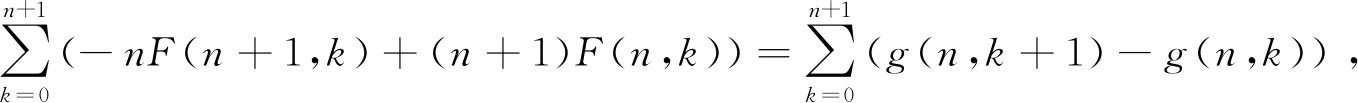
定理2设X服从二项分布B(n,p), 则方差D(X)=np(1-p).

证令

由sumrecursion命令求得

-n(pn-p+1)F(n+1,k)+(pn+1)(n+1)F(n,k)=g(n,k+1)-g(n,k),

其中g(n,k)=R(n,k)F(n,k). 上式两边对k求和，得

-n(pn-p+1)f(n+1)+(pn+1)(n+1)f(n)=0，

则

由递推关系可知：f(n)=n(pn-p+1)f(1). 由于f(1)=p, 则f(n)=n(n-1)p2+np.

即E(X2)=n(n-1)p2+np. 由定理1知E2(X)=n2p2, 所以

D(X)=E(X2)-(E(X))2=n(n-1)p2+np-n2p2=-np2+np=np(1-p).

由同样的方法可得超几何分布的期望和方差，并且还可求得二项分布的m阶矩，比利用m阶矩的递推公式[5-6]计算更直接.

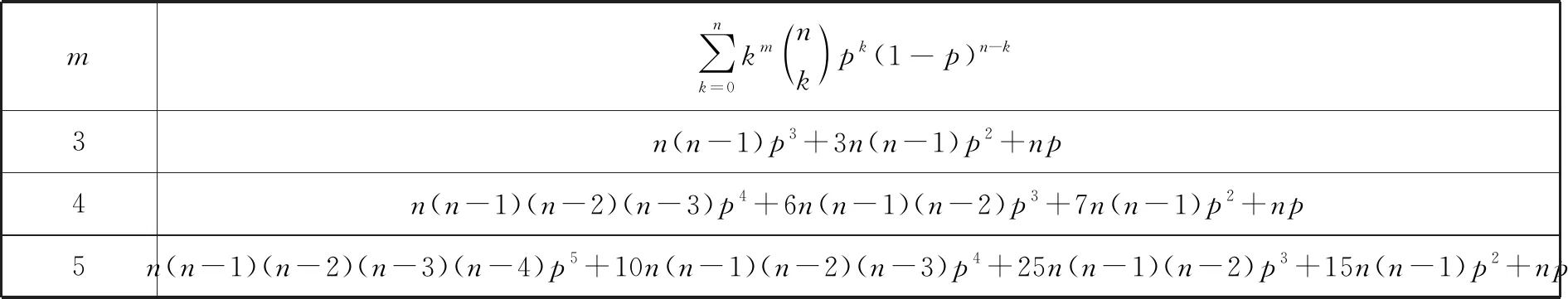
表1

3 探究形如的和式

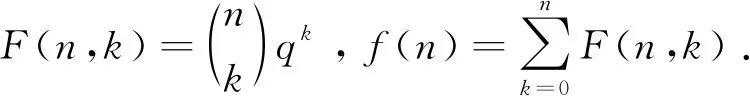
计算得到f(n+1)=(1+q)f(n),f(1)=1+q. 由此递推得出f(n)=(1+q)n.

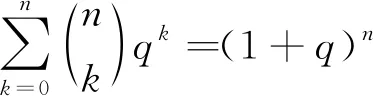
利用sumrecursion命令，部分结果如下表：

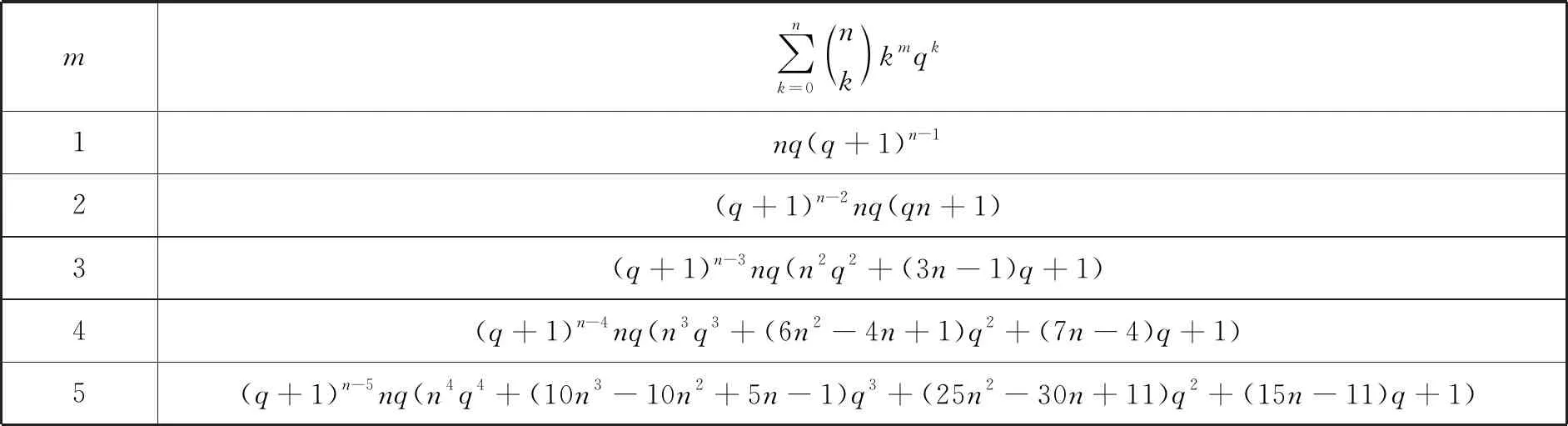
表2

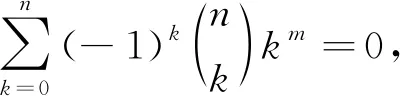
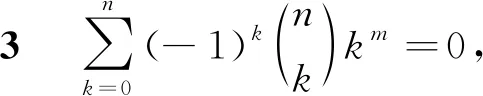
证由于

是k的m次多项式，则

其中c0,c1,…,cm与k无关.

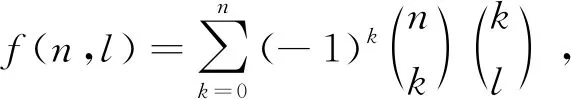
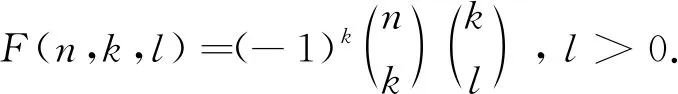
-(-n-1+l)(lσ1-nσ1+n)F(n+1,k,l)+(n+1)(l-n)F(n,k,l)=g(n,k+1,l)-g(n,k,l),

其中σ1是自由量，令σ1=0, 得

(n+1-l)nF(n+1,k,l)+(n+1)(l-n)F(n,k,l)=g(n,k+1,l)-g(n,k,l).

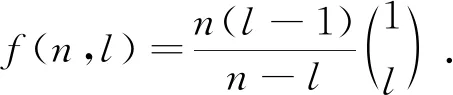
l=1时，f(n,l)=0.

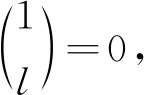
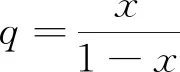
令

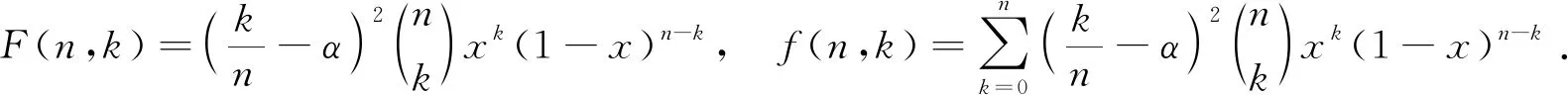
由sumrecursion命令求得

-(n+1)(α2n-2αnx+nx2-x2+x)F(n+1,k)+n(α2n-2αnx+nx2+α2-2αx+x)F(n,k)
=g(n,k+1)-g(n,k)

+4α2kn2x-2αkn2x2-2α3kn+2α3n2+α2k2n+4α2knx-3α2n2x-α2nx2-2αk2nx

+2αn2x2+k2nx2+2α3n+α2k2-2α2kn-α2kx-2α2nx-2αk2x+2αknx+2αkx2

-2knx2-α2k+α2x+2αkx-2αx2+k2x-kx2+nx2-kx+x2)(-1+x)kn)，

其中g(n,k)=R(n,k)F(n,k). 上式两边对k求和，得

-(n+1)(α2n-2αnx+nx2-x2+x)f(n+1)+n(α2n-2αnx+nx2+α2-2αx+x)f(n)=0,

则

由递推关系可知

其中f(1)=α2+x-2αx.则

注 [7]中将该求和项中的(k-nα)2分解成三项之和

(k-nα)2=n2α2-(2nα-1)k+k(k-1)，

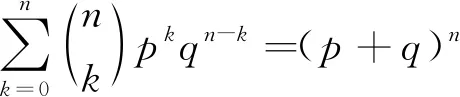
5 结 论

利用Zeilberger算法寻找递推关系式，从而求解和式.这一方法可以用来计算概率分布中的k阶矩，以及解决高等数学中一些级数求和问题.本文主要给出二项分布的高阶矩求解，这一方法还可以用来求解超几何分布和其他离散型分布的高阶矩.对于复杂的和式求解问题也可以参考该算法.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.