一种集成可靠性估计与状态监测数据的带式输送机托辊维护决策

张宝龙

(平顶山天安煤业股份有限公司，河南 平顶山 467000)

0 引言

带式输送机系统的可靠性对矿井煤炭运输部门安全管理有重要作用[1]。系统可靠性可以看作是整体结构中各部件(输送带、滚筒、传动装置和托辊等)的综合可靠性，预防性维护是保证带式输送机系统可靠性的重要环节[2]。输送带、滚筒和传动装置的维护决策已被广泛研究，例如基于轴承的故障检测对于滚筒的维护决策，以及通过监测温度和振动两个主要参数对滑轮的维护决策。对于驱动装置，学者们介绍了基于模型的变速箱监测与诊断方法[3]。然而，目前对带式输送机系统中空间分布的托辊进行预防性维护决策的研究较少，托辊的失效形式主要有轴承失效和辊壳磨损两种，其中轴承失效造成的后果更严重[4]。

轴承可靠性理论是托辊可靠性评估的基础，学者们研究了轴承的各种失效模型如泊松分布、泊松指数分布、威布尔分布和对数正态分布等[5]。然而，在没有历史维修数据或先验知识的情况下，这些理论可靠性模型中的参数很难确定。此外，模型仅提供托辊总体的可靠性估计，而对于个别故障托辊的判别无能为力[6]。温度是滚动轴承故障的直接有效指标，目前温度信号的诊断都是基于阈值的方法，诊断是通过评估监测参数的值是否超过假定的阈值来实现[7]。然而，滚动轴承的温度随轴承、负载、转速和环境而变化。因此，设定一个通用的托辊诊断阈值是非常困难的，这种方法需要深入了解状态数据与物理劣化之间的关系，而物理劣化通常比较缺乏。

本文将可靠性理论估计与状态监测数据相结合，提出了一种带式输送机系统托辊的综合维护决策架构，该决策架构中的诊断阈值可以根据托辊实时运行条件和可靠性估计结果而变化，实现了以可靠性为中心的托辊预防性维护准确决策。

1 维护决策架构

为了实现带式输送机系统托辊的预防性维护，提出了一种带式输送机托辊的维护决策架构，如图1所示。

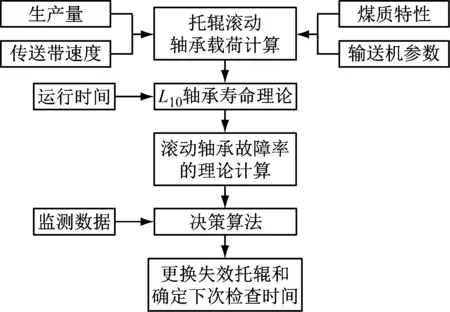
图1 维护决策框架

该维护决策框架的核心包括4部分内容，分别为托辊滚动轴承寿命计算、轴承寿命理论、滚动轴承故障率的理论计算和决策算法，它们集成了托辊的工况信息、可靠性评估和状态监测数据。带式输送机系统中的托辊均含有一个状态监测系统，用于监测托辊的承载压力、转速、温度等信息参数，通过对实时监测数据和历史数据进行计算分析，实现托辊的预防性维护决策，可以诊断哪些托辊将出现故障，以及确定下一次检查时间。

图1表明了带式输送机系统托辊的预防性维护决策流程，首先根据煤炭的生产量、煤质特性、输送机参数和传送带速度计算托辊中的滚动轴承载荷，利用滚动轴承的运行时间和L10轴承寿命理论确定托辊滚动轴承的剩余寿命。然后通过理论计算获得托辊滚动轴承的故障率，结合采集的状态监测数据，输入到开发的决策算法中分析。最后判别出现故障的托辊并更换，以及确定下次检查的时间。在维护决策流程中，滚动轴承故障率计算和决策算法是决策过程中的两个重要阶段。

2 故障率计算

带式输送机系统空间分布的托辊轴承处于相同工作条件下，其可靠性、额定寿命L10和运行时间之间存在一定关系，它们之间的关系通过滚动轴承失效的累积分布函数FTC(t)表示为：

FTC(t)=1-RB(t)=1-exp[-0.105 3(LS(t)/L10,m)10/9]

(1)

式中：RB(t)为滚动轴承的可靠性，L10,m是滚动轴承的额定寿命，LS(t)为滚动轴承已经达到的运行时间，其表达式为：

(2)

如果煤炭生产量和带式输送机的输送带速度恒定不变，则式(2)可简化为：

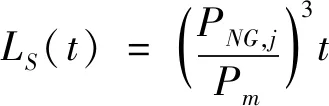
(3)

将误差项ε(t)引入到时间点ti-1和ti两次连续检查之间的故障率理论计算中，可以修正可靠性估计。引入误差项的修正故障率可以表示为：

(4)

在恒定的生产量和带速下，将式(1)代入式(4)，故障率可进一步写为：

(5)

3 决策算法

决策算法是带式输送机托辊维护决策框架的核心，其算法流程如图2所示。该算法将滚动轴承故障率的理论计算结果和实时监测数据作为输入，输出为失效的托辊和下一次检查时间。

图2 维护决策算法

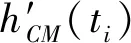
(6)

式中：TH(ti-1)表示在ti时刻超过阈值的轴承数量，fti(x)为监测参数的相对频率函数。

(7)

通过考虑两个故障率之间的差值∂(ti)，可以修正阈值TH(ti)。如果∂(ti)>0，则阈值在诊断时间ti+1可以修正为更高的值TH(ti+1)=TH(ti)+Θ。如果∂(ti)<0，则阈值在ti+1时刻修正为TH(ti+1)=TH(ti)-Θ。滚动轴承的诊断是通过一个不断更新的阈值来实现的。在时间ti检查后，通过检查监测参数值是否超过阈值TH(ti)来实现滚动轴承的诊断。

4 决策效果分析

采用模拟仿真和现场统计的托辊故障数据说明本文提出的带式输送机系统托辊维护决策架构的有效性。考虑到传感器的安装和可行性、信号的可解释性和及时性，选择温度作为托辊的状态监测参数。表1为带式输送机系统仿真实例中的相关参数设置。

表1 参数设置

模拟开始时，初始阈值设置为40 ℃。选择中心滚动轴承作为仿真研究对象。为了表示滚动轴承温度随时间的变化，随机分配10 002个中心滚动轴承的温度，使得它们的相对频率函数呈现如图3所示的模式。假设每次检验的模拟温度测量值服从正态分布。对于模拟研究，采用1个月的恒定检查间隔。对于框架中的误差项ε(ti)，考虑了一个线性模型ε(ti)=α1,i+α2,i·ti进行模拟。阈值增量Θ在仿真过程中设置为0.3 ℃。

图4所示为理论计算修正的故障率、具有更新阈值的监测数据故障率和应用L10轴承寿命理论得出的故障率随轴承运行时间的变化情况。由图4可知，前23个月L10理论的故障率最高。在此期间，温度的相对频率函数集中在低温区，这意味着很少有滚动轴承的温度超过阈值，故障率很低。23个月后，状态监测的故障率高于L10理论的故障率，同时状态监测的故障率发生了显著波动，这可归因于模拟温度测量值和阈值的同时变化。L10理论的故障率几乎恒定在0.2%，修正后的理论计算的故障率比状态监测的故障率变化更为平稳。从图4可以得出结论，在所提出的框架中理论计算修正得到的故障率比从L10理论得到的故障率更精确。

图3 轴承在不同使用时间的模拟温度分布

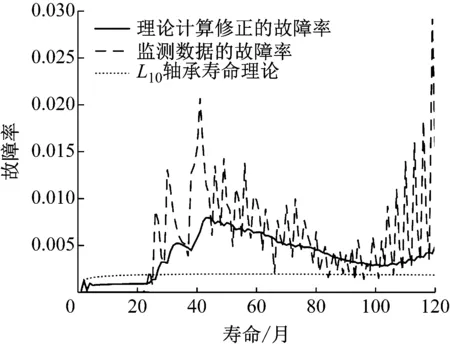
图4 仿真过程中滚动轴承的故障率

图5所示为模拟期间温度阈值随运行时间的变化情况。在前23个月阈值从最初的40 ℃线性下降到31.2 ℃，之后观察到阈值增加并在120个月结束于44.5 ℃。观察结果与模拟研究中预先设定的临界值40 ℃和托辊间的温度分布有关。前23个月很少有滚子轴承温度超过临界值，在这种情况下将阈值修改为较低的值。随着仿真时间的延长，滚柱轴承的温度超过临界值的次数多于可靠性计算指标，在此期间阈值将持续更新为更高值。图5表明可以用给定的初始值、实时数据和理论计算来更新阈值。

图6所示为分别采用本文方法、具有恒定阈值的传统方法和L10理论计算得到的滚动轴承故障累积分布。由图6可知，当托辊运行120个月时，利用本文提出的框架计算故障累计约为62%，说明10 a内将有62%的滚动轴承需要被更换。而L10理论计算结果表明只有22%的滚动轴承将被更换，恒温阈值的计算结果表明86个月后需要更换所有托辊。因此，综合维护决策框架能够为托辊故障提供更准确的决策。

图5 仿真过程中阈值的演化

图6 仿真过程中滚动轴承故障的累积变化

根据平煤集团某矿带式输送机系统近3年的现场故障数据统计，托辊的故障率为20%。基于经验常数阈值方法计算的托辊故障率为33%，而采用本文的综合维护决策架构计算的故障率仅为22%，与实际故障率更为接近。以上分析说明综合维护决策架构对托辊故障具有更强的预测能力，有利于矿井煤炭运输部门的管理。该架构在保证带式输送机系统可靠性的同时可降低维护成本。

5 结论

本文提出了一种基于带式输送机系统托辊的运行状态数据、可靠性理论估计和状态监测数据的综合维护决策框架。在此框架下，进行了可靠性理论估计与状态监测数据的交互作用，从而实现了托辊失效率预测的不断修正和阈值参数的进一步更新。该框架能够合理的对设备进行维护，可以帮助企业降低维修成本，具有较好的工程应用价值。通过仿真验证了该框架的有效性。现场故障数据统计结果表明，该框架能提高托辊故障的可预测性。