基于F-K滑移流模型的柱面微槽气浮密封浮升能力分析

2021-08-31陆俊杰张炜马浩

化工学报 2021年8期

陆俊杰，张炜，马浩

（1浙江大学宁波理工学院机械与能源工程学院，浙江宁波 315010；2哈尔滨商业大学轻工学院，黑龙江哈尔滨 150028）

引言

环形密封作为高参数旋转动力机械领域关键基础零部件，其性能优劣与机械设备的可靠运行息息相关。随着我国动力机械的功率和能量密度大幅提高，进而对密封系统提出了高转速、微泄漏、易维护和紧凑结构等苛刻要求。与此同时，美国宇航局NASA指出环形气膜密封可增加发动机9.7%的净推力，提升4.2%的效率并降低2.5%耗油率[1-2]，因此柱面气膜密封必将成为下一阶段重点研发对象[3]。

由于气体黏度较低，导致大间隙不利于气膜产生明显的流体动压效应，因此，通常情况下柱面密封的气膜厚度设置为3～9μm。但是在如此小的气膜厚度下，考虑到高空超速飞行的影响，柱面密封的气体滑移效应将会凸显出来。目前，对非无滑移流体机制的研究主要通过两种方法：一种是基于分子模型运动理论的分子动力学，以DSMC方法(direct simulation Monte-Carlo)[4-8]为代表；另一种是微流体力学，该方法以宏观流体状态方程为基础，利用各种微观效应对其进行修正。由于第一种方法所采用的复杂统计计算要求较高的计算能力，只有在先进的超级计算机上才能实现，具有很大的局限性。针对后者考虑气体滑移流效应和薄膜润滑理论的相关研究中，Burgdorfer[9]基于一阶滑移速度边界修正的Reynolds方程，首次分析了分子平均自由程对动压气体轴承性能的影响。在后续研究中各国学者发展了多种不同的滑移速度边界，包括Hsia等[10]提出二阶滑移速度边界、Mitsuya[11]在Hsia等提出的二阶滑移速度边界基础上进行修正，提出了1.5阶滑移速度边界；随后，Bahukudumbi等[12]给出了半解析模型，但是适用范围有限，求解过程较为烦琐。Fukui等[13]从Boltzmann方程入手，建立了Bhatnagar-Gross-Krook计算模型，研究结果证明该模型适用于任意Knudsen数下气体滑移流性能分析，并对后续各国学者研宄产生重要影响。但是上述模型中，Poiseuille流量系数的计算非常复杂，黄平[14]拟合了宽流域中模型计算结果，给出了计算Poiseuille流量系数的解析公式。基于大量气体稀薄效应的建模，Gu等[15]提出了一种结合了多种滑移模型和润滑理论的雷诺方程。

针对气浮密封稀薄效应引起气体滑移流现象，国内外专家学者大量研究工作侧重于通过密封支撑和表面结构，从而提高浮升力。Yamakiri等[16]对表面微结构的理论进行了研究，并证实表面微结构是一种非常有效的提高动压效应的方法。研究结果说明表面微结构可以储存润滑气体或液体；在小间隙下条形槽与点阵槽对其浮升力的提高更加明显[17]。Kovalchenko等[18]利用激光加工出不同类型的槽，发现槽内的动压效应将产生一个额外的托举力。尽管有限元法和有限体积法被广泛地应用于求解柱面气浮密封表面刻槽的润滑特性，但是其求解过程较为复杂[19]。因此，国内外学者倾向采用有限差分法进行求解，不仅离散简单而且求解效率高，如黄平[14]给出了不同类型动压润滑计算问题的有限差分格式。Childs等[20]采用有限差分法对火箭涡轮泵用浮环密封的静、动态特性进行了研究。Nagai等[21-22]利用五点差分法对航空涡轮泵中具有螺旋槽的液体环形密封件静态与动态特性进行分析。Zhang等[23-25]综合考虑气体滑移流效应和表面微结构，利用有限差分法用于热弹润滑仿真，详述了气膜压力、气体浮升力以及温度分布等。

从上述研究可以看出，由于柱面气浮密封的气体可压缩性特点，表面微槽不但影响动压效应，而且也会影响气膜偏心下的楔形效应，同时，槽型的动压效应又会对气体滑移流效应产生干扰，因此将表面微结构、偏心与气体滑移流机制三者有效结合，更能贴近柱面微槽气浮密封的服役环境，甚者上述三因素协同也会对该密封浮升力产生愈发明显的影响。本文提出新型柱面螺旋槽气浮密封，基于薄膜润滑理论，结合气体滑移流效应影响和表面螺旋槽结构特点，探讨了气体滑移流效应与运行参数的内在关联，并将计算结果与现有研究对比，揭示了柱面螺旋槽气浮密封滑移流效应与槽型参数的调控机制。

1 无滑移流与滑移流下的修正雷诺方程

1.1 几何模型

新型柱面螺旋槽气浮密封，如图1所示，其旋转环外曲面设有动压微槽，令浮环与旋转环之间的气膜因高速流动而产生动压，形成支撑浮环的浮升力，从而浮环与旋转环之间的间隙即为气膜厚度；同时，浮环存在偏心，使得气膜厚度呈楔形，由于挤压效应又进一步加强了气膜压力，提升了浮环的稳定。气膜间隙与槽深均为微米级，远小于其他结构尺寸。

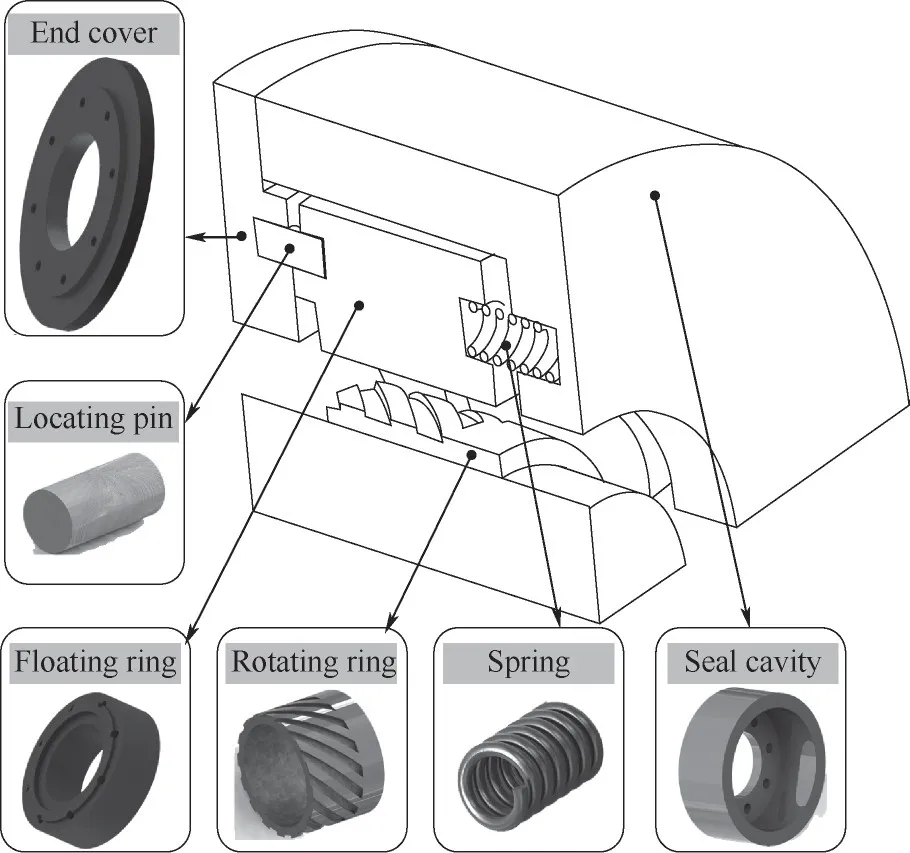
图1 新型柱面螺旋槽气浮密封结构图Fig.1 Schematic diagramof a new type of cylindrical spiral groove gas floating seal

1.2 流体控制模型

新型柱面螺旋槽气浮密封的气膜厚度只有微米级别，并考虑到流体速度与压力的关联，因而忽略膜厚方向的压力变化，其他假设如下：

(1)流体为牛顿流体，层流，且黏性力远大于体积力；

(2)膜厚方向不计压力和黏度变化；

(3)截面半径远大于膜厚，忽略气膜曲率的影响。

下文从无滑移流机制建立广义雷诺方程，以及考虑滑移流机制建立F-K滑移流模型。

1.2.1 无滑移流机制下雷诺方程新型柱面螺旋槽气浮密封物理模型如图2所示，O1是浮环的圆心，O2是旋转环的圆心，e是浮环圆心与旋转环圆心之间的距离，即为偏心距；运行过程中浮环与旋转环之间的径向间隙为气膜厚度，即h；由于新型柱面螺旋槽气浮密封存在偏心结构，因此浮环与旋转环之间的气膜厚度不均，其中hmin为气膜厚度最小区域，hmax是气膜厚度最大区域；浮环与旋转环的圆心不重合，α为浮环圆心与旋转环圆心连线和水平位置的夹角；θ是旋转环运行过程中的任意圆周角度。

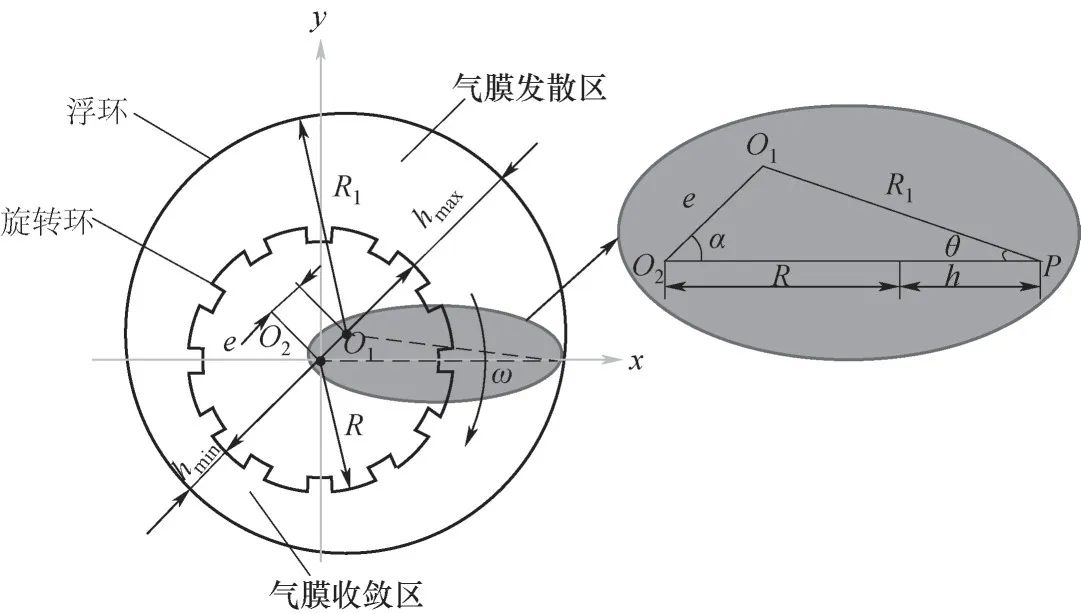
图2 新型柱面螺旋槽气浮密封物理模型Fig.2 Physical model of cylindrical spiral groove gas floating seal

根据前期研究和文献[26]，建立无滑移流机制下柱坐标雷诺方程

式中，z为无量纲轴向坐标，θ为圆周方向坐标，rad；R为旋转环的外半径，m；μg为润滑气体动力黏度，N·s/m2；ω为转轴转动角速度，rad/s；p为气体压力；h为运行过程中浮环与旋转环之间的径向间隙，即气膜厚度，m。

无量纲项：

式中，L为浮环密封轴长度，m；C为在运行前与无偏心情况下浮环内半径与旋转环外半径之间的差值，即初始气膜厚度，m；pa为环境压力(低压侧)，Pa;μ0为润滑气体环境黏度,N·s/m2。

浮环微槽密封的无量纲雷诺方程为

式中，Λx是可压缩系数。

1.2.2 F-K滑移流模型下修正雷诺方程

对于微间隙气体润滑，必须考虑滑移流效应的影响。考虑滑移流效应的无量纲Poiseuille流流量系数QMGL可表示

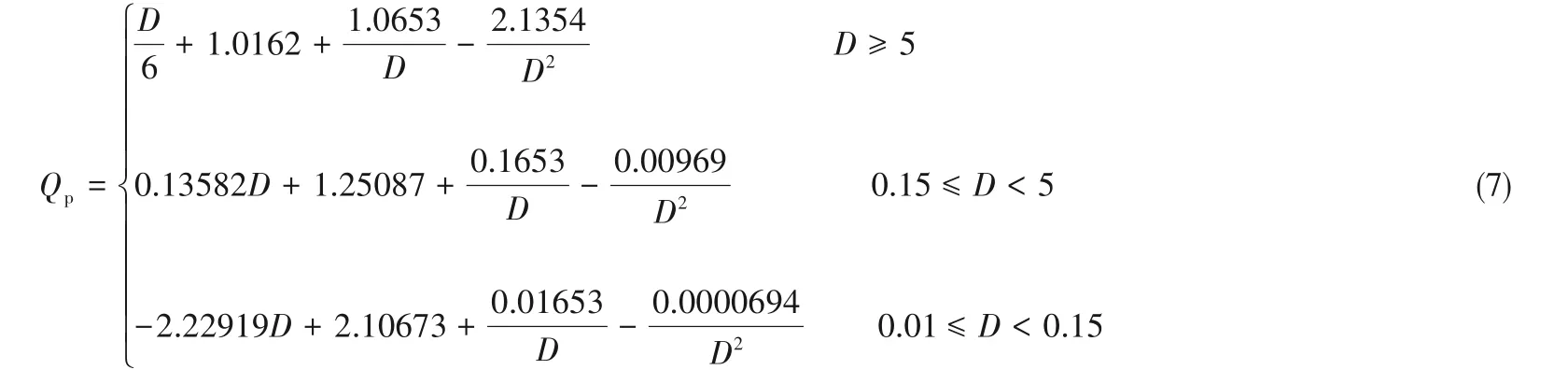
1.3 气膜厚度模型

根据图2中所示的气膜厚度几何模型结构发现：新型柱面螺旋槽气浮密封的气膜厚度h与圆周角θ、偏心距e以及旋转环表面的槽型结构存在联系。首先，对光面无槽的气膜厚度进行推导

式中，e为浮环圆心与旋转环圆心间的距离，即偏心距，m；α为浮环圆形与旋转环圆心连线和水平位置的夹角，rad；θ是旋转环运行过程中的任意圆周角度，rad；R1为浮环内半径，m。

由于e/R1<<1，cosα=1，由此得出

式中，C=R1-R为在运行前与无偏心情况下，浮环内半径与旋转环外半径之间的差值，即初始气膜厚度。

旋转环表面为有槽区与无槽区，气膜厚度分为两部分：①无槽处为光面无槽气膜厚度；②有槽处为无槽气膜厚度与槽深之和，如式(12)所示

根据式(2)，将气膜厚度h进行无量纲化

2 计算域离散与求解

新型柱面螺旋槽气浮密封具有偏心和微槽结构，并且密封轴向两端存在压差，因此气膜计算域需要进行整体划分网格；同时，由于Rayleigh台阶与楔形效应引发计算域中气体流量失恒与发散，因此文中采用八点差分法进行雷诺方程的离散与求解，如图3所示；另外，极薄的气膜厚度将引发较大的可压缩系数，从而可能导致计算发散，因此须采用迎风格式对其进行主元求解。

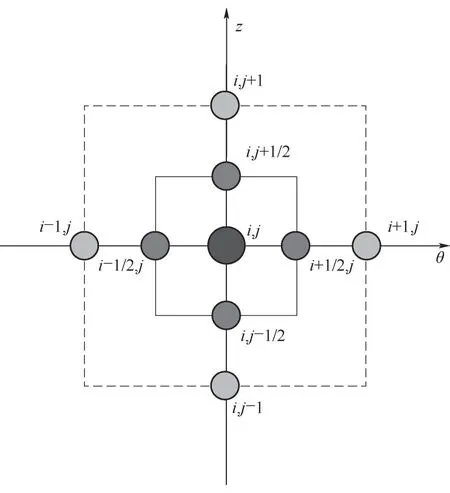
图3 八点差分节点示意图Fig.3 Schematic diagram of eight-point difference node

基于上述计算方法，F-K滑移流模型下修正雷诺方程式(5)的差分格式可写为

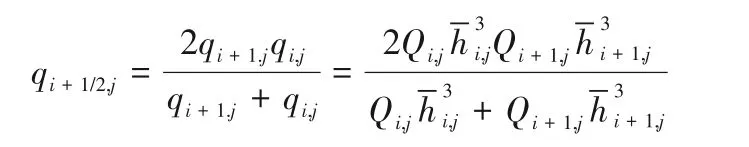
3 网格无关性与计算程序验证

3.1 边界条件

新型柱面螺旋槽气浮密封的压力场在周向上是连续的，θ方向为周向边界条件，对于雷诺方程，气体薄膜在密封端部分别与密封介质（高压侧）和环境（低压侧）相连通，即密封入口端的压力为密封介质压力，密封出口端的压力为环境压力。综上所述，边界条件为

气膜浮升力

3.2 迭代方法

采用超松弛迭代法求解，迭代格式为

在刚开始迭代时，由于误差较大，应使用较小的数值，取0.1；随着迭代次数的增加，相应增加至1。数值迭代计算过程中，按式（18）判断是否满足收敛条件

式中，err为误差收敛精度，取1×10-6；Ei,j为节点残差

式中，nr为转速，r/min；μ0为润滑气体环境黏度，N·s/m2；Δθ为周向节点；Δz为轴向节点；P1、P2、P3、P4和P5均为压力分量。

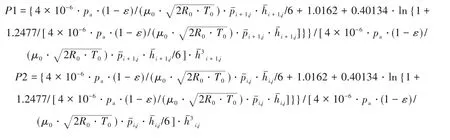
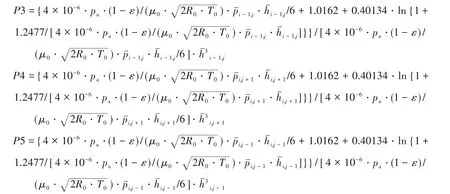
3.3 网格无关性验证

综合考虑密封轴向与周向差异，依次用8组不同的轴向与周向节点密度对计算域进行网格划分，分别为52×25、52×50、104×50、104×100、104×200、208×200、208×300、260×300个节点，并用不同密度的网格分别求解了耗时与计算较为复杂的F-K滑移流模型下修正雷诺方程，并计算了气膜浮升力，工况参数和螺旋槽结构参数如表1所示。气膜浮升力随网格密度的变化关系如图4所示，随着网格密度的增加，气膜浮升力的变化较为明显，总体上随着网格密度增加气膜浮升力上升，同时周向网格密度的影响大于轴向网格密封，从而也说明不连续槽台构成的Rayleigh台阶效应对计算精度有明显影响；当网格数量达到208×300时，结果几乎不再随网格数量变化。因误差建模过程中需进行上千次润滑计算，综合考虑精度和求解时间，选择208×200的网格进行后续的研究。

图4 网格无关性验证Fig.4 Grid independence verification

表1 柱面气浮密封工况参数和螺旋槽结构参数Table 1 Initial structural and operation parametersof spiral-grooved cylindrical gas-floating seal

3.4 计算程序与模型验证

为了验证本文计算结果的正确性，将文中无滑移流计算结果和F-K滑移流模型的计算结果与文献[27]的实验结果进行对比，文献中的转速为8000～38000 r/min，压力为0.1 MPa，计算参数如表2所示。

表2 文献［27］中的密封实验参数Table 2 The experimental parameters of Ref.［27］

图5所示为计算的结果与文献[27]的实验结果对比情况。由图可知，计算结果与实验结果近似程度很好，特别是F-K滑移流模型的计算结果与实验结果更为接近。这是由于柱面密封在小膜厚高转速情况运行时容易发生气体滑移效应，从而降低了气膜浮升力，导致无滑移流模型计算结果偏大，由此说明F-K滑移流模型较为准确。在8000 r/min时，F-K模型与参考文献的误差为9.52%；而在38000 r/min时，F-K模型与参考文献的误差为2.42%，说明在低速下，计算结果与实验结果误差较大，随着转速的提高，气膜流体速率不断提高，导致密封气膜滑移流效应愈发明显，因此与实验结果较为接近；在低转速下，由于动压效应不足，气膜稳定性较差，对实验测试也造成了一定的干扰，影响了数据的准确性。综上所述，从F-K模型与实验结果的对比分析说明，两者的趋势一致，且数值误差在合理范围之内，所以F-K模型具有一定的科学性。

图5 F-K滑移流模型计算结果与文献[27]实验结果的比较Fig.5 The comparison between the calculational result and experimental result of Ref.[27]

4 结果与讨论

根据表1的结构参数，首先对无滑移流与F-K滑移流模型下的气膜压力对比分析；然后基于工况、偏心、膜厚、槽深、槽数与槽长等因素，对无滑移流与滑移流的气膜浮升力进行深入分析。

4.1 无滑移流与F-K滑移流模型下的气膜压力对比分析

图6为无滑移流和F-K滑移流模型的气膜压力等高映射图，图中的纵坐标为无量纲气膜压力，横坐标为密封轴向与周向方向，其中周向方向以弧度值表示，展示了气膜压力在圆周（360°）的变化规律。从图6可以发现：柱面密封气膜压力在两种模型下都存在较大的压力波动，在圆周方向呈锯齿状分布，槽-台边缘处压力最大；在轴向，螺旋槽终止处的气膜压力最大。这种波动现象是由于旋转环表面螺旋槽具有泵送能力，它推动气流从槽内冲向槽台，发生阻塞流并形成台阶效应，从而产生压力突变；同时这种波动现象在高压区变得更为明显。这是因为高压区域的气膜厚度相对较小，螺旋槽所造成的气膜厚度变化率也相应变大，因此进一步影响了槽内气膜压力的变化量。

进一步对比图6(a)和图6(b)的压力变化趋势可以看到，考虑滑移流时，气膜压力在槽区和无槽区内都小于未考虑滑移影响时的气膜压力。由于滑移边界降低了浮动环与旋转环之间的相对速度，当气膜周向角度在180°（即π）附近时，气膜厚度最小，造成Knudsen数增大，引起滑移现象加剧，从而滑移流对压力影响达到最大；沿轴向在槽-台附近，螺旋槽增大了气体的压力梯度，从而提高了滑移流响应。

图6 无滑移流气膜压力(a)与F-K滑移流模型气膜压力(b)Fig.6 Pressures of gas film in the non-slipping flow model(a)and the F-K model(b)

综上所述：①滑移流降低了柱面螺旋槽密封的气膜压力；②螺旋槽内的动压效应由槽区阻塞效应和槽-台阶梯变化导致的动压楔和由偏心率导致的收敛楔共同引起。

4.2 不同工况下无滑移流与F-K滑移流的气膜浮升力

图7给出了柱面气膜密封的气膜厚度4μm、偏心率0.5时，不同密封压力下气膜浮升力随转速的变化规律。观察图中的趋势得知：气膜浮升力随着转速的升高而增大，但是在转速10000～50000 r/min和压力0.3～0.9 MPa下，无滑移流气膜浮升力始终大于考虑滑移流的气膜浮升力，如密封压力在0.3 MPa和转速10000 r/min时，无滑移流模型获得的气膜浮升力为618.80 N，F-K滑移流模型的气膜浮升力为594.99 N；而在0.3 MPa和50000 r/min时，无滑移流模型获得的气膜浮升力为1334.28 N，F-K滑移流模型的气膜浮升力为1158.14 N。在10000～50000 r/min，由于滑移流的作用，导致润滑气体的速度梯度有所减小，流体动压效果变弱，因而柱面螺旋槽气浮密封的浮升力减小；转速增大时，由滑移效应的润滑气体速度分量变大，从而说明了高转速可以增强滑移流效应。进一步观察发现：在0.3 MPa时，FK滑移流与无滑移流模型的气膜浮升力差值要明显大于0.9 MPa下两者气膜浮升力的差值，这是由于在低压低速下，动压效果差，使得气膜厚度较薄，其气膜剪切率较高，呈现较强的非线性特征，导致二者模型的计算误差较为明显，该推论也从文献[12,28]中得到了验证。

图7 无滑移流与F-K滑移流模型在气膜厚度4μm和偏心率0.5下气膜浮升力随转速和压力的变化规律Fig.7 Variationsof the floatingforces of the gas film with rotating speed and pressure in the non-slipping flow model and the F-K model under gas filmthickness 4μm and eccentricity 0.5

4.3 偏心与膜厚对无滑移流与F-K滑移流的气膜浮升力影响

图8给出了转速50000 r/min、压力0.3 MPa时，在不同气膜厚度下的气膜浮升力随偏心率的变化规律。由图可知，大偏心率对应高浮升力，这是因为浮环和旋转环之间构成的锲形随偏心率的增大而变得更明显，从而导致气体动压效应增强并提高了柱面气膜密封的浮升力。进一步观察发现，在气膜厚度较小时，无滑移流模型与F-K滑移流模型的气膜浮升力存在明显的差距，并且随着偏心率的增加导致有无滑移流效应下气膜浮升力的差距更明显，例如在气膜厚度为4μm、偏心率0.3时，无滑移流模型的气膜浮升力为708.65 N，F-K滑移流模型为607.47 N；在气膜厚度为4μm，偏心率0.8时，无滑移流下的浮升力为3568.42 N，F-K滑移流模型的浮升力为3068.86 N，该特点与文献[29]一致，说明F-K滑移流模型的准确性以及小膜厚下柱面螺旋槽气封发生了滑移现象。但是，随着气膜厚度的增加，不同滑移模型下获得的气膜浮升力之间差距越来越小，例如气膜厚度在4μm、偏心率为0.9时，无滑移流模型与F-K滑移流模型的气膜浮升力相差高达14.4%；气膜厚度在8μm、偏心率为0.9时，无滑移流模型与F-K滑移流模型的气膜浮升力相差仅6.5%。从而说明在气膜处于滑移流状态下，气膜厚度越小，滑移流影响越大；同时偏心率越高，导致气膜厚度分布更加不均匀，从而造成气体流速变化率更为明显，又进一步提高了滑移流对气膜浮升力的影响。

图8 无滑移流与F-K滑移流模型的气膜浮升力随膜厚与偏心率的变化规律Fig.8 Variations of the floating forces of the gas filmwith eccentricity and gas filmthickness in the non-slipping flow model and the F-K model

4.4 槽型参数对无滑移流与F-K滑移流模型的气膜浮升力影响

4.4.1 槽深图9为无滑移流模型与F-K滑移流模型在槽深2～32μm下的气膜浮升力变化趋势。从图中看到，槽深对柱面螺旋槽气浮密封的影响较为敏感。根据图6的分析可知,柱面螺旋槽气浮密封的动压效应由槽区阻塞效应和槽-台阶梯变化导致的动压楔和由偏心率导致的收敛楔共同引起；同时由于气膜为微尺度间隙，槽深的微弱变化均会导致气膜厚度在密封周向和轴向发生不同程度的改变，从而直接影响气膜浮升力的波动。非滑移流获得的气膜浮升力始终大于F-K滑移流模型，从槽深2～18 μm过程中，无滑移流模型与F-K滑移流模型的气膜浮升力随着槽深的增加而增大，且无滑移流模型与F-K滑移流模型间的气膜浮升力差值不断增大，这是由于槽深的增加使得槽区内气膜厚度相应增大，导致密封表面在周向和轴向的气膜厚度变化率相应变大，从而进一步提供了槽内气体的泵送能力和气膜压力的变化量，导致压力沿轴向的梯度p/z和周向的梯度p/θ增大，造成滑移流响应增强；但是在槽深18～32μm过程中，由于受到气体黏度的限制以及较大的槽-台阶梯深度引起的压力阶跃，考虑无滑移流机制的柱面螺旋槽气浮密封浮升力无法继续随着槽深的增加而增大；由于膜厚与Knudsen数之间的关系，随着槽深增加引发滑移流状态逐步转变为无滑移流状态，考虑到无滑移流机制下的气体不存在滑移边界，以及气膜流速更不会因为滑移流边界而削弱，因此随着槽深的进一步增加，当气体滑移流机制转变为无滑移流后，F-K滑移流模型下的气膜浮升力还会进一步增大；同时，从图9中发现，F-K滑移流模型下的气膜浮升力在后段上升速率已经远低于前段的上升速率，说明过大的槽深会影响气膜浮升力，极有可能槽深超过34μm后，F-K滑移流模型的气膜浮升力也会逐渐降低。

图9 无滑移流与F-K滑移流模型的气膜浮升力随槽深的变化规律Fig.9 Variations of the floating forces with the groove depth in the non-slipping flow model and the F-K model

4.4.2 槽数图10为无滑移流模型与F-K滑移流模型在槽数4～36下的气膜浮升力变化。从图中看到，气膜浮升力呈现抛物线趋势，说明存在极值。在槽数14下无滑移流模型和F-K滑移流模型获取的气膜浮升力都处于最大值，同时，在槽数从4变化到36的过程中，无滑移流模型下的气膜浮升力始终保持较大，表明：①在小膜厚下，气体存在边界滑移，并且滑移流将会降低浮环与旋转环间的气体速度，从而削弱气膜浮升力；②槽数的增加将会加重气膜在周向和轴向的不连续性，引起更为明显的槽-台处压力阶跃，造成气膜浮升力进一步下降。

4.4.3 槽长图11为无滑移流模型与F-K滑移流模型在槽长5～50 mm(其中浮环长度为52 mm)下的气膜浮升力变化。从图中看到，气膜浮升力呈现抛物线趋势，在槽长为5和50 mm时无滑移流模型和F-K滑移流模型的气膜浮升力相同；在槽长为30 mm下无滑移流模型和F-K滑移流模型获取的气膜浮升力都处于最大值；同时，槽长从5～50μm的整体变化过程中，无滑移流模型下的气膜浮升力始终较大且与F-K滑移流模型的气膜浮升力差值先增大后减小，表明：①槽长的增加，导致螺旋槽的泵送能力增强，并且有利于润滑气体在密封槽区聚集，进一步提高阻塞效应和槽-台处的压力突变，从而增加了气膜浮升力；与此同时，槽长的增加引起槽内动压效应提高，加强了槽内滑移流的响应，从而进一步削弱了气膜浮升力；②当槽长超过30 mm后，槽长比（螺旋槽的轴向长度与旋转环轴向长度之比）已经达到了58%以上，槽长的比例已经超过了旋转环的一半，造成气膜在轴向厚度明显变大，从而导致了润滑气体在槽内逐渐膨胀，降低了气膜浮升力；③当槽长比小于10%(槽长小于5 mm)和槽长比大于90%(槽长大于50 mm)后，滑移效应可以忽略不计。

图11 无滑移流与F-K滑移流模型的气膜浮升力随槽长的变化规律Fig.11 Variations of the floating forces of the gas filmwith the groove length in the non-slipping flow model and the F-K model