竖直多孔平板上液膜流动特性的研究

2021-08-31朱业铭刘金平许雄文朱丹丹

化工学报 2021年8期

朱业铭，刘金平，2，许雄文，2，朱丹丹

（1华南理工大学电力学院，广东广州 510640；2广东省能源高效清洁利用重点实验室，广东广州 510640）

引言

填料塔是建筑空调、化工吸收精馏等生产运行过程中不可缺少的环节。填料作为填料塔的核心部件，其性能对提高填料塔运行生产效率具有决定性作用。因此填料的性能研究工作一直以来都受到国内外很多学者的重视。

目前的研究可以分为3种尺度：微尺度、中尺度和宏观尺度[1]。微尺度针对填料小单元研究其流动和传热传质机理；中尺度的研究涉及多块填料板之间气液相流动的耦合作用，对填料的压降、含液率分布、分离效率、传热传质效率等进行集总参数研究[2-5]；宏观尺度则在中尺度的基础上，将填料塔作为一个整体来进行评估[6]。已有的研究表明，液相流动形态的改变通常只发生在几英寸(1 in=0.0254 m)大小的填料表面上，因此，大多数学者会将其简化为光滑平板或波纹板上的流动，在微尺度下利用CFD方法和厘米级别的计算域来研究填料小单元内的流动特性和传质性能[7]。其中，流动特性主要包括液膜覆盖率和波动特性。液膜覆盖率表征了气液接触面积，而液膜的流动形态对其有决定性作用。液膜的流动形态可分为薄膜流、溪流和滴状流。薄膜流具有最大的气液接触面积，是最理想化的流动形态，有利于传热传质过程[8-10]。但在实际过程中，流动形态受到很多因素的影响，比如流道结构、流体物性、气相流速、液体流速等[1,11-14]，控制和产生薄膜流态非常困难。另外，流动波动特性也会破坏膜状流态。目前对于波动特性的研究主要集中在厚度分布、速度分布和涡流上。厚度分布能够反映液膜波动和流动结构，速度分布、涡流与传质息息相关[15-18]。进一步分析其流动和传热传质机理，则需考虑到气液逆流的曳力作用和相间传热传质机制[19-21]。

虽然填料性能的研究已经非常丰富，但目前的研究主要着眼于平壁液膜，孔板上降膜流动的研究还较少。然而在工业中，许多类型的填料都有开孔[22]。研究表明，孔结构能够影响液体扩散和重新分布，使液膜分布更均匀，填料液膜覆盖率和气液接触面积更大。Liu等[23]通过建立多尺度模型描述了多孔填料内液体的流动行为，认为开孔能够改变液体的流动方向，使更多的液体在填料中间聚集而不是形成沟流，从而改善液体的分布。Subramanian等[24]建立了三维VOF模型，讨论了开孔对波纹板润湿性的影响，结果显示低流量下的液体流动会更多地利用开孔来对板两侧进行润湿。另一方面，孔结构对传质也有强化作用。Kolev等[25-26]的实验结果表明在相同的比表面积下，穿孔板具有更高的传质能力。Hu等[27]开发了一种新型开孔填料，并将其应用于二乙醇胺溶液吸收二氧化碳，在低黏度和高黏度条件下，传质系数可分别提高30%～40%和60%～70%。同样的填料被用于从水中解吸氧气，传质系数可提高35%～45%[28]。二维VOF模型也被用来证明这一现象。Zhu等[22]报道孔板的传质速率比光板提高了10%～20%。Hu等[29-30]发现孔内和下壁区域的平均传质系数比上壁区域分别提高了26.9%和17.4%。

尽管研究指出孔结构能够改善液体分布和传质效率，但孔对液体扩散的影响机理还不清楚，孔的干燥态和润湿态对液膜铺展的影响尚不明确；液膜波动特性一定程度上能够反映传质特性，但目前尚无文献对孔板上液膜波动程度、气液流场的作用进行分析。本文针对这些问题，采用三维数值模拟和实验相结合的方法，对竖直光滑和多孔平板上的液膜流动展开研究，分析孔结构对液膜铺展及液膜波动特性的影响。

1 数值模型

1.1 计算域及仿真条件

本文针对填料小单元进行分析，数值模拟的计算域是基于一个垂直的铝板，代表几英寸大小的填料表面。采用了两种流体域，一种光板，一种多孔板。图1(a)为光板的计算域和几何尺寸示意图，整个宽度方向被定义为入口。对于多孔平板，两个液膜分别在板的两侧流动，然后在孔内聚集，最后被下壁分离，该过程在多孔板上不断循环。由于多孔板流动的对称性，参考文献[31]，在孔中间位置使用了对称边界条件。多孔板计算域及几何尺寸如图1(b)、(c)所示。

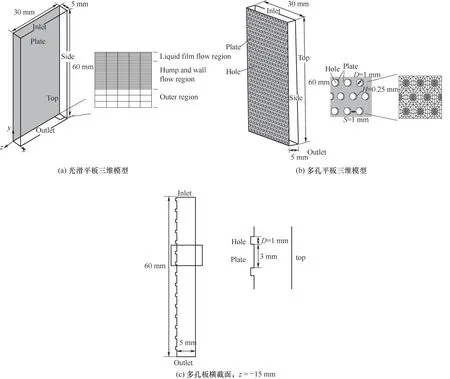
图1 计算域示意图Fig.1 Schematic diagramof calculation domain

为了准确高效地捕捉液膜流动形态，整体采用结构化六面体网格对计算域进行离散，孔结构区域采用Oblock方法进行网格划分[图1(a)、(b)]。考虑到网格数量，x方向上的网格采用了3种密度分布[图1(a)]。本文主要研究液膜流动特性，因此封闭膜流区域(x<0.5 mm)网格最密；而对于溪流区域，液膜收缩会出现一个最大股峰，股峰与壁流的液膜厚度较大，因此股峰与壁流区域(0.5 mm2.0 mm)，几乎没有液相的存在，因此网格最稀疏。

表1给出了模型的边界条件。考虑到计算域的流动长度较短，入口采用Nusselt理论的速度分布，入口液膜厚度和速度分布均跟随Re变化而变化，气液相率分布随入口液膜厚度变化而变化。

表1 模型边界条件Table 1 Model boundary conditions

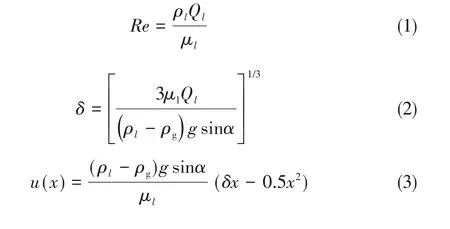
式中，α为平板倾角，取α=90°，空气与水作为两相系统流体，接触角设置为70°。流体流率Ql取值范围为3.8×10-5m2/s≤Ql≤3×10-4m2/s，其对应的Re范围为37≤Re≤298。

本文研究的是液相液膜流动，且Re<300，因此可认为是层流流动。一般来说，研究液体流速对液膜覆盖率的影响有两种方式，一是增大液体流量，由滴状流发展为溪流，再发展为膜流；二是以高Re先形成膜流，再减小流量，出现液膜破裂形成溪流。因为要研究润湿与非润湿孔对液膜铺展的影响，因此模拟中采用增加液体流量的方法。为了得到润湿孔，孔中的计算域初始条件为全液体。

1.2 控制方程

本文采用Fluent求解器计算，选用几何重建格式的VOF模型来对气液两相流界面进行三维模拟。CFD控制方程主要包括质量守恒方程、动量守恒方程、能量守恒方程。由于并未考虑传热传质，所以能量守恒可以忽略，即可只考虑质量守恒和动量守恒方程，分别为：

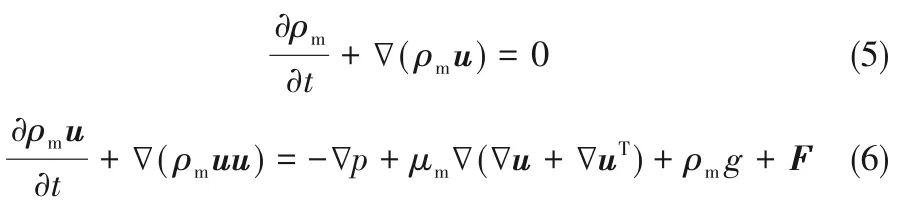
式中，F为除重力外的体积力，这里只考虑了表面张力，采用连续表面张力(CSF)模型计算。两相界面的跟踪是通过求解各计算单元中相分数（γl）的连续方程来实现的：

压力-速度耦合采用PISO方法，压力项采用PRESTO！方法进行差分，动量方程采用采用二阶迎风格式差分。光板计算时间步长在1×10-5～5×10-5之间调整，而孔板的计算时间步长在1×10-6～5×10-6之间，保证在整个计算过程中柯朗数在0.5以下。当液膜覆盖率和出口质量流量稳定时，认为模拟到达稳态。

2 实验设计

实验装置如图2所示，水从上水箱中流出，流经阀门、转子流量计和进料管，连接到实验板的顶部，在进料管和实验板之间缠绕纱布以改善初始液体分布。液体在板上扩散，然后进入下水箱进行再循环。转子流量计的测量范围为60～600 ml/min，覆盖了本实验的范围，并用称重法对其进行了校准。实验板为30 mm×60 mm的铝板，厚度为0.5 mm。表面不应有划痕与毛刺，以减小粗糙度和钉扎效应的影响。为了满足模拟中两侧壁面边界条件的设置，在实验板两侧设置铝板。水与实验板的接触角如图3所示。

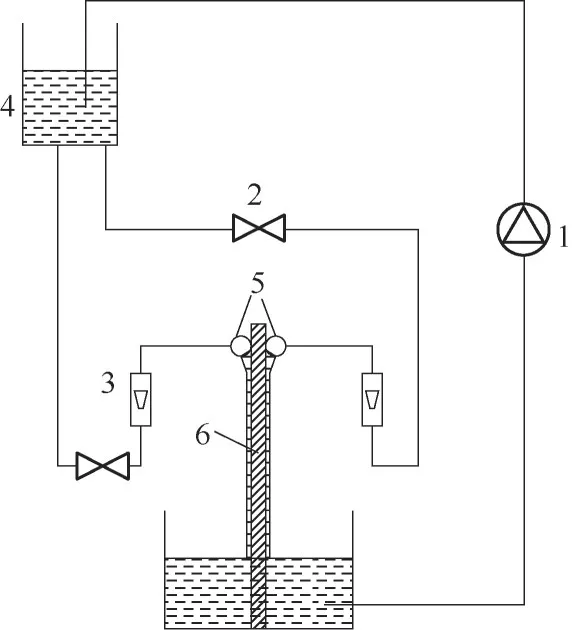
图2 实验装置示意图Fig.2 Experimental setup

图3 水与铝板的平衡接触角Fig.3 Equilibriumcontact angle between water and aluminium plate

实验板液膜覆盖率等于润湿面积Aw与平板总面积At之比:

实验中采用红外热像仪拍摄液膜流动图像，以捕捉竖直平板上的液膜分布。拍摄图像如图4所示，由于水与铝板的温度及表面发射率差异，红外热像仪对其感应温度不同，可清晰分辨出液膜与干斑区域。通过Photoshop识别润湿区域和平板区域的像素点个数，可以得到润湿区域的像素点比例从而测得液膜覆盖率。需要注意的是，在计算多孔板的液膜覆盖率时，没有考虑孤立的润湿孔，而只考虑了串连的液膜。

图4 红外热像仪成像示意图Fig.4 Photo by infrared thermal imager

3 结果讨论

3.1 网格独立性

为了检查网格独立性，液膜覆盖率和位于板宽中心、平板中下游某一点(z=-15 mm，y=20 mm)的稳态液膜厚度被作为独立性判据。表2为不同网格数下光板和多孔板模型的网格尺寸。图5(a)、(b)为不同网格数下光板和多孔板上液膜覆盖率与流动时间的关系，图5(c)、(d)为某特定点的液膜厚度与网格数的关系。综合考虑两个独立性判据结果的偏差以及运算时间，光板和多孔板的优化网格数分别为22.5万和143万。

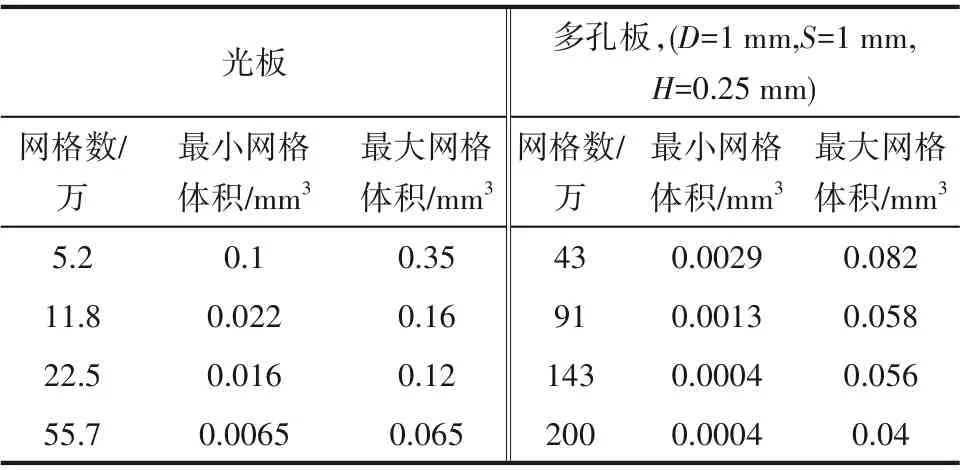
表2 光板和多孔板模型的网格尺寸Table 2 Mesh size of nonporous and porous plates

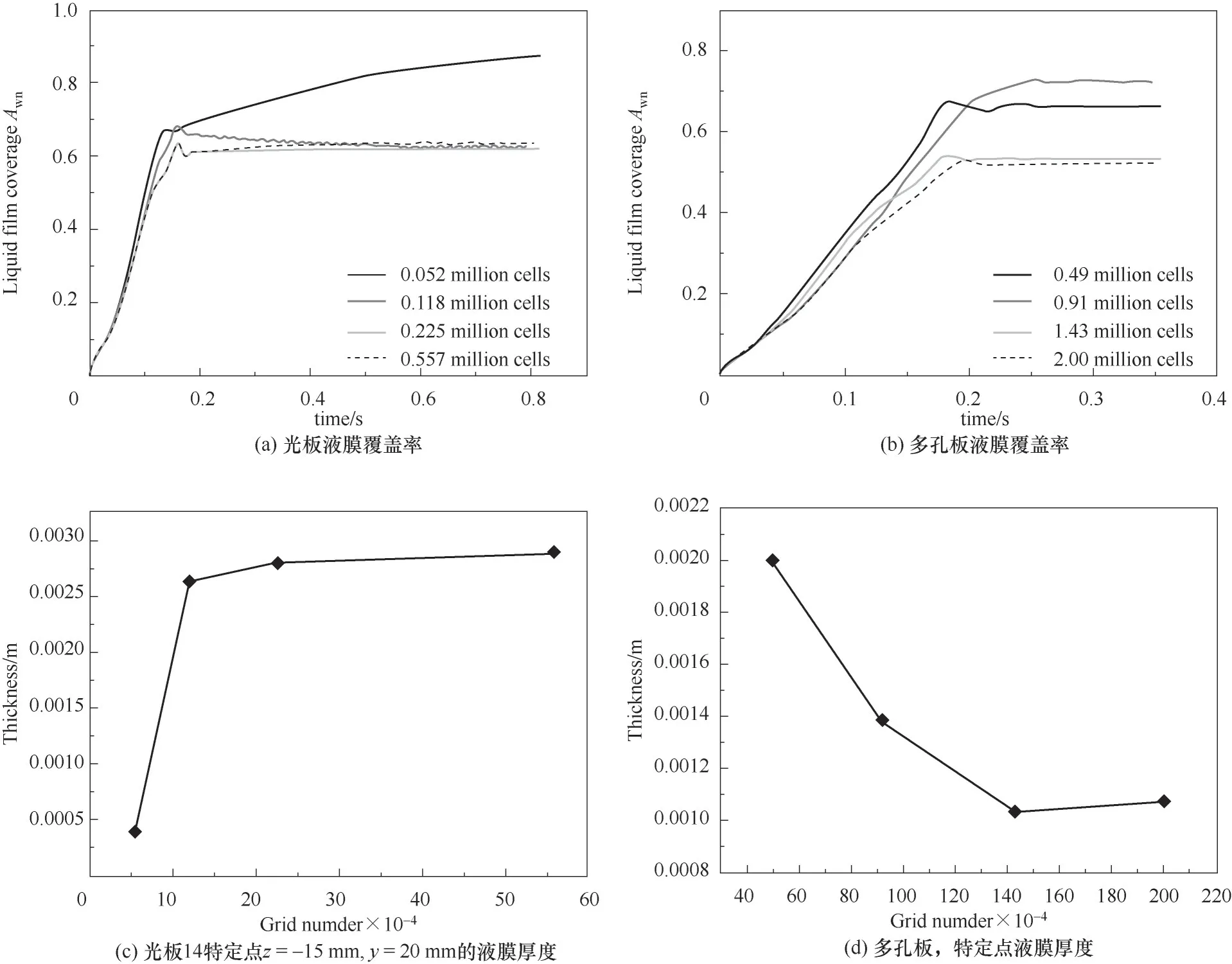
图5 网格独立性检查(D=1 mm，S=1 mm，H=0.25 mm)Fig.5 Grid independence

3.2 模型验证

为了验证模拟的合理性，将光板、1 mm润湿孔板的模拟结果与前人的模拟结果、实验结果进行了比较。如图6(a)、(b)所示，液膜覆盖率均吻合良好，三维流型也具有一致性。此外，Nusselt速度分布入口保证了光板板宽中心的速度与厚度关系始终能满足Nusselt理论。

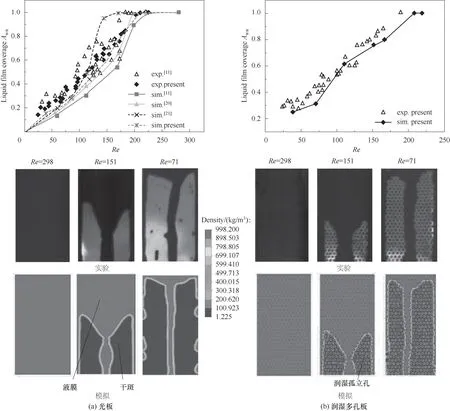
图6 实验与模拟液膜覆盖率的对比(D=1 mm，S=1 mm，H=0.25 mm)Fig.6 Comparison of wetted area between experiment and simulation

3.3 润湿孔和干燥孔对液膜覆盖率的影响

当液体在光滑平板上流动时，在表面张力的作用下会出现收缩。多孔板上的液体流动分为两种情况：干燥与润湿多孔板，二者区别在于初始状态孔内是否充满液体。图7为光板与多孔板上液膜覆盖率的比较。结果表明，除了在极低流量外，干燥多孔板上液膜覆盖率低于光板；而润湿多孔板上液膜覆盖率均高于光板。对于前者，孔是干燥的，孔内充满空气。孔边缘两侧的润湿性存在较大的差异，孔内相当于不润湿区，孔外为润湿区。此时，三相接触线会出现黏滞即钉扎效应，使液体倾向于沿孔外表面流动，而不是流经孔。当流量增大，液体与孔边缘的接触角θ也会不断增大，如果竖直方向上的重力和惯性力能够克服气液表面张力作用，液体就能够穿过孔继续向下流动。由于受到大量干燥孔的限制，液体流动区域受限，阻碍液膜的铺展，使液膜覆盖率降低。对于后者，孔是润湿的，孔内充满液体，孔边缘两侧的润湿性同样存在较大的差异。不同的是，此时孔内液体可视为接触角为0°的润湿区，而孔外相当于不润湿区。三相线可以在0°接触角的润湿区不受限制地移动，直至移动到对侧孔边缘出现黏滞。由于大量的润湿孔存在，减小了流动的限制，因此润湿多孔板能够促进液膜扩散，液膜覆盖率得到提升。并且由图8可以看出，三种不同Re下的流型基本保持一致，会存在滴状流、溪

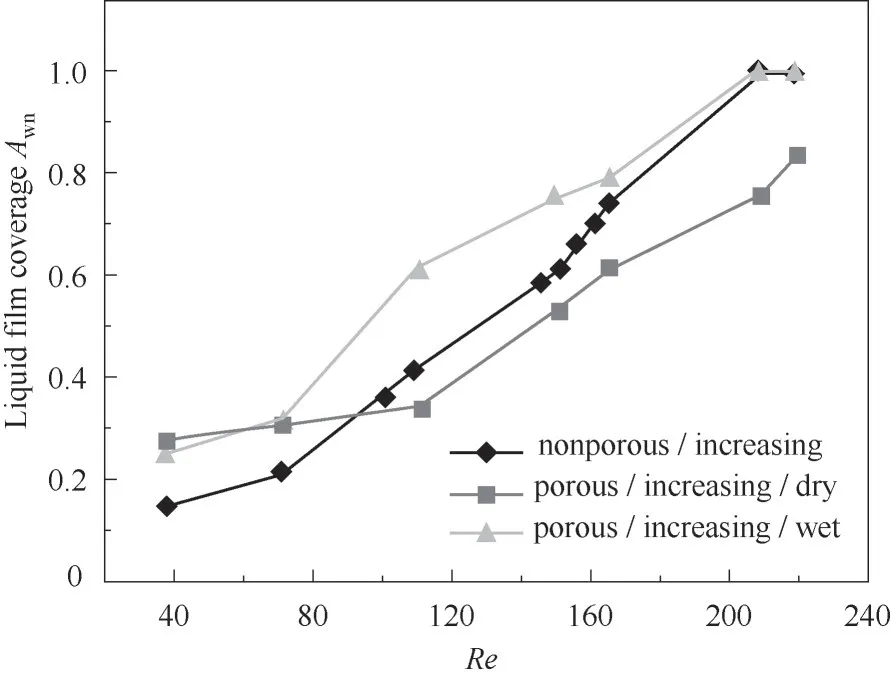
图7 光板与多孔板液膜覆盖率对比(D=1 mm，S=1 mm，H=0.25 mm)Fig.7 Comparison of liquid film coverage between smooth plate and porous plate

图8 光板与多孔板的流型对比(D=1 mm，S=1 mm，H=0.25 mm)Fig.8 Comparison of flow patterns between smooth plate and porous plate

另外，值得注意的是，不管是对光板还是润湿多孔板，在模拟中增大流量与减小流量两种工况下得到的液膜覆盖率是一致的。而在实验中，会出现减小流量下的润湿面积大于增大流量下的润湿面积。这是由于钉扎效应的作用，后退接触角小于前进接触角。并且对多孔板来说，由于润湿孔的存在，板上存在交替的润湿区(孔内)和不润湿区(孔外)，三相线的回缩可能会受到限制，进一步阻碍液膜的收缩。文献[31]通过单个液滴在盲孔基底上的流动实验也获得了相似的结论，向润湿孔移动的液滴被加速而远离润湿孔的液滴受到阻碍，但其未提及干燥孔的作用。

3.4 孔径对液膜波动特性的影响

为了研究孔径对液膜波动特性的影响，进行了高Re下的润湿孔模拟，以得到封闭的液膜。在本节中，孔间距保持为1 mm，孔深为0.5 mm，孔为叉排排流和膜状流三种流型，只是流型转变的Re与位置存在差别。列，仅改变孔径大小以研究孔径对液膜的影响。液膜厚度是反映液面波动的重要参数。图9展示了不同孔径下液膜的相界面，由图9(a)～(d)的封闭液膜可以看出，与光板相比，多孔板上的液膜出现明显的波轮廓，且随着孔径的增大，轮廓愈发明显。波的存在能够增强扰动，有利于传热传质。取板宽中心处的二维相界面分析，如图10(a)～(d)所示。光板及1 mm孔板上液膜相界面比较平整，2 mm孔板上有细微的起伏波出现，而4 mm孔板能够看到明显的液面起伏。孔径越大，厚度起伏波动越大。波数与孔的数量保持一致。其产生的原因是液膜由上壁面流入孔时，从受壁面约束转化为到无壁面约束状态，液膜有内凹趋势，厚度减小，出现波谷；液膜由孔内流入下壁面时，液体会对孔内壁进行撞击产生水平超调，厚度增大，出现波峰。另外可以看到，当D=4 mm时，平板中下游的孔中存在额外的毛细波，如图10(d)中区域Ⅰ～Ⅲ所示。这可能是液体对孔内的下壁面进行冲击产生的高滞止压力向上游传递造成的。

图9 不同孔径下的相界面(VOF=0.5，Re=298,S=1 mm，H=0.25 mm)Fig.9 Phase interfaces with different diameters

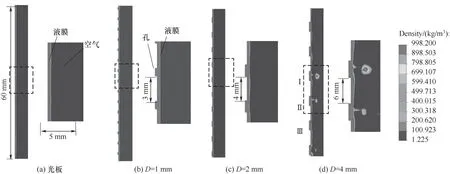
图10 不同孔径下的封闭液膜形态(z=-15 mm，Re=298，S=1 mm，H=0.25 mm)Fig.10 Closed filmmorphology with different diameters

此外，图11展示了该相界面的厚度分布，由图可以看出，随着孔径增大，液膜厚度的最小值会减小，最小值出现在孔内的某个位置。当液膜厚度等于0时，液膜就会破裂。这一定程度上能够解释为什么在大孔径下的液膜流动中，孔内液膜容易破裂的现象。图9(d)、(e)和图12分别为液体在4 mm和6 mm孔板上流动的模拟和实验结果。可以看到，D=4 mm时能够形成封闭的液膜，而D=6 mm时呈溪流状，这是由于4 mm孔能够始终保持润湿态，而6 mm孔孔内液膜会破裂，由润湿态变成了干燥态，阻碍了液膜的铺展。实验和模拟结果相吻合，这也证明了模拟的有效性。

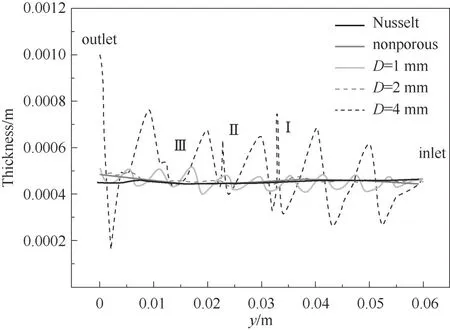
图11 不同孔径下的封闭液膜厚度分布(z=-15 mm，Re=298，S=1 mm，H=0.25 mm)Fig.11 Closed filmthickness distribution with different diameters

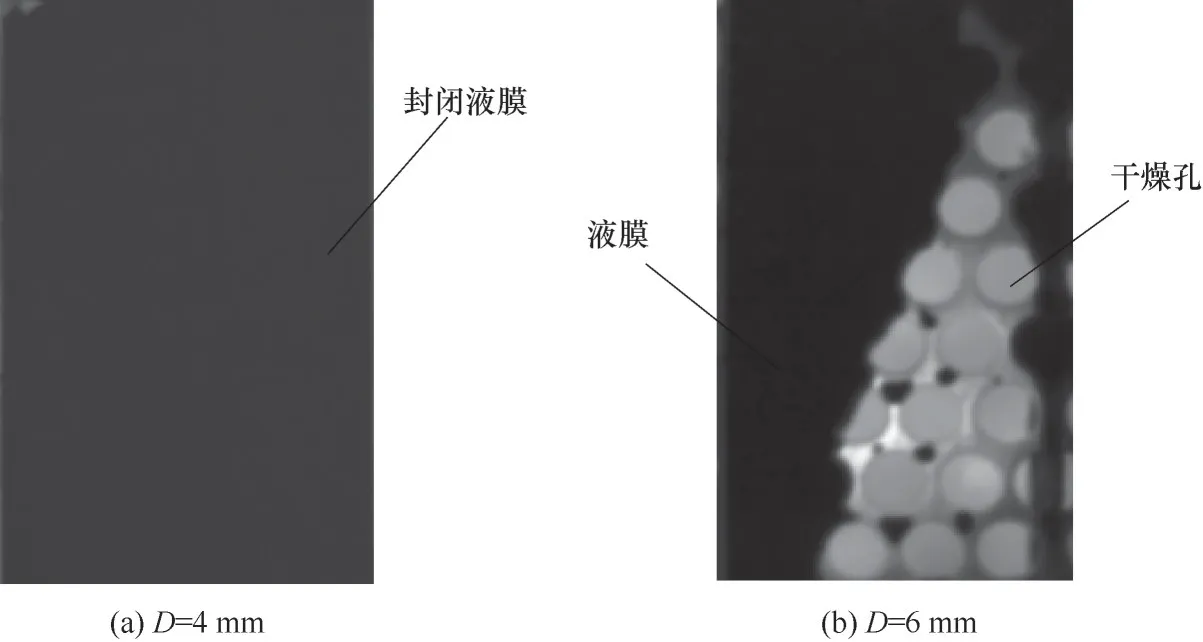
图12 不同孔径下的液膜流动形态实验（Re=298，S=1 mm，H=0.25 mm）Fig.12 Experiments of liquid film flow pattern with different diameter

但是液膜的瞬时厚度是受孔径、孔深、孔间距、多孔的排列方式、液体流量、流动形态等因素影响的，而这些因素是相互耦合的，本文只是针对某一特定情况进行了分析讨论，更加系统的评估会在以后工作中进行。可以预见的是，孔板的厚度越大，孔深也越大，孔内液膜会越难破裂，有利于液膜的铺展。

沿厚度方向上的速度分布(x方向速度)与传质方向一致，增大该速度能够增强传质效果。从图13(a)可以看出，液膜在光板和1 mm孔板上流动时，x方向速度几乎为0，不利于传质。随着孔径的增大，2 mm孔板上x方向速度出现了一定程度上的波动，波数与厚度波动的波数一致。4 mm孔板上的波动更加剧烈，特别是对于存在毛细波的区域Ⅰ～Ⅲ，数值上有很大的提高，有利于传质。波动是液体对孔下壁进行冲击产生的水平超调引起的，孔径越大，冲击越强，波动也就越剧烈。沿流动方向上的速度可以反映液体在平板上的流动时间。从图13(b)可以看出，4 mm孔板上的液膜y方向竖直向下的流动速度在中下游有明显的减小，在毛细波的区域Ⅰ和Ⅱ，y方向流动速度有大幅度的缩减。这说明孔结构能够延长液体在平板上流动的时间，强化传热传质。

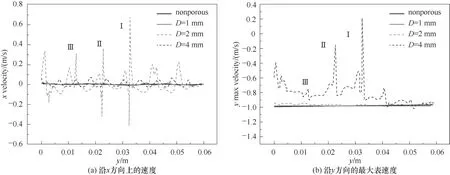
图13 封闭液膜速度分布(z=-15 mm，Re=298，S=1 mm，H=0.25 mm)Fig.13 Velocity distribution of closed film

图14为不同孔径下板宽中心的流线分布。相较于光滑平板，多孔板上的孔内区域会存在涡旋，能够促进液膜内部的液体进行交换，使液膜内部状态趋于一致，对传质会有一定的增强效果。另外，如图14(a)～(c)所示，光板、1 mm、2 mm孔板气侧流线整体呈现为一大尺度涡，而后两者由于孔的存在，会存在额外的小尺度涡。随着孔径的增大，由于4 mm孔板上液膜表面出现毛细波，气侧会被毛细波分割成几个较大尺度的涡，涡结构变得较为复杂，如图14(d)所示。涡结构能够增大气侧扰动，有利于传质。

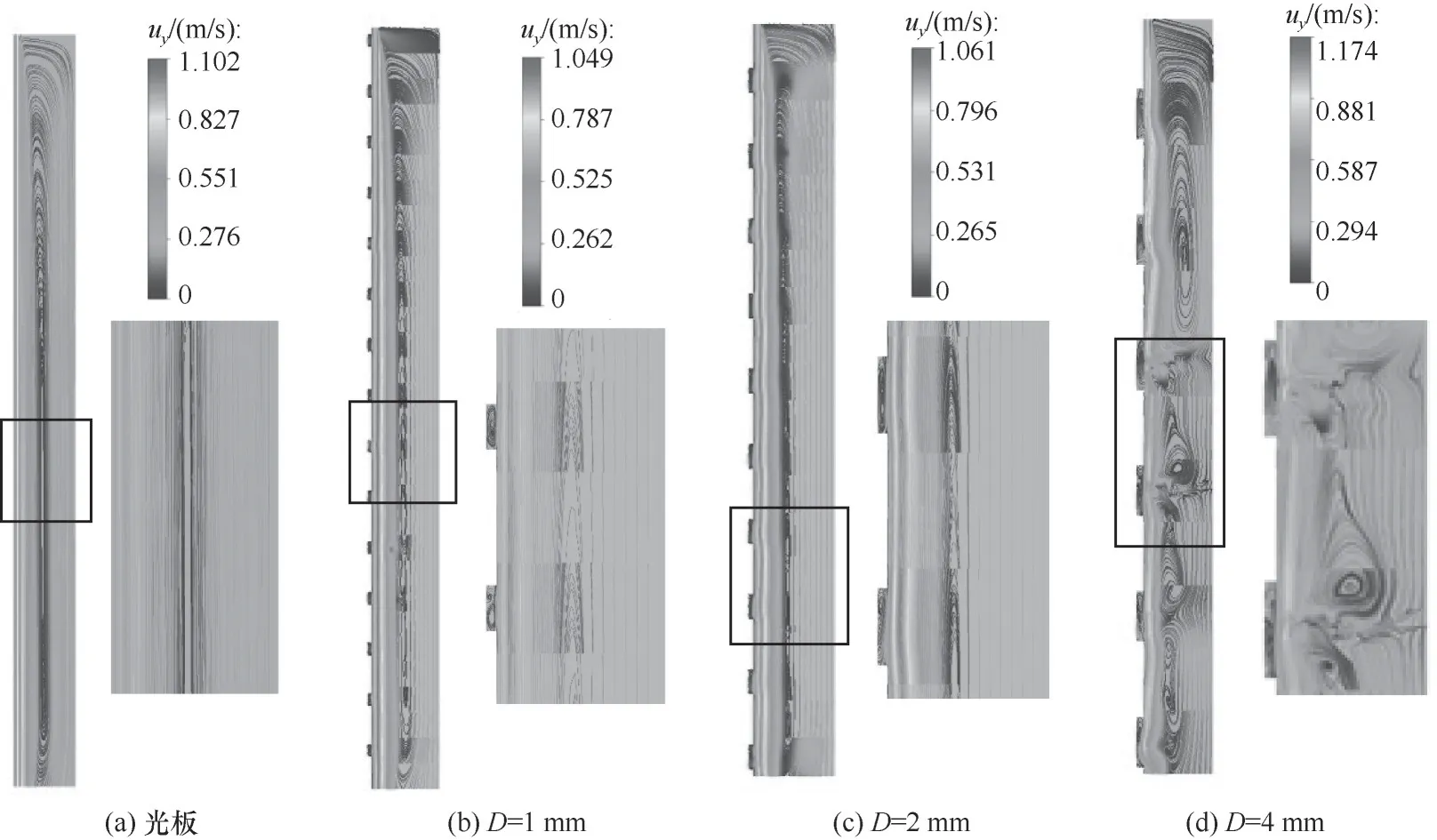
图14 封闭液膜流线(z=-15 mm，Re=298，S=1 mm，H=0.25 mm)Fig.14 Streamline of closed film

4 结论

本文建立了三维光滑平板和多孔平板上液膜流动的数值模型，并实验验证了数值计算模型的准确性。通过对模型和实验结果的分析，得到如下主要结论。

(1)干燥孔会阻碍液膜铺展，减小液膜覆盖率；而润湿孔具有促进液膜铺展、阻碍液膜收缩的双重作用，能够提高液膜覆盖率。

(2)孔结构能够使液膜厚度产生波动，多孔板上有明显的起伏波存在，且孔径越大，起伏波越剧烈。当孔径增大到一定程度，孔内会出现额外的毛细波。孔深0.5 mm时，4 mm孔径下会出现毛细波。但随着孔径的增大，液膜的最小厚度会降低。当孔径增大到一临界值使得液膜厚度为0，液膜会破裂。孔深0.5 mm时，4 mm及其以下孔径能够形成封闭液膜，而6 mm及其以上液膜会破裂呈溪流状。

(3)液体对孔下壁面的冲击会产生水平超调。多孔板上存在沿厚度方向上的速度及其波动，且其随着孔径的增大而增大。孔内的毛细波对其有大幅度的增强效果。竖直流动方向上的最大表速度随着孔径的增大而减小，毛细波对其有明显的削弱作用。

(4)孔内区域存在涡旋，能够促进液体交换；气侧涡旋结构随着孔径的增大而变得复杂，毛细波对其有分割作用。

符号说明

At——平板总面积，m2

Aw——润湿面积，m2

Awn——液膜覆盖率

D——孔径，m

F——源项

g——重力加速度，m/s2

H——1/2孔深，m

p——压力，Pa

Ql——单位宽度的体积流量，m2/s