基于自适应免疫-最小一乘算法的生物电阻抗特征参数提取

黄经纬，曹乐，阚秀，李敏

上海工程技术大学电子电气工程学院，上海201620

前言

生物阻抗特性是指生物组织的电学参数（电阻值和电容值）随着加载激励电信号频率的变化而发生显著变化［1］。近年来生物电阻抗技术发展迅速，目前已广泛应用于早期疾病诊断、生物组织液检测和生理状态评估等领域［2-5］。为了更好地研究生物阻抗，Cole等［6-7］建立了生物阻抗特征方程，即Cole-Cole方程，并提出4 个生物组织特征参数（Cole-Cole 参数）。随后，越来越多的研究者投入到提取Cole-Cole参数的工作中［8-11］，目前最常用的方式是通过拟合Cole-Cole 圆弧间接提取。Macdonald 等［12］首次将非线性最小二乘法（LS）用于Cole-Cole 参数的提取。Chen 等［13-14］采用Broyden-Fletcher-Goldfarb-Shanno（BFGS）方法降低了算法复杂度，同时利用最小一乘法（LAD）提取Cole-Cole参数，并与LS算法的提取结果进行对比，结果表明当含有多种误差数据时，LAD算法可以获得更为准确的Cole-Cole 参数。Gholami-Boroujeny 等［15］将细菌觅食算法（BFO）与LAD 算法结合，将参数拟合问题转化为参数值的组合问题，规避了BFGS 中近似Hessian 矩阵的求解，进一步简化了算法。受生物免疫系统的启发，免疫算法作为一种新型智能搜索算法被提出。近年来，免疫算法已广泛应用于非线性最优化、组合优化、控制工程、机器人、故障诊断、图形处理等诸多领域［16-20］。本文针对提取Cole-Cole参数提出了一种将最小一乘法与自适应免疫算法相结合的新方法，该方法具有结构简单、鲁棒性强、收敛速度快的特点。其中，自适应免疫算法在免疫算法的基础上设计了多种自适应算子，并通过借鉴遗传算法精英保留的思想，增设记忆单元，从而提高了算法的全局收敛速度、增强了局部寻优能力。为了验证本算法提取Cole-Cole参数的有效性和优越性，本文通过设定相应的评价指标，将自适应免疫-最小一乘算法与其他3 种算法进行对比分析。

1 模型建立与算法优化

1.1 Cole-Cole模型

生物细胞组织的电学特性可用图1所示的等效电路模型表示。其中，Re、Ri分别表示细胞外液电阻与细胞内液电阻，C表示细胞膜电容。

图1 生物细胞组织等效电路模型Fig.1 Biological tissue equivalent circuit model

基于生物细胞组织等效电路模型和Cole-Cole理论建立Cole-Cole方程：

其中，Z(ω)为生物复阻抗，ω为角频率，ω= 2πfc，fc为特征频率，即表示阻抗值最大时的电流频率，R∞、R0分别表示电流频率无穷大与电流频率为零时生物组织的电阻，α为散射系数（0 ＜α＜1），τ为弛豫时间。基于方程（1）得到Cole-Cole 参数：R∞、R0、α和τ（或fc）。其中，τ与fc具有以下关系：

基于Cole-Cole 理论，生物阻抗的轨迹可用一段分布在复平面第4 象限内的圆弧表示，即Cole-Cole圆弧，圆心坐标为如图2所示。

分析图2中几何关系，可得：

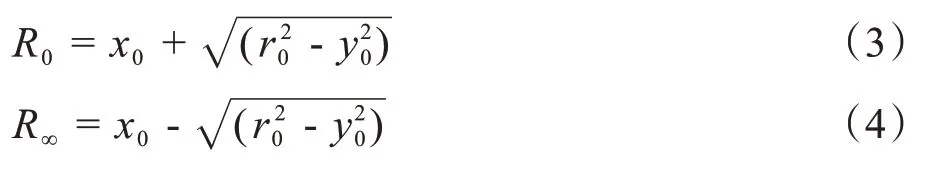
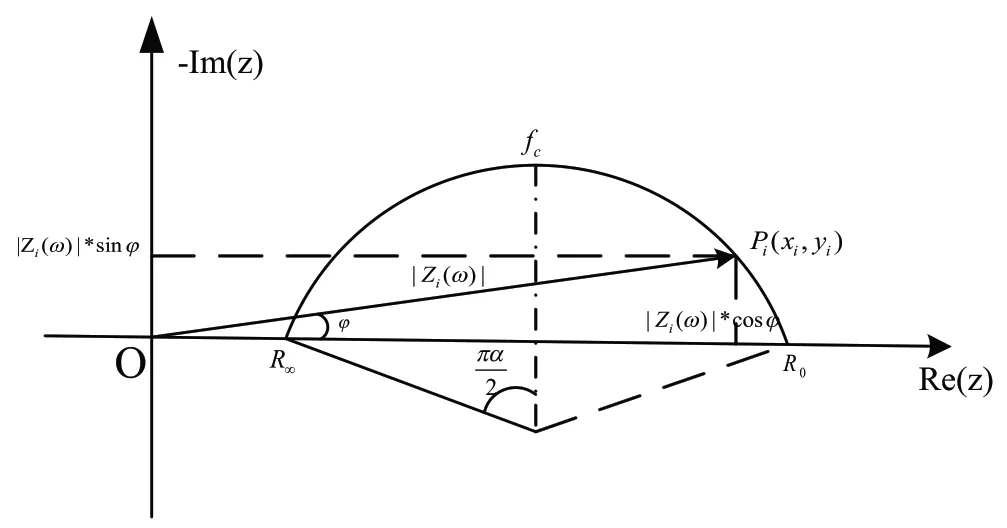
图2 生物组织细胞Cole-Cole圆弧Fig.2 Cole-Cole arc of biological tissue cells

其中，(x0,y0)为Cole-Cole圆弧的圆心，r0为半径。

根据式（1），弛豫时间常数τ表示为：

其中，Zi(ωi)表示fi激励频率下Cole-Cole圆弧轨迹上对应的复阻抗，且ωi= 2πfi。

将式（2）～（5）代入式（6）中，并化简：

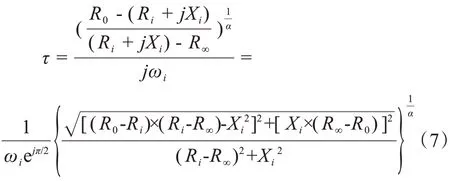
由于τ表示弛豫时间，为实数，因此：

为了确保测量精度，实际操作中采用多个数据点的平均值作为最终参数值：

综上所述，Cole-Cole 参数的提取流程如图3所示，可分为以下几个阶段：首先，根据阻抗数据拟合Cole-Cole 圆弧，得到圆心坐标和半径；接着，分析Cole-Cole 圆弧的几何关系，求解参数R0、R∞和α；最后，求解弛豫时间τ。

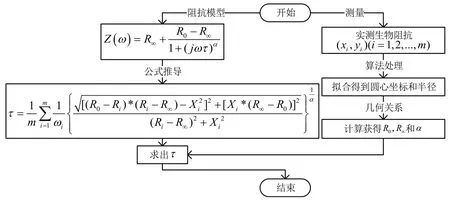
图3 Cole-Cole参数提取流程图Fig.3 Flowchart of Cole-Cole parameter extraction

1.2 自适应免疫-最小一乘算法

为了提高Cole-Cole 参数的提取精度，本文提出一种用于Cole-Cole 参数提取的自适应免疫-最小一乘算法，即AIA-LAD 算法。该算法一方面采用最小一乘法进行拟合，增强鲁棒性能；另一方面利用自适应免疫算法进行迭代，提高寻优能力。其中，自适应免疫算法是在传统免疫算法的基础上，借鉴遗传算法中精英保留的思想增设了记忆单元，并设计了适用于Cole-Cole 参数提取的抗体亲和度评价算子、抗体激励度算子、自适应变异算子和自适应克隆抑制算子。

（1）基于最小一乘法的抗体亲和度评价算子

采用最小一乘法拟合Cole-Cole圆弧的核心思想是使各阻抗点与拟合所得的Cole-Cole圆弧对应点的径向误差和最小：

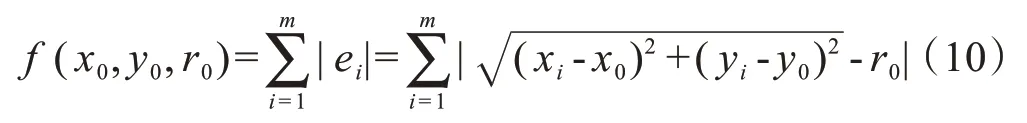
其中，(x0,y0)、r0为抗体解，分别表示拟合Cole-Cole 圆弧的圆心坐标与半径。因此，通过确定最小径向误差和即可获得Cole-Cole 参数，但由于存在绝对值运算，造成参数的直接求解较为困难，且最小一乘法可看作一种无约束多元非线性优化问题，因此本文结合最小一乘与迭代寻优算法进行Cole-Cole参数的求解，并设计了新的抗体亲和度评价算子：

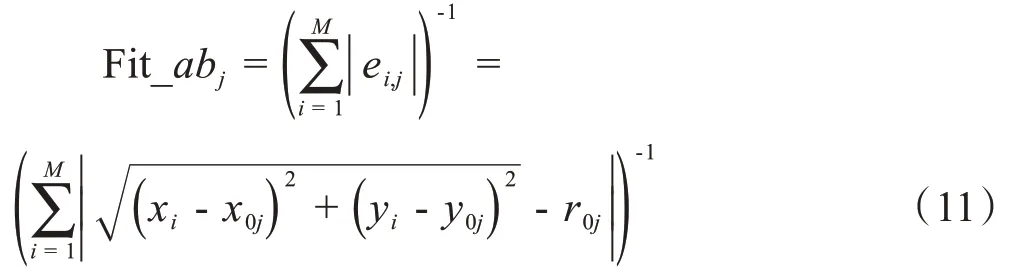
其中，Fit_abj表示第j组抗体解的亲和度，ei,j表示第i组阻抗值(xi,yi)与第j组抗体解的径向误差，误差越小、亲和度越高，(x0j,y0j)和r0j分别表示第j组解中圆弧的圆心和半径。

（2）抗体激励度算子

第j组抗体解与第k组抗体解的距离表示为：

其中，abj,t和abk,t分别为第j组与第k组抗体解的第t维数值，L为抗体编码的总维数。

抗体间的相似度可通过设定相似度阈值δs来区别：

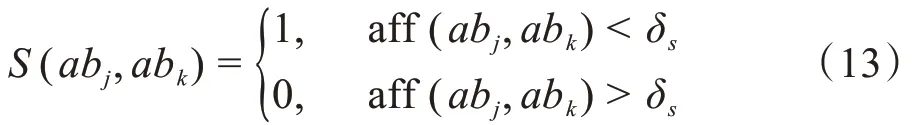
若两个抗体解的距离小于δs，则抗体间相似度S(abj,abk)= 1；反之，S(abj,abk)= 0。

根据抗体间的相似度，将抗体浓度Den_abj表示为：

进而得到抗体激励度算子

其中，η、ϕ为计算系数。

（3）自适应变异算子

为了提高算法前期抗体种群的多样性，并改善后期局部寻优能力，本算法设计如下自适应变异算子：

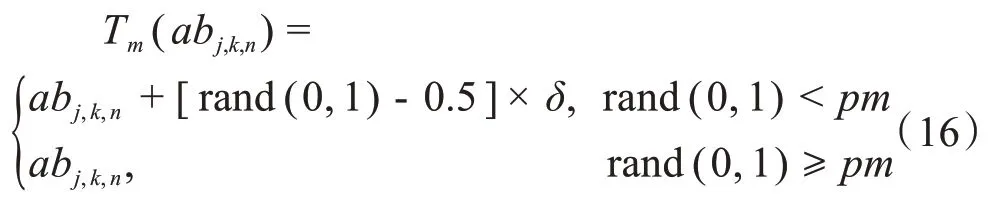
其中，abj,k,n表示abj第n组克隆抗体的第k维数值，rand(0,1)可产生区间(0,1)内的随机数，δ为偏移邻域内的随机数，pm为变异概率。该算子能自适应地改变抗体变异的偏移邻域大小与迭代过程中的变异概率。

抗体权重亲和度fg定义为：

其中，fbest,g、favg,g分别表示第g代抗体种群的最佳亲和度与平均亲和度。α、β均为计算系数，且α+β= 1。

为了更好地衡量抗体的收敛程度，将收敛因子λ定义为：

λ越小表示抗体越集中。可通过实时调节λ改变变异个体的偏移邻域Δ：

其中，ζ为计算系数，δ0_min、δ0_max分别表示邻域取值的下限和上限。

同时，将自适应变异概率pm定义为：

其中，PM表示变异率的初始值，g、G分别表示当前迭代次数与最大迭代次数，φ表示变异率衰减因子。

（4）自适应克隆抑制算子

AIA-LAD 算法通过设计自适应克隆抑制算子，保留了抗体种群的多样性，同时提高了算法的寻优速度，克隆抑制算子可表示为：

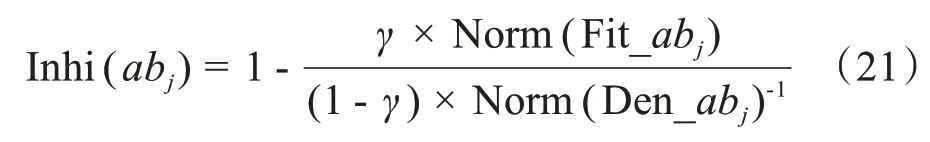
其中，γ表示适应度和浓度的权重因子，Norm(Fit_abj)、Norm(Den_abj)分别表示抗体abj适应度归一化与浓度归一化后的值。由式（21）可知，适应度越高、浓度越小的抗体保存至下一代的概率越大。因此，本算法不仅能保留高适应度抗体，而且可以提高抗体种群的多样性，进而使算法性能得到优化。

AIA-LAD 算法通过增设记忆单元存储每一代抗体种群中的优秀个体，并在每次迭代后自动更新该单元，从而提高算法的全局收敛速度。本算法流程如图4所示。

图4 AIA-LAD算法流程图Fig.4 Flowchart AIA-LAD algorithm

综上所述，AIA-LAD 算法提取Cole-Cole 参数的具体实现过程如下：（1）获取阻抗数据，初始化算法参数，并生成初代抗体种群；（2）根据最小一乘原理设置算法抗体亲和度评价算子；（3）计算每个抗体的抗体亲和度；（4）更新记忆单元中存放的抗体，并判断是否满足终止条件。若满足，执行（8），否则执行（5）；（5）计算抗体浓度与抗体激励度；（6）执行自适应免疫操作，包括免疫选择、克隆、自适应变异、自适应克隆抑制，生成子代抗体种群；（7）从子代抗体种群中筛选优秀抗体，结合记忆单元中的抗体形成新种群，并执行（3）；（8）输出亲和度最高的抗体所表示的Cole-Cole 圆弧的圆心和半径；（9）计算得到Cole-Cole参数R∞、R0、α和τ（或fc）。

2 实验验证

2.1 仿真数据集

本文通过参考文献［14-15］中阻抗数据集的设计方式建立仿真数据集。首先，设定Cole-Cole参数标准值：R0=150 Ω，R∞=50 Ω，α=0.8，τ=3.0×10-6，计算得到特征频率fc=53.0516 kHz；其次，在频率范围1 kHz～1 MHz内均匀选取呈对数分布的32个频率点；最后，根据Cole-Cole 方程生成各频率点对应的阻抗数据。标准阻抗数据均匀分布在圆心为（100，-16.246 0），半径为52.573 1的Cole-Cole圆弧上，同时，添加3种形式的噪声组合生成3组实验数据集，具体描述如下：

第1组数据集D1仅含奇异点噪声，即在标准数据集的第13 个和第25 个频率点处增加30%的径向误差，其余数据不变。

其中，xφ、yφ分别为标准阻抗数据的实部与虚部，xφ'、yφ'分别为添加噪声后阻抗数据的实部与虚部，θφ表示频率为fφ时径向与水平轴之间的夹角，θφ=arccos((xφ-x0)/r0)。

第2组数据集D2仅含随机噪声，即在标准数据集的16个偶频率点处(f2,f4,…,f32)分别增加-10%～10%的径向误差，其余数据不变。

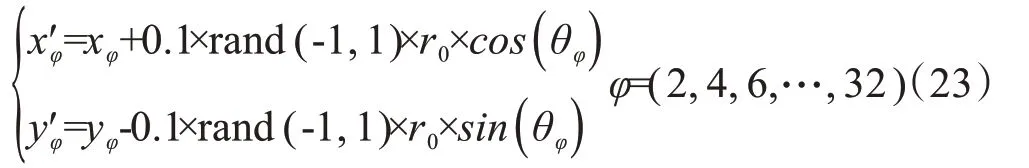
第3组数据集D3同时包含奇异点噪声和随机噪声，即在标准数据集的第13个和第25个频率点处增加30%的径向误差，并在16个偶频率点处（f2,f4,…,f32）分别增加-10%～10%的径向误差，其余数据不变。

2.2 实验结果

本文为了验证AIA-LAD 算法提取Cole-Cole 参数的优越性，将其与BFGS-LS、BFGS-LAD 和BFO-LAD 算法进行对比。本实验主要从拟合精度、耗时长短和初值依赖性3个方面展开讨论，每组实验各进行50次。

为了客观地比较4种算法的性能，本文设置了相同的目标参数(x0,y0,r0)的迭代初值：

其他初值分别设为：最大迭代次数50，种群大小20；根据多次实验结果，当η= 2，ϕ= 1，α= 0.3，β= 0.7，ζ= 2，PM= 0.8，φ= 0.5时算法结果最优。

（1）基于数据集D1，图5a～图5d分别对应4种算法对Cole-Cole 圆弧的拟合结果。图中红色实线表示标准Cole-Cole 圆弧，蓝色虚线表示拟合Cole-Cole圆弧，蓝色点为阻抗数据点。通过对比图中圆弧的重合程度，可知BFGS-LS算法拟合精度最低，其他3种算法拟合效果较好。本文选择相对误差作为算法提取精度的评价指标。表1列出了4种算法提取的Cole-Cole参数R0、R∞、α和fc及其相对误差eR0、eR∞、eα和efc。其中，AIA-LAD算法提取的各参数的相对误差均为0.00%。因此，该算法对奇异点噪声的敏感性较低，容错能力较强。

表1 数据集D1的4种算法的提取结果Tab.1 Extraction results obtained by 4 different kinds of algorithms for data set D1

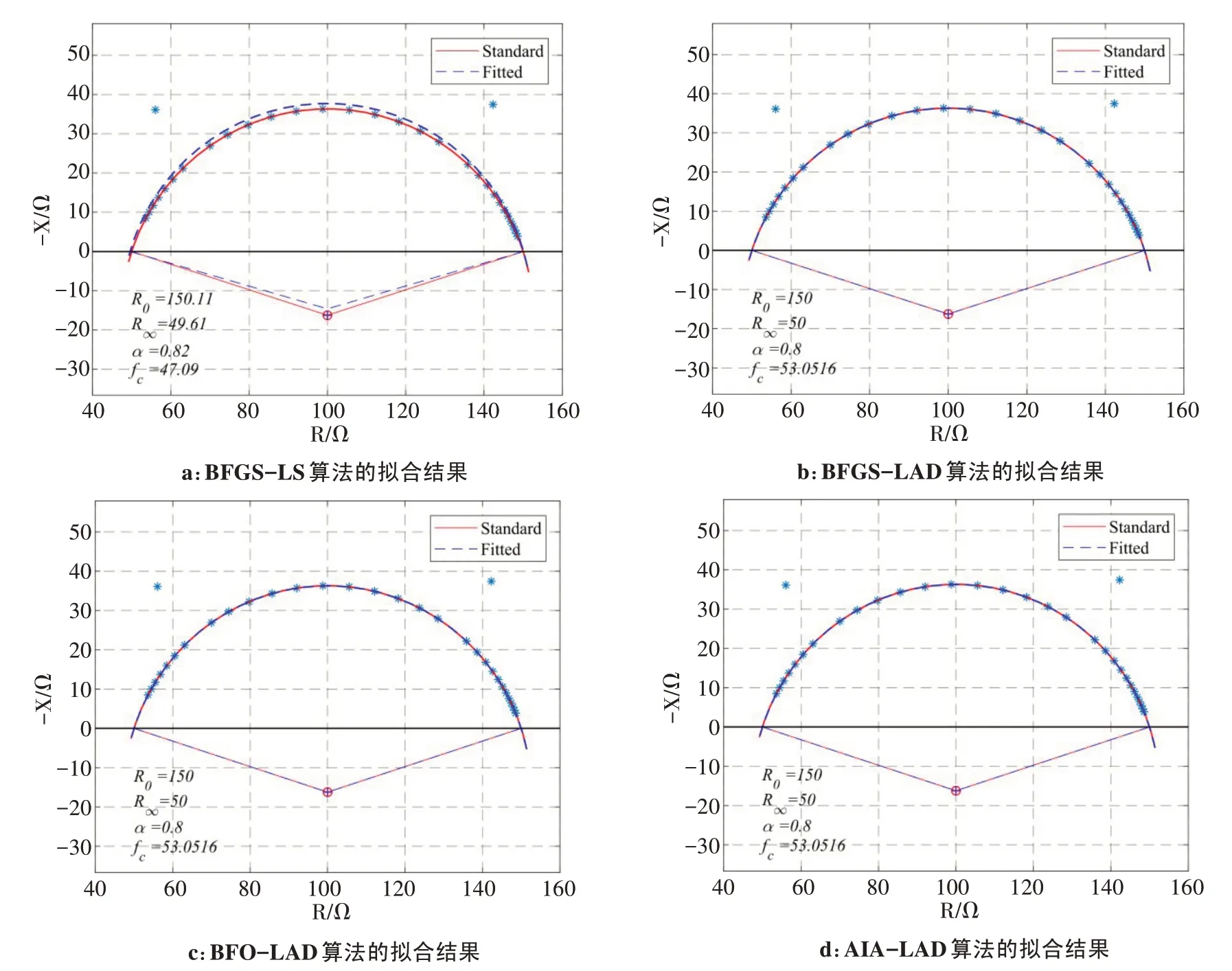
图5 数据集D1的4种算法拟合的Cole-Cole圆弧Fig.5 Cole-Cole arcs fitted by 4 different kinds of algorithms for data set D1

（2）数据集D2中含有随机噪声，因此本实验仅展示某次Cole-Cole 圆弧的拟合结果。对比分析图6中4种算法对Cole-Cole圆弧的拟合效果，显然BFGS-LS算法的拟合精度不如其他3种算法。表2显示4种算法提取的Cole-Cole 参数及其相对误差，表中数据均为50次实验结果的平均值。对比表中数据，4种算法的提取精度均受随机噪声的影响，其中，AIA-LAD算法提取结果的平均相对误差分别为0.26%、0.29%、0.27%、0.04%，均低于0.3%。

表2 数据集D2的4种算法的提取结果Tab.2 Extraction results obtained by 4 different kinds of algorithms for data set D2

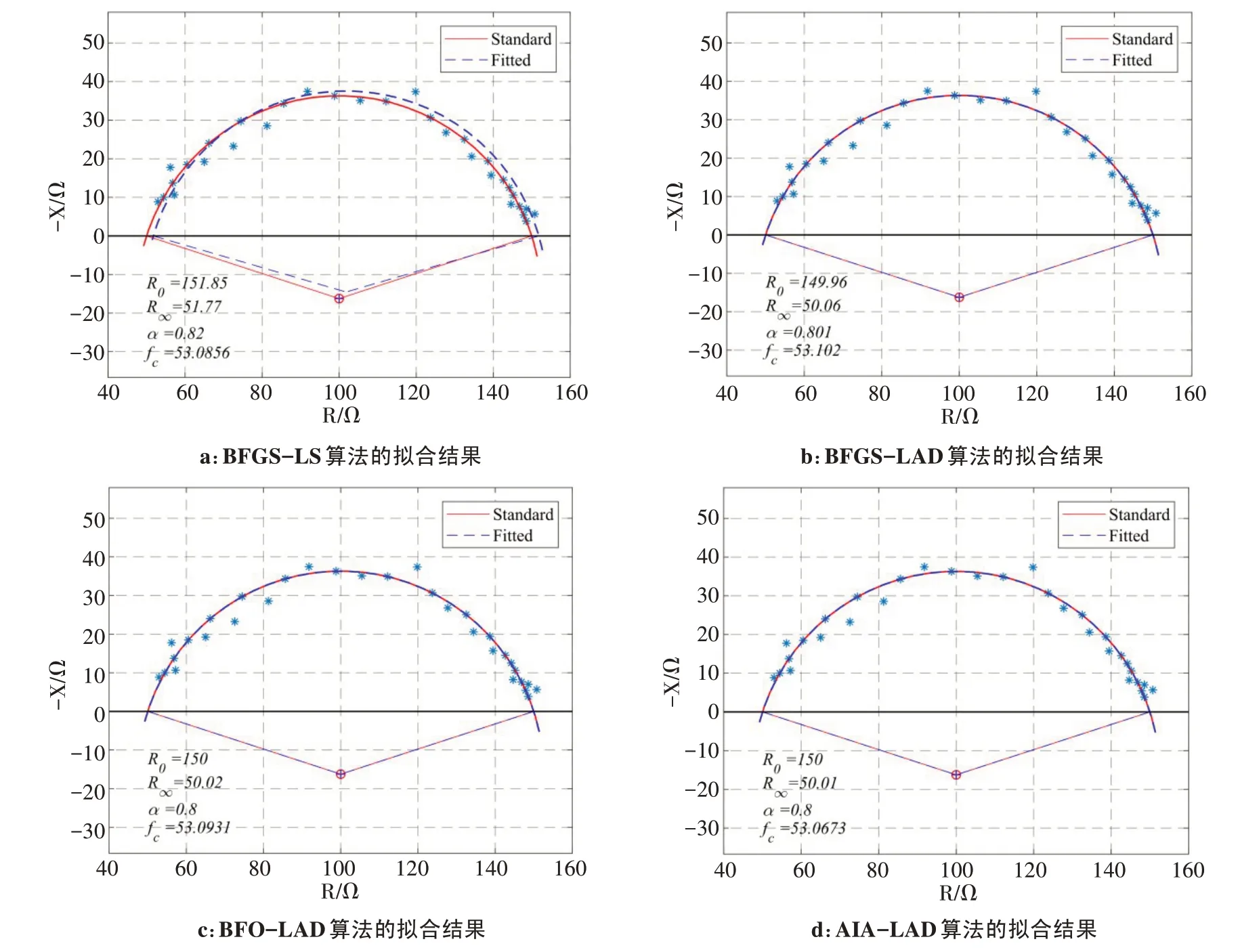
图6 数据集D2的4种算法拟合的Cole-Cole圆弧Fig.6 Cole-Cole arcs fitted by 4 different kinds of algorithm for data set D2

（3）图7为4 种算法对数据集D3的一个拟合结果，其中BFGS-LS 算法的拟合效果最差。表3数据均为50 次实验结果的平均值，AIA-LAD 算法提取的4 个特征参数的相对误差分别为0.43%、0.44%、0.69%、0.15%，均低于其他3种算法。因此，奇异点噪声与随机噪声同时存在时，AIA-LAD 算法的提取精度优于其他3种算法。

表3 数据集D3的4种算法的提取结果Tab.3 Extraction results obtained by 4 different kinds of algorithms for data set D3

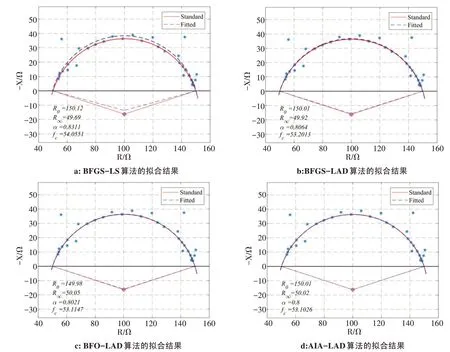
图7 数据集D3的4种算法拟合的Cole-Cole圆弧Fig.7 Cole-Cole arcs fitted by 4 different kinds of algorithms for data set D3

（4）利用MATLAB 2017b软件分别对4种算法提取Cole-Cole 参数进行代码实现，并对比耗时长短。电脑配置为Inter©CoreTMi7-9700 CPU@3.00 GHz，内存RAM 为16.0 GB，系统为64 位Win10 操作系统。实际环境中，奇异点噪声与随机噪声不可避免，因此本实验基于数据集D3对4 种算法提取参数的平均耗时进行了对比。BFGS-LS、BFGS-LAD、BFO-LAD、AIA-LAD 算法运行时间分别为15.26、15.03、9.02、6.57 s，可知AIA-LAD算法的耗时最短。

（5）另外，迭代初值也是影响算法提取精度的一个重要因素［13］。本实验基于数据集D3，通过设计一组较差的初值，评估AIA-LAD算法对初值的依赖性。其中，目标参数(x0,y0,r0)的迭代初值均设为200。根据表4中50次实验的平均结果可知，AIA-LAD算法在初值较差的情况下，依然能准确地提取Cole-Cole参数，提取得到的4个特征参数R0、R∞、α、fc的相对误差分别为0.51%、0.47%、0.45%、0.22%，均低于其他3 种算法，可知AIA-LAD 算法对初值设定的依赖性较弱。

表4 初值较差时数据集D3的4种算法的拟合结果Tab.4 Fitting results obtained by 4 different kinds of algorithms for data set D3 when the initial value is poor

根据所设计的多组对比实验结果显示，相较于其他3 种算法，AIA-LAD 算法在Cole-Cole 参数的提取过程中，拟合精度较高、耗时最短、初值依赖性最弱，且对噪声不敏感。

3 结论

本文为Cole-Cole参数的提取提供了一种新方法。该方法在传统免疫算法的基础上，设计自适应策略并引入记忆单元结构，同时，结合最小一乘法形成了一种结构简单、鲁棒性强的AIA-LAD算法。其中，自适应策略具体包括适用于Cole-Cole参数提取的抗体亲和度评价算子、抗体激励度算子、自适应变异算子和自适应克隆抑制算子。为了验证AIA-LAD算法提取Cole-Cole参数的有效性与优越性，本文通过在标准生物阻抗数据集的基础上增加奇异点噪声与随机噪声，形成3种不同的数据集，采用AIA-LAD、BFGS-LS、BFGS-LAD和BFO-LAD算法分别拟合Cole-Cole圆弧，并提取Cole-Cole参数，根据所设计的评价指标对4种算法的提取结果做出判断。同时，本文还对比分析了AIA-LAD算法提取Cole-Cole参数的耗时长短及对初值的依赖性。实验结果表明，AIA-LAD算法在含有噪声的生物阻抗数据集下有较高的拟合精度、较快的运行速度，且对初值的依赖性不高。因此，AIA-LAD算法的应用能够快速、有效地解决Cole-Cole参数的提取问题，降低算法对初值的依赖性。