BP网络在麻醉深度监测算法上的应用

顾家军，叶继伦，崔钰涵，陈谨，陈玲玲

1.深圳技术大学健康与环境工程学院，广东深圳518118；2.深圳大学医学部生物医学工程学院，广东深圳518060；3.广东省生物医学信号检测与超声成像重点实验室，广东深圳518060

前言

麻醉是现代医学临床手术中必不可少的关键环节，麻醉是由药物或其他方法产生的一种中枢神经和周围神经系统的可逆性功能抑制。麻醉过程中错误的麻醉药物剂量可能会导致病人麻醉过浅或过深［1］。如果病人接受不足的麻醉药剂量可能会在手术中出现知晓，引发大量的术后后遗症；过度麻醉药剂量会导致恢复时间延长，对病人的脑部产生有害影响，严重时将危及患者生命［2］。目前麻醉深度监测用主观方式通过观察病人受药物、手术刺激、原发疾病等影响较大的体征如呼吸、循环、眼、皮肤、消化道、骨骼肌张力等来判断；也可通过客观方式借助监护仪，对患者某些生命体征等进行监测，并给出定量的评价指数。客观方式易于了解当前患者的麻醉状态，对医生专业要求大大降低。脑电图信号具有反映意识活动的优势及无创性特点，是目前检测麻醉深度中最有潜力的方法之一［3-4］。目前基于脑电信号的检测方法主要有BIS（Bispectral Index）、Narcotrend、熵指数、听觉诱发电位等［5-6］。

1 脑电数据预处理

1.1 滤波

在手术室等场所，脑电信号易受高频电刀等设备所带来的脉冲干扰［7］。自适应阈值法是在阈值法的基础上，通过不断调整阈值以适应整个信号的变化，能够较好地克服因偶然因素引起的脉冲干扰。自适应阈值法首先将EEG 信号以每段含有0.5 s的数据进行分段。并计算一段数据的方差值，将该方差值乘以比例系数作为下一段数据的阈值，当下一段数据的方差小于阈值时，保留数据，同时修改阈值，否则删除这段数据。

脑电信号是低频信号，信号频段一般为0.5～35.0 Hz［8］。根据脑电信号的特点，通过设计相应的低通滤波器可以滤除高频噪声信号，保留有效的脑电信号。采用了4 阶47 Hz 的巴特沃斯低通滤波器，在保留脑电信号低频有效信号的基础上，滤除高频干扰信号。因脑电信号采集过程中易受到50 Hz 工频信号的干扰。通过采用4 阶50 Hz 的陷波器，来滤除工频信号的干扰。在脑电信号的采集过程中，还易受人体移动的干扰，产生基线漂移。基线漂移会使EEG 信号产生上下漂移，通过设计2 阶0.5 Hz 巴特沃斯滤波器的高通滤波器可以有效去除人体移动产生的干扰。脑电信号处理流程，如图1所示。

图1 脑电信号处理流程Fig.1 Electroencephalogram(EEG)signal processing

1.2 频域参数计算

当信号序列是有限长度时，周期图谱估计：

周期图法作为功率谱估计频率分辨率低，计算简单［9］。鉴于周期法的频谱性能不好，因此利用平均法对周期法进行方差特性改进，得到加权交叠平均法，即Welch 平均周期图法［10］。对L个具有相同均值μ和方差δ2的独立随机变量X1,X2…XL，新随机变量X=(X1+X2+…+XL)/L的均值为μ，方差减小了L倍。Welch 平均法将xN(n)分段，并且每一段的数据还可以有数据交叠，每段M点，段数为：

其中，lap 是交叠数据点数对每一段数据进行加窗w(n)，加汉明窗或者汉宁窗可以改善由于矩形窗边瓣较大而产生的谱失真。求其功率谱，记为:

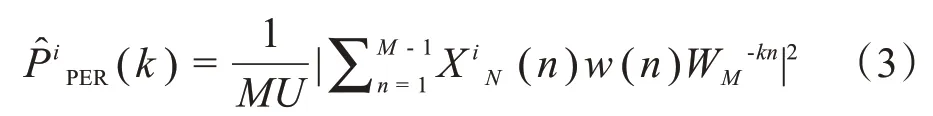
Welch 平均法具有数据交叠和段数增加的特点，计算量比较大。设P(k)为N点傅里叶变换的功率谱，求0～30 Hz波形总功率的计算公式为：

其中，fs是信号采样率，N是FFT 点数。转换为以dB为单位：TP = 10 × log10(Total_Power)。则各频带百分比［11］为：

EMG是频率为70～110 Hz的原始波形的功率。

BetaRatio 是30～47 Hz 与11～20 Hz 信号的功率比，患者处于轻中度镇静情况下与麻醉具有较好的趋势性［12-13］：

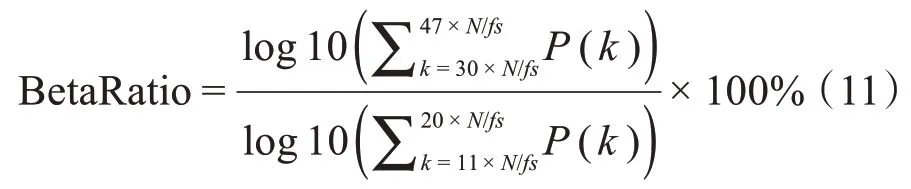
EMG 与BetaRatio 有较为类似的趋势图，为了剔除电刀等高频分量对BetaRatio 的影响，采用如下计算方式：

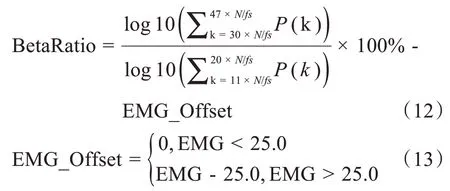
SEF定义为95%总功率处的频率参数值，其计算流程如图2所示，先计算95%总功率的值，再找出其所在频率位置［14-15］。

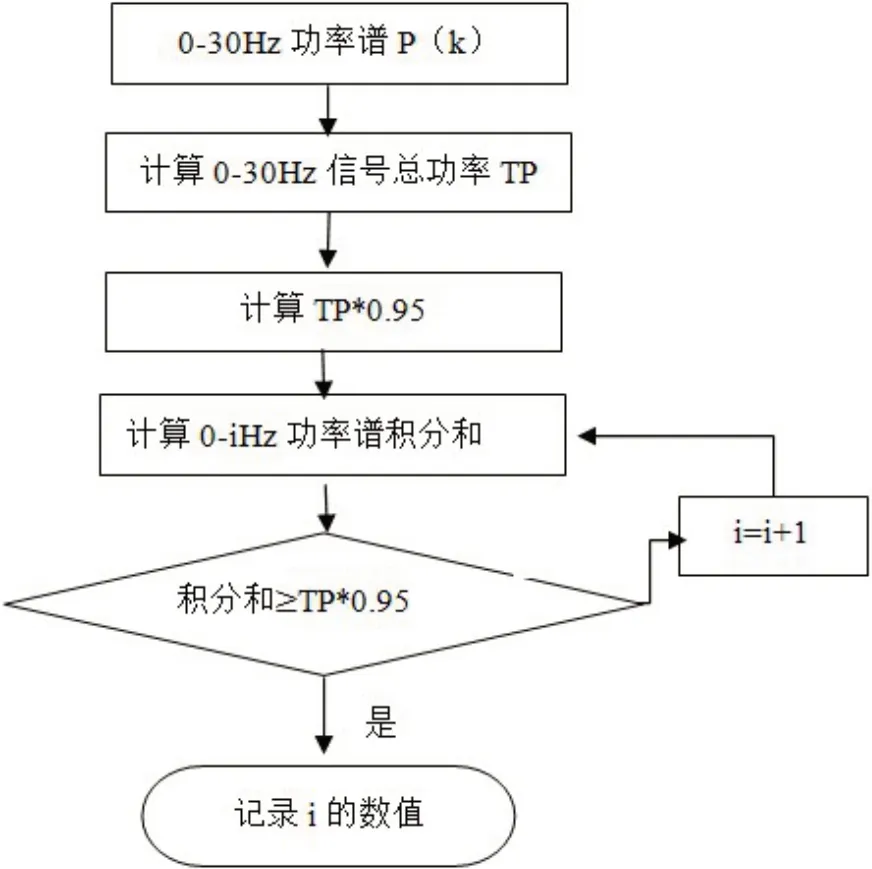
图2 SEF计算流程Fig.2 SEF calculation process

BSR 将60 s EEG 信号进行分段，每段长为0.5 s计算0.5 s EEG 数据段的标准差。根据标准差与阈值进行比较，判断该段信号是噪音还是抑制信号［16］。BSR计算流程如图3所示。

图3 BSR计算流程Fig.3 BSR calculation process

2 多层前馈（BP）网络拟合麻醉深度指数

2.1 BP学习算法

BP神经网络由输入层、隐含层和输出层组成［17］。工作信号的正向传播和误差信号的反向传播不断循环，使网络的输出和期望更加接近，直到网络的输出和期望的输出之间的误差足够小，或迭代的步骤达到预设限值。

2.2 样本的选择

（1）样本的质量：样本的质量主要考虑样本的分布和覆盖范围。本文选择BIS值作为训练的目标值，它是一个表示麻醉深度0～100的无量纲常数，能充分考虑到0～100的各阶段的麻醉深度情况［18-19］。

（2）样本的数量：训练样本太少，不足以表达全部规律，并且网络的准确度不够，泛化能力差。要求泛化结果的精度较高，则样本量要多，并且越多越好，但如果存在太多相似的样本，会增加网络的训练时间，导致拟合精度的下降。在确定网络的样本量时，可以适当牺牲网络的训练时间，以保证足够的网络准确度和泛化能力。对于麻醉深度指数的拟合，在保证足够多样本量的前提下，采用的训练样本数据基本可以覆盖BIS 指数在20～100 的全部过程。网络的输入样本包括SEF、BetaRatio以及BSR［20］。

2.3 BP网络的构建

BP网络结构的构建，主要包括BP网络层数和隐藏层神经节点的确定以及输入输出神经节点的设计。

2.3.1 BP 隐含层数的确定BP 网络的隐含层理论上可以无限大，但是隐含层如果过大，一方面会增加网络的复杂性，另一方面会导致“过拟合”现象。Hecht-Nielsen 证明了当各节点具有不同的门限时，对于在闭区域内的一个连续函数都可以用一个隐含层的网络来逼近，所以一个三层的BP 神经网络可以完成任意的n维到m维的映射。

2.3.2 BP 隐含节点数的确定隐藏层节点数过少，则训练的效果差，达不到训练的精度要求，降低网络的预测能力，即“欠拟合”。隐藏层节节点数太多，会导致“过拟合”现象。为了找到合适的隐藏层节节点数，先采用一个较小的隐藏层节点数训练网络，若达不到足够的精度，逐渐增大隐藏层节节点数，然后再重新训练网络。如表1所示，不同的隐含层节点数对网络的泛化能力的影响不大。主要有两个原因：一是为了提高网络的泛化能力，上述训练过程中使用了检查泛化能力的validation，设定max-failure 次数以后，如果训练以后参数值使得validation 的预测误差连续上升超过预设值次数，就停止训练。二是采用比较简单的麻醉深度指数函数，通过三层BP网络，利用较少的节点数足以拟合出该函数。因此为了减小网络结构，采用较小的网络，设置隐藏层节点数为5。

表1 隐含层节点数对网络泛化能力的影响Tab.1 Effects of the number of hidden layer nodes on network generalization ability

2.3.3 BP 网络输入输出节点的选择输入节点数取决于数据源的维数和输入特征向量的维数。麻醉深度指数是由SEF、BetaRatio 和BSR 3 个参数拟合而成，网络输入节点数设置为3个。网络的输出只有一个参数，即麻醉深度评价值，是一个0～100 的无量纲的值，所以网络的输出层节点数设置为1。

2.3.4 网络激励函数的选择本文主要考虑的是不同激励函数对网络的泛化能力是否有影响。如表2所示，选择不同的激励函数，网络泛化能力的变化不大。由于BIS函数是一个线性函数，因此本文最终选择的是线性激励函数PURELINE。

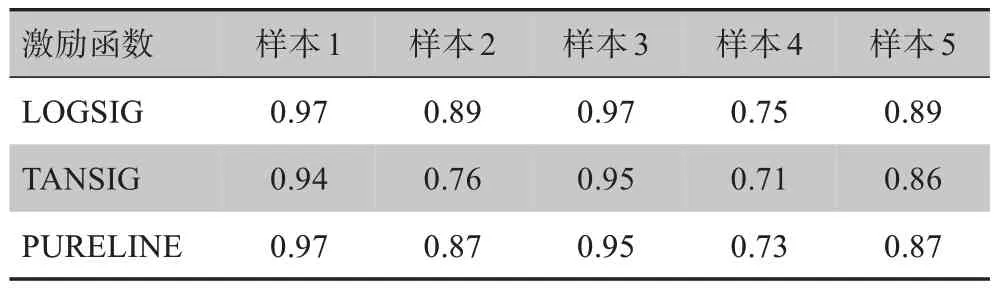
表2 激励函数对函数泛化能力的影响Tab.2 Effects of excitation function on function generalization ability

2.3.5 不同学习函数对网络泛化能力的影响BP 神经网络不同的训练算法对网络的泛化能力、收敛速率、稳定性都有很大的影响。对于一个给定的问题，采用哪种训练方法的训练速度最快，这是很难预知的。本文主要考虑的是不同训练函数对网络泛化能力的影响。不同的训练函数，拟合的BIS 值和BIS 值之间的相关系数r值不同。如果某一训练函数的各个验证样本得到的r值，整体大于其他训练函数得到的r值，则说明用该函数训练得到的网络泛化能力强。如表3所示，除了traingd 梯度下降法和taingdm动量BP 算法这两种算法的效果明显不好，其他算法训练出来的网络泛化能力差别不大。虽然可变学习率的算法收敛速度较慢，但考虑到在某些特定的情况下，算法的收敛速度太快，可能得到的结果还达不到所要求的目标时训练就提前结束了，错过使误差最小的点。因此最终本文决定采用学习率可变的动量BP 算法Traingdx，该算法是BP 网络中最常用的训练算法之一，且算法简单。

表3 训练函数对拟合值的相关系数的影响Tab.3 Effects of training functions on the correlation coefficient of the fitted values

3 验证分析

通过上述研究，本文采用的是3 层BP 网络，该网络有3 个输入节点，分别是SEF、BetaRatio 以及BSR。网络有1 个输出节点。隐含层节点数是5 个，输入层到隐含层的激励函数为非线性函数LOGSIG，隐含层到输出层的激励函数为线性函数PURELINE。网络的学习函数采用改进梯度下降算法和学习率可变的动量BP 算法，同时为了提高网络的泛化能力采用早停法，网络的误差函数选用的是均方误差函数。如图4所示，拟合结果普遍准确度约0.9，标准偏差约5，相关系数r值约0.9，并且拟合结果在0～100 整体呈线性分布。其中个别样本的拟合结果不太理想的，一是SEF、BetaRatio 以及BSR 的突变导致的拟合值的突变；二是输入端节点过少。

图4 验证样本拟合效果分析Fig.4 Analysis of fitting effect on validation samples

4 结论

BP 神经网络拟合麻醉深度值与BIS 值相比较，能够达到一个比较高的精确度。但是拟合的BIS 值存在突变，这种突变是由于输入端的计算参数的突变导致的，同时输入端节点较少，与网络的结构无关。从根本上消除这种同突变，必须从网络层的输入参数的计算及丰富输入端参数节点入手。本文的研究表明，通过BP 神经网络的输出值表征麻醉深度具有较好的应用效果。