基于灰色预测模型的EMD 端点效应抑制方法

钱 欢， 蒋 沅， 王海涛

（1. 南昌航空大学 信息工程学院，南昌 330063； 2. 中建一局集团第二建筑有限公司，北京 102600）

引 言

现实生活中的信号绝大部分都是非线性、非平稳信号，处理这类信号最行之有效的方法是时频分析法，常用的传统时频分析法如Fourier 变换、小波变换、Gabor 变换和Winger-Ville 分布在处理信号时，通常认为信号是线性的、平稳的。为了解决上述方法的局限性，Norden E. Huan 等[1]创造性地提出了经验模态分解法，经验模态分解法是一种基于原始信号自身特征量进行分解的自适应时频信号处理方法。因而广泛应用于结构损伤检测、机械故障诊断[2]和滤波降噪等领域[3]。在进行EMD分解时，采用精度较高的3 次样条插值法对信号的极值点进行拟合求取信号的上、下包络线。由于极值点分布不均以及无法确定信号端点处是否为极大值点或极小值点，产生了非均匀点拟合的现象，导致拟合的包络线在信号的端点处发生形变，产生“过冲”和“欠冲”的现象[4]，使得包络线无法将整个信号完全“包住”，最终导致所求包络线的均值误差较大。而第一个IMF 是原始信号减去包络线均值后再进行迭代处理所得，由于包络线均值存在误差导致误差最终传递到IMF 上。在接下来每次分解产生的新的IMF 时误差不断累积加大，最终导致得到的各个固有模态分量不能准确反映原始信号的组成成分，分解的完备性遭到破坏。为了有效抑制端点效应造成的失真问题，总结国内外学者的研究方法主要可以分为以下几类：1）首先是基于原始信号的波形特征进行处理，如黄大吉的镜像闭合延拓法[5]，通过设置镜面把原始信号延拓成一个没有端点的闭合信号环，然而该方法对于信号的对称性要求较高，适用范围有限；2）其次是基于数学预测模型的方法，通过使用特殊的数学模型对原始信号两端进行延拓，如程军圣的自回归滑动平均模型[6]，该方法对于平稳信号和常见的非平稳信号处理效果良好，但是对于复杂的非平稳信号处理精度不高；3）最后是基于神经网络的方法，郝如江使用支持向量机[7]对数据进行预测延拓，但是该方法也存在核函数和最优参数选择的问题。以上诸多方法对于抑制端点效应起到了一定的作用，但由于方法过于单一，在处理复杂信号和短时序信号等特殊信号[8-10]时效果不够理想。对此本文提出一种基于灰色预测和加窗函数的改进处理方法，针对短时序、小样本信号，通过引入灰色均值GM(1,1)预测模型对短时序信号进行精确预测，在原始信号两端各延拓出若干极值点，然而即使这样我们依然无法准确判断信号的端点情况，因此还需结合矩形窗和汉宁窗这两种窗函数，即一方面通过矩形窗强化中部原始数据，保护原始信号不失真，另一方面对两端的延拓部分施加汉宁窗让信号平缓过渡，使端点处的值趋于零，拟合的包络线最终也收敛于端点处，因此信号的端点情况得到确认，使包络拟合时不再出现形变发散的问题，从而实现抑制端点效应的目的。

1 EMD 及其端点效应

1.1 EMD 分解

NASA 科学家Norden E. Huan[1]早期在处理海洋波信号时假设多分量信号都是由一系列基于时间特征尺度的固有模态分量相互叠加而成，将非线性、非平稳信号按局部频率由高到底筛分出固有模态分量和一个单调的趋势项分量，实质上是对信号中不同波动特性的分量进行分离，将各个固有模态分量经希尔伯特变换得到解析信号和瞬时频率，同时Huang[1]论证了EMD 满足完备性、正交性和调制性等特点。其中满足IMF 分量的2 个条件如下：1)极值点数和过零点数之差等于0 或者1；2)极大值和极小值所构成包络线的均值为0。EMD 算法实现过程如下：

(1)对原始信号x(t)的极值点进行3 次样条插值拟合上下包络线a(t) 和b(t)， 包络线均值记作m1(t)：

(2)从原始信号中去除低频分量m1(t)，剩余的记作h1(t)：

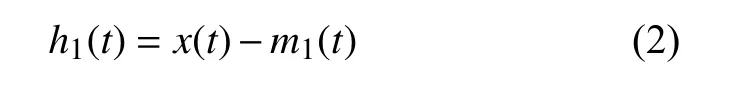
(3)判断h1(t)是否满足成为IMF 的条件，如果满足条件则认定h1(t)就是第一个IMF，并让c1(t)=h1(t)。

(4)如果不满足条件则将h1(t)作 为新的x(t)重复上述过程，在迭代k次后满足条件后成为IMF1，记作h1,k(t)并 且c1(t)=h1,k(t)，迭代的终止是筛选门限S D∈[0.2,0.3]， 门限S D计算公式如下：

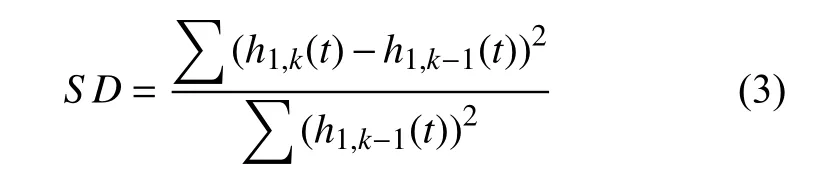
(5)令r1(t)=x(t)−c1(t)， 把r1(t)作 为新的x(t)重复上述过程，得到剩余的IMF，其中残余分量记作rn(t) ， 当rn(t)为常数或单调函数时，EMD 过程结束，x(t)如式（4）所示：

1.2 端点效应

在EMD 分解的迭代过程中，需要多次使用3 次样条插值对信号 的极大值和极小值点进行拟合求取上、下包络线，受制于无法准确判定端点是否为极值点的问题，导致拟合的包络线在端点处发生偏移甚至发散，进而导致包络线均值失真，拟合的上包络线无法将原始信号完全包住，导致第一个IMF 分量和原始信号的高频分量之间存在较大误差，随着EMD 迭代分解的不断进行，使得端点出现的失真问题，不断向中间数据进行传导，导致整个数据序列都受到“污染”，最终结果是所得各IMF 分量无法准确表征原始信号。

2 灰色预测模型

当前的预测方法在样本较少时的预测误差都比较大，灰色预测模型通过关联分析判断系统内部动态发展趋势，灰色生成关联性较强的数据序列，从而预测样本的发展趋势。灰色预测模型在不改变原有信号的基础上具有预测精度高、计算简单等优点，相较于ANN 预测，不需要大规模的训练，具有计算量小，耗时短的优点；相较于SVM 预测，不存在核函数选取和参数设定困难的问题。因而针对小数据、贫信号预测的灰色预测模型逐渐成为灰色系统领域研究的热点方向，其中基于灰色预测模型及其组合方法应用成果显著，如王守相等[11]运用灰色预测模型和神经网络组合算法实现光伏出力情况预测；如刘思峰等[12]提出基于灰色关联度和GM(1,1)灰色组合预测模型的GDP 预测。其中GM(1,1)模型是由单变量的一阶灰色微分方程构成的模型，能在不改变信号原有特性情况下对复杂的不确定性信号进行有效预测，并且该模型只需要4 个以上样本点便可以实现对数据的预测，对短时序的贫信号预测效果明显，GM(1,1)相较于其它灰色模型还具有计算简便适、适合实时预测等优势，灰色动态模型算法实现过程如下：

3 基于灰色预测的改进方法

3.1 加窗函数

窗函数也称计权函数，常见的窗函数有指数窗、矩形窗、海明窗和平顶窗等[13]。我们一方面希望原始信号加窗后所拟合的包络线更加贴合原始信号，降低包络线在端点处的发散程度；但另一方面在加窗后，原始信号的起始位置和结束位置的计权结果为零，导致原始信号两端出现幅值失真，因此为了降低加窗函数后对原始信号的影响，需要先对原始信号进行延拓，让加窗函数造成的失真发生在延拓部分同时也要保证原始信号本身所受影响最小。加窗函数从本质上来说是原始信号和计权函数相乘的[14]过程，为实现上述目标，本文将矩形窗和汉宁窗结合使用，对原始信号乘以一个计权权重为1 的矩形窗不改变原始信号，对两端的延拓部分加汉宁窗让延拓部分趋于0，这样拟合出的包络线会收敛端点处而不再发散，两种窗函数如式（15）和式（16）所示。

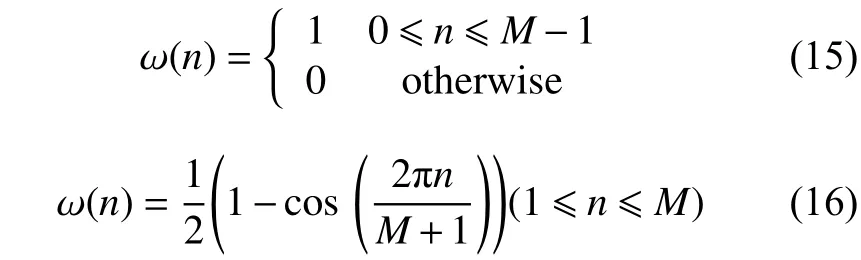
对原始信号建立GM(1,1)灰色动态预测模型，在原始信号两端延拓出两个以上极值点，再对延拓的信号加汉宁窗，对延拓的左端信号和窗函数的左上升沿做内积，右端信号和窗函数的右下降沿做内积，加窗后两端处值趋于零从而能拟合出更加平滑的包络线，对中部的原始信号部分和矩形窗在做内积，不改变原始信号特征，最后对处理后的数据进行EMD 分解，在分解后的IMF 分量中去舍弃掉延拓部分，剩下部分则是所求的真正IMF 分量。

3.2 算法的评价指标

分解处理后需对端点效应的抑制效果进行评价以此来证明本算法的有效性，本节使用均方根误差发和相似系数法两个指标来对分解效果进行量化分析。均方根误差法通过比较得到的各IMF 分量和原始信号对应组成分量之间的均方根误差[15]进行判断，均方根误差值越小，则说明IMF 在端点处的发散程度就越小，分解的效果就越好，均方根误差计算公式如下：

相似系数用于比较分解后各IMF 分量和原始信号对应组成分量之间的相似程度，相似度越高，表示分解的效果越好，相似系数计算公式如下：

4 实验分析

4.1 仿真信号分析

图1 对合成信号直接进行EMD 分解

所示，在分解结果的端点出现了发散现象存在明显的端点效应，并且随着分解的进行还出现了虚假分量IMF3，本文改进方法处理y(t)后如图2 所示，EMD分解结果如图3 所示，相较于直接进行EMD 的处理结果可以发现IMF 分量的端点效应得到有效抑制，而且虚假分量IMF3 也消失了。

图2 本文算法处理后的合成信号

图3 本文方法处理后的信号进行EMD 分解

分别将几种不同算法处理后得到的IMF1 和IMF2 与组成分量作比较（如图4a、图4b）。通过对比图可以看出经端点处理后得到的IMF 分量和未经处理得到的IMF 分量相比更接近原始信号分量，其中红色波形曲线和其它方法的波形曲线相比，和信号分量更加贴近。为了对比这几种方法对信号处理效果，分别采用相似系数法和均方根误差法量化评价分解结果，使用均方根误差法分别对IMF1 和x1(t)、 IMF2 和x2(t)求均方根误差以及计算IMF 分量和信号组成分量之间的相似系数。结果如表1 所示，结果也说明本文改进算法对EMD 过程中的端点效应有相对更好的抑制效果。

表1 IMF 分量与原始信号的均方根误差和相似系数

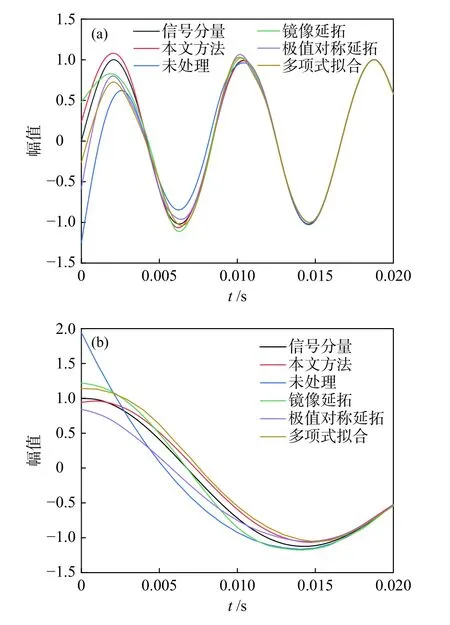
图4 各种算法处理后IMF1 和IMF2 的局部放大图

4.2 实测信号分析

本文采用美国西储大学的故障轴承振动加速度信号作为处理对象，数据由加速度传感器对驱动端的轴承SKF6025 进行采集，采样频率为12 KHz，由于数据量较大，使用的采样点数量为800 个。图5 所示直接进行EMD，图6 和图7 所示为采用本文改进方法，先在信号两端进行预测延拓和加窗处理后再进行EMD，处理后的所得IMF 分量的发散现象得到有效抑制，起到了抑制端点效应的目的。

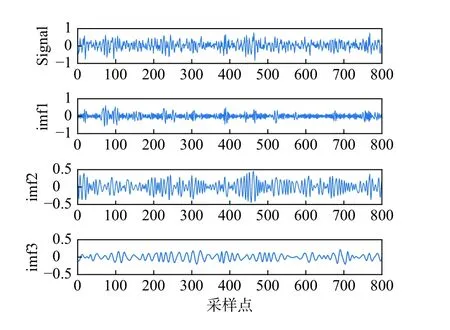
图5 振动信号直接进行EMD 分解的结果

图6 本文方法处理后的振动信号

图7 本文方法处理后进行EMD 分解的结果

5 结 论

1) 本文提出一种基于灰色预测模型和加窗函数相结合的改进处理方法，对原始信号加矩形窗保持信号不变，对两端延拓信号加汉宁窗抑制两端波形突变，使拟合的包络线能完全包络信号。

2) 文末通过信号分析对比改进方法处理前后端点的发散情况，以及使用均方根误差法量化评价相似性，发现该方法明显优于一般地EMD 分解，可以有效地抑制端点效应导致的失真问题。

3) 然而灰色预测模型在处理复杂信号时存在预测精度不够，对随机震荡序列预测效果不好等问题，还需要不断地优化和完善。